桂林2024年秋季期中联考高一数学试卷_2024-2025高一（7-7月题库）_2024年11月试卷_1115广西桂林2024-2025学年秋季期中高一联考

普通高中 2024 级高一年级联合调研检 数 学 （本试卷满分150分，考试时间120分钟） 注意事项： 1．答题前，务必将自己的姓名、班级、准考证号填写在答题卡规定的位置上。 2．答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦 干净后，再选涂其它答案标号。 3．答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。 4．所有题目必须在答题卡上作答，在试题卷上答题无效。 一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一个选 项是符合题目要求的。 1．设集合A{3,2,1}，B{x|3x„1}，则AB A．{x|3 x„1} B．{2，1} C．{3，2，1} D．{x|1„x„1} 4 2．已知命题 p:x0，x 4，则¬p为 x 4 4 A．x0，x 4 B．x„0，x 4 x x 4 4 C．x„0，x 4 D．x0，x 4 x x 1 3．函数 f(x) x2 4 的定义域为 x3 A．[2,) B．(,2][2,) C．(,2][2,3)(3,) D．[2,3)(3,) 4．已知函数 f(x)(k1)xk1是幂函数，则 f(2) A．8 B．4 C．2 D．1 5．下列函数中，既是奇函数，又在区间(0,)上是增函数的是 2 1 3x2 A．y|x| B．yx C．yx D．y x x x1 2 1 6．已知x0,y 0，且2x y 1，则  的最小值为 x y A．6 B．9 C．12 D．18 7．“空气质量指数(AQI)”是定量描述空气质量状况的无量纲指数．当AQI大于200时，表示空气 重度污染，不宜开展户外活动．某地某天0~24时的空气质量指数y随时间t变化的趋势由函数 10t290,0„t„12 y 描述，则该天适宜开展户外活动的时长至多为 56 t 24,12t„24 A．5小时 B．6小时 C．7小时 D．8小时 高一数学 第1 页 共4页 学习资料，无偿分享8．已知定义在R上的函数 f(x)x2 2tx1在(，1]上单调递减，且对任意的x ，x [0，t1]， 1 2 总有| f(x ) f(x )|„6，则实数t的取值范围是 1 2 A．[1, 2] B．[1，1] C．[ 6 ， 6] D．[1， 6] 二、多项选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合题目 要求。全部选对的得6分，部分选对的得部分分，有选错的得0分。 9．已知d c0ba，则 A．ac2bbc2a c c B．  a b C．ad bc 1 1 D．  a b 10．已知函数 f(x) x2 4|x|，则下列结论正确的是 A． f(x)在[2,)上单调递增 B．若t 3，则 f(t) f(t2) C．方程 f(x)1有2个解 D．若 f(a) f(b)1，则ab0 11．对于定义在R上的函数 f(x)，若 f(x1)1是奇函数， f(x1)是偶函数，且 f(x)在[1，2]上 单调递减，则 A． f(3)0 B． f(0) f(2) C． f(1) f(2) f(3) f(2023) f(2024)2024 D． f(x)在[4,5]上单调递减 三、填空题：本题共3小题，每小题5分，共15分。 12．已知定义在R上的奇函数 f(x)2x3x2m，则m______. 13．已知函数 f(x3)x2 4x6，则 f(x)=_________. 14．已知a、b、c均为实数且ab0，令函数 f(x)ax2 bxc ，若对∀x∈R，f(x) 0恒成立， b 则 的最大值为_________. abc 高一数学 第2 页 共4页 学习资料，无偿分享四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。 15．（13分）设集合A{x||x3|2}，B{x|1x2m1}． （1）当m1时，求AB； （2）若“xA”是“xB”的充分不必要条件，求实数m的取值范围． 16．（15分）已知函数 f(x) x2 (4k)x3k3，其中k∈R． （1）若 f(x)0的解集为(3,5)，求k； （2）求关于x的不等式 f(x)0的解集，其中k为常数. 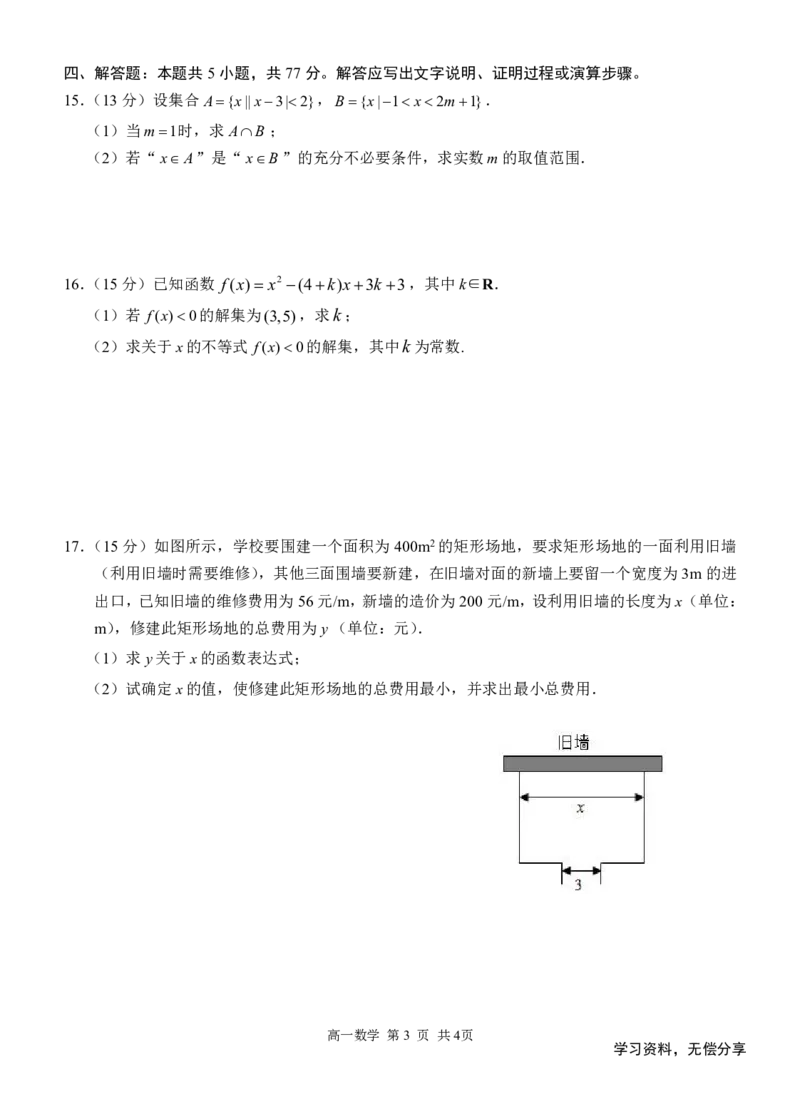17．（15分）如图所示，学校要围建一个面积为400m2的矩形场地，要求矩形场地的一面利用旧墙 （利用旧墙时需要维修），其他三面围墙要新建，在旧墙对面的新墙上要留一个宽度为3m的进 出口，已知旧墙的维修费用为56元/m，新墙的造价为200元/m，设利用旧墙的长度为x（单位： m），修建此矩形场地的总费用为y（单位：元）． （1）求y关于x的函数表达式； （2）试确定x的值，使修建此矩形场地的总费用最小，并求出最小总费用． 高一数学 第3 页 共4页 学习资料，无偿分享18．（17分）已知函数 f(x)满足对一切实数x ，x 都有 f(x x ) f(x ) f(x )2成立，且 f(1)0， 1 2 1 2 1 2 当x1时有 f(x)0． （1）求 f(0), f(2)； （2）判断并证明 f(x)在R上的单调性； （3）解不等式[f(x2  x)]2 4f(x2  x1)4＜0． 19．（17分）已知a、b、c均为正实数. （1）证明：abc 2ab  2bc ； abc 1 （2）证明  3 abc,并求 y2x (x＞2）的最小值； 3 (x2)2 1 1 1 （3）若abc1，求证：   2. a c2 1 b a2 1 c b2 1 高一数学 第4 页 共4页 学习资料，无偿分享