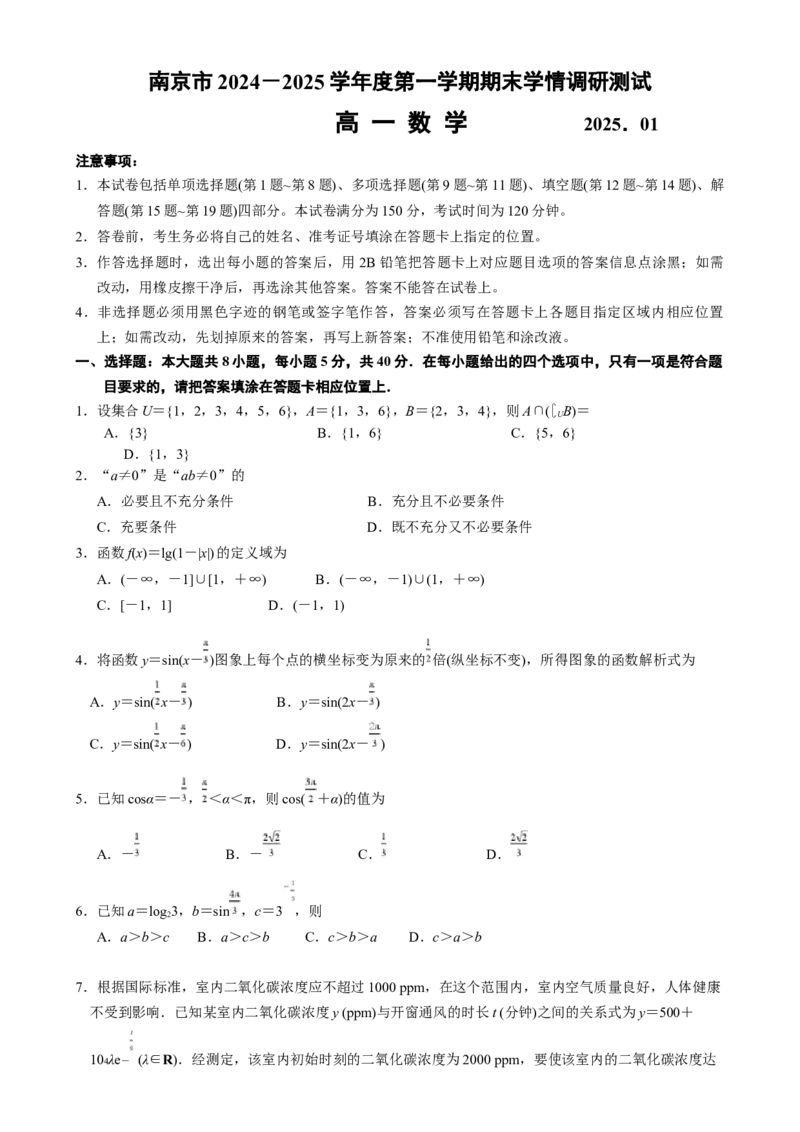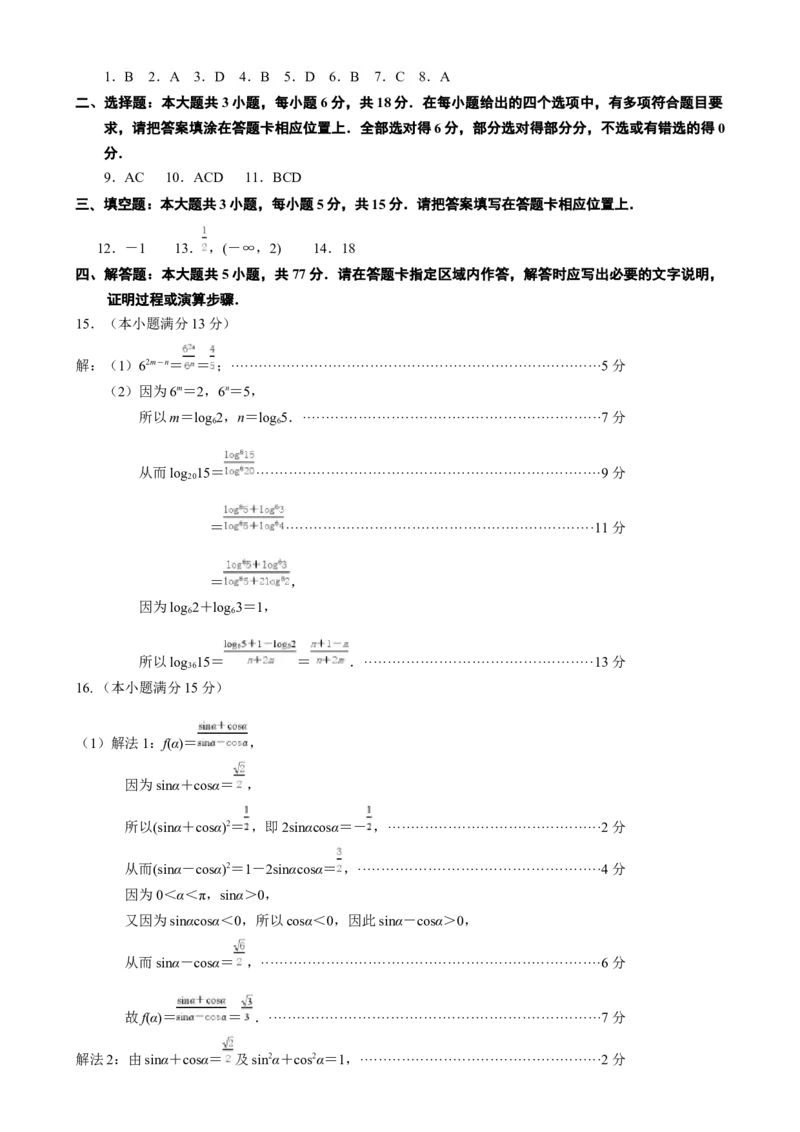文档内容
南京市 2024-2025 学年度第一学期期末学情调研测试
高 一 数 学
2025.01
注意事项:
1.本试卷包括单项选择题(第1题~第8题)、多项选择题(第9题~第11题)、填空题(第12题~第14题)、解
答题(第15题~第19题)四部分。本试卷满分为150分,考试时间为120分钟。
2.答卷前,考生务必将自己的姓名、准考证号填涂在答题卡上指定的位置。
3.作答选择题时,选出每小题的答案后,用 2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需
改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试卷上。
4.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡上各题目指定区域内相应位置
上;如需改动,先划掉原来的答案,再写上新答案;不准使用铅笔和涂改液。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题
目要求的,请把答案填涂在答题卡相应位置上.
1.设集合U={1,2,3,4,5,6},A={1,3,6},B={2,3,4},则A∩(∁ B)=
U
A.{3} B.{1,6} C.{5,6}
D.{1,3}
2.“a≠0”是“ab≠0”的
A.必要且不充分条件 B.充分且不必要条件
C.充要条件 D.既不充分又不必要条件
3.函数f(x)=lg(1-|x|)的定义域为
A.(-∞,-1]∪[1,+∞) B.(-∞,-1)∪(1,+∞)
C.[-1,1] D.(-1,1)
4.将函数y=sin(x- )图象上每个点的横坐标变为原来的 倍(纵坐标不变),所得图象的函数解析式为
A.y=sin( x- ) B.y=sin(2x- )
C.y=sin( x- ) D.y=sin(2x- )
5.已知cosα=- , <α<π,则cos( +α)的值为
A.- B.- C. D.
6.已知a=log 3,b=sin ,c=3 ,则
2
A.a>b>c B.a>c>b C.c>b>a D.c>a>b
7.根据国际标准,室内二氧化碳浓度应不超过1000 ppm,在这个范围内,室内空气质量良好,人体健康
不受到影响.已知某室内二氧化碳浓度y (ppm)与开窗通风的时长t (分钟)之间的关系式为y=500+
104λe- (λ∈R).经测定,该室内初始时刻的二氧化碳浓度为2000 ppm,要使该室内的二氧化碳浓度达到国际标准,则需要开窗通风的时长至少约为(参考数据:ln3≈1.099,ln5≈1.609)
A.6分钟 B.8分钟 C.10分钟 D.12分钟
8.若命题“x>0,(ax-1)(x2-2ax-1)≥0”是真命题,则实数a的取值集合为
A.{ } B.{ } C.{a|a≥ } D.{a|0<a≤ }
二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要
求,请把答案填涂在答题卡相应位置上.全部选对得6分,部分选对得部分分,不选或有选错的得0
分.
9.若a>b>0,则
A.a3>b3 B.ab<b2 C. + > D. + <2
10.在平面直角坐标系xOy中,点A(- , ),角θ的终边与单位圆(圆心在原点,半径为1的圆)交于点B
(A,B不重合),下列说法正确的是
A.若cosθ=- ,则点A和点B关于x轴对称
B.若cosθ= ,则点A和点B关于y轴对称
C.若点A和点B关于直线y=-x对称,则sinθ=
D.若OA和OB相互垂直,则tanθ=
11.函数f(x)满足:x∈R,f(x+1)f(x)=2.已知当x∈[0,1)时,f(x)=2x,则
A.f(1)=1 B.f(x)为周期函数
C.f(x)为偶函数 D.方程f(x)= 恰有3个解
三、填空题:本大题共3小题,每小题5分,共15分.请把答案填写在答题卡相应位置上.
12.已知函数f(x)=log (x+2) (a>0,a≠1)的图象经过定点P(m,n),则m+n= .
a
13.已知函数f(x)= 且f(2)= ,则α= ,使得f(x)< 成立的x的取值范围是
.
14.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ< )图象的一个对称中心是(- ,0),一条对称轴是直线x=
,且f(x)在区间(0, )上有且仅有两个零点,则ω= .
四、解答题:本大题共5小题,共77分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,
证明过程或演算步骤.
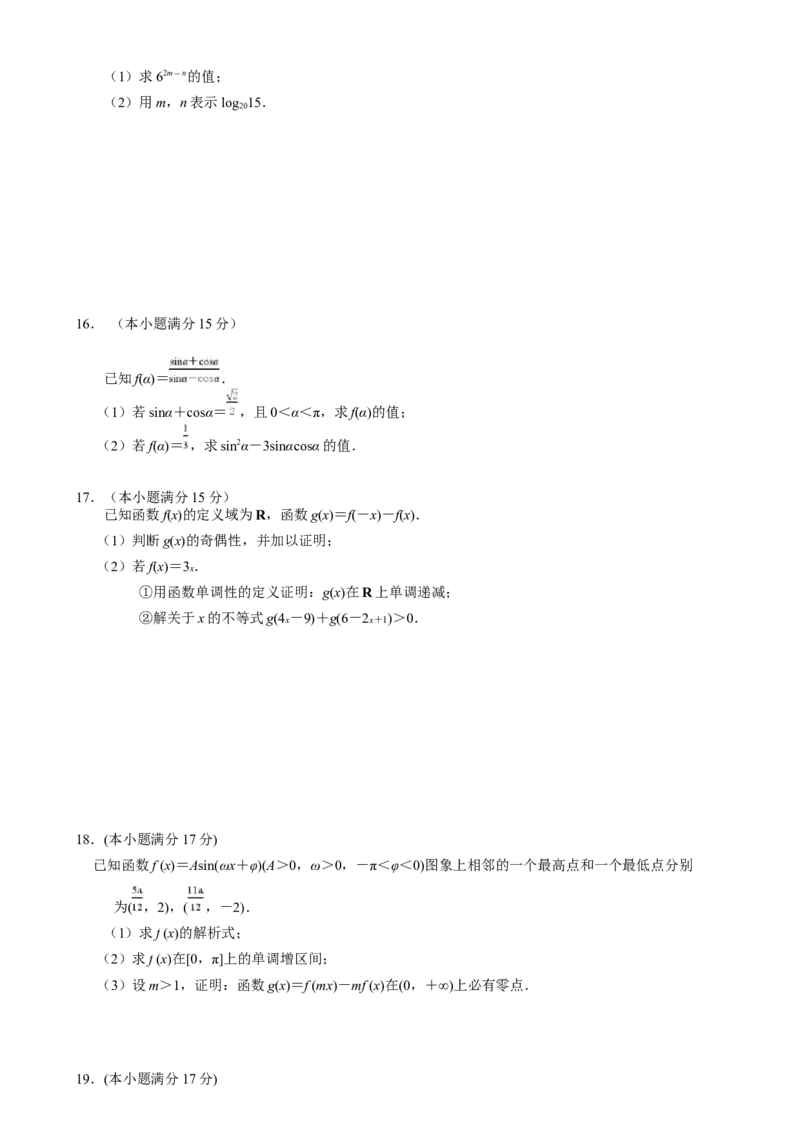
15.(本小题满分13分)
已知6m=2,6n=5.(1)求62m-n的值;
(2)用m,n表示log 15.
20
16. (本小题满分15分)
已知f(α)= .
(1)若sinα+cosα= ,且0<α<π,求f(α)的值;
(2)若f(α)= ,求sin2α-3sinαcosα的值.
17.(本小题满分15分)
已知函数f(x)的定义域为R,函数g(x)=f(-x)-f(x).
(1)判断g(x)的奇偶性,并加以证明;
(2)若f(x)=3x .
①用函数单调性的定义证明:g(x)在R上单调递减;
②解关于x的不等式g(4x -9)+g(6-2x+1)>0.
18.(本小题满分17分)
已知函数f (x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0)图象上相邻的一个最高点和一个最低点分别
为( ,2),( ,-2).
(1)求f (x)的解析式;
(2)求f (x)在[0,π]上的单调增区间;
(3)设m>1,证明:函数g(x)=f (mx)-mf (x)在(0,+∞)上必有零点.
19.(本小题满分17分)设函数f(x)在非空数集M上的取值集合为N.若N M,则称f (x)为M上的“T函数”.
(1)判断f (x)=sin2x是否为[ , ]上的“T函数”,并说明理由;
(2)若f (x)=log ( -1)为[a,b] (a<b)上的“T函数”,证明:a+b<2;
2
(3)若存在实数b,使得f (x)=(x-a)2+b为[0,1]上的“T函数”,求实数a的取值范围.
南京市 2024-2025 学年度第一学期期末学情调研测试
高一数学参考答案
2025.01
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题
目要求的,请把答案填涂在答题卡相应位置上.1.B 2.A 3.D 4.B 5.D 6.B 7.C 8.A
二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要
求,请把答案填涂在答题卡相应位置上.全部选对得6分,部分选对得部分分,不选或有错选的得0
分.
9.AC 10.ACD 11.BCD
三、填空题:本大题共3小题,每小题5分,共15分.请把答案填写在答题卡相应位置上.
12.-1 13. ,(-∞,2) 14.18
四、解答题:本大题共5小题,共77分.请在答题卡指定区域内作答,解答时应写出必要的文字说明,
证明过程或演算步骤.
15.(本小题满分13分)
解:(1)62m-n= = ;················································································5分
(2)因为6m=2,6n=5,
所以m=log 2,n=log 5.································································7分
6 6
从而log 15= ··········································································9分
20
= ··································································11分
= ,
因为log 2+log 3=1,
6 6
所以log 15= = .·················································13分
36
16. (本小题满分15分)
(1)解法1:f(α)= ,
因为sinα+cosα= ,
所以(sinα+cosα)2= ,即2sinαcosα=- ,··············································2分
从而(sinα-cosα)2=1-2sinαcosα= ,····················································4分
因为0<α<π,sinα>0,
又因为sinαcosα<0,所以cosα<0,因此sinα-cosα>0,
从而sinα-cosα= ,·········································································6分
故f(α)= = .·······································································7分
解法2:由sinα+cosα= 及sin2α+cos2α=1,····················································2分解得sinα= ,cosα= ,
或sinα= ,cosα= ,························································4分
因为 <α<π,
所以sinα= ,cosα= ,
所以sinα-cosα= ,······································································6分
因此f(α)= = = .····························································7分
(2)解法1:f(α)= = ,
所以2sinα=-4cosα,··········································································9分
假设cosα=0,则由上式知sinα=0,与sin2α+cos2α=1矛盾,
所以cosα≠0,
从而tanα=-2.················································································11分
则sin2α-3sinαcosα= = ·······································14分
= =2.·······························································15分
解法2:f(α)= = ,
所以sinα=-2cosα,
又sin2α+cos2α=1,·······································································9分
所以5cos2α=1,即cos2α= ,··························································11分
因此sin2α-3sinαcosα=4cos2α+6cos2α=10cos2α···············································14分
=2.·····························································15分
17. (本小题满分15分)
解:(1)g(x)是R上的奇函数.
因为g(x)定义域为R,对于任意的x∈R,都有-x∈R,且
g(-x)=f(x)-f(-x)=-g(x),·····························································3分
所以g(x)是R上的奇函数.·······························································4分
(2)①g(x)= -3x.
任取x,x∈R,不妨设x<x,
1 2 1 2
g(x 1 )-g(x 2 )= -3x 1 - +3x 2 =(3x 2 -3x 1)(1+ ),································7分
因为x,x∈R,x<x,且函数y=3x在R上单调递增,
1 2 1 2
所以3x
2
-3x
1
>0,1+ >0,
从而g(x)-g(x)>0,即g(x)>g(x),
1 2 1 2
因此g(x)在R上单调递减.·······························································9分
②因为g(4x-9)+g(6-2x+1)>0,
又g(x)是R上的奇函数,且单调递减,
所以g(4x-9)>g(2x+1-6),
从而4x-9<2x+1-6,·····································································12分解得-1<2x<3,
所以不等式的解集为(-∞,log 3).··················································15分
2
18.(本小题满分17分)
解:(1)由题意,A=2,··············································································1分
= - = ,又ω>0,所以 = ,即ω=2.······································3分
根据题意,当x= 时,sin(2× +φ)=1,
从而 +φ= +2kπ,k∈Z,即φ=- +2kπ,k∈Z,
又-π<φ<0,故φ=- .·································································5分
所以f (x)=2sin(2x- ).·····································································6分
(2)令- +2kπ≤2x- ≤ +2kπ,k∈Z,···················································8分
则- +2kπ≤2x≤ +2kπ,k∈Z,
即- +kπ≤x≤ +kπ,k∈Z,
所以f (x)的单调增区间为[- +kπ, +kπ],k∈Z.·····························10分
故f (x)在[0,π]上的单调增区间为[0, ]和[ ,π].······························12分
(3)g (x)=2sin(2mx- )-2msin(2x- )=2[sin(2mx- )-msin(2x- )],
当m>1时,
则g (0)= (m-1)>0,···································································14分
g ( )=2[sin( - )-m]≤2(1-m)<0,··············································16分
又g (x)在(0,+∞)上的图象是一条不间断的曲线,
所以由零点存在性定理知,
当m>1时,函数g (x)=f (mx)-mf (x)在(0,+∞)上必有零点.················17分
19.(本小题满分17分)
解:(1)由x∈[ , ],得2x∈[ , ],
所以sin2x∈[ ,1],即f (x)的取值集合为[ ,1],····································2分
因为[ ,1] [ , ],
所以f (x)=sin2x是为[ , ]上的“T函数”.········································4分
(2)因为f (x)=log ( -1)为[a,b](a<b)上的减函数,
2
所以f (x)在[a,b]的取值集合为[f (b),f (a)],·········································5分
因为f (x)为[a,b]上的“T函数”,所以[f (b),f (a)] [a,b],
因此f (b)≥a,f (a)≤b,
即log ( -1)≥a,log ( -1)≤b,···············································7分
2 2
所以(2a+1)(2b+1)≤9,(2a+1)(2b+1)≥9,
从而(2a+1)(2b+1)=9,即2a+b+2a+2b-8=0,·····································9分
因为a<b,
所以0=2a+b+2a+2b-8>2a+b+2× -8,
解得 <2,即a+b<2.·····························································11分
(3)解法1:①若a≤0,则f (x)的取值集合为[f (0),f (1)],
因此 即
从而
所以-a2+2a≥-a2,解得a≥0,
又a≤0,故a=0;········································································13分
②若0<a<1,则f (x)的取值集合为[f (a),max{f (0),f (1)}],
因此 即
从而
所以 解得0≤a≤1,
又0<a<1,故0<a<1;·································································15分
③若a≥1,则f (x)的取值集合为[f (1),f (0)],
因此 即
从而
所以-a2+1≥-a2+2a-1,解得a≤1,
又a≥1,故a=1;
综上,0≤a≤1.···················································································17分