文档内容
吕梁市 2024—2025 学年高一第一学期期末调研测试
数学试题
注意事项:
1.本试卷共4项,满分150分,考试时间120分钟.
2.答题前,考生务必用0.5毫米黑色墨迹签字笔在答题卡上填写好自己的学校、班级、姓名、准
考证号等信息将条形码横贴在答题卡“贴条形码区”.
3.考生作答时,请将答案正确地填写在答题卡上,答在本试卷上无效,
4.考试结束后,将答题卡交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知集合 ,则 ( )
A. B. C. D.
2. 命题“ ”的否定是( )
A. B.
C. D.
3. 一个扇形的圆心的为 ,弧长为 ,则其面积是( )
A. B. C. D.
4. 已知关于 一元二次不等式 的解集为 ,则 的值为( )
的
A. B. C. D.
5. 已知 ,则 的大小关系是( )A. B.
C. D.
6. 已知 ,则 ( )
A. B. C. 1 D.
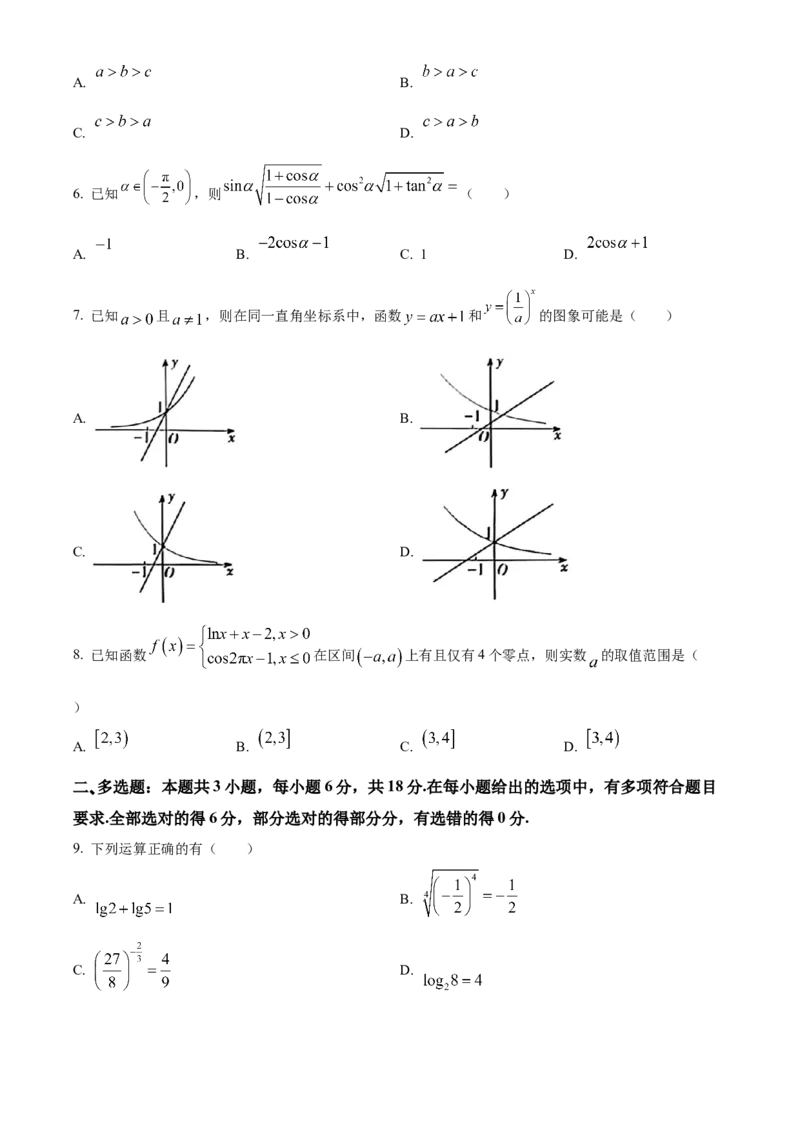
7. 已知 且 ,则在同一直角坐标系中,函数 和 的图象可能是( )
A. B.
C. D.
8. 已知函数 在区间 上有且仅有4个零点,则实数 的取值范围是(
)
A. B. C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列运算正确的有( )
A. B.
C. D.10. 已知 ,且 ,则( )
A. B.
C. D.
11. 已知 ,则( )
A. 定义域为
的
B. 的图象关于点 对称
C. 的图象关于直线 对称
D. 在区间 上单调递减
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知函数 是定义在 上的奇函数,且当 时, ,则 __________.
13. 已知函数 ,若 ,且 ,则 __________.
14. 午夜零时时针和分针重合,则午夜零时后,时针和分针第1次重合所需时间为__________小时,第3
的
次重合时时针所转 角度为__________ .
四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15. 已知角 是第三象限角,且 .
(1)求 的值;
(2)求 的值;(3)若 ,求 的值.
16. 已知函数 .
(1)求函数 的定义域;
(2)判断函数 的单调性,并用定义证明;
(3)解不等式 .
17. 山西某村为富硒土壤,且气候适宜,非常适合种植樱桃.近年来,为全面推进乡村振兴,实现共同富裕,
当地党委带领村民积极发展规模化种植,完善深加工产业链,成立深加工合作社,建立橿桃批发市场.该地
樱桃一般从5月1日开始上市,6月20日基本结束.通过市场调查,得到樱桃的投入成本 (单位:元/千
克)与上市时间 (单位:天数)的数据如下表:(上市时间 满足 )
上市时间 (天数) 10 22 50
投入成本 (元/千
3 2.16 3
克)
(1)根据上表数据,请从下列四个函数模型中选取一个恰当的函数模型反映樱桃投入成本 与上市时间
的关系(需说明理由),并求出相应的函数解析式;
① ,② ,③ ,④ .
(2)利用你选取的函数模型,求投入成本最低时樱桃的上市时间及最低投入成本.
18. 已知函数 只满足以下四个条件中的三个:① 的最
小正周期为 ;②函数 图象的两条对称轴之间的最小距离为 ;③ ;④.
(1)请找出这三个条件并说明理由,求出函数 的解析式;
(2)求 在 上的单调递增区间;
(3)若函数 在 上的值域为 ,求实数 的取值范围.
19. 在研究函数的图象与性质时,经常利用函数图象的平移思想,把一些复杂的函数转化为简单的函数.例
如函数 且 的图象可以看作把奇函数 且
的图象向右 或向左 平移 个单位长度得到的,这样我们可以得到函数
且 的图象关于点 中心对称.现有函数
.
(1)根据上面的结论,求函数 的对称中心;
(2)若 ,证明函数 在定义域内有唯一零点;
(3)当 ,函数 的图象关于点 中心对称时,若存在 , ,使得
成立,求实数 的取值范围.吕梁市 2024—2025 学年高一第一学期期末调研测试
数学试题 参考答案
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
【1题答案】
【答案】B
【2题答案】
【答案】A
【3题答案】
【答案】D
【4题答案】
【答案】B
【5题答案】
【答案】C
【6题答案】
【答案】A
【7题答案】
【答案】C
【8题答案】
【答案】B
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
【9题答案】
【答案】AC
【10题答案】
【答案】AD
【11题答案】
【答案】BCD
三、填空题:本题共3小题,每小题5分,共15分.
【12题答案】【答案】 ##0.5
【13题答案】
【答案】 ##
【14题答案】
【答案】 ①. ## ②.
四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
【15题答案】
【答案】(1)
(2)
(3) .
【16题答案】
【答案】(1)
(2) 是减函数,证明略
(3) 或 .
【17题答案】
【答案】(1)应选用函数模型 ,
为
(2)30天,最低投入成本 2元/千克.
【18题答案】【答案】(1)选②③④, ;
(2) ;
.
(3)
【19题答案】
【答案】(1) .
(2)证明略 (3) .