文档内容
格致课堂
9.2.4 总体离散程度的估计
一、选择题
1.对于一组数据x(i=1,2,3,…,n),如果将它们改变为x+C(i=1,2,3,…,n),其中C≠0,则下列结论
i i
正确的是( )
A.平均数与方差均不变 B.平均数变,方差保持不变
C.平均数不变,方差变 D.平均数与方差均发生变化
【答案】B
【解析】由平均数的定义,可知每个个体增加C,则平均数也增加C,方差不变.故选B.
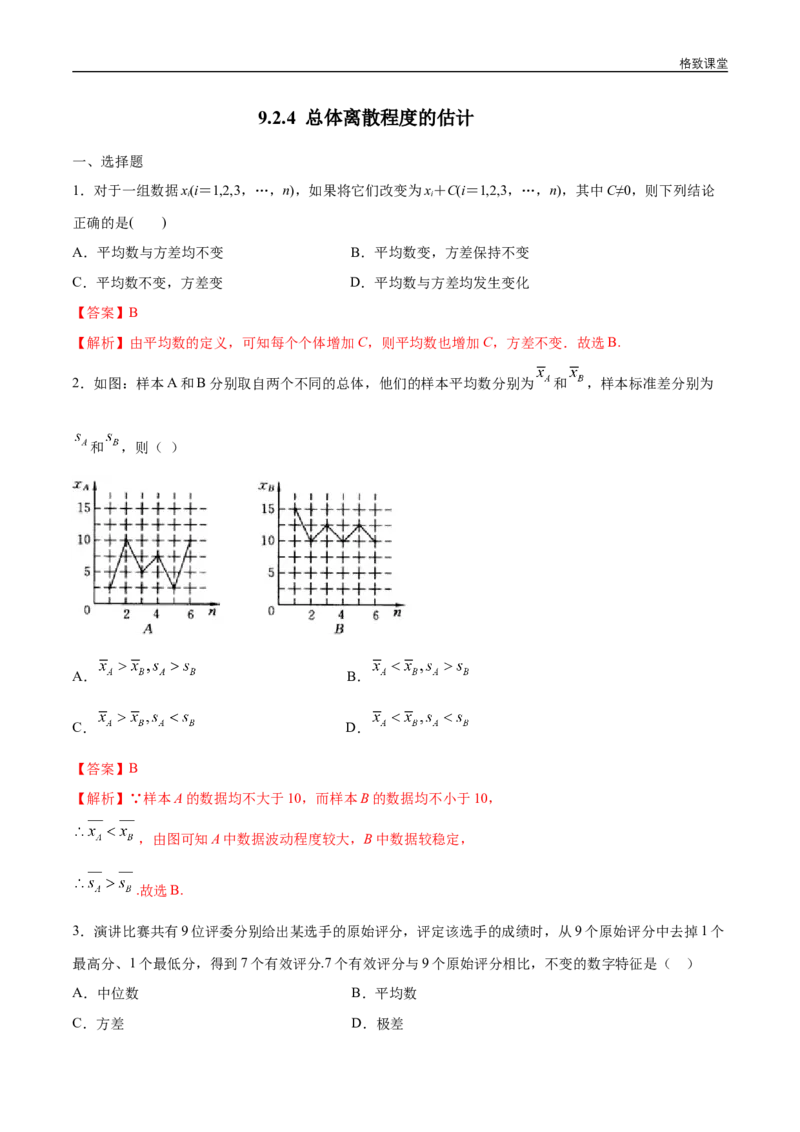
2.如图:样本A和B分别取自两个不同的总体,他们的样本平均数分别为 和 ,样本标准差分别为
和 ,则( )
A. B.
C. D.
【答案】B
【解析】∵样本A的数据均不大于10,而样本B的数据均不小于10,
,由图可知A中数据波动程度较大,B中数据较稳定,
.故选B.
3.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个
最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是( )
A.中位数 B.平均数
C.方差 D.极差格致课堂
【答案】A
【解析】设9位评委评分按从小到大排列为 .
则①原始中位数为 ,去掉最低分 ,最高分 ,后剩余 ,
中位数仍为 , A正确.②原始平均数 ,后来平均数
平均数受极端值影响较大, 与 不一定相同,B不正确
③ 由②易
知,C不正确.④原极差 ,后来极差 可能相等可能变小,D不正确.
4.某位同学参加歌唱比赛,有8位评委.歌唱结束后,各评委打分的平均数为5,方差为3.又加入一个
特邀嘉宾的打分为5,此时这9个分数的平均数为 ,方差为 ,则( )
A. , B. , C. , D. ,
【答案】B
【解析】某位同学参加歌唱比赛,有8位评委.歌唱结束后,各评委打分的平均数为5,方差为3.
又加入一个特邀嘉宾的打分为5,此时这9个分数的平均数为 ,方差为s2,
则 , .故选:B.
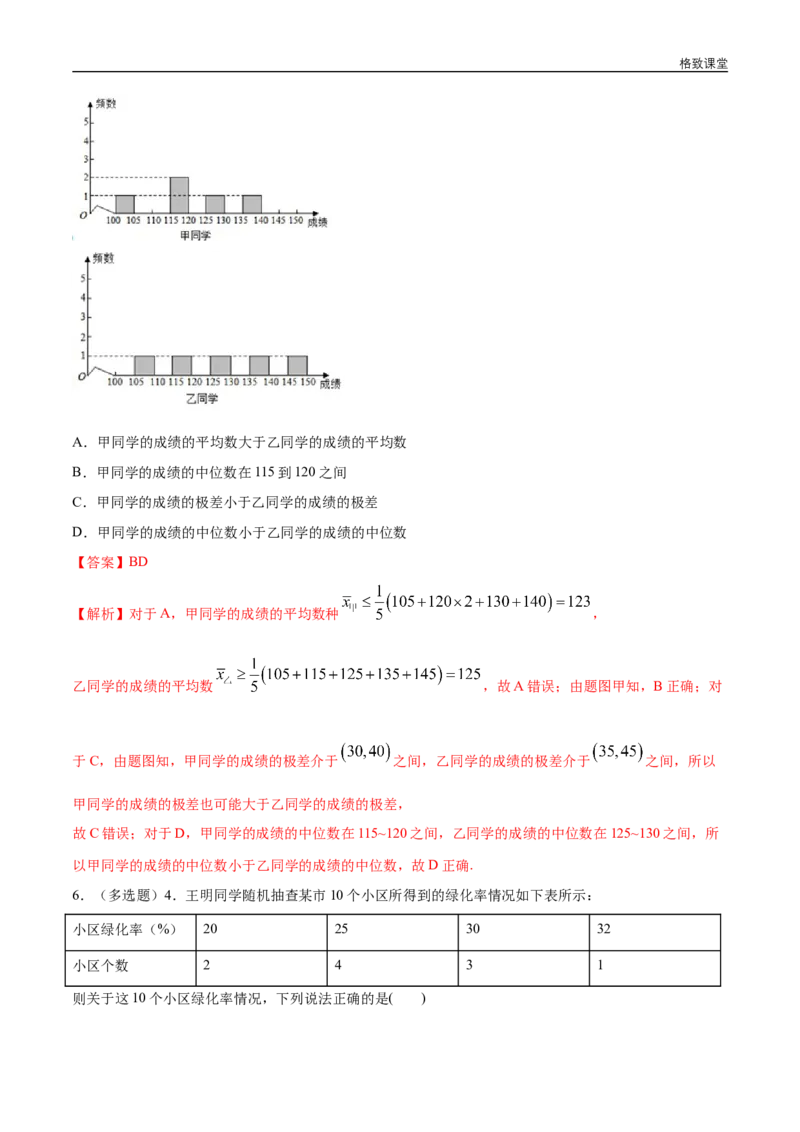
5.(多选题)下面是甲、乙两位同学高三上学期的5次联考的数学成绩,现只知其从第1次到第5次分数
所在区间段分布的条形图(从左至右依次为第1至第5次),则从图中可以读出一定正确的信息是
( )格致课堂
A.甲同学的成绩的平均数大于乙同学的成绩的平均数
B.甲同学的成绩的中位数在115到120之间
C.甲同学的成绩的极差小于乙同学的成绩的极差
D.甲同学的成绩的中位数小于乙同学的成绩的中位数
【答案】BD
【解析】对于A,甲同学的成绩的平均数种 ,
乙同学的成绩的平均数 ,故A错误;由题图甲知,B正确;对
于C,由题图知,甲同学的成绩的极差介于 之间,乙同学的成绩的极差介于 之间,所以
甲同学的成绩的极差也可能大于乙同学的成绩的极差,
故C错误;对于D,甲同学的成绩的中位数在115~120之间,乙同学的成绩的中位数在125~130之间,所
以甲同学的成绩的中位数小于乙同学的成绩的中位数,故D正确.
6.(多选题)4.王明同学随机抽查某市10个小区所得到的绿化率情况如下表所示:
小区绿化率(%) 20 25 30 32
小区个数 2 4 3 1
则关于这10个小区绿化率情况,下列说法正确的是( )格致课堂
A.方差是13% B.众数是25% C.中位数是25% D.平均数是26.2%
【答案】BCD
【解析】根据表格数据,众数为25%,选项 正确;中位数为25% ,选项 正确;
平均数为 ,选项 正确;
方差为 ;选项 错误.
二、填空题
7.国家禁毒办于 年 月 日至 月 日在全国青少年毒品预防教育数字化网络平台上开展 年
全国青少年禁毒知识答题活动,活动期间进入答题专区,点击“开始答题”按钮后,系统自动生成 道
题.已知某校高二年级有甲、乙、丙、丁、戊五位同学在这次活动中答对的题数分别是 、 、 、 、
,则这五位同学答对题数的方差是____.
【答案】
【解析】由这五位同学答对的题数分别是 、 、 、 、 ,
得该组数据的平均数 ,
则方差 .
8.某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,
方差为2,则|x﹣y|的值为_____.
【答案】4
【解析】由题意可得: ,
设 , ,则 ,解得 ,∴
9.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数格致课堂
如表所示,若以上两组数据的方差中较小的一个为 ,则 ______.
学号 1号 2号 3号 4号 5号
甲班 6 7 7 8 7
乙班 6 7 6 7 9
【答案】
【解析】由数据表可得出乙班的数据波动性较大,则其方差较大,甲班的数据波动性较小,其方差较小.则
甲班的方差为所求方差,其平均值为7,方差 .
10.某班级有50名学生,其中有30名男生和20名女生,随机询问了该班5名男生和5名女生在某次数学
测验中的成绩,5名男生的成绩分别为86,94,88,92,90,5名女生的成绩分别为88,93,93,88,93.
①这种抽样方法是一种分层随机抽样;
②这5名男生成绩的方差大于这5名女生成绩的方差;
③该班男生成绩的平均数小于该班女生成绩的平均数.
则以上说法一定正确的是______.
【答案】②.
【解析】若抽样方法是分层随机抽样,男生、女生分别抽取 人、 人,故①错误;
这 名男生成绩的平均数:
这 名女生成绩的平均数:
这 名男生成绩的方差:
这 名女生成绩的方差: ,故②正确;
由题所给的条件只能得出这 名男生成绩的平均数小于这 名女生成绩的平均数,不能说明班级总体情况,格致课堂
故③错误.故答案为:②
三、解答题
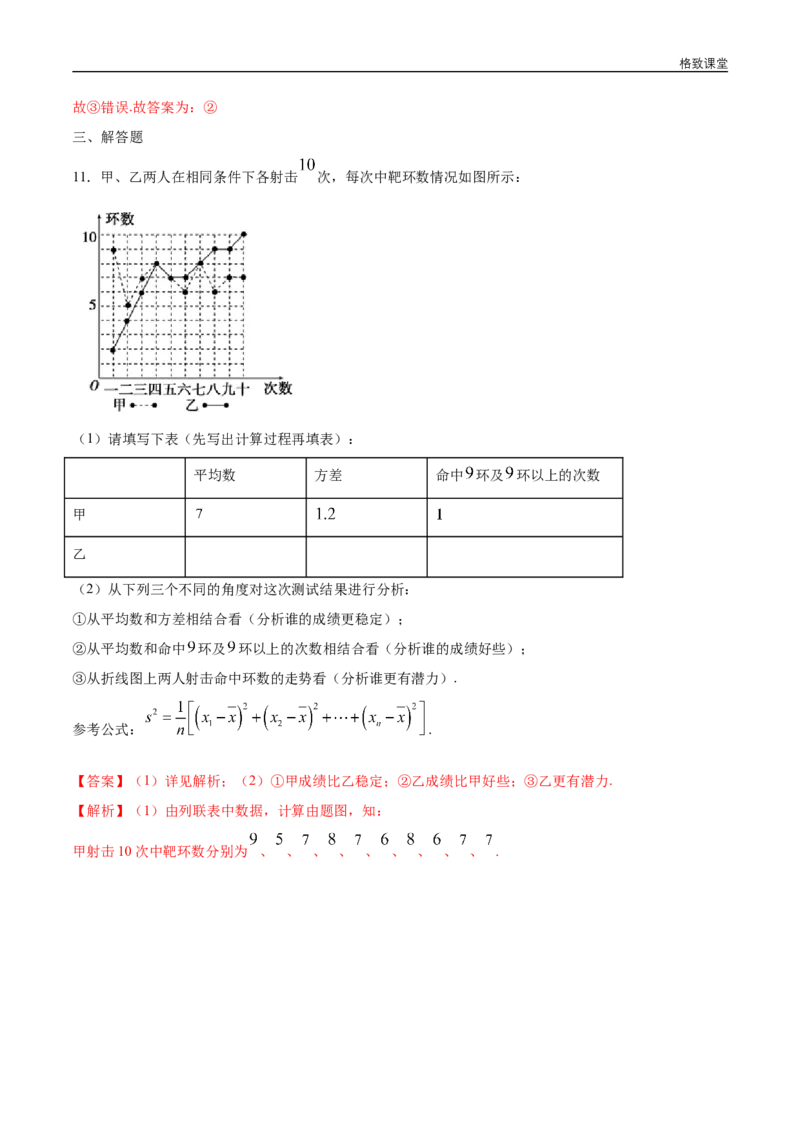
11.甲、乙两人在相同条件下各射击 次,每次中靶环数情况如图所示:
(1)请填写下表(先写出计算过程再填表):
平均数 方差 命中 环及 环以上的次数
甲
乙
(2)从下列三个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中 环及 环以上的次数相结合看(分析谁的成绩好些);
③从折线图上两人射击命中环数的走势看(分析谁更有潜力).
参考公式: .
【答案】(1)详见解析;(2)①甲成绩比乙稳定;②乙成绩比甲好些;③乙更有潜力.
【解析】(1)由列联表中数据,计算由题图,知:
甲射击10次中靶环数分别为 、 、 、 、 、 、 、 、 、 .格致课堂
将它们由小到大排列为 、 、 、 、 、 、 、 、 、 .
乙射击 次中靶环数分别为 、 、 、 、 、 、 、 、 、 .
将它们由小到大排列为 、 、 、 、 、 、 、 、 、 ;
(1) (环),
.
填表如下:
平均数 方差 命中 环及 环以上的次数
甲
乙
(2)① 平均数相同, , 甲成绩比乙稳定;
② 平均数相同,命中 环及 环以上的次数甲比乙少, 乙成绩比甲好些;
③甲成绩在平均数上下波动;而乙处于上升势头,从第三次以后就没有比甲少的情况发生,
乙更有潜力.
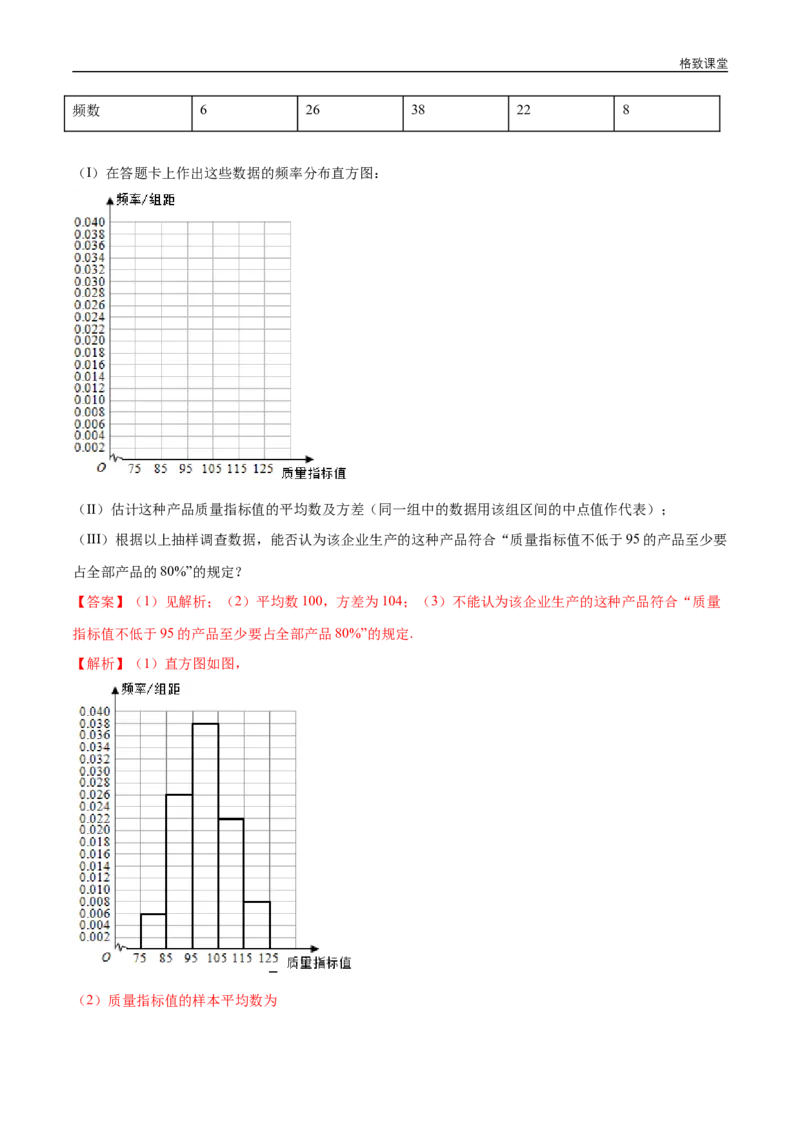
12.从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布
表:
质量指标值分组 [75,85) [85,95) [95,105) [105,115) [115,125)格致课堂
频数 6 26 38 22 8
(I)在答题卡上作出这些数据的频率分布直方图:
(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要
占全部产品的80%”的规定?
【答案】(1)见解析;(2)平均数100,方差为104;(3)不能认为该企业生产的这种产品符合“质量
指标值不低于95的产品至少要占全部产品80%”的规定.
【解析】(1)直方图如图,
(2)质量指标值的样本平均数为格致课堂
.
质量指标值的样本方差为
.
(3)质量指标值不低于95的产品所占比例的估计值为
,
由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全
部产品80%”的规定.