文档内容
1993 年青海高考文科数学真题及答案
一.选择题:本题共18个小题;每小题3分,共54分。在每小题给出的四个选项中,只
有一项是符合题目要求的。把所选项前的字母填在题后括号内。
(1)若双曲线实半轴长为2,焦距为6,那么离心率是 ( C )
(A) (B) (C) (D)2
(2)函数 的最小正周期是 ( B )
(A) (B) (C) (D)
(3)当圆锥的侧面积和底面积的比值是 时,圆锥的轴截面顶角是
(A)450 (B)600 (C)900 (D)1200 ( C )
(4)当 时, 的值等于 ( D )
(A)1 (B)-1 (C)i (D)-i
(5)若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是
(A)三棱锥 (B)四棱锥 (C)五棱锥 (D)六棱锥 ( D )
(6)在直角三角形中两锐角为A和B,则sinAsinB ( B )
(A)有最大值 和最小值0 (B)有最大值 ,但无最小值
(C)即无最大值也无最小值 (D)有最大值1,但无最小值
(7)在各项均为正数的等比数列 中,若 ,则
( B )
(A)12 (B)10 (C)8 (D)
(8) 是偶函数,且 不恒等于零,则
( A )
第1页 | 共7页(A)是奇函数 (B)是偶函数
(C)可能是奇函数也可能是偶函数 (D)不是奇函数也不是偶函数
(9)设直线 与y轴的交点为P,点P把圆 的直径分为两段,
则其长度之比为 ( A )
(A) (B) (C) (D)
(10)若 是任意实数,且 ,则 ( D )
(A) (B) (C) (D)
(11)已知集合 ,那么 为区
间 ( A )
(A) (B) (C) (D)
(12)一动圆与两圆:x2+y2=1和x2+y2-8x+12=0都外切,则动圆圆心的轨迹为
( C )
(A)抛物线 (B)圆 (C)双曲线的一支 (D)椭圆
(13)若直线ax+by+c=0在第一、二、三象限,则 ( D )
(A)ab>0,bc>0(B)ab>0,bc<0(C)ab<0,bc>0 (D)ab<0,bc<0
(14)如果圆柱轴截面的周长 为定值,那么圆柱体积的最大值是
( A )
(A) (B) (C) (D)
(15)由 展开所得的x的多项式中,系数为有理数的共有
( B )
(A)50项 (B)17项 (C)16项 (D)15项
(16)设 都是正数,且 ,那么 ( B )
(A) (B) (C) (D)
(17)同室四人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,
第2页 | 共7页则四张贺年卡不同的分配方式有 ( B )
(A)6种 (B)9种 (C)11种 (D)23种
(18)在正方体ABCD-ABCD中,M、N分别为棱AA和BB的中点(如图)。若 为直线CM
1 1 1 1 1 1
与DN所成的角,则 ( D )
1
D C A
D C 1 1 1
(A) (B) 1 1
A B
1 1
(C) (D)
M N B
1
二.填空题:本大题共6小题;每小题3分,共18分。 把答案 D 1 C 1 A 1
D C D C A
填在题中横线上。 B
A B
(19)抛物线y2=4x的弦AB垂直于x轴,若AB的长 为 ,
B
1 D C A
则焦点到AB的距离为________________. 1 1 1
D C A
[答]:2
B
(20)在半径为30m的圆形广场中央上空,设置一个照明光源,射向地面的光呈圆锥形,
B
1
且其轴截面顶角为1200。若要光源恰好照亮整个广场,则其高度应为________m(精确
D C A
到).
B
[答]:
(21)在50件产品中有4件是次品,从中任意抽出5件,至少有3件是次品的抽法共
_________种(用数字作答).
[答]:4186
(22)建造一个容积为8m3,深为2m的长方体无盖水池。如果池底和池壁的造价每平方米分
别为120元和80元,那么水池的最低造价为_______元.
[答]:1760
(23)设 ,则 =__________
[答]:1
(24)设 ____________
[答]:-1
三.解答题:本大题共5小题;共48分.解答应写出文字说明、演算步骤。
第3页 | 共7页(25)(本小题满分8分)
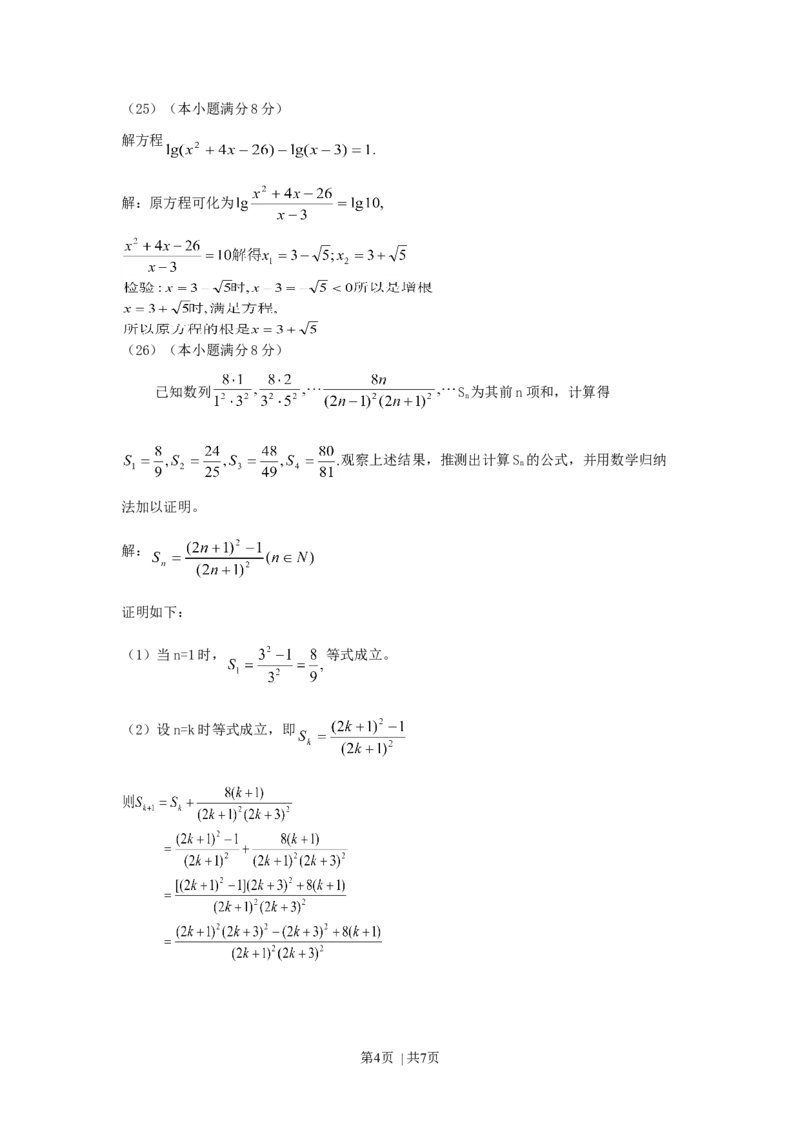
解方程
解:原方程可化为
(26)(本小题满分8分)
已知数列 S 为其前n项和,计算得
n
观察上述结果,推测出计算S 的公式,并用数学归纳
n
法加以证明。
解:
证明如下:
(1)当n=1时, 等式成立。
(2)设n=k时等式成立,即
第4页 | 共7页由此可知,当n=k+1时等式也成立
根据(1),(2)可知,等式对任何 都成立。
(27)(本小题满分10分)
如图,ABC-ABC是直三棱柱,过点A、B、C 的平面和平面ABC的交线记作L。
1 1 1 1 1
(Ⅰ)判定直线AC 和L的位置关系,并加以证明;
1 1
(Ⅱ)若AA=1,AB=4,BC=3,∠ABC=900,求顶点A 到直线L的距离。
1 1
解:(Ⅰ)L∥AC 证明如下:
1 1
A
1
根据棱柱的定义知
平面A 1 B 1 C 1 和平面ABC平行。 C 1
B
由题设知直线 1
A D
AC=平面ABC∩平面ABC,
1 1 1 1 1 1 1
E
直线L=平面ABC∩平面ABC, 根据两平
1 1 1 1 1 L C
面平行的性质定理 B
有L∥AC
1 1
(Ⅱ)过点A 作AE⊥L于E,则AE的长为点A 到L的距离。连接AE,由直棱柱的定义知
1 1 1 1
AA⊥平面ABC
1
∴直线AE是直线AE在平面ABC上的射影。
1
又L在平面ABC上,根据三垂线定理的逆定理有AE⊥L
由棱柱的定义质AC∥AC,又L∥AC,∴L∥AC
1 1 1 1
作BD⊥AC于D,
则BD是Rt△ABC斜边AC上的高,且BD=AE,
从而
在Rt△AAE中,∵AA=1,∠AAE=900,
1 1 1
第5页 | 共7页∴
故点A 到直线L的距离为
1
(28)(本小题满分10分)
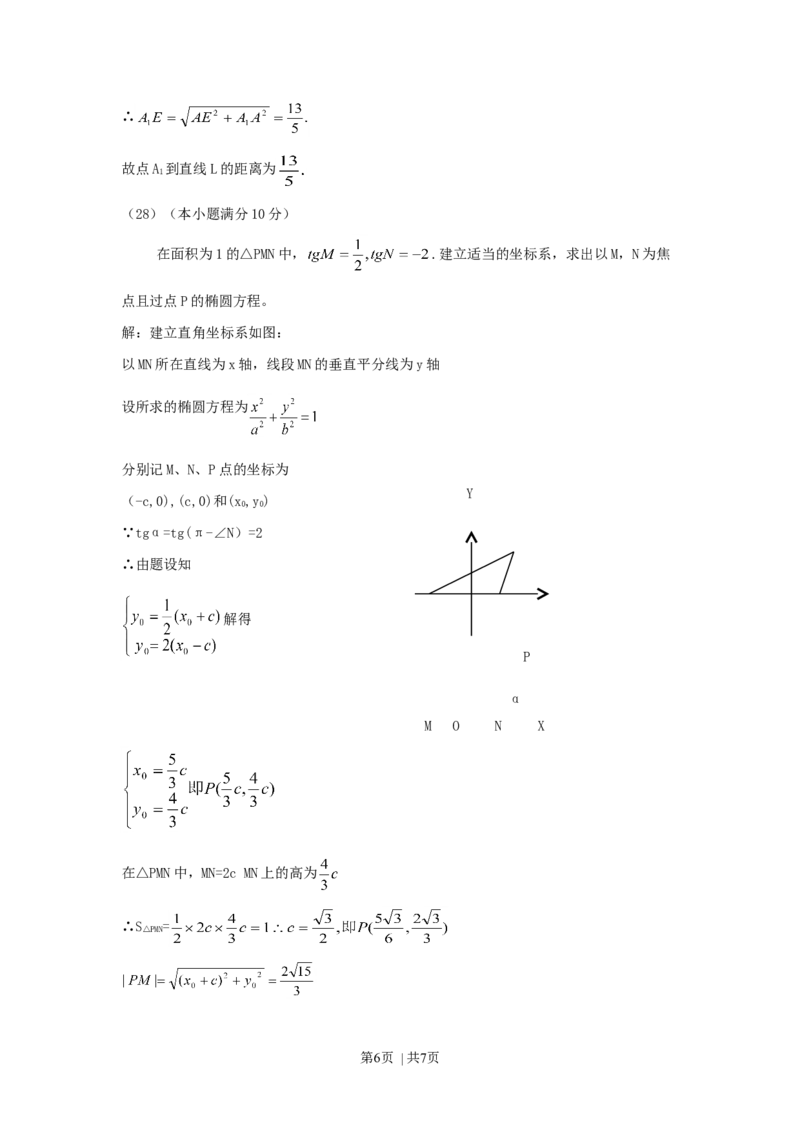
在面积为1的△PMN中, .建立适当的坐标系,求出以M,N为焦
点且过点P的椭圆方程。
解:建立直角坐标系如图:
以MN所在直线为x轴,线段MN的垂直平分线为y轴
设所求的椭圆方程为
分别记M、N、P点的坐标为
Y
(-c,0),(c,0)和(x,y)
0 0
∵tgα=tg(π-∠N)=2
∴由题设知
解得
P
α
M O N X
在△PMN中,MN=2c MN上的高为
∴S =
△PMN
第6页 | 共7页故所求椭圆方程为
(29)(本小题满分12分)
设复数 求 。
解:
第7页 | 共7页