四川省南充市2024届高三高考适应性考试（二诊）理科数学试题_2024年3月_013月合集_2024届四川省南充市高三高考适应性考试（二诊）

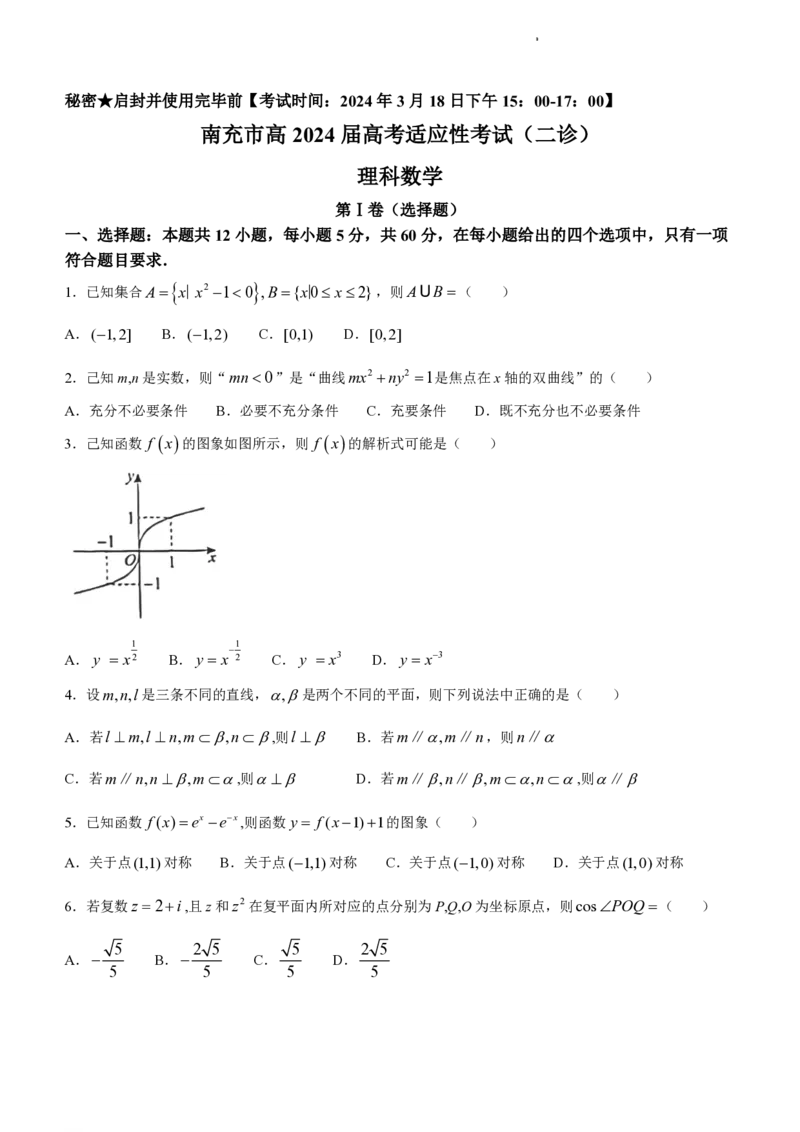
秘密★启封并使用完毕前【考试时间：2024年 3月 18日下午 15：00-17：00】 南充市高 2024 届高考适应性考试（二诊） 理科数学 第Ⅰ卷（选择题） 一、选择题：本题共 12小题，每小题 5 分，共 60分，在每小题给出的四个选项中，只有一项 符合题目要求． 1．已知集合A  x∣x2 10  ,B{x∣0 x2}，则AUB（ ） A．(1,2] B．(1,2) C．[0,1) D．[0,2] 2．己知m,n是实数，则“mn0”是“曲线mx2 ny2 1是焦点在x轴的双曲线”的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 3．己知函数 f x的图象如图所示，则 f x的解析式可能是（ ） 1 1  A．y  x2 B．y  x 2 C．y  x3 D．y  x3 4．设m,n,l是三条不同的直线，,是两个不同的平面，则下列说法中正确的是（ ） A．若l m,l n,m,n,则l  B．若m∥,m∥n，则n∥ C．若m∥n,n,m,则 D．若m∥,n∥,m,n,则∥ 5．已知函数 f(x)ex ex,则函数y  f(x1)1的图象（ ） A．关于点(1,1)对称 B．关于点(1,1)对称 C．关于点(1,0)对称 D．关于点(1,0)对称 6．若复数z 2i,且z和z2在复平面内所对应的点分别为P,Q,O为坐标原点，则cosPOQ（ ） 5 2 5 5 2 5 A． B． C． D． 5 5 5 5 学学科科网网（（北北京京））股股份份有有限限公公司司x y6  7．已知点Px ,y 为可行域4x y 0内任意一点，则x  y 0的概率为（ ） 0 0 0 0  x,yN*  1 2 4 2 A． B． C． D． 3 3 9 9   8．已知函数 f(x)3sinx4cosx．设x时， f(x)取得最大值．则cos    （ ）  4 7 2 7 2 2 2 A． B． C． D． 10 10 10 10 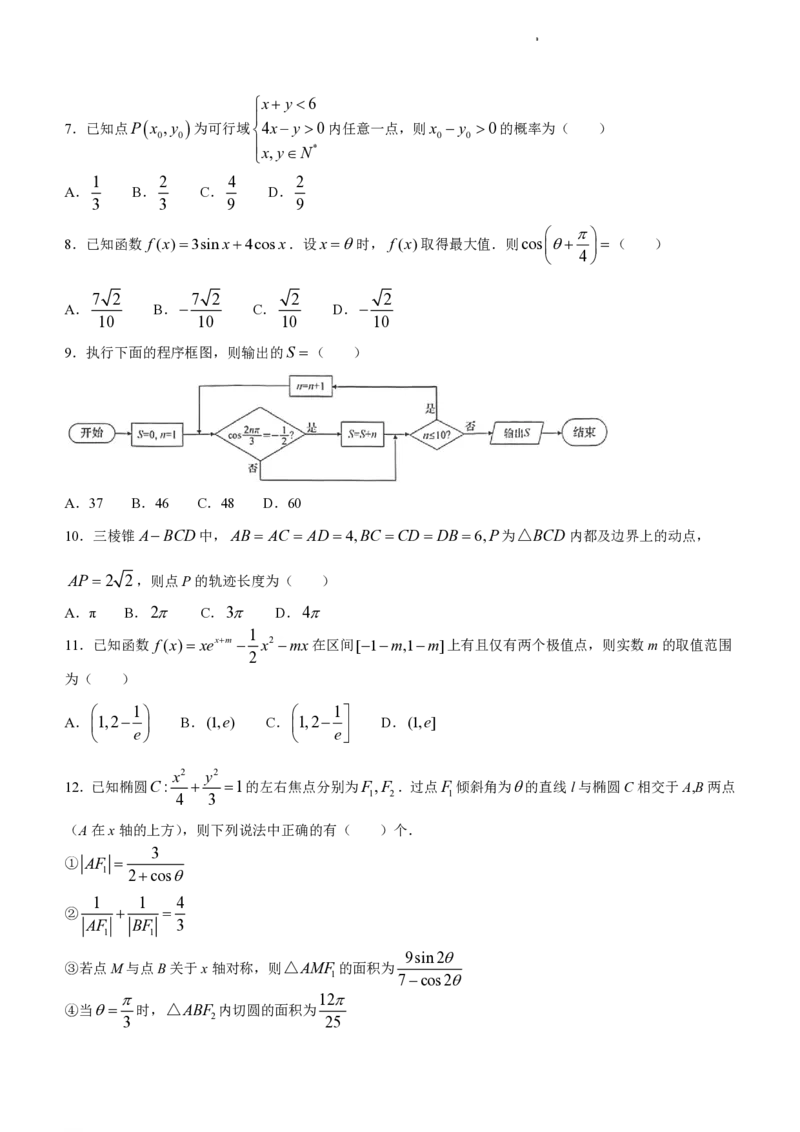9．执行下面的程序框图，则输出的S （ ） A．37 B．46 C．48 D．60 10．三棱锥ABCD中，AB AC  AD4,BC CD DB6,P为△BCD内都及边界上的动点， AP2 2，则点P的轨迹长度为（ ） A．π B．2 C．3 D．4 1 11．已知函数 f(x) xexm  x2 mx在区间[1m,1m]上有且仅有两个极值点，则实数m的取值范围 2 为（ ）  1  1 A．  1,2  B．(1,e) C．  1,2  D．(1,e]  e  e x2 y2 12．已知椭圆C:  1的左右焦点分别为F,F ．过点F 倾斜角为的直线l与椭圆C相交于A,B两点 4 3 1 2 1 （A在x轴的上方），则下列说法中正确的有（ ）个． 3 ① AF  1 2cos 1 1 4 ②   AF BF 3 1 1 9sin2 ③若点M与点B关于x轴对称，则△AMF 的面积为 1 7cos2  12 ④当 时，△ABF 内切圆的面积为 3 2 25 学学科科网网（（北北京京））股股份份有有限限公公司司A．1 B．2 C．3 D．4 二．填空题：本大题共 4小题，每小题 5 分，共 20分．把答案填在答题卡上． r r r r 13．已知a (3,4),b (m,m1),a∥b ,则m__________ 1 1 14．已知x,y是实数，x0,y 0,且x y 4,则  的最小值为__________ x y 15．在△ABC中，a,b,c分别为内角A,B,C的对边．已知a 2,2sinB2sinC 3sin A．则sinA的最大值 为__________ 16．“曼哈顿距离”是人脸识别中一种重要的测距方式．其定义如下： 设Ax ,y ,Bx ,y 是坐标平面内的两点，则A,B两点间的曼哈顿距离为d(A,B) x x  y  y ． 1 1 2 2 1 2 1 2 在平面直角坐标系中xOy中，下列说法中正确说法的序号为__________ ①．若A(2,3),B(3,2),则d(A,B)6; ②．若O为坐标原点，且动点P满足：d(O,P)1,则P的轨迹长度为4 2； ③．设M(a,b)是坐标平面内的定点，动点N满足：d(M,N)2,则N的轨迹是以点 (a2,b),(a2,b),(a,b2),(a,b2)为顶点的正方形； ④．设R(1,1),Q(|x|,| y|),d(R,Q)1，则动点(x,y)构成的平面区域的面积为10． 三、解答题：共 70分．解答应写出文字说明、证明过程或演算步骤．第 17—21题必考题，每 个试题考生必须作答．第 22、23题为选考题，考试根据要求作答． （一）必考题：共 60分． 17．在数列a 中，S 是其前n项和，且3S a 64． n n n n （1）．求数列a 的通项公式； n （2）．若nN ,1S 44恒成立，求的取值范围．  n 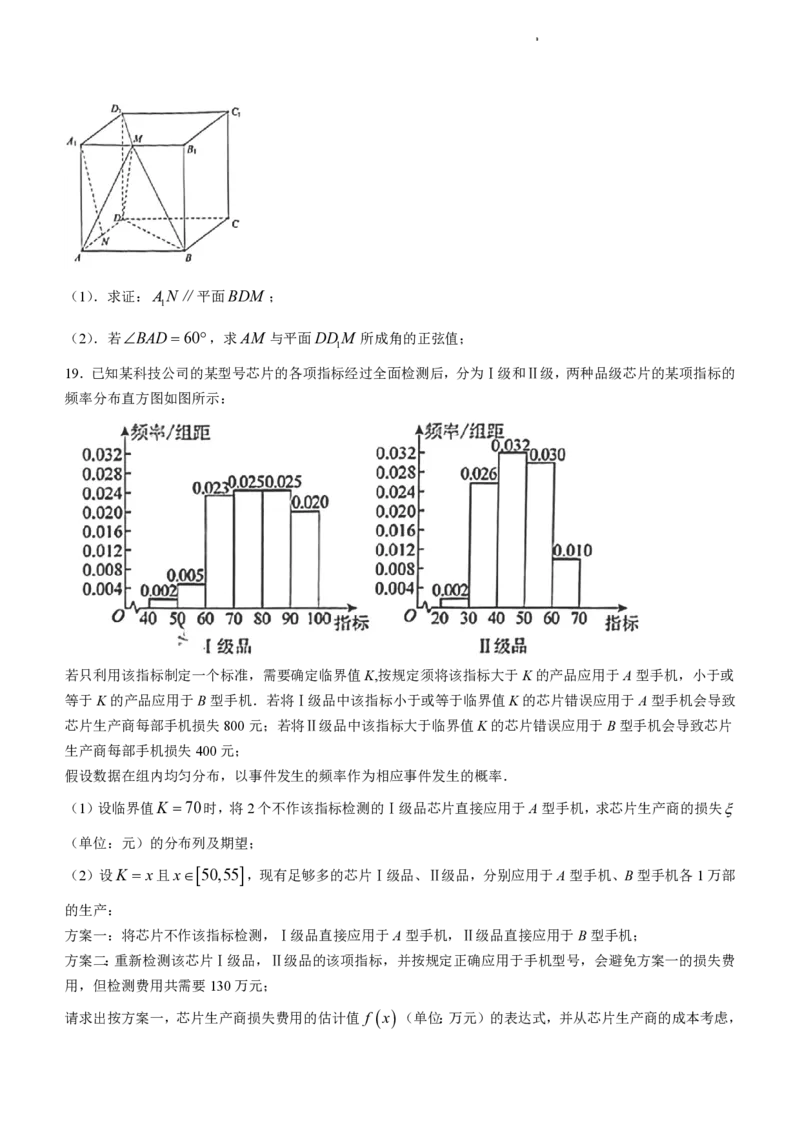18．如图所示，在直四棱柱ABCDABC D 中，底面ABCD是菱形，AB AA 4,M,N 分别为AB,AD 1 1 1 1 1 1 1 的中点． 学学科科网网（（北北京京））股股份份有有限限公公司司（1）．求证：AN∥平面BDM ； 1 （2）．若BAD60，求AM 与平面DDM 所成角的正弦值； 1 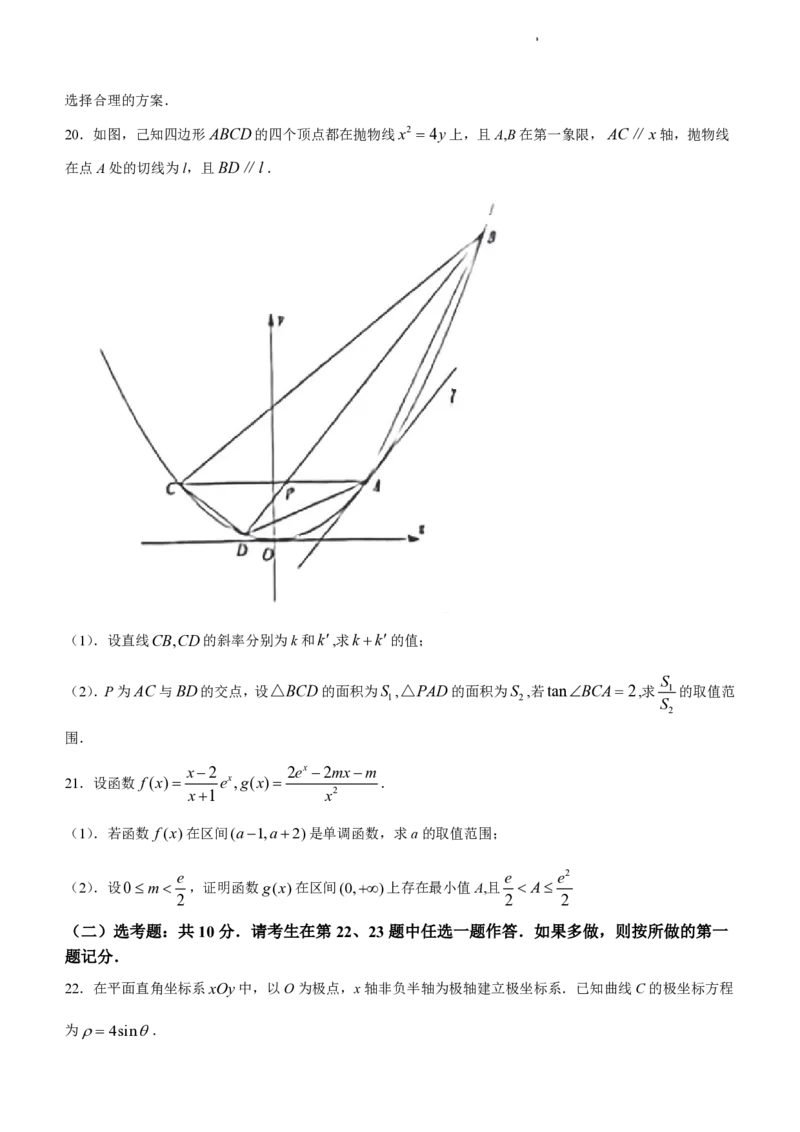19．已知某科技公司的某型号芯片的各项指标经过全面检测后，分为Ⅰ级和Ⅱ级，两种品级芯片的某项指标的 频率分布直方图如图所示： 若只利用该指标制定一个标准，需要确定临界值K,按规定须将该指标大于K的产品应用于A型手机，小于或 等于K的产品应用于B型手机．若将Ⅰ级品中该指标小于或等于临界值K的芯片错误应用于A型手机会导致 芯片生产商每部手机损失800元；若将Ⅱ级品中该指标大于临界值K的芯片错误应用于B型手机会导致芯片 生产商每部手机损失400元； 假设数据在组内均匀分布，以事件发生的频率作为相应事件发生的概率． （1）设临界值K 70时，将2个不作该指标检测的Ⅰ级品芯片直接应用于A型手机，求芯片生产商的损失 （单位：元）的分布列及期望； （2）设K  x且x50,55，现有足够多的芯片Ⅰ级品、Ⅱ级品，分别应用于A型手机、B型手机各1万部 的生产： 方案一：将芯片不作该指标检测，Ⅰ级品直接应用于A型手机，Ⅱ级品直接应用于B型手机； 方案二：重新检测该芯片Ⅰ级品，Ⅱ级品的该项指标，并按规定正确应用于手机型号，会避免方案一的损失费 用，但检测费用共需要130万元； 请求出按方案一，芯片生产商损失费用的估计值 f x（单位：万元）的表达式，并从芯片生产商的成本考虑， 学学科科网网（（北北京京））股股份份有有限限公公司司选择合理的方案． 20．如图，己知四边形ABCD的四个顶点都在抛物线x2 4y上，且A,B在第一象限，AC∥x轴，抛物线 在点A处的切线为l，且BD∥l． （1）．设直线CB,CD的斜率分别为k和k,求kk的值； S （2）．P为AC与BD的交点，设△BCD的面积为S ,△PAD的面积为S ,若tanBCA2,求 1 的取值范 1 2 S 2 围． x2 2ex 2mxm 21．设函数 f(x) ex,g(x) ． x1 x2 （1）．若函数 f(x)在区间(a1,a2)是单调函数，求a的取值范围； e e e2 （2）．设0m ，证明函数g(x)在区间(0,)上存在最小值A,且  A 2 2 2 （二）选考题：共 10分．请考生在第 22、23题中任选一题作答．如果多做，则按所做的第一 题记分． 22．在平面直角坐标系xOy中，以O为极点，x轴非负半轴为极轴建立极坐标系．已知曲线C的极坐标方程 为4sin． 学学科科网网（（北北京京））股股份份有有限限公公司司（1）．求曲线C在直角坐标系中的普通方程； uuur uuur uuur uuur 2 2 （2）．已知P(1,2),直线l:x y 3与曲线C交于A,B两点，求PA PB PAPB的值． 23．已知函数 f(x)|2x2||2xa|． （1）．当a 2时，画出 f(x)的图象，并根据图象写出函数 f(x)的值域； （2）．若关于x的不等式 f(x)2aa2有解，求a的取值范围． 学学科科网网（（北北京京））股股份份有有限限公公司司