文档内容
第四章 指数函数与对数函数章末检测
时间:120分钟 分值:150分
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一项是符合题目要求的)
1. 函数y= 的定义域为( )
A.(-∞,2) B.(2,+∞)
C.(2,3)∪(3,+∞) D.(2,4)∪(4,+∞)
2.函数f(x)= 的值域是( )
A.(-∞,1) B.(0,1)
C.(1,+∞) D.(-∞,1)∪(1,+∞)
3.函数 的零点为( )
A. 或 B.
C. D. 或(
4.已知 , ,则 用 表示为( )
A. B.
C. D.
5.若镭经过100年后剩留原来质量的 ,设质量为1的镭经过 年后剩留量为 ,
则 , 的函数关系是( )
A. B.
C. D.
6.已知 , , ,则( )
A. B.
C. D.7.设函数 与 的图象的交点为 ,则 所在的区间为(
)
A. B.
C. D.
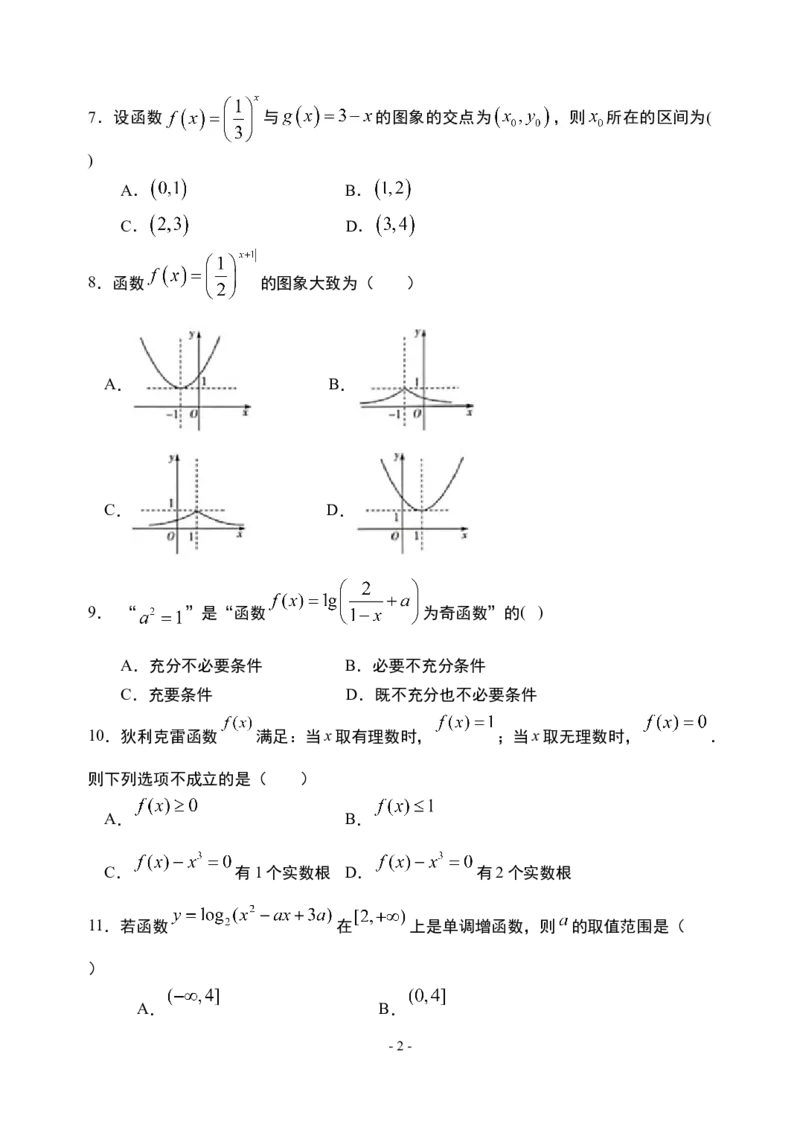
8.函数 的图象大致为( )
A. B.
C. D.
9. “ ”是“函数 为奇函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
10.狄利克雷函数 满足:当x取有理数时, ;当x取无理数时, .
则下列选项不成立的是( )
A. B.
C. 有1个实数根 D. 有2个实数根
11.若函数 在 上是单调增函数,则 的取值范围是(
)
A. B.
- 2 -C. D.
12.已知函数 ,若函数 恰有 个零
点,则实数 不可能是( )
A. B.
C. D.
二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)
13.设 ,则 ________.
14.函数 和 的图像的示意图如图所示,
设两函数的图像交于点 , ,且 .
若 , ,
且 , ,则 _______.
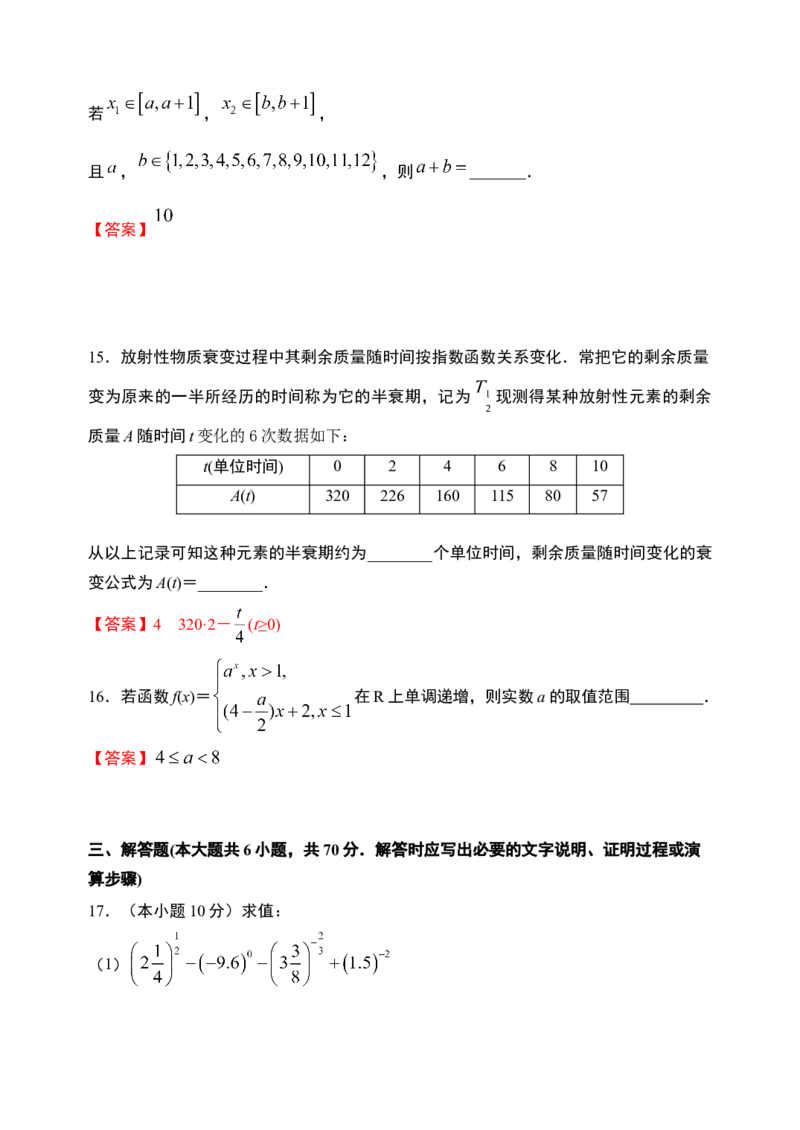
15.放射性物质衰变过程中其剩余质量随时间按指数函数关系变化.常把它的剩余质量
变为原来的一半所经历的时间称为它的半衰期,记为 现测得某种放射性元素的剩余质
量A随时间t变化的6次数据如下:
t(单位时间) 0 2 4 6 8 10
A(t) 320 226 160 115 80 57
从以上记录可知这种元素的半衰期约为________个单位时间,剩余质量随时间变化的衰
变公式为A(t)=________.16.若函数f(x)= 在R上单调递增,则实数a的取值范围 .
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演
算步骤)
17.(本小题10分)求值:
(1) ;
(2) .
18.(本小题12分)
函数 , 的图象如图所示.
(1)指出曲线C ,C 分别对应哪一个函数;
1 2
(2)比较两函数的增长差异(以两图象交点为分界点,对 , 的大小进行比较).
19.(本小题12分)
已知函数 ,
- 4 -(1)若它的定义域为 ,求实数a的取值范围;
(2)若它的值域为 ,求实数a的取值范围.
20.(本小题12分)
已知 , ,
(1)设 , , ,求 的最大值与最小值;
(2)求 的最大值与最小值.
21.(本小题12分)
已知函数 .
(1)求函数 的定义域;
(2)求函数 的零点;
(3)若函数 的最小值为 ,求 的值.
22.(本小题12分)
十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在
大力实施一项将重塑全球汽车行业的计划.2018年某企业计划引进新能源汽车生产设备,
通过市场分析,全年需投入固定成本2500万元,每生产x(百辆),需另投入成本
万元,且 .由市场调研知,每辆车售价5
万元,且全年内生产的车辆当年能全部销售完.
(1)求出2018年的利润L(x)(万元)关于年产量x(百辆)的函数关系式;(利润=
销售额-成本)(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
第四章 指数函数与对数函数章末检测参考答案
时间:120分钟 分值:150分
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一项是符合题目要求的)
1. 函数y= 的定义域为( )
A.(-∞,2) B.(2,+∞)
C.(2,3)∪(3,+∞) D.(2,4)∪(4,+∞)
【答案】C
2.函数f(x)= 的值域是( )
A.(-∞,1) B.(0,1)
C.(1,+∞) D.(-∞,1)∪(1,+∞)
【答案】B
3.函数 的零点为( )
A. 或 B.
C. D. 或(
【答案】B
4.已知 , ,则 用 表示为( )
A. B.
C. D.
【答案】A
5.若镭经过100年后剩留原来质量的 ,设质量为1的镭经过 年后剩留量为 ,
则 , 的函数关系是( )
A. B.
C. D.
- 6 -【答案】A
6.已知 , , ,则( )
A. B.
C. D.
【答案】C
7.设函数 与 的图象的交点为 ,则 所在的区间为(
)
A. B.
C. D.
【答案】C
8.函数 的图象大致为( )
A. B.
C. D.
【答案】B
9. “ ”是“函数 为奇函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】B10.狄利克雷函数 满足:当x取有理数时, ;当x取无理数时, .
则下列选项不成立的是( )
A. B.
C. 有1个实数根 D. 有2个实数根
【答案】D
11.若函数 在 上是单调增函数,则 的取值范围是(
)
A. B.
C. D.
【答案】C
12.已知函数 ,若函数 恰有 个零
点,则实数 不可能是( )
A. B.
C. D.
【答案】D
二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)
13.设 ,则 ________.
【答案】
14.函数 和 的图像的示意图如图所示,设两函数的图像交于点
, ,且 .
- 8 -若 , ,
且 , ,则 _______.
【答案】
15.放射性物质衰变过程中其剩余质量随时间按指数函数关系变化.常把它的剩余质量
变为原来的一半所经历的时间称为它的半衰期,记为 现测得某种放射性元素的剩余
质量A随时间t变化的6次数据如下:
t(单位时间) 0 2 4 6 8 10
A(t) 320 226 160 115 80 57
从以上记录可知这种元素的半衰期约为________个单位时间,剩余质量随时间变化的衰
变公式为A(t)=________.
【答案】4 320·2- (t≥0)
16.若函数f(x)= 在R上单调递增,则实数a的取值范围 .
【答案】
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演
算步骤)
17.(本小题10分)求值:
(1)(2)
【答案】
(1)原式= =
(2)原式
18.(本小题12分)
函数 , 的图象如图所示.
(1)指出曲线C ,C 分别对应哪一个函数;
1 2
(2)比较两函数的增长差异(以两图象交点为分界点,对 , 的大小进行比较).
【答案】
(1)由题图知,C 对应的函数为 ,C 对应的函数为 .
1 2
(2)当x∈(0,x)时,g(x)>f(x);
1
当x∈(x,x)时,g(x)<f(x);
1 2
当x∈(x,+∞)时,g(x)>f(x).
2
19.(本小题12分)
已知函数 ,
(1)若它的定义域为 ,求实数a的取值范围;
(2)若它的值域为 ,求实数a的取值范围.
【答案】函数 的定义域为 ,则 恒成立,故
,即 ;
- 10 -函数 为 ,则 是函数 值域的子集,
则 ,即 .
20.(本小题12分)
已知 , ,
(1)设 , , ,求 的最大值与最小值;
(2)求 的最大值与最小值.
【答案】(1)设 , , ,则 ,即 ,
即 的最大值为9,最小值为1;
(2)设 , , ,则 ,
函数 转化为 ,
,
当 时, 最小为 ,
当 时, 最大为 ,
即 的最大值为67,最小值3.
21.(本小题12分)
已知函数 .
(1)求函数 的定义域;
(2)求函数 的零点;(3)若函数 的最小值为 ,求 的值.
【答案】(1)由已知得 , 解得 所以函数 的定义域为
(2) ,令
,得 ,即 ,解得 ,∵ ,∴
函数 的零点是
(3)由2知, ,
∵ ,∴ .
∵ ,∴ ,
∴ ,
∴ .
22.(本小题12分)
十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在
大力实施一项将重塑全球汽车行业的计划.2018年某企业计划引进新能源汽车生产设备,
通过市场分析,全年需投入固定成本2500万元,每生产x(百辆),需另投入成本
万元,且 .由市场调研知,每辆车售价5
万元,且全年内生产的车辆当年能全部销售完.
(1)求出2018年的利润L(x)(万元)关于年产量x(百辆)的函数关系式;(利润=
销售额-成本)
- 12 -(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
【答案】(1) ;(2)生产100百辆时,该
企业获得利润最大,且最大利润为1800万元.
【解析】
(1)当 时,
;
当 时, ;
∴ .
(2)当 时, ,
∴当 时, ;
当 时, ,
当且仅当 ,即 时, ;
∴当 时,即2018年生产100百辆时,该企业获得利润最大,且最大利润为1800
万元.