河池十校联体2024-10月考高一数学答案_2024-2025高一（7-7月题库）_2024年11月试卷_1107广西河池十校高一联考2024-2025学年10月考

2024 年秋季学期高一年级校联体第一次联考 数学参考答案 1.【答案】C 【详解】由全称命题的否定可知，命题“xR， x x2 1”的否定是“x R， x x2 1”. 0 0 0 故选：C. 2.【答案】B 【详解】因为B x|2x2 ，故AB1,1  ，故选：B. 3.【答案】C 1 x30 【详解】函数 f(x) x3 有意义，则 ，解得x3， 1x 1x0 所以原函数的定义域为[3,). 故选：C. 4.【答案】D 【详解】因为A0,1，所以集合A有,0,1,0,1共4个子集. 故选：D. 5.【答案】B 1x (1x)(1x)0 【详解】不等式 0等价于 ，解之得1x<1. 1x  1x0 故选：B. 6.【答案】A 【详解】 f x为奇函数可以推出 f 00， 但是 f 00推不出 f x为奇函数， 因此“ f 00”是“ f x是定义在R上的奇函数”的必要不充分条件. 故选：A. 7.【答案】A m 【详解】因为 在,2 上单调递减，所以对称轴 2，即m4. 2 故选：A. ( ) 8.【答案】B 【详解】解：由题意可知a0时，不等式显然不恒成立， 所以当a0，由不等式ax2xa0对所有的实数x都成立， a0 1 可得 ，解得a . 0 2 故选：B． 9.【答案】AD 1 【详解】函数yx2是非奇非偶函数，yx 是(,0)(0,)上的奇函数，BC不是； x 函数yx22，y x 1均为偶函数.又二次函数y x2 2在0,上为单调递增. y x 1，当x0时，函数可化为yx1，在0,上为单调递增，AD正确. 故选：AD. 10.【答案】BC 【详解】对于A：若c0，则ac2 bc2 0，故A错误； 数学参考答案 第1 页 共4页 学习资料，无偿分享 {#{QQABaQCEggCoABAAAQgCQQliCEOQkhACAQgOwAAEMAAACBFABAA=}#}对于B：若ab4，则a2b2 2ab8，当且仅当ab2时，等号成立，故B正确； 对于C：若ab,cd ，则d c，所以ad bc，故C正确； 1 1 对于D：当b  a  0时，则  ，故D错误. b a 故选：BC. 11.【答案】ACD 【详解】对于A项，分式中分母不等于0，所以x10，解得：x1. 所以 f x的定义域是,1  1,；故A项正确； 对于B项，多个单调区间可用逗号（或“和”）隔开，所以 f x在,1，1,上单调递减，在 ,1  1,上不是单调递减的，故B项错误； 2 2 2 对于C项， f x1 ，令g(x) ，定义域为(,0)(0,)，g(x) g(x) 所以g(x)是奇函数， x x x 即 f x1是奇函数，故C项正确； 对于D项， f x的值域是(,0)(0,)，故D项正确. 故选：ACD. 12.【答案】1 【详解】 f  2   2  6  6   1 ， f  f  2   f 1 1 2 1. 2 故答案为：1. 13.【答案】 2 【详解】函数y x2 2x3的图象是开口向上，且以直线x  1 为对称轴的抛物线， 当x1,3时，y x2 2x3单调递增，在x1时取得最小值2. 故答案为：2. 14．【答案】6 ab 2 ab 2 【详解】a,b0,ab  ，ab3   2   2  ab2 4(ab)120,  (ab)6  (ab)2 0, ab60,ab6,当且仅当ab时，等式成立 即ab最小值为6 故答案为:6 15.【答案】(1)由Ax|x4,Bx|6x6得ABx|4 x6,················4分 ABx|x6 ······················································································4分（8分） (2)由Bx|6x6得C B={x|x＜－6或x＞6},··········································2分 U 故A∩(C B)={x|x＞6}···················································································3分（13分） U 16.【答案】（1）∵x1，即x10，·······························································1分 1 1 1 4x 4x1 42 4x1 4448，·····························3分 x1 x1 x1 1 3 当且仅当 4x1，即 x  时取等号，··················································2分 x1 2 1 ∴4x 的最小值为8．············································································1分（7分） x1 （2）由题可得B是A的真子集，·······································································1分 当B，则m12m1m2；························································· 2分（10分） 数学参考答案 第2 页 共4页 学习资料，无偿分享 {#{QQABaQCEggCoABAAAQgCQQliCEOQkhACAQgOwAAEMAAACBFABAA=}#}2m17 当B，m≥2，则 （等号不同时成立），解得2m4；·············3分 m12 综上，m4.··························································································2分（15分） 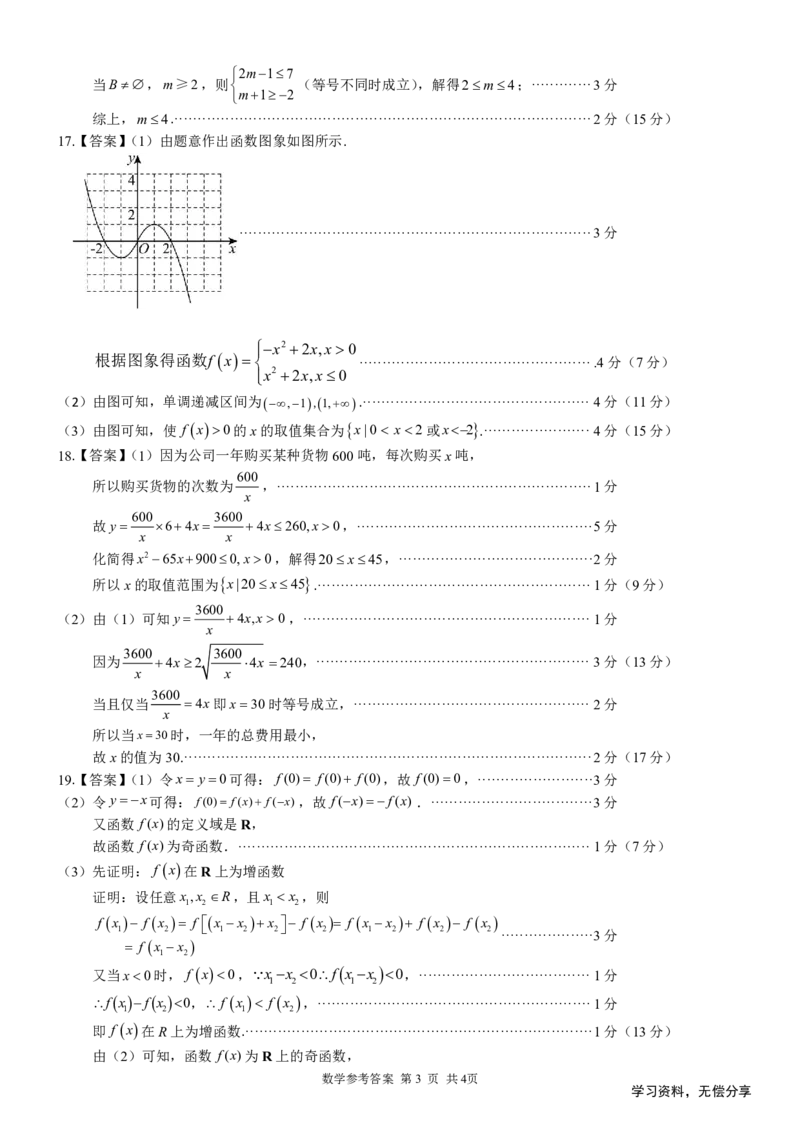17.【答案】（1）由题意作出函数图象如图所示. ············································································3分 x2 2x,x0 根据图象得函数f  x  ··················································.4分（7分） x2 2x,x0 （2）由图可知，单调递减区间为,1,1,.················································· 4分（11分） （3）由图可知，使 f x0的x的取值集合为x|0 x 2或x2 .·······················4分（15分） 18.【答案】（1）因为公司一年购买某种货物600吨，每次购买x吨， 600 所以购买货物的次数为 ，····································································1分 x 600 3600 故y 64x 4x260,x0，···················································5分 x x 化简得x265x9000,x0，解得20x45，··········································2分 所以x的取值范围为x|20x45 .···························································1分（9分） 3600 （2）由（1）可知y 4x,x0，······························································1分 x 3600 3600 因为 4x2 4x 240，··························································· 3分（13分） x x 3600 当且仅当 4x即x30时等号成立，···················································2分 x 所以当x30时，一年的总费用最小， 故x的值为30.························································································2分（17分） 19.【答案】（1）令x y0可得： f(0) f(0) f(0)，故 f(0)0，·························3分 （2）令yx可得： f(0) f(x) f(x)，故 f(x)f(x) ．···································3分 又函数 f(x)的定义域是R， 故函数 f(x)为奇函数．············································································1分（7分） （3）先证明： f x在R上为增函数 证明：设任意x,x R，且x x ，则 1 2 1 2 f x 1  f x 2  f   x 1 x 2 x 2    f x 2  f x 1 x 2  f x 2  f x 2  ····················3分  f x x  1 2 又当x0时， f x0，x x 0f  x x 0，·····································1分 1 2 1 2 fxfx 0，f x  f x ，···························································1分 1 2 1 2 即 f x在R上为增函数.···········································································1分（13分） 由（2）可知，函数 f(x)为R上的奇函数， 数学参考答案 第3 页 共4页 学习资料，无偿分享 {#{QQABaQCEggCoABAAAQgCQQliCEOQkhACAQgOwAAEMAAACBFABAA=}#}因为 f(x2) f  x22x  0． 所以 f(x2)f  x22x   f  2xx2 ．····················································1分 所以x22xx2，················································································1分 解得x1或x2,·················································································1分 故 x x1或x2  ··················································································1分（17分） 数学参考答案 第4 页 共4页 学习资料，无偿分享 {#{QQABaQCEggCoABAAAQgCQQliCEOQkhACAQgOwAAEMAAACBFABAA=}#}