文档内容
2024-2025 学年浙江省台州市高一上学期 1 月期末质量评估数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若幂函数 经过点 ,则 ( )
f(x)=xα (2,√2) f(9)=
1 1
A. 81 B. C. 3 D.
81 3
2.已知函数y=f(x)在区间[0,3]上的图象是一条连续不断的曲线,且f(0)=−1.1,f(1)=2,f(2)=1.5,
f(3)=−2.35,则函数y=f(x)在区间[0,3]上的零点至少有( )
A. 1个 B. 2个 C. 3个 D. 4个
3.“x>1,y>2”是“x+ y>3”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4.已知扇形的圆心角为1rad,面积为8,则扇形的弧长为( )
A. 8 B. 4 C. 8π D. 4π
5.若α∈(0,π),2sinα+cosα=1,则tanα=( )
4 5 3 4
A. − B. − C. − D. −
5 4 4 3
π
6.将函数f(x)=sin2x的图象向左平移φ(0<φ≤ )个单位,得到的函数图象关于y轴对称,则φ的值为
2
( )
π π π π
A. B. C. D.
6 4 3 2
7.设a=log 4,b=log 6,c=log 6,则( )
6 8 9
A. a>c>b B. b>a>c C. b>c>a D. c>b>a
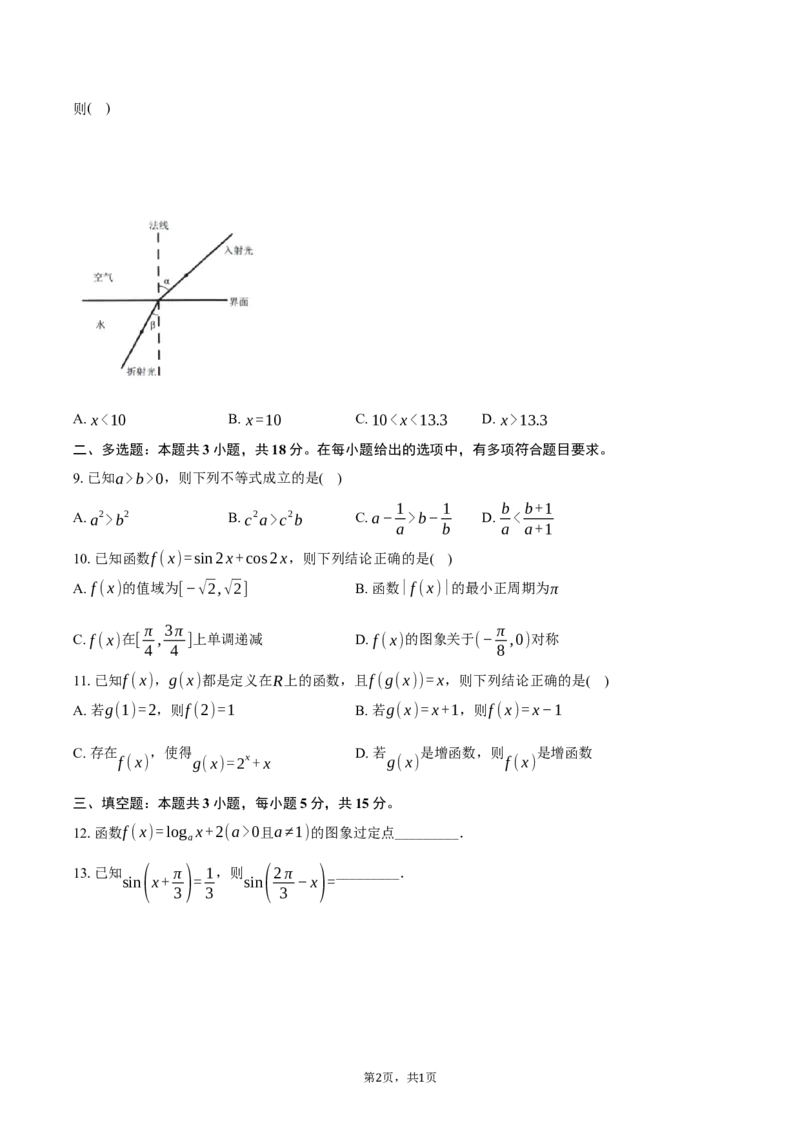
8.光从一种介质斜射入另一种介质时,传播方向通常会发生改变,这种现象称为光的折射.光在折射过程中,
入射角的正弦值与折射角的正弦值的比值是一个常数.例如,一束光线从空气斜射入水时,会发生折射现象,
sinα
并满足 =1.33(其中α是入射角,β是折射角).当入射角α(0∘<α<80∘)增加10∘时,折射角β增加x∘,
sinβ
第 页,共 页
1 1则( )
A. x<10 B. x=10 C. 1013.3
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知a>b>0,则下列不等式成立的是( )
1 1 b b+1
A. a2>b2 B. c2a>c2b C. a− >b− D. <
a b a a+1
10.已知函数f(x)=sin2x+cos2x,则下列结论正确的是( )
A. f(x)的值域为[−√2,√2] B. 函数|f(x)|的最小正周期为π
π 3π π
C. f(x)在[ , ]上单调递减 D. f(x)的图象关于(− ,0)对称
4 4 8
11.已知f(x),g(x)都是定义在R上的函数,且f(g(x))=x,则下列结论正确的是( )
A. 若g(1)=2,则f(2)=1 B. 若g(x)=x+1,则f(x)=x−1
C. 存在 ,使得 D. 若 是增函数,则 是增函数
f(x) g(x)=2x+x g(x) f(x)
三、填空题:本题共3小题,每小题5分,共15分。
12.函数f(x)=log x+2(a>0且a≠1)的图象过定点_________.
a
13.已知 ( π) 1,则 (2π ) _________.
sin x+ = sin −x =
3 3 3
第 页,共 页
2 114.某工厂产生的废气经过滤后排放,过滤过程中废气的污染物含量P(单位:mg/L)与时间t(单位:ℎ)
间的关系为 ,其中 , 是正常数.污染物的初始含量为 ;如果在前 消除了
P=P
0
e−kt P
0
k mg/L 5ℎ
10%的污染物,那么污染物减少70%需要花费 小时(精确到1ℎ).(参考数据:lg3≈0.477)
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
求值:
1 2
27
(1)492+( )3−2−2+√3 (π−2) 3;
8
√1+2sin20∘sin70∘
.
(2)
sin70∘+√1−cos2160∘
16.(本小题12分)
已知集合 ,
A={x|x2−(2+a)x+2a<0} B={x|y=√−x2−2x+3}.
(1)若a=0时,求(∁ A)∩B;
R
(2)若A∪B=A,求实数a的取值范围.
17.(本小题12分)
已知函数
2x+1
是奇函数.
f(x)= +a
2x+1
(1)求a的值,判断函数f(x)的单调性并请说明理由;
对任意 ,不等式 恒成立,求实数 的取值范围.
(2) x∈R f(k⋅2x )+f(3⋅2x−4x−1)≤0 k
18.(本小题12分)
已知O(0,0),A(cosα,sinα),B(cosβ,sinβ),α≠β+2kπ,k∈Z.
(1)请写出以x轴的非负半轴为始边,射线OA为终边的角的集合;
(2)作点A关于直线OB的对称点C(cosγ,sinγ).
π π
①当α= ,β= 时,求点C坐标;
4 3
√21 √15 1
②若B( , ),cosαcosγ= ,求cos(α−γ).
6 6 4
19.(本小题12分)
第 页,共 页
3 1给定函数f(x),若对任意一个三角形,只要它的三边长a,b,c都在f(x)的定义域内,就有f(a),f(b),
f(c)也是某个三角形的三边长,则称f(x)为“保三角形函数”.
(1)判断函数g(x)=3x是否为“保三角形函数”,并说明理由;
(2)若ℎ(x)=ln(x+m)是“保三角形函数”,求m的最小值;
(3)若函数p(x)同时满足以下条件:
①p(0)=0;
②p(x)在区间(0,+∞)上单调递增;
③对任意x ,x ∈[0,+∞),λ∈[0,1]都有p(λx +(1−λ)x )≥λp(x )+(1−λ)p(x ).
1 2 1 2 1 2
证明:函数p(x)是“保三角形函数”.
第 页,共 页
4 1参考答案
1.C
2.B
3.A
4.B
5.D
6.B
7.C
8.A
9.ACD
10.AD
11.ABD
12.(1,2)
1
13.
3
14.P ;57
0
15.解:
9 1
(1)原式=7+ − +π−2=7+π;
4 4
原式
√1+2sin20°cos20∘ sin20∘+cos20∘ sin20∘+cos20∘ sin20∘+cos20∘
.
(2) = == = = =1
sin70∘+√1−cos2160∘ sin70∘+sin160∘ sin70∘+sin20∘ cos20∘+sin20∘
16.解: , 或 , .
(1)A={x|02时,A={x|20
1 2
所以f(x )−f(x )<0,即f(x )c.
此时g(a)=3a>0,g(b)=3b>0,g(c)=3c>0,
且有g(a)+g(b)=3a+3b=3(a+b)>3c=g(c),
所以g(a),g(b),g(c)可以构成某三角形的三边.
所以g(x)=3x是“保三角形函数”.
(2)因为ℎ(x)=ln(x+m)是“保三角形函数”,所以a>0,b>0,c>0且ℎ(a)>0,ℎ(b)>0,ℎ(c)>0,
必有ln(x+m)>0对∀x>0恒成立,
所以lnm≥0,解得m≥1.
下证:当m≥1时,ℎ(x)=ln(x+m)是“保三角形函数”.
不妨设0c.
第 页,共 页
7 1此时ℎ(a)=ln(a+m)>0,ℎ(b)=ln(b+m)>0,ℎ(c)=ln(c+m)>0,
ℎ(a)+ ℎ(b)=ln(a+m)+ln(b+m)=ln[(a+m)(b+m)]=ln[ab+(a+b)m+m2 ]≥ln(ab+a+b+m)>ln(c+m)= ℎ(c)
所以若ℎ(x)=ln(x+m)是“保三角形函数”,m的最小值为1.
(3)不妨设0c.
p(a)>0,p(b)>0,p(c)>0.
由p(λx +(1−λ)x )≥λp(x )+(1−λ)p(x ),λ∈[0,1],
1 2 1 2
知当x =0时,p(λx )≥λp(x ).
2 1 1
a a
所以p(a)=p( (a+b))≥ p(a+b),
a+b a+b
b b
p(b)=p( (a+b))≥ p(a+b).
a+b a+b
a b
所以p(a)+p(b)≥ p(a+b)+ p(a+b)=p(a+b).
a+b a+b
而a+b>c,p(x)在区间(0,+∞)上单调递增,
所以p(a+b)>p(c).
所以p(a)+p(b)>p(c),即函数p(x)是“保三角形函数”.
第 页,共 页
8 1