文档内容
第七章 随机变量及其分布(基础卷)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分150分,考试时间1200分钟,试题共23题.答卷前,考生务必用0.5毫米黑色签字笔将
自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共12小题,每小题5分,共60分)在每小题所给出的四个选项中,只有一项是符合
题目要求的.
1.已知某离散型随机变量X服从的分布列如图,则随机变量X的方差D(X)等于( )
X 0 1
P m 2m
A. B. C. D.
【答案】B
【分析】由于已知分布列即可求出m的取值,进而使用公式求期望、方差.
【解答】解:由题意可得:m+2m=1,所以m= ,
所以E =0× +1× = ,
所以D =(0﹣ )2× +(1﹣ )2× = .
ξ
故选:B.
ξ
【知识点】离散型随机变量的期望与方差
2.将三颗骰子各掷一次,设事件A=“三个点数都不同”,B=“至少出现一个3点”,则条件概率P(A|
B),P(B|A)分别是( )
A. , B. , C. , D. ,
【答案】A
【分析】根据条件概率的含义,明确条件概率P(A|B),P(B|A)的意义,即可得出结论.
【解答】解:根据条件概率的含义,P(A|B)其含义为在B发生的情况下,A发生的概率,即在“至少出
现一个3点”的情况下,“三个点数都不相同”的概率,
∵“至少出现一个3点”的情况数目为6×6×6﹣5×5×5=91,“三个点数都不相同”则只有一
个3点,共 ×5×4=60种,∴P(A|B)= ;
P(B|A)其含义为在A发生的情况下,B发生的概率,即在“三个点数都不相同”的情况下,
“至少出现一个3点”的概率,∴P(B|A)=
故选:A.
【知识点】条件概率与独立事件
3.随机变量X的概率分布规律为P(X=n)= (n=1,2,3,4),其中a是常数,则P( <X< )的
值为( )
A. B. C. D.
【答案】D
【分析】根据所给的概率分步规律,写出四个变量对应的概率,根据分布列的性质,写出四个概率之和是
1,解出a的值,要求的变量的概率包括两个变量的概率,相加得到结果.【解答】解:∵P(X=n)= (n=1,2,3,4),
∴ + + + =1,
∴a= ,
∵P( <X< )=P(X=1)+P(X=2)= × + × = .
故选:D.
【知识点】离散型随机变量及其分布列
4.已知离散型随机变量X服从二项分布X~B(n,p)且E(X)=12,D(X)=4,则n与p的值分别为
( )
A. B. C. D.
【答案】A
【分析】根据随机变量符合二项分布,由二项分布的期望和方差的公式,及条件中所给的期望和方差的值,
列出期望和方差的关系式,得到关于n和p的方程组,解方程组可得到n,p的值.
【解答】解:∵随机变量X服从二项分布X~B(n,p),且E(X)=12,D(X)=4,
∴E(X)=12=np,①
D(X)=4=np(1﹣p),②
①与②相除可得1﹣p= ,
∴p= ,n=18.
故选:A.
【知识点】二项分布与n次独立重复试验的模型
5.体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球,否则一
直发到3次为止.设学生一次发球成功的概率为 p (p≠0),发球次数为X,若X的数学期望EX>
1.75,则p的取值范围是( )
A.(0, ) B.( ,1) C.(0, ) D.( ,1)
【答案】C
【分析】根据题意,首先求出X=1、2、3时的概率,进而可得EX的表达式,由题意EX>1.75,可得p2
﹣3p+3>1.75,解可得p的范围,结合p的实际意义,对求得的范围可得答案.
【解答】解:根据题意,学生发球次数为1即一次发球成功的概率为p,即P(X=1)=p,
发球次数为2即二次发球成功的概率P(X=2)=p(1﹣p),
发球次数为3的概率P(X=3)=(1﹣p)2,
则Ex=p+2p(1﹣p)+3(1﹣p)2=p2﹣3p+3,
依题意有EX>1.75,则p2﹣3p+3>1.75,
解可得,p> 或p< ,
结合p的实际意义,可得0<p< ,即p (0, )
故选:C.
∈
【知识点】离散型随机变量的期望与方差、相互独立事件和相互独立事件的概率乘法公式
6.设随机变量 ﹣N( ,1),若不等式 ≥0对任意实数x都成立,且P( >a)= ,则 的值为
( ) ξ μ ξ μ
A.0 B.1 C.2 D.3
【答案】A
【分析】根据所给的不等式恒成立,把不等式整理成分离参数以后的结果,把a单独整理出来,根据幂函数的性质,写出不等式右边的取值范围,得到a的值,根据符合正态分布和正态分布的性质,得
到结果.
【解答】解:∵不等式x2﹣ ≥0对任意实数x都成立,
∴x2≥ ,
∴a≤ ,
∵ ∈[0,+∞),
∴在四个选项中a只能取0,
∴a=0,
∵随机变量 ~N( ,1),且P( >a)= ,
∴ =0,
ξ μ ξ
故选:A.
μ
【知识点】函数恒成立问题、连续型随机变量
7.已知某批零件的长度误差(单位:毫米)服从正态分布N(0,32),从中随机抽取一件,其长度误差落
在区间(3,6)内的概率为( )
(附:若随机变量 服从正态分布N( ,σ2),则P( ﹣σ< < +σ)=68.26%,P( ﹣2σ< < +2σ)
=95.44%) ξ μ μ ξ μ μ ξ μ
A.4.56% B.13.59% C.27.18% D.31.74%
【答案】B
【分析】由题意P(﹣3< <3)=68.26%,P(﹣6< <6)=95.44%,可得P(3< <6)= (95.44%﹣
68.26%),即可得出结论.
ξ ξ ξ
【解答】解:由题意P(﹣3< <3)=68.26%,P(﹣6< <6)=95.44%,
所以P(3< <6)= (95.44%﹣68.26%)=13.59%.
ξ ξ
故选:B.
ξ
【知识点】正态分布曲线的特点及曲线所表示的意义
8.若随机变量X~N( ,σ2)(σ>0),则有如下结论:
高三(1)班有40名同μ 学,一次数学考试的成绩服从正态分布,平均分为120,方差为100,理论上说在
130分以上人数约为( )
A.19 B.12 C.6 D.5
【答案】C
【分析】正态总体的取值关于x=120对称,在130分的概率为 (1﹣0.6826)=0.1587,得到要求的结果.
【解答】解:∵数学成绩近似地服从正态分布N(120,102),
P(|x﹣u|<σ)=0.6826,
∴P(|x﹣120|<10)=0.6826,
根据正态曲线的对称性知:理论上说在130分的概率为 (1﹣0.6826)=0.1587
∴理论上说在130分以上人数约为0.1587×40≈6.
故选:C.
【知识点】正态分布曲线的特点及曲线所表示的意义
9.设离散型随机变量X的分布列为
X 1 2 3P P P P
1 2 3
则EX=2的充要条件是( )
A.P=P B.P=P C.P=P D.P=P=P
1 2 2 3 1 3 1 2 3
【答案】C
【分析】当 EX=2 时,由离散型随机变量 X 的分布列的性质列出方程组得 P=P ,当 P=P 时,
1 3 1 3
P+P+P=2P+P=1能求出EX=2.从而得到EX=2的充要条件是P=P.
1 2 3 1 2 1 3
【解答】解:由离散型随机变量X的分布列知:
当EX=2时, ,解得P=P,
1 3
当P=P 时,P+P+P=2P+P=1.
1 3 1 2 3 1 2
EX=P+2P+3P=4P+2P=2.
1 2 3 1 2
∴EX=2的充要条件是P=P.
1 3
故选:C.
【知识点】离散型随机变量及其分布列
10.口袋里放有大小相等的2个白球和1个红球,有放回地每次摸取1个球,定义数列{a}:a =
n n
如果S 为数列{a}的前n项和,那么S=5的概率为( )
n n 7
A. B.
C. D.
【答案】A
【分析】直接利用独立重复试验的关系式的应用求出结果.
【解答】解:口袋里放有大小相等的2个白球和1个红球,有放回地每次摸取1个球,
则摸出红球的概率为 ,摸出白球的概率为 .
由于定义数列{a}:a=
n n
如果S 为数列{a}的前n项和,那么S=5相当于摸了7次球,摸出6次白球,一次红球,
n n 7
所以根据独立重复试验概率为 .
故选:A.
【知识点】n次独立重复试验中恰好发生k次的概率
11.盒中有6个小球,其中4个白球,2个黑球,从中任取i(i=1,2)个球,在取出的球中,黑球放回,
白球则涂黑后放回,此时盒中黑球的个数X(i=1,2),则( )
i
A.P(X=3)>P(X=3),EX>EX
1 2 1 2
B.P(X=3)<P(X=3),EX>EX
1 2 1 2
C.P(X=3)>P(X=3),EX<EX
1 2 1 2
D.P(X=3)<P(X=3),EX<EX
1 2 1 2
【答案】C
【分析】根据古典概型概率公式求得概率,期望,比较可得.
【解答】解:X=3表示取出的为一个白球,∴P(X=3)= = ,X=2表示取出一个黑球,P(X=2)
1 1 1 1
= = ,E(X)=3× +2× = ;
1
X =3表示取出两个球,其中一黑一白,P(X =3)= = ;X =2表示取出2个球为黑球,
2 2 2
P(X )= = ,X =4表示取出2个白球,P(X =4)= = ,E(X )=3× +2× +4× = =
2 2 2 2
,故选:C.
【知识点】离散型随机变量的期望与方差
12.我们知道,在n次独立重复试验(即伯努利试验)中,每次试验中事件A发生的概率为p,则事件A发
生的次数X服从二项分布B(n,p),事实上,在无限次伯努利试验中,另一个随机变量的实际应用也
很广泛,即事件A首次发生时试验进行的次数Y,显然P(Y=k)=p(1﹣p)k﹣1,k=1,2,3,…,
我们称Y服从“几何分布”,经计算得 .由此推广,在无限次伯努利试验中,试验进行到事件A和
都发生后停止,此时所进行的试验次数记为Z,则P(Z=k)=p(1﹣p)k﹣1+(1﹣p)pk﹣1,k═2,
3,…,那么E(Z)=( )
A. B. C. D.
【答案】A
【分析】P(Z=k)=p(1﹣p)k﹣1+(1﹣p)pk﹣1,k═2,3,…,P(Y=k)=p(1﹣p)k﹣1,k=1,2,
3,…,可得 .于是P(Y=k)=p(1﹣p)k﹣1,k=2,3,…, ﹣p.而E(Z)=2p(1﹣
p)+2(1﹣p)p+3p(1﹣p)2+3(1﹣p)p2+……+kp(1﹣p)k﹣1+k(1﹣p)pk﹣1+….= ﹣p+2
(1﹣p)p+3(1﹣p)p2+……+k(1﹣p)pk﹣1+….设A=2p+3p2+……+kpk﹣1.利用错位相减法
k
即可得出A.
k
【解答】解:P(Z=k)=p(1﹣p)k﹣1+(1﹣p)pk﹣1,k═2,3,…,P(Y=k)=p(1﹣p)k﹣1,k=1,
2,3,…,可得 .
∴P(Y=k)=p(1﹣p)k﹣1,k=2,3,…, ﹣p.
那么E(Z)=2p(1﹣p)+2(1﹣p)p+3p(1﹣p)2+3(1﹣p)p2+……+kp(1﹣p)k﹣1+k(1
﹣p)pk﹣1+…
= ﹣p+2(1﹣p)p+3(1﹣p)p2+……+k(1﹣p)pk﹣1+….
设A=2p+3p2+……+kpk﹣1.
k
pA=2p2+3p3+……+(k﹣1)pk﹣1+kpk.
k
∴(1﹣p)A=2p+p2+p3+……+pk﹣1﹣kpk=p+ ﹣kpk.
k
∴k→+∞时,(1﹣p)A→p+ .
k
∴E(Z)= ﹣p+p+ = ﹣1.
故选:A.
【知识点】二项分布与n次独立重复试验的模型
二、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线
上)
13.某地区空气质量监测资料表明,一天的空气质量为优良的概率是 ,连续两天为优良的概率是 ,已知某
天的空气质量为优良,则随后一天的空气质量为优良的概率是 .
【分析】设随后一天的空气质量为优良的概率为p,则由题意可得 ×p= ,由此解得p的值.
【解答】解:设随后一天的空气质量为优良的概率为p,则由题意可得 ×p= ,
解得p= ,
故答案为: .
【知识点】条件概率与独立事件14.下列随机变量中,不是离散型随机变量的是 .
①某地车展中,预定各类汽车的总人数X;
②北京故宫某周每天接待的游客人数;
③正弦曲线上的点P到x轴的距离X ;
④小麦的亩产量X;
⑤王老师在一次英语课上提问的学生人数X.
【答案】①④⑤
【分析】根据离散型随机变量的定义:其可能取到的不相同的值是有限个或可列为有限个,分析题干的变
量可得结论.
【解答】解:根据离散型随机变量的定义:其可能取到的不相同的值是有限个或可列为有限个,即可以按
一定次序一一列出;
分析题干的变量可得
①某地车展中,预定各类汽车的总人数X,符合定义,是离散型随机变量;
②北京故宫某周每天接待的游客人数,不符合定义,不是离散型随机变量;
③正弦曲线上的点P到x轴的距离X,无法按一定次序一一列出,不符合定义,不是离散型随
机变量;
④小麦的亩产量X,符合定义,是离散型随机变量;
⑤王老师在一次英语课上提问的学生人数X,符合定义,是离散型随机变量.
故答案为:①④⑤.
【知识点】连续型随机变量
15.已知随机变量 的分布列为:
ξ ﹣1 0 1 2
Pξ ﹣2a b
若 ,则a+b= ,D( )= .
ξ
【分析】由E( )= ,利用随机变量 的分布列,列出方程组求出a=﹣ ,b= ,由此能求出a+b和D
( ).
ξ ξ
【解答】解:∵ ,
ξ
∴由随机变量 的分布列,得:2a+ +2b= ,并且﹣2a+ +b=1,
解得a= ,b= ,a+b= ,
ξ
∴D( )= ×(﹣1﹣ )2+ (0﹣ )2+ ×(1﹣ )2+ ×(2﹣ )2= .
故答案为: ; .
ξ
【知识点】离散型随机变量的期望与方差
16.甲、乙两名同学参加一项射击比赛游戏,其中任何一人射击一次击中目标得2分,未击中目标得0分.
若甲、乙两人射击的命中率分别为 和p,且甲、乙两人各射击一次得分之和为2的概率为 .假设甲、
乙两人射击互不影响,则p的值为 .
【分析】利用相互独立事件概率乘法公式直接求解.【解答】解:甲、乙两名同学参加一项射击比赛游戏,其中任何一人射击一次击中目标得2分,未击中目
标得0分.
甲、乙两人射击的命中率分别为 和p,且甲、乙两人各射击一次得分之和为2的概率为 .
假设甲、乙两人射击互不影响,
则P= = ,
解得p= .
故答案为: .
【知识点】相互独立事件和相互独立事件的概率乘法公式
三、解答题(本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过
程或演算步骤)
17.一袋中有6个黑球,4个白球.
(1)依次取出3个球,不放回,已知第一次取出的是白球,求第三次取到黑球的概率;
(2)有放回地依次取出3球,已知第一次取的是白球,求第三次取到黑球的概率;
(3)有放回地依次取出3球,求取到白球个数X的分布列.
【分析】(1)由题意知在第一次取出的是白球时,求第三次取到黑球的概率,这是一个条件概率,先做
出第一次取到白球的结果数,再做出第一次取到白球且第三次取到黑球的结果数,根据条件概率
的公式得到结果.
(2)有放回地依次取出3球,第一次取的是白球,第三次取到黑球,这两个事件没有关系,
只要做出从10个球中摸一个球,摸到黑球的概率就可以.
(3)取到白球个数X,由题意知X的可能取值是0,1,2,3,做出一次取到白球的概率,利
用独立重复试验的概率公式写出变量对应的概率,写出分布列.
【解答】解:(1)设A=“第一次取到白球”,
B=“第二次取到白球”,C=“第三次取到白球”,
则在A发生的条件下,袋中只剩6个黑球和3个白球,
则P(|A)= = = .
(2)∵每次取之前袋中球的情况不变,
∴n次取球的结果互不影响.
∴P()= = .
(3)取到白球个数X,由题意知X的可能取值是0,1,2,3
设“摸一次球,摸到白球”为事件D,
则P(D)= = ,P()= .
∵这三次摸球互不影响,
∴P(X=0)=C0( )3,P(X=1)=C1( )( )2,
3 3
P(X=2)=C2( )2( ),P(X=3)=C3( )3.
3 3
∴X的分布列为:
【知识点】等可能事件和等可能事件的概率、二项分布与n次独立重复试验的模型、离散型随机变量的期望与方差、条件概率与独立事件
18.某中学随机抽取部分高一学生调查其每日自主安排学习的时间(单位:分钟),并将所得数据绘制成
如图所示的频率分布直方图,其中自主安排学习时间的范围是[0,100],样本数据分组为[0,20),
[20,40),[40,60),[60,80),[80,100].
(Ⅰ)求直方图中x的值;
(Ⅱ)从学校全体高一学生中任选4名学生,这4名学生中自主安排学习时间少于20分钟的人数记为X,
求X的分布列和数学期望.(以直方图中的频率作为概率).
【分析】(Ⅰ)利用直方图概率的和为1,直接求解x即可.
(Ⅱ)依题意得 ~B(4, ), 的所有可能取值为0,1,2,3,4,由此能求出 的分布列
及其数学期望.
ξ ξ ξ
【解答】解:(Ⅰ)20×(x+0.025+0.0065+0.003+0.0003)=1,
得x=0.0125.
(Ⅱ)X的可能取值为:0,1,2,3,4,且X~B(4, ),
P(X=0)= = ,同理可得下表:
X 0 1 2 3 4
P
所以,E(X)=1.
【知识点】离散型随机变量及其分布列、频率分布直方图、离散型随机变量的期望与方差
19.设从某地前往火车站,可乘公共汽车,也可乘地铁,若乘公共汽车所需时间(单位:min)X~N(50,
102),乘地铁所需时间Y~N(60,42),则
(1)若有70min可用,则乘公共汽车好还是乘地铁好?
(2)由于时间紧迫,决定做出租车去火车站,此时使用手机中打车软件甲,甲软件定位了 A公司2辆出
租车,B公司4辆出租车,每车被叫中的概率相等,甲软件能叫来两辆车,求A公司出租车被叫来的辆数
的分布列和数学期望 E( ).(已知 P( ﹣3σ<X≤ +3σ)=0.9974,P( ﹣2σ<X≤ +2σ)=
ɛ0.9544) ɛ μ μ μ μ
【分析】(Ⅰ)先设行车时间为 .分别利用所需时间服从正态分布计算出走第一条路线及时赶到的概率
和走第二条路线及时赶到的概率后,比较大小即可;
ξ
(Ⅱ) 的取值为0,1,2,求出相应的概率,即可求出A公司出租车被叫来的辆数 的分布
列和数学期望E( ).
ɛ ɛ
【解答】解:设行车时间为 .
ɛ
ξ(1)走第一条路线及时赶到的概率为 P(0< ≤70)= ( )﹣ ( )= (2)﹣
((﹣5)≈0.9772.
ξ Φ Φ Φ Φ
走第二条路线及时赶到的概率为P(0< ≤70)= ( )≈0.9938.
因此在这种情况下应走第二条路线.
ξ Φ
(2) 的取值为0,1,2.则
P( =0)= = ,P( =1)= = ,P( =2)= = ,
ɛ
的分布列
ɛ ɛ ɛ
0 1 2
ɛ
ɛP
E =0× +1× +2× = .
【知识点】正态分布曲线的特点及曲线所表示的意义
ɛ
20.甲、乙两人射击,甲射击一次中靶的概率是p,乙射击一次中靶的概率是p,且 , 是方程x2﹣5x+6=
1 2
0的两个实根,已知甲射击5次,中靶次数的方差是 .
(1)求p,p 的值;
1 2
(2)若两人各射击2次,至少中靶3次就算完成目的,则完成目的概率是多少?
(3)若两人各射击1次,至少中靶1次就算完成目的,则完成目的概率是多少?
【分析】(1)甲射击5次,中靶次数k服从二项分布,根据二项分布的方差计算公式D =5p (1﹣
甲 1
p),即可求得p,根据韦达定理得 =6,可求得p 的值;
1 1 2
ξ
(2)两人各射击2次,中靶至少3次就算完成目的,分两种情况讨论,共击中3次的概率,
根据n次独立重复实验事件A恰好发生k的概率公式,代入即可求得结果;同理可求出击中4
次的概率,这两种情况互斥,根据概率的加法公式即可求得结果;
(3)两人各射击一次,中靶至少一次就算完成目的,该事件的对立事件为“两人各射击一次,
没有中靶”,利用对立事件的概率公式即可求得结果.
【解答】解:(1)由题意可知 ~B(5,p),
甲 1
∴D =5p (1﹣p)= ,
甲 1 1
ξ
∴p2﹣p+ =0,
1 1
ξ
解得p= ;
1
又 , 是方程x2﹣5x+6=0的两个实根,
∴ =6,
解得p= .
2
(2)两人各射击2次,至少中靶3次就算完成目的,则完成目的两类情况:
①共击中3次概率C 2( ) 2 (1﹣ )×C 1( ) 1 (1﹣ ) 1+C 1( ) 1 ( ) 1×C 2( ) 2
2 2 2 2
( )= ;
共击中4次概率C 2( ) 2 ( )×C 2( ) 2 ( )= .
2 2
∴所求概率为 = .
(3)设事件A,B分别表示甲、乙能击中.
∵A,B互相独立,
∴P(• )=P() P()=(1﹣P(A) )(1﹣P(B) )=(1﹣p)(1﹣p)= ,
1 2
∴“两人各射击一次,中靶至少一次就算完成目的”的概率为:1﹣P(•)= .
【知识点】相互独立事件和相互独立事件的概率乘法公式
21.某省高考曾经使用过一段标准分制度,标准分是把学生考试的基础分参与全省排出相对名称,通过公式换算成标准分.高考后公布考生的标准分,而不公布基础分.考生根据自己的标准分多少就可以大
致估出自己在全省考生的名次.其标准分X是服从正态分布N(500,1002)的随机变量.假设某学生
的数学成绩不低于600的概率为p.
0
(Ⅰ)求p 的值;
0
(Ⅱ)某校高三的高考英语和数学两科都超过600分的有5人,仅单科超过600分的共有8人,在这些同
学中随机抽取3人,设三人中英语和数学双科都超过600分的有 人,求 的分布列和数学期望.
(参考数据:若X~N( ,σ2),有P( ﹣σ<X≤ +σ)=0.68ξ26,P(ξ ﹣2σ<X≤ +2σ)=0.9544,P
( ﹣3σ<X≤ +3σ)=0μ.9974.) μ μ μ μ
【μ分析】(Ⅰ)μ 由于随机变量X服从正态分布N(500,1002),由正态分布的对称性,可知P(x≤500)
= ,由此能求出p 的值.
0
(Ⅱ)英语和数学双科都超过600分的有5人,仅单科超过600分的有8人, 的所有取值有
0,1,2,3,分别求出相应的概率,由此能求出 的分布列和E( ).
ξ
【解答】解:(Ⅰ)由于随机变量X服从正态分布N(500,1002),
ξ ξ
∴ =500,σ=100,
P(X>600)=1﹣P(X≤600),
μ
由正态分布的对称性,可知P(x≤500)= ,
则P(400<X≤600)=0.6826,
则p=P(X>600)=1﹣P(X≤600)
0
=1﹣[P(X≤500)+ P(400<X≤600)]
=1﹣( )
=1﹣(0.5+0.3413)
=0.1587.
(Ⅱ)英语和数学双科都超过600分的有5人,仅单科超过600分的有8人,
的所有取值有0,1,2,3,
P( =0)= = ,
ξ
P( =1)= = ,
ξ
P( =2)= = ,
ξ
P( =3)= = ,
ξ
∴ 的分布列为:
ξ
0 1 2 3
ξ
ξ P
E( )= = .
【知识点】正态分布曲线的特点及曲线所表示的意义、离散型随机变量的期望与方差、离散型随机变量及
ξ
其分布列
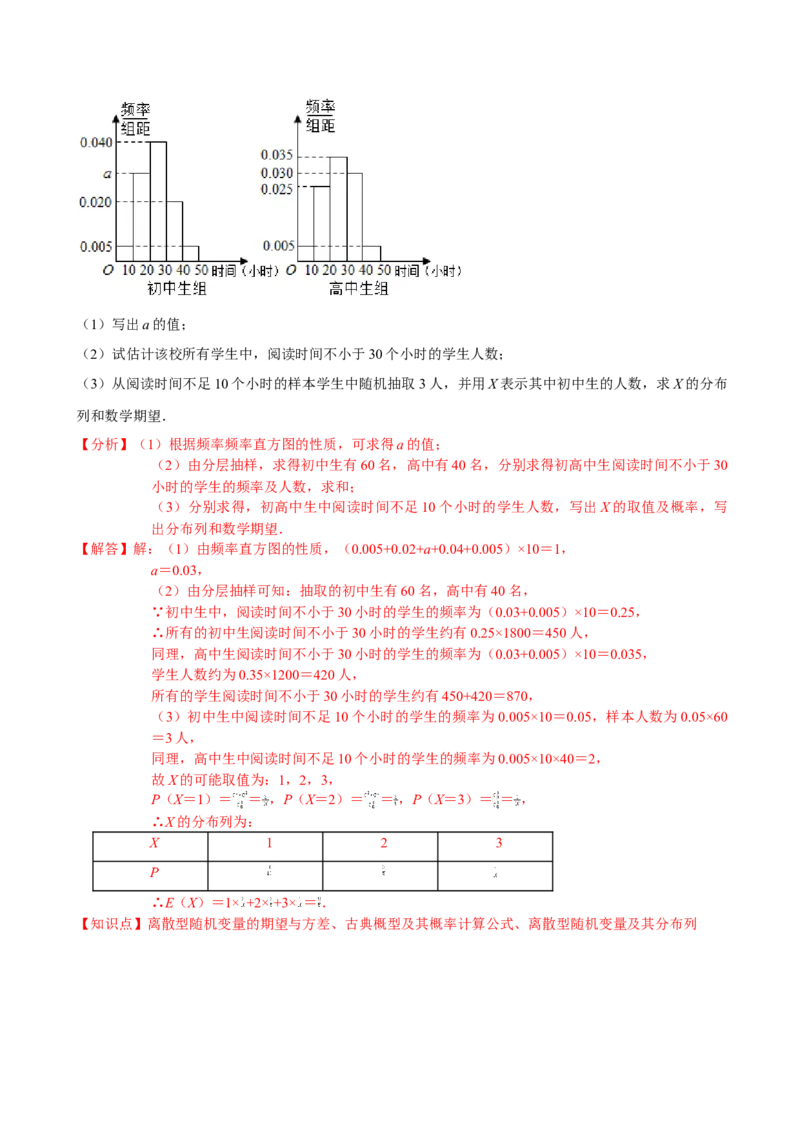
22.某中学有初中学生1800人,高中学生1200人,为了解学生本学期课外阅读时间,现采用分成抽样的方
法,从中抽取了100名学生,先统计了他们课外阅读时间,然后按“初中学生”和“高中学生”分为
两组,再将每组学生的阅读时间(单位:小时)分为 5组:[0,10),[10,20),[20,30),[30,
40),[40,50],并分别加以统计,得到如图所示的频率分布直方图.(1)写出a的值;
(2)试估计该校所有学生中,阅读时间不小于30个小时的学生人数;
(3)从阅读时间不足10个小时的样本学生中随机抽取3人,并用X表示其中初中生的人数,求X的分布
列和数学期望.
【分析】(1)根据频率频率直方图的性质,可求得a的值;
(2)由分层抽样,求得初中生有60名,高中有40名,分别求得初高中生阅读时间不小于30
小时的学生的频率及人数,求和;
(3)分别求得,初高中生中阅读时间不足10个小时的学生人数,写出X的取值及概率,写
出分布列和数学期望.
【解答】解:(1)由频率直方图的性质,(0.005+0.02+a+0.04+0.005)×10=1,
a=0.03,
(2)由分层抽样可知:抽取的初中生有60名,高中有40名,
∵初中生中,阅读时间不小于30小时的学生的频率为(0.03+0.005)×10=0.25,
∴所有的初中生阅读时间不小于30小时的学生约有0.25×1800=450人,
同理,高中生阅读时间不小于30小时的学生的频率为(0.03+0.005)×10=0.035,
学生人数约为0.35×1200=420人,
所有的学生阅读时间不小于30小时的学生约有450+420=870,
(3)初中生中阅读时间不足10个小时的学生的频率为0.005×10=0.05,样本人数为0.05×60
=3人,
同理,高中生中阅读时间不足10个小时的学生的频率为0.005×10×40=2,
故X的可能取值为:1,2,3,
P(X=1)= = ,P(X=2)= = ,P(X=3)= = ,
∴X的分布列为:
X 1 2 3
P
∴E(X)=1× +2× +3× = .
【知识点】离散型随机变量的期望与方差、古典概型及其概率计算公式、离散型随机变量及其分布列