文档内容
保密★启⽤前
年上学期⾼⼀年级期末考试(数学)试题卷
2025
班级:___________姓名:___________考号:___________
⼀、选择题:本⼤题共8⼩题,每⼩题5分,共40分.在每⼩题给出的四个选项中,只有⼀项
是符合题⽬要求的,请把答案填涂在答题卡相应位置上.
1.为了了解邵东市中⼩学⽣的视⼒情况,拟从邵东市的中⼩学⽣中抽取部分学⽣进⾏调查,事先已经了解
到邵东市⼩学、初中、⾼中三个学段学⽣的视⼒情况有较⼤差异,⽽男、⼥⽣视⼒情况差异不⼤.则下列抽样
⽅法最合理的是( )
A.简单随机抽样 B.按性别分层抽样 C.按学段分层抽样 D.按性别或学段分层抽样都⾏
2.复数 的虚部为( )
A.1 B. C. D.
3.设 是⼀个平⾯, 、 是两条直线,则正确的命题为( )
A.如果 , ,那么 B.如果 , ,那么
C.如果 , ,那么 D.如果 , ,那么
4.已知在 中, ,则 的形状是( )
A.等腰三⻆形 B.等边三⻆形 C.钝⻆三⻆形 D.直⻆三⻆形
5.已知平⾯向量 ,若 与 垂直,则 ( )
A. B. C. D.14
6.⼩明参加⼀场射箭⽐赛,需要连续射击三个靶⼦,每次射箭结果互不影响,已知他射中这三个靶⼦的概
率分别为x,x, ,若他恰好射中两个靶⼦的概率是 ,那么他三个靶⼦都没射中的概率是( )
A. B. C. D.
7.在 中,点 在线段 上,且满⾜ ,点 为线段 上任意⼀点(除端点外),
若实数 , 满⾜ ,则 的最⼩值为( )
A. B. C. D.9
8.在三棱锥 中, , , ,则该三棱锥的外接球
的表⾯积为( )
学科⽹(北京)股份有限公司A. B. C. D.
⼆、选择题:本⼤题共3⼩题,每⼩题6分,共18分.在每⼩题给出的四个选项中,有多项符合题⽬要求,
请把答案填涂在答题卡相应位置上.全部选对得6分,部分选对得部分分,不选或有错选的得0分.
9.在⼀次随机试验中,彼此互斥的事件A,B,C,D发⽣的概率分别是0.1,0.2,0.3,0.4,则下列说法错
误的是( )
A. 与C是互斥事件,也是对⽴事件 B. 与D是互斥事件,也是对⽴事件
C. 与 是互斥事件,但不是对⽴事件 D.A与 是互斥事件,也是对⽴事件
10.在 中,内⻆ 所对的边分别为 ,则下列说法正确的是( )
A.若 ,则 是钝⻆三⻆形
B.若 是锐⻆三⻆形,则
C.若 , , ,则满⾜这组条件的三⻆形有两个
D.若 ,则
11.正⽅体 的棱⻓为2, 是侧⾯ 上的⼀个动点(含边界);点 在棱
上, ;则下列结论正确的有( )
A.沿正⽅体的表⾯从点 到点 的最短距离为
B.三棱锥 的外接球表⾯积为
C.若 ,则点 的运动轨迹⻓度为
D.平⾯ 被正⽅体 截得截⾯⾯积为
三、填空题:本⼤题共3⼩题,每⼩题5分,共15分.请把答案填写在答题卡相应位置上.
12.在⼀次数学测验中,某⼩组的7位同学的成绩分别为:109,116,122,126,131,134,140,则这7
位同学成绩的上四分位数与下四分位数的差为__________.
13.已知 是边⻓为2的等边三⻆形,点 是 内⼀点,且 ,若 ,
则 的最⼩值为__________.
14.在三棱锥 中, ,点P在平⾯ABC上的投影O是 的垂⼼, 平⾯PBC,
若 ,则三棱锥 的体积的最⼤值为__________.
四、解答题:本⼤题共5⼩题,共77分.请在答题卡指定区域内作答,解答时应写出必要的⽂
字说明,证明过程或演算步骤.
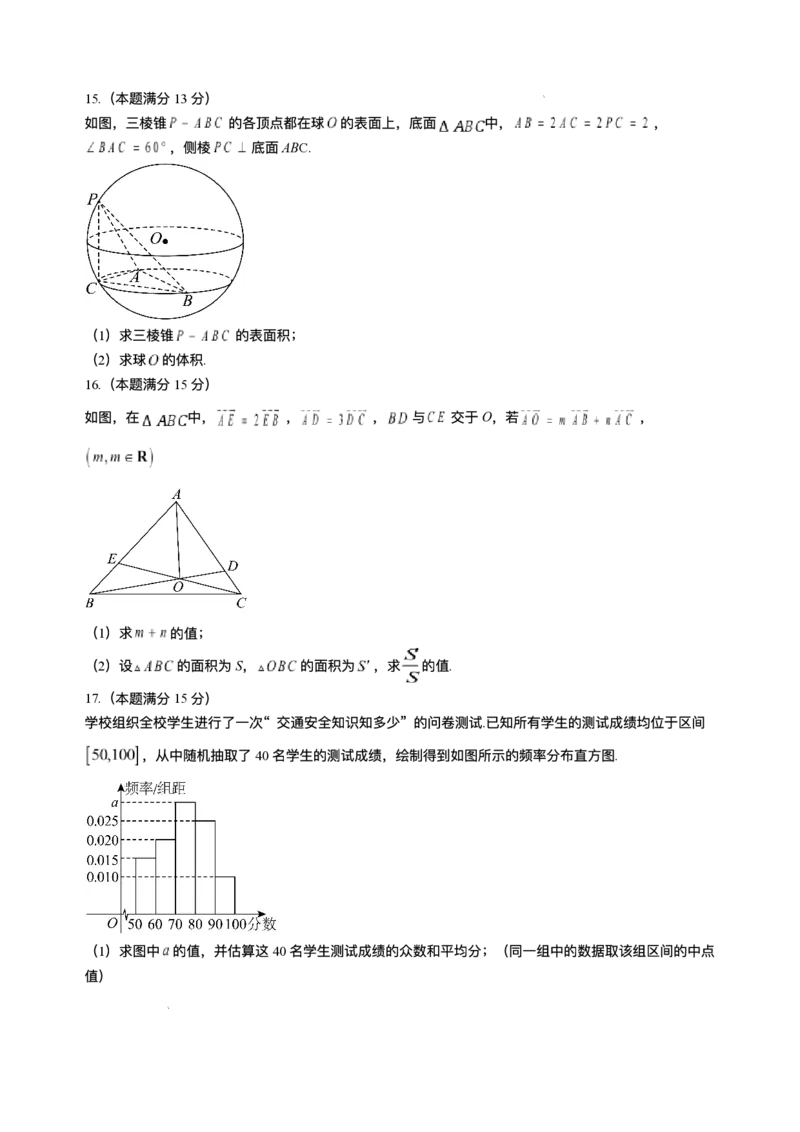
学科⽹(北京)股份有限公司15.(本题满分13分)
如图,三棱锥 的各顶点都在球 的表⾯上,底⾯ 中, ,
,侧棱 底⾯ABC.
(1)求三棱锥 的表⾯积;
(2)求球 的体积.
16.(本题满分15分)
如图,在 中, , , 与 交于O,若 ,
(1)求 的值;
(2)设 的⾯积为S, 的⾯积为 ,求 的值.
17.(本题满分15分)
学校组织全校学⽣进⾏了⼀次“ 交通安全知识知多少” 的问卷测试.已知所有学⽣的测试成绩均位于区间
,从中随机抽取了40名学⽣的测试成绩,绘制得到如图所示的频率分布直⽅图.
(1)求图中 的值,并估算这40名学⽣测试成绩的众数和平均分;(同⼀组中的数据取该组区间的中点
值)
学科⽹(北京)股份有限公司(2)我校2025年全⼒推进校园信息化建设.为了更好的帮助同学们了解学校的信息化建设情况,学校政教
处利⽤⽐例分配的分层随机抽样⽅法,从 和 的学⽣中抽取7⼈组成“ 信息化建设” 宣讲
团.
①求应从 和 学⽣中分别抽取的学⽣⼈数;
②从选定的7⼈中随机抽取2⼈对⾼⼀同学进⾏宣讲,设事件 “ ⾄少有1⼈测试成绩位于区间
” ,求事件 的概率.
18.(本题满分17分)
在 中,内⻆A,B,C对边分别为a,b,c,已知 .
(1)求⻆A的值;
(2)若 .
①求a的值;
②求 ⾯积的最⼤值.
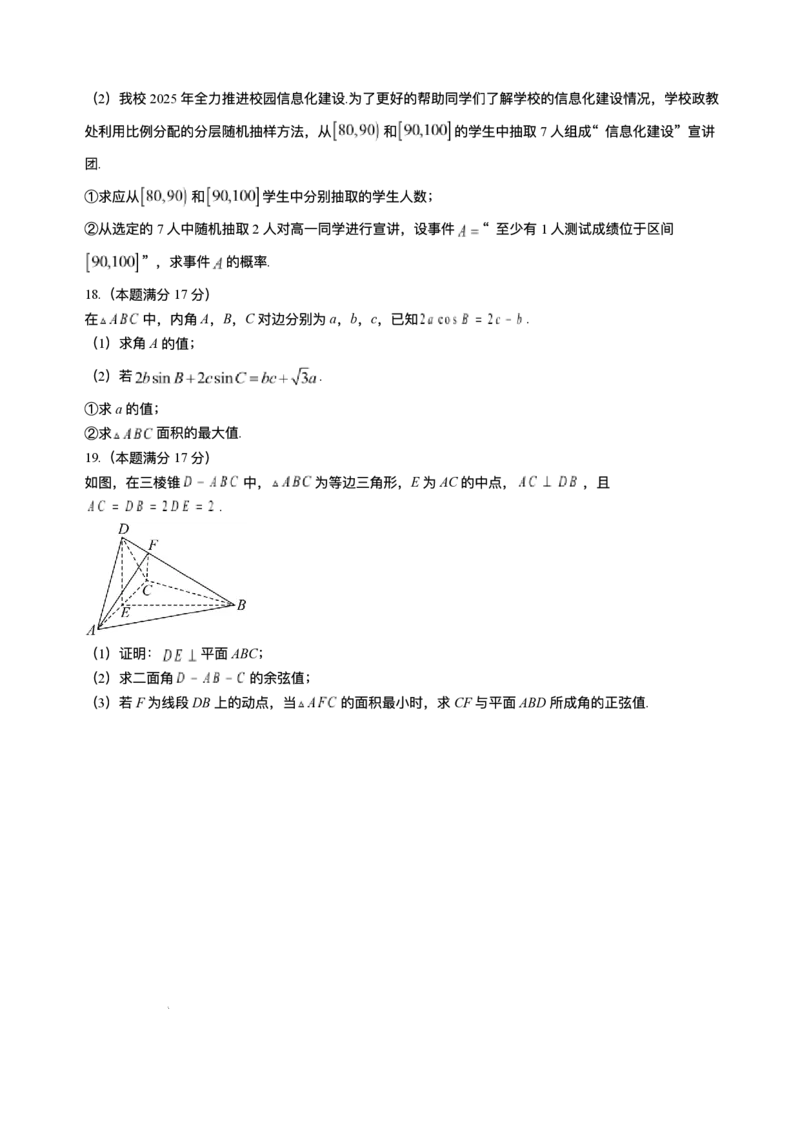
19.(本题满分17分)
如图,在三棱锥 中, 为等边三⻆形,E为AC的中点, ,且
.
(1)证明: 平⾯ABC;
(2)求⼆⾯⻆ 的余弦值;
(3)若F为线段DB上的动点,当 的⾯积最⼩时,求CF与平⾯ABD所成⻆的正弦值.
学科⽹(北京)股份有限公司年上学期⾼⼀年级期末考试(数学)
2025
参考答案
⼀、单选题
1 2 3 4 5 6 7 8
C A D B B C D D
⼆、多选题
9 10 11
ABC AB BC
D D
三、填空题
12 13 14
18
四、解答题
15.(1)在底⾯ 中,由 ,可得 ,
⼜ ,由余弦定理可得, ,
所以 ,即 ,
故 .
⼜ ,侧棱 底⾯ ,
所以 ,
学科⽹(北京)股份有限公司⼜ 且 ,
则 为等腰三⻆形,设 边上的⾼为 ,
则 ,
所以三棱锥 的表⾯积为 .
(2)设球 的半径为 .因为 ,
所以三棱锥 外接球与以 为棱的⻓⽅体的外接球是同⼀个球,
即球 的直径恰好是以 为棱的⻓⽅体的体对⻆线,
故 ,故球 的半径 ,
所以球 的体积为.
16.(1) ,
因为 三点共线,所以 ,
⼜因为 ,所以 ,则 ,
同理,因为 三点共线,所以 ,
⼜因为 ,所以 ,则 ,
根据平⾯向量基本定理,可得 ,解得 ,
所以
(2)延⻓ 与 交于点 ,因为 三点共线,
所以
,
学科⽹(北京)股份有限公司⼜因为 ,且 ,所以 ,
即 ,
所以 ,解得 ,所以 ,则
所以 .
17.(1)由频率分布直⽅图可得 ,
解得 ;
由频率分布图可知众数约为75;
估算这40名学⽣测试成绩的平均数为
(2)①由图可得 和 这两组的频率之⽐为 ,
故应从 学⽣中抽取的学⽣⼈数为 (⼈),
应从 学⽣中抽取的学⽣⼈数为 (⼈);
②设从 中抽取的5⼈为 ,从 学⽣中抽取的2⼈为1,2,
则这个试验的样本空间为 ,
共有21个基本事件;
事件 “ ⾄少有1⼈测试成绩位于区间 ” ,事件 的个数有11个,即
,
故 .
18.(1) ,
,
化简可得: ,
,
,
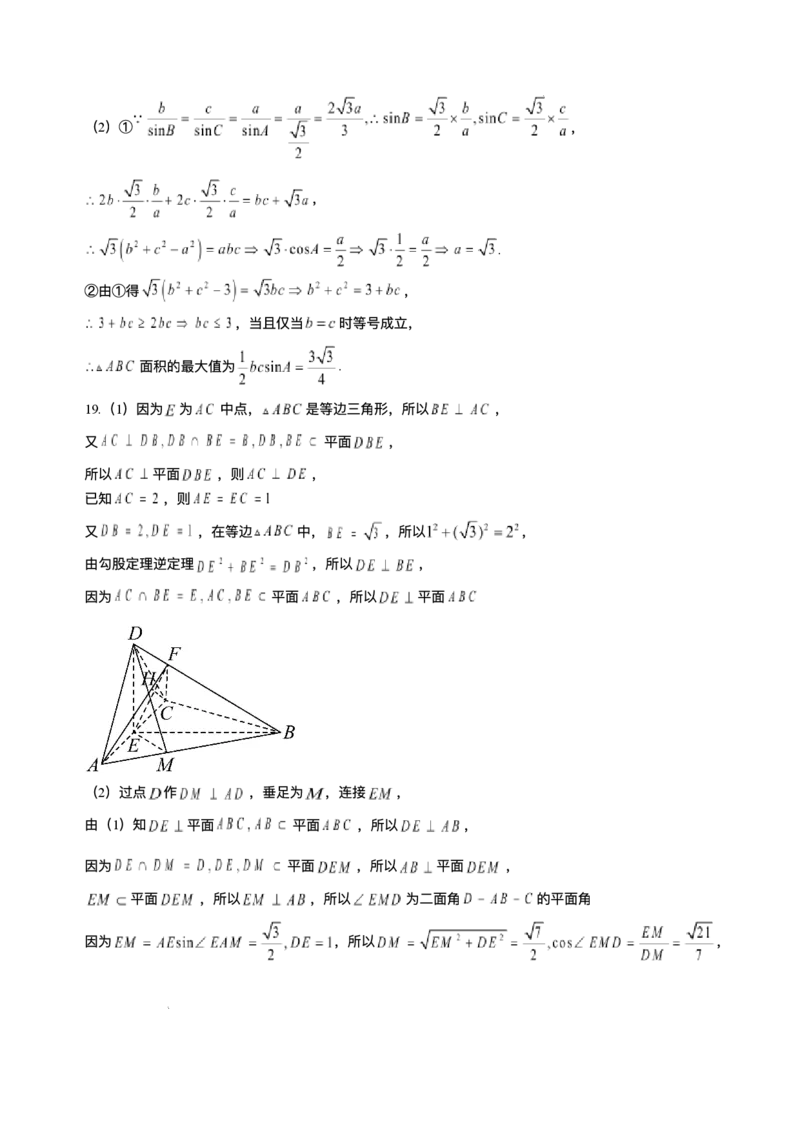
学科⽹(北京)股份有限公司(2)① ,
,
.
②由①得 ,
,当且仅当 时等号成⽴,
⾯积的最⼤值为 .
19.(1)因为 为 中点, 是等边三⻆形,所以 ,
⼜ 平⾯ ,
所以 平⾯ ,则 ,
已知 ,则
⼜ ,在等边 中, ,所以 ,
由勾股定理逆定理 ,所以 ,
因为 平⾯ ,所以 平⾯
(2)过点 作 ,垂⾜为 ,连接 ,
由(1)知 平⾯ 平⾯ ,所以 ,
因为 平⾯ ,所以 平⾯ ,
平⾯ ,所以 ,所以 为⼆⾯⻆ 的平⾯⻆
因为 ,所以 ,
学科⽹(北京)股份有限公司所以⼆⾯⻆ 的余弦值为
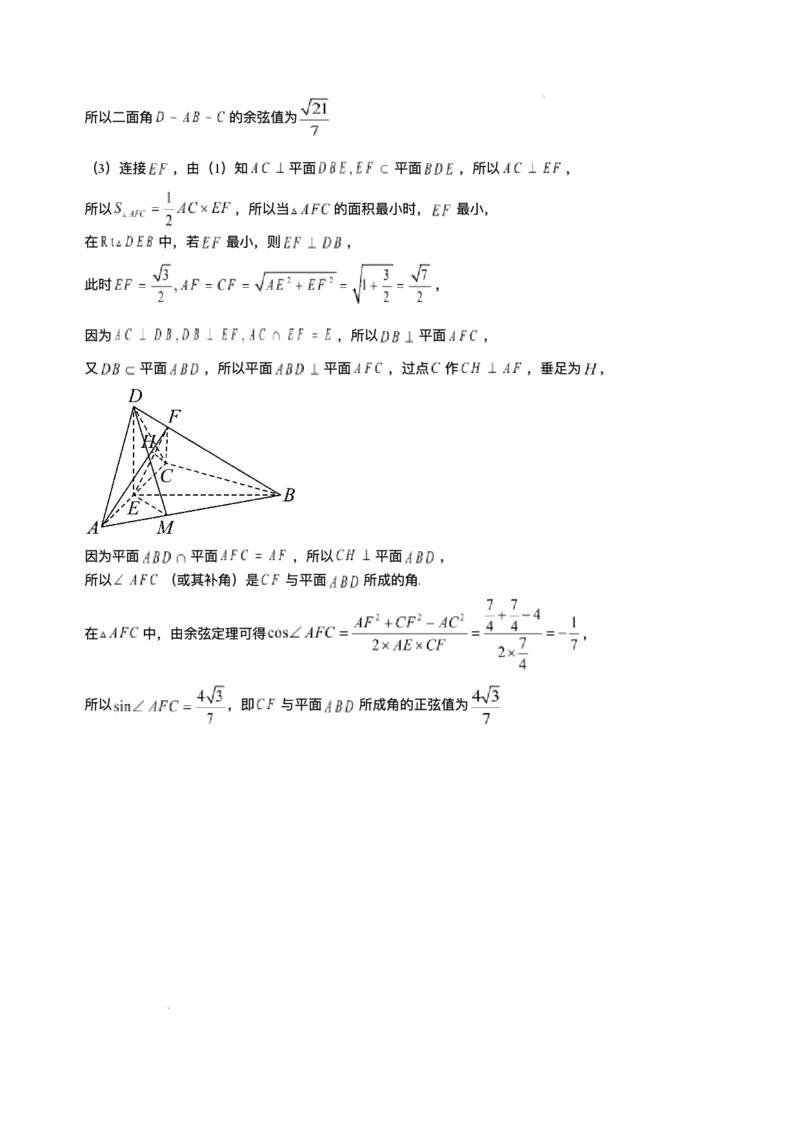
(3)连接 ,由(1)知 平⾯ 平⾯ ,所以 ,
所以 ,所以当 的⾯积最⼩时, 最⼩,
在 中,若 最⼩,则 ,
此时 ,
因为 ,所以 平⾯ ,
⼜ 平⾯ ,所以平⾯ 平⾯ ,过点 作 ,垂⾜为 ,
因为平⾯ 平⾯ ,所以 平⾯ ,
所以 (或其补⻆)是 与平⾯ 所成的⻆.
在 中,由余弦定理可得 ,
所以 ,即 与平⾯ 所成⻆的正弦值为
学科⽹(北京)股份有限公司