2000年天津高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_天津

2000 年天津高考文科数学真题及答案
一、选择题（共12小题，每小题4分，满分48分）
1．（4分）设集合A{x|xZ 且10„ x„ 1}，B{x|xZ ，且|x|„ 5}，则A B中的元

素个数是( )
A．11 B．10 C．16 D．15
2．（4分）设a、b  、c是任意的非零平面向量，且相互不共线，则( )
①(a b  )c(c a)b  0；
 
②|a||b  ||ab  |；
③(b  c)a(a c)b  不与c垂直；
 
④(3a2b  ) (3a2b  )9|a|2 4|b  |2．

其中的真命题是( )
A．②④ B．③④ C．②③ D．①②
3．（4分）一个长方体共一顶点的三个面的面积分别是 2， 3， 6 ，这个长方体对角线
的长是( )
A．2 3 B．3 2 C．6 D． 6
4．（4分）已知sinsin，那么下列命题成立的是( )
A．若、是第一象限角，则coscos
B．若、是第二象限角，则tantan
C．若、是第三象限角，则coscos
D．若、是第四象限角，则tantan
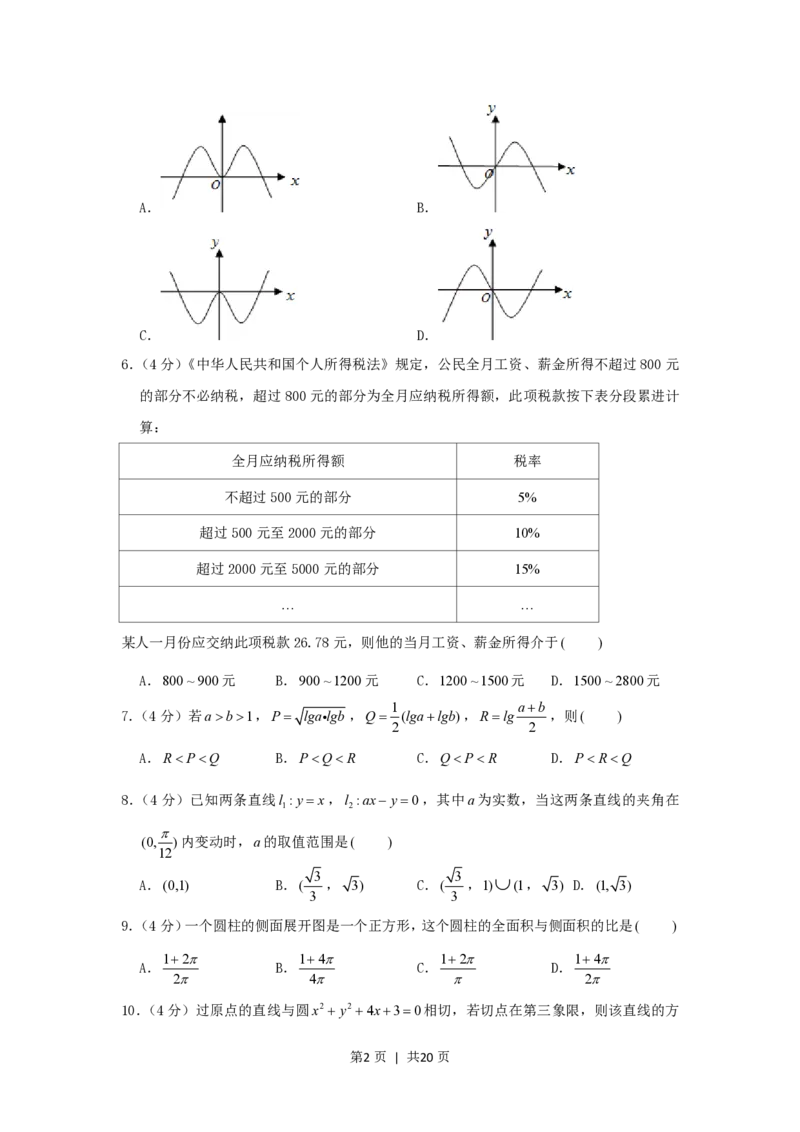
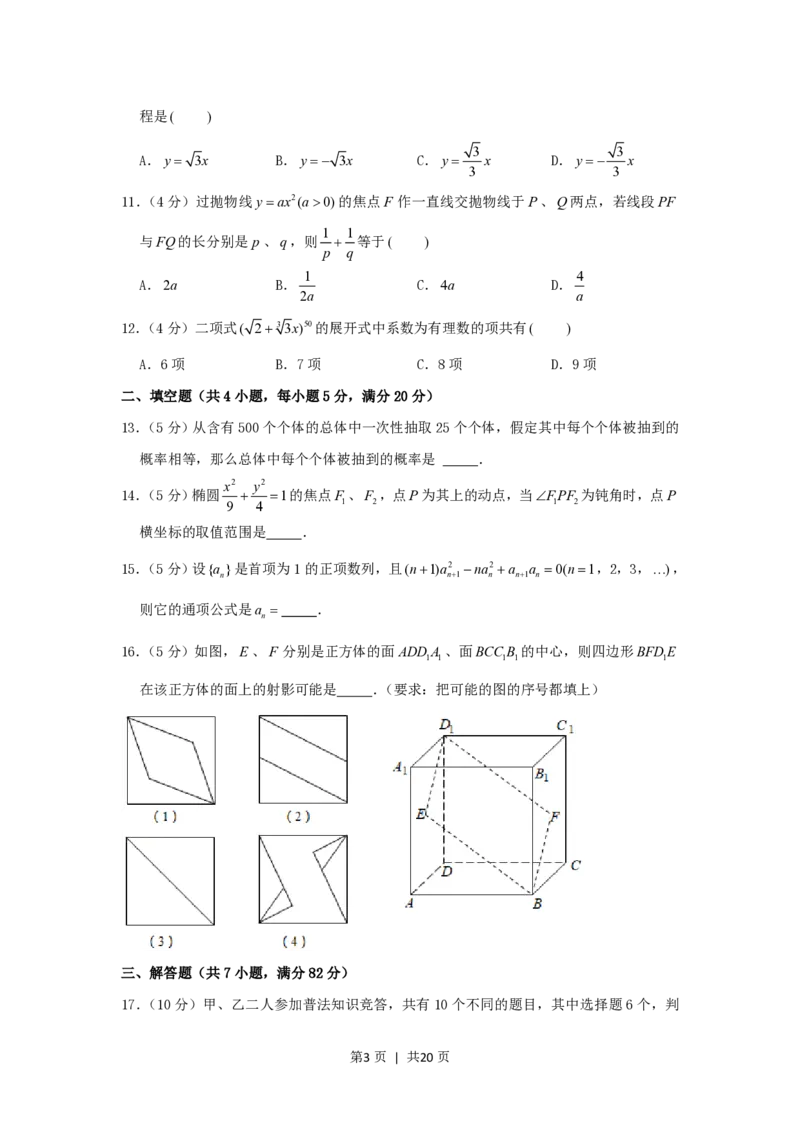
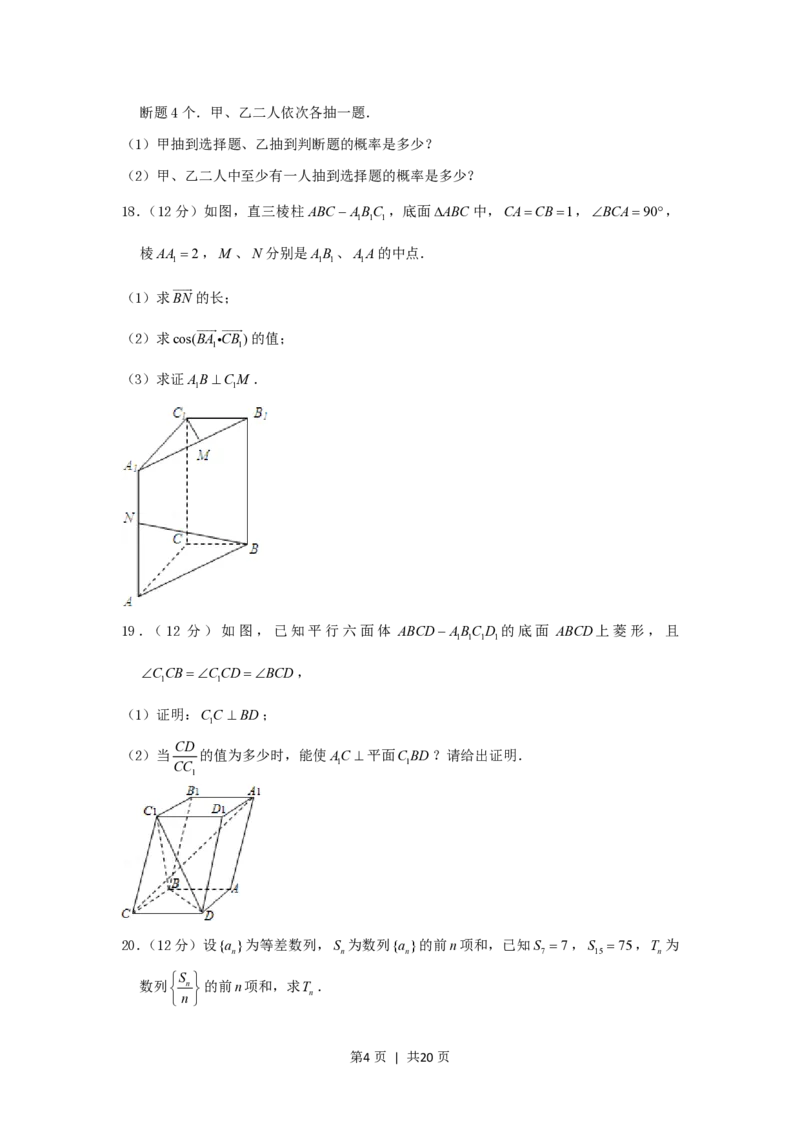
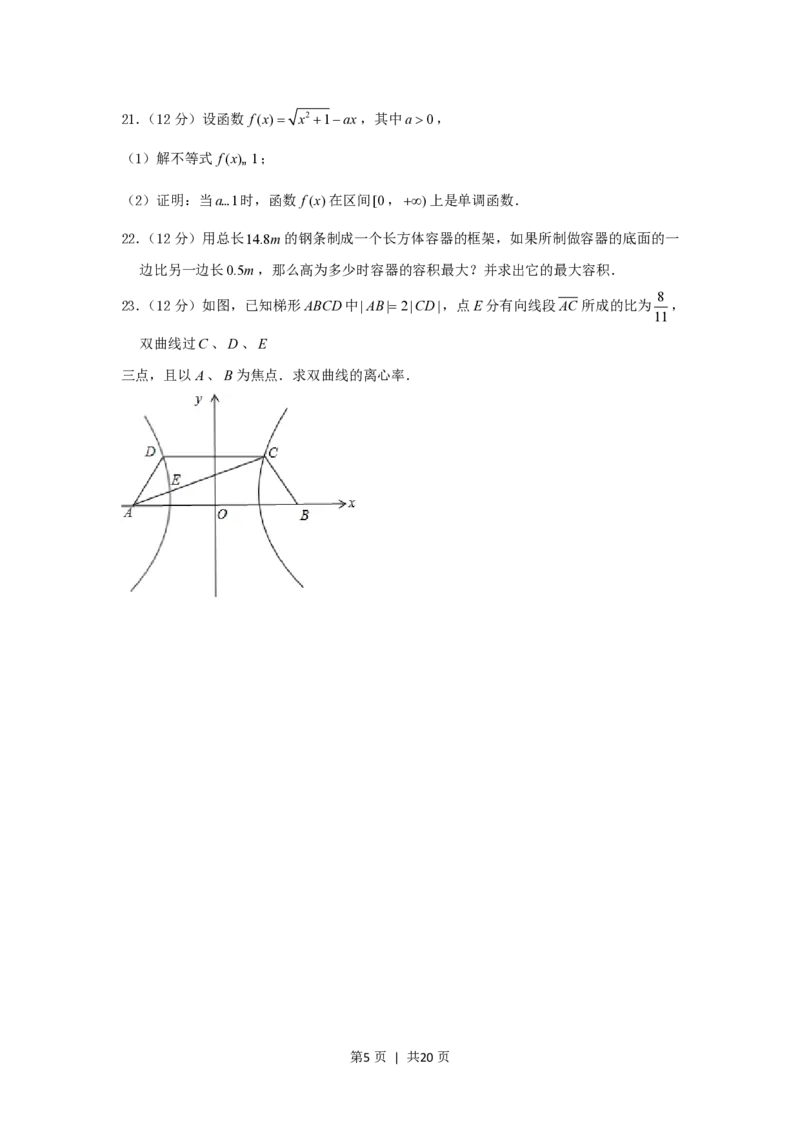
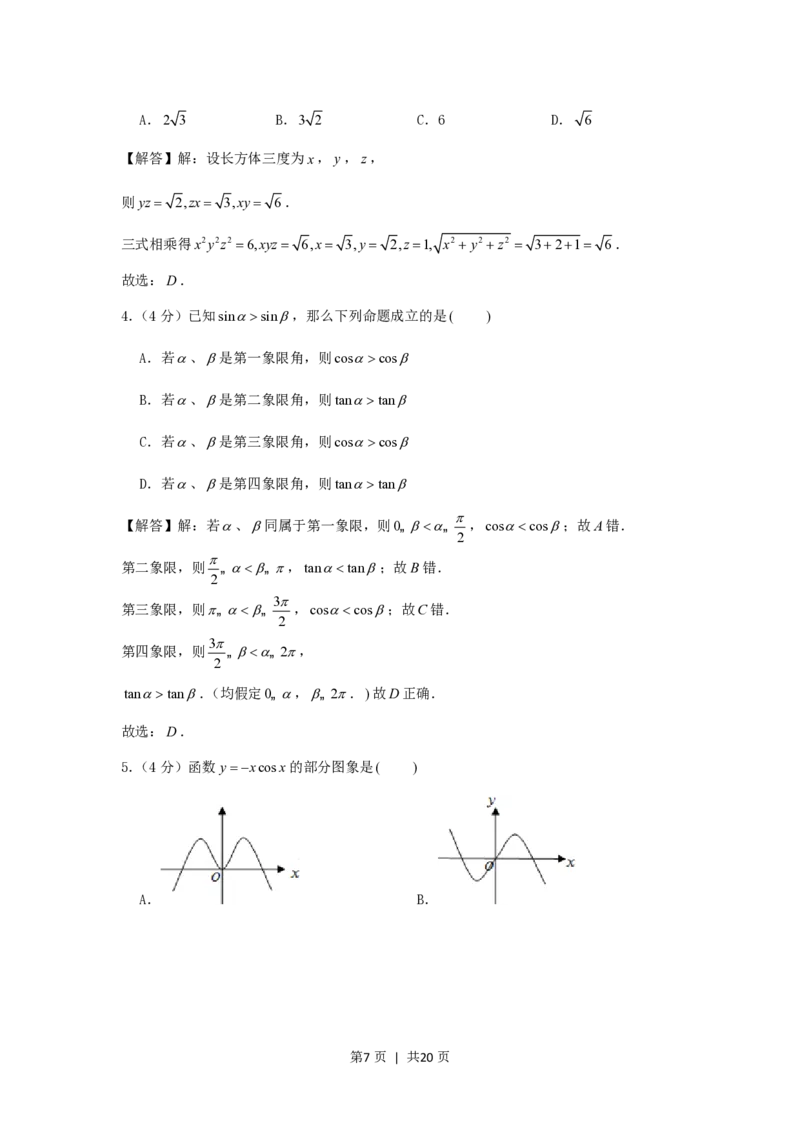
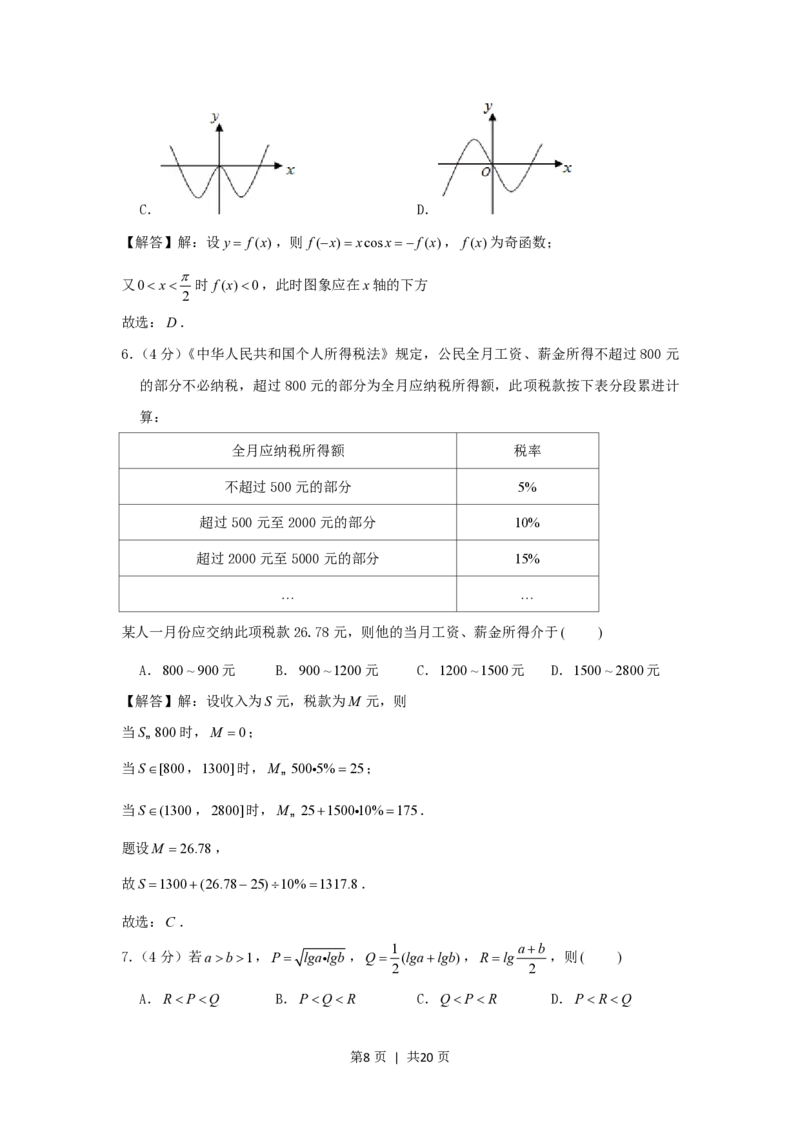
5．（4分）函数yxcosx的部分图象是( )
第1页 | 共20页A． B．
C． D．
6．（4分）《中华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过800元
的部分不必纳税，超过800元的部分为全月应纳税所得额，此项税款按下表分段累进计
算：
全月应纳税所得额 税率
不超过500元的部分 5%
超过500元至2000元的部分 10%
超过2000元至5000元的部分 15%
 
某人一月份应交纳此项税款26.78元，则他的当月工资、薪金所得介于( )
A．800~900元 B．900~1200元 C．1200~1500元 D．1500~2800元
1 ab
7．（4分）若ab1，P lga lgb ，Q (lgalgb)，Rlg ，则( )

2 2
A．RPQ B．PQR C．QPR D．PRQ
8．（4分）已知两条直线l :yx，l :ax y0，其中a为实数，当这两条直线的夹角在
1 2

(0, )内变动时，a的取值范围是( )
12
3 3 
A．(0,1) B．( ， 3) C．( ，1) (1， 3) D．(1, 3)
3 3
9．（4分）一个圆柱的侧面展开图是一个正方形，这个圆柱的全面积与侧面积的比是( )
12 14 12 14
A． B． C． D．
2 4  2
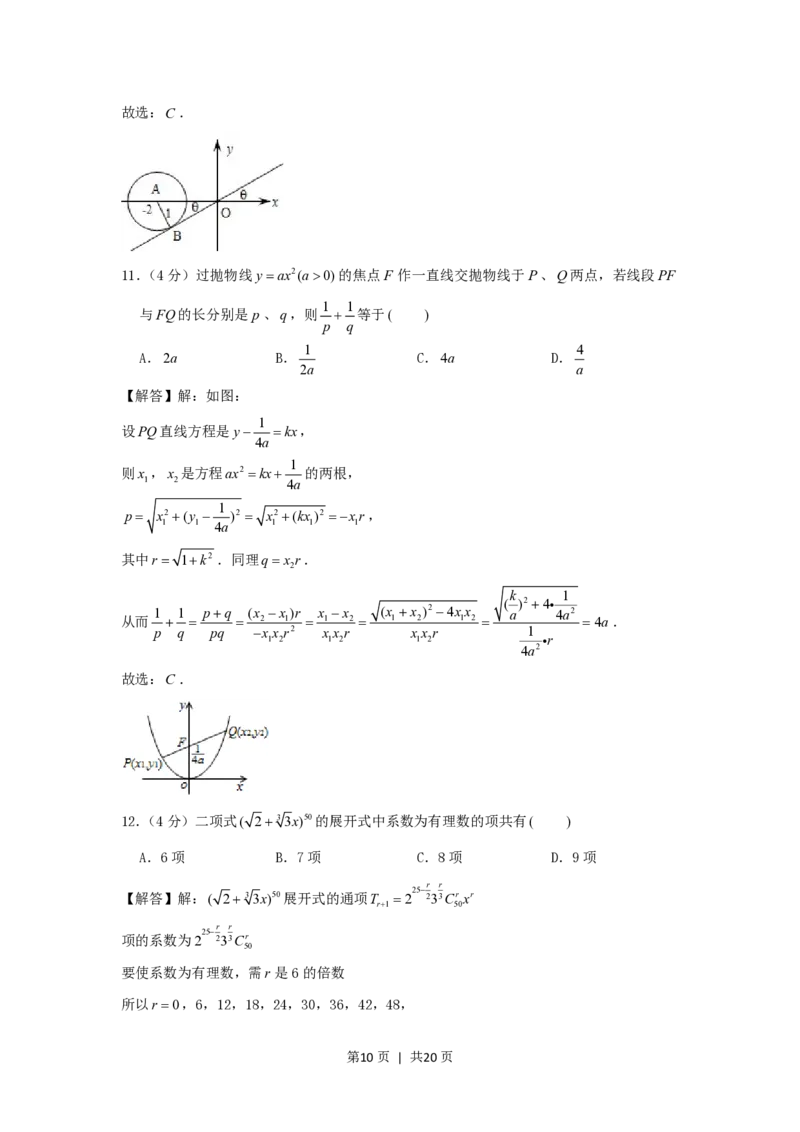
10．（4分）过原点的直线与圆x2  y2 4x30相切，若切点在第三象限，则该直线的方
第2页 | 共20页程是( )
3 3
A．y 3x B．y 3x C．y x D．y x
3 3
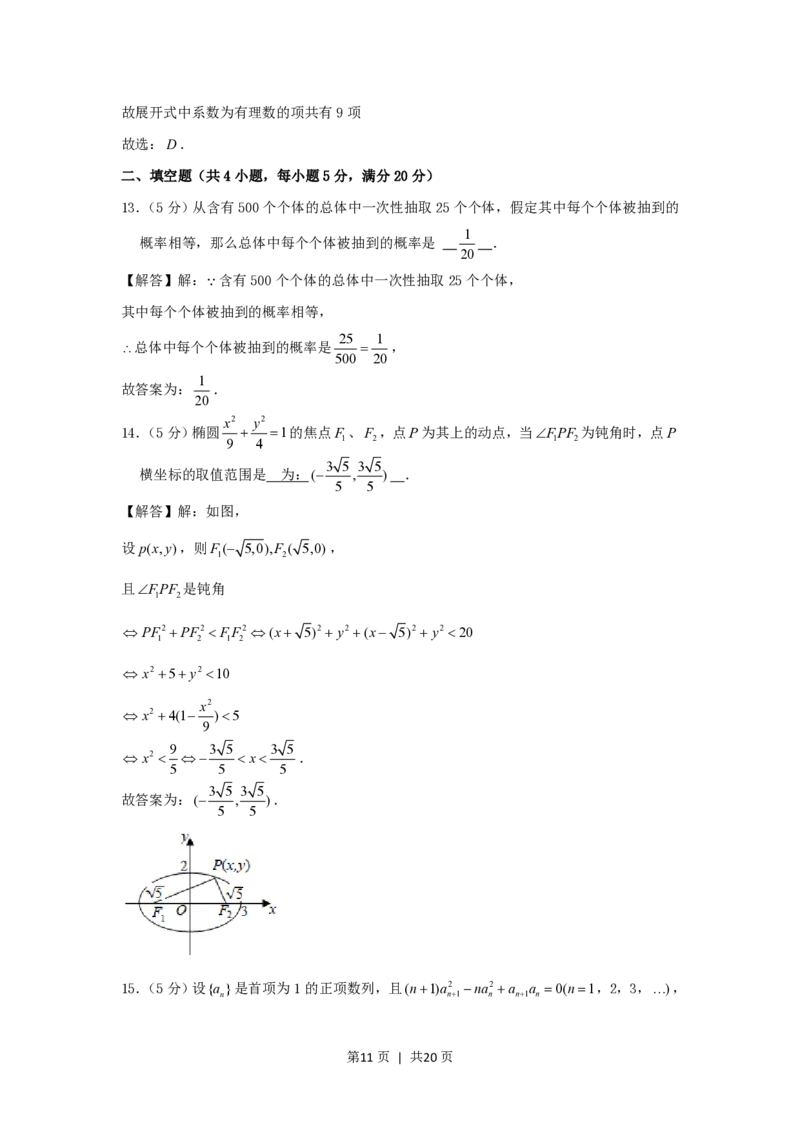
11．（4分）过抛物线yax2(a0)的焦点F 作一直线交抛物线于P、Q两点，若线段PF
1 1
与FQ的长分别是 p、q，则  等于( )
p q
1 4
A．2a B． C．4a D．
2a a
12．（4分）二项式( 2 33x)50的展开式中系数为有理数的项共有( )
A．6项 B．7项 C．8项 D．9项
二、填空题（共4小题，每小题5分，满分20分）
13．（5分）从含有500个个体的总体中一次性抽取25个个体，假定其中每个个体被抽到的
概率相等，那么总体中每个个体被抽到的概率是 ．
x2 y2
14．（5分）椭圆  1的焦点F 、F ，点P为其上的动点，当FPF 为钝角时，点P
9 4 1 2 1 2
横坐标的取值范围是 ．
15．（5分）设{a }是首项为1的正项数列，且(n1)a2 na2 a a 0(n1，2，3，)，
n n1 n n1 n
则它的通项公式是a  ．
n
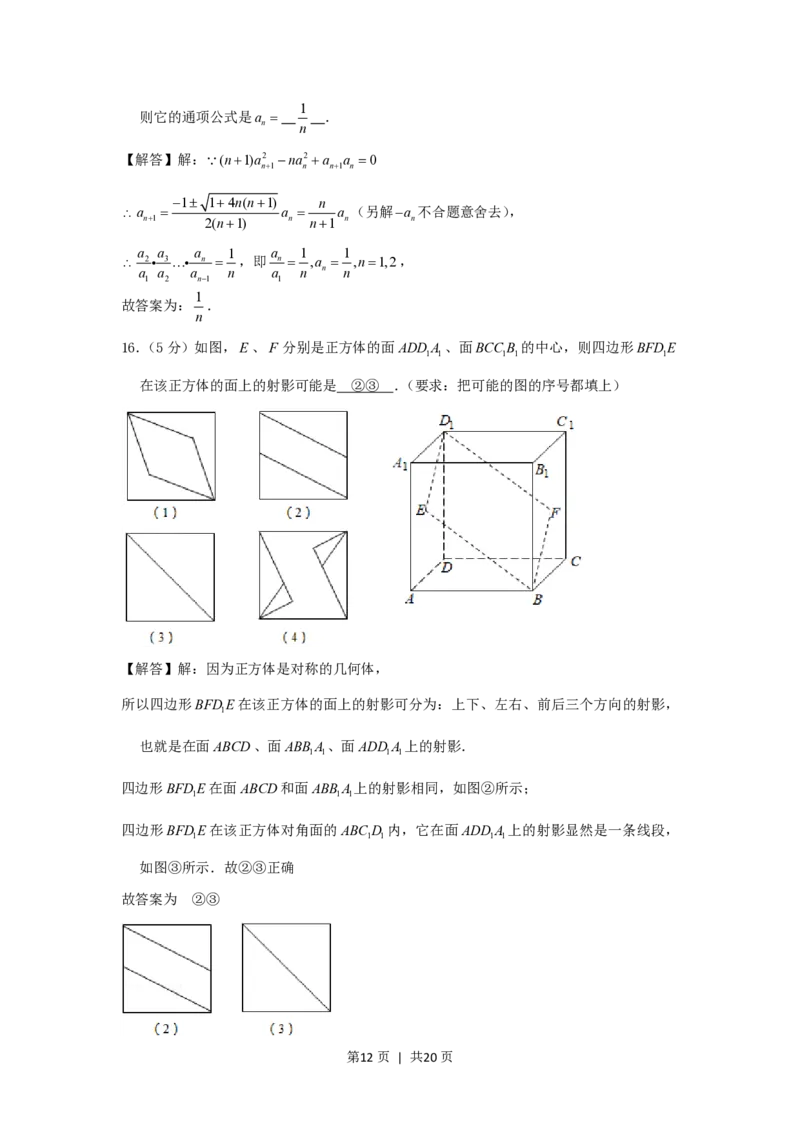
16．（5分）如图，E、F 分别是正方体的面ADDA 、面BCCB 的中心，则四边形BFDE
1 1 1 1 1
在该正方体的面上的射影可能是 ．（要求：把可能的图的序号都填上）
三、解答题（共7小题，满分82分）
17．（10分）甲、乙二人参加普法知识竞答，共有10个不同的题目，其中选择题6个，判
第3页 | 共20页断题4个．甲、乙二人依次各抽一题．
（1）甲抽到选择题、乙抽到判断题的概率是多少？
（2）甲、乙二人中至少有一人抽到选择题的概率是多少？
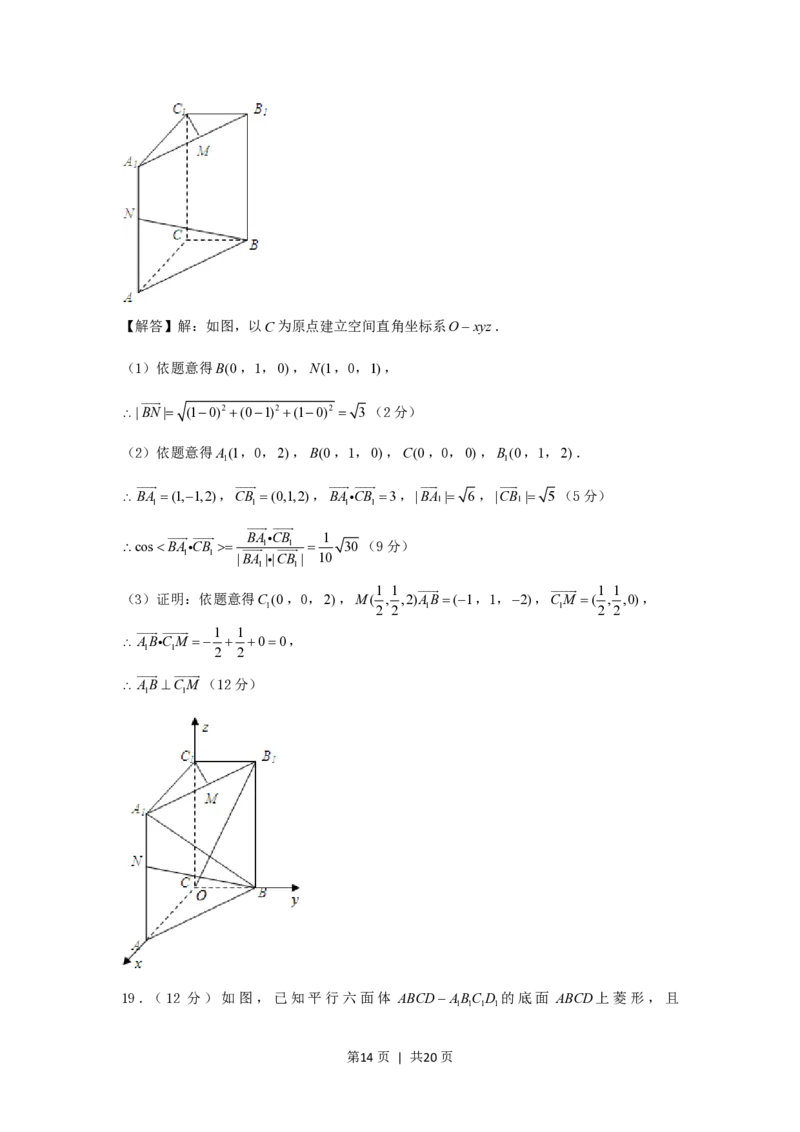
18．（12分）如图，直三棱柱ABCABC ，底面ABC 中，CACB1，BCA90，
1 1 1
棱AA 2，M 、N分别是AB 、AA的中点．
1 1 1 1

（1）求BN 的长；
 
（2）求cos(BA CB)的值；
1 1
（3）求证ABCM ．
1 1
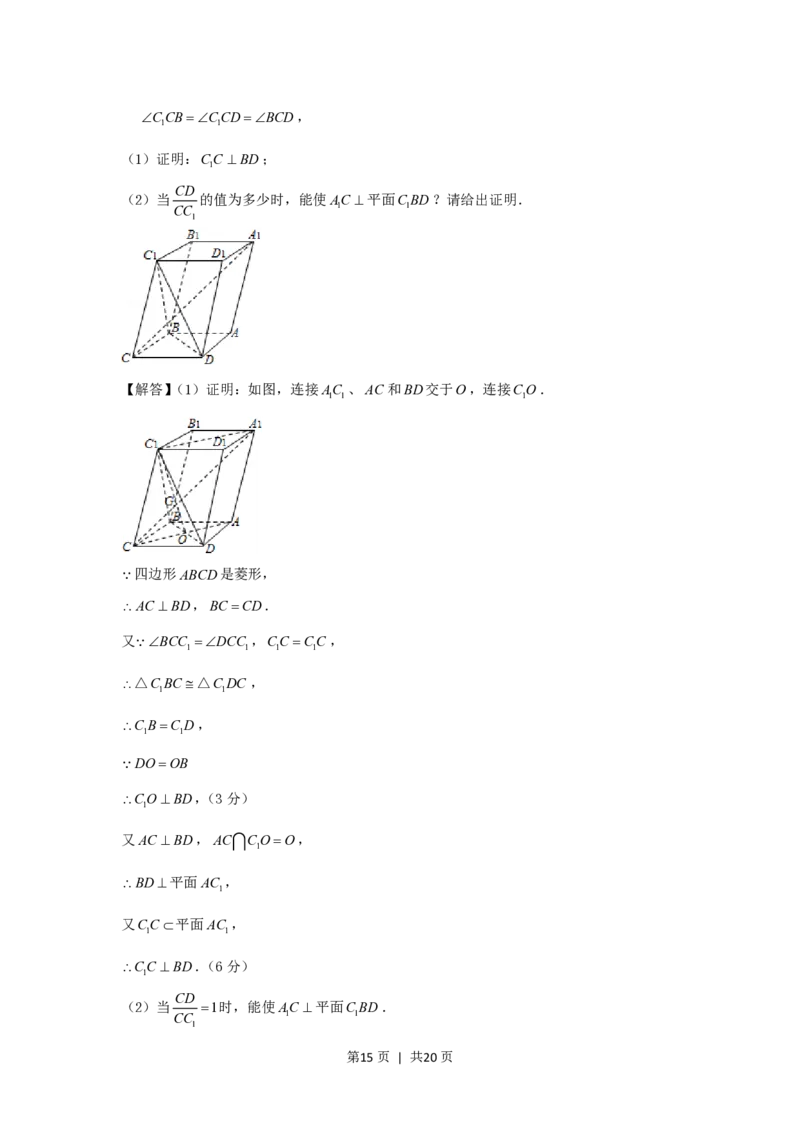
19．（12 分）如图，已知平行六面体 ABCDABCD 的底面 ABCD上菱形，且
1 1 1 1
CCBCCDBCD，
1 1
（1）证明：CC BD；
1
CD
（2）当 的值为多少时，能使AC 平面CBD？请给出证明．
CC 1 1
1
20．（12分）设{a }为等差数列，S 为数列{a }的前n项和，已知S 7，S 75，T 为
n n n 7 15 n
S 
数列 n的前n项和，求T ．
 n  n
第4页 | 共20页21．（12分）设函数 f(x) x2 1ax，其中a0，
（1）解不等式 f(x)„1；
（2）证明：当a…1时，函数 f(x)在区间[0，)上是单调函数．
22．（12分）用总长14.8m的钢条制成一个长方体容器的框架，如果所制做容器的底面的一
边比另一边长0.5m，那么高为多少时容器的容积最大？并求出它的最大容积．
8
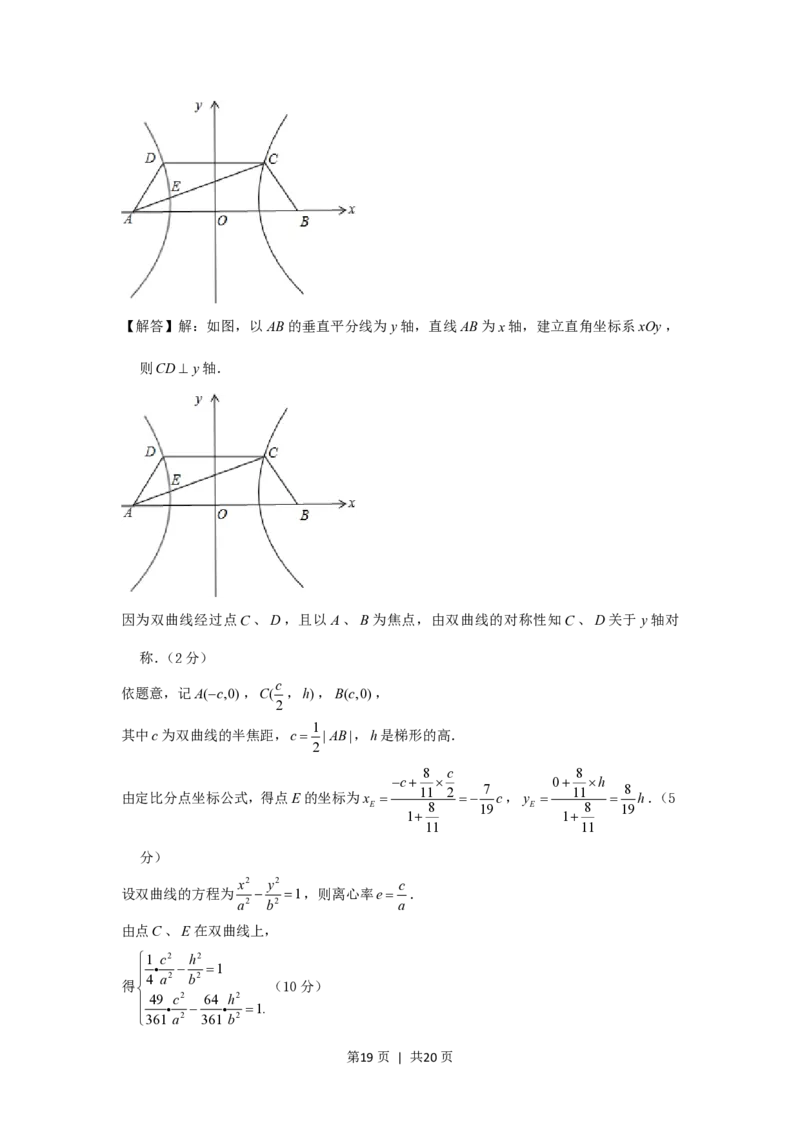
23．（12分）如图，已知梯形ABCD中|AB|2|CD|，点E分有向线段AC所成的比为 ，
11
双曲线过C、D、E
三点，且以A、B为焦点．求双曲线的离心率．
第5页 | 共20页2000年天津市高考数学试卷（文）
参考答案与试题解析
一、选择题（共12小题，每小题4分，满分48分）
1．（4分）设集合A{x|xZ 且10„ x„ 1}，B{x|xZ ，且|x|„ 5}，则A B中的元

素个数是( )
A．11 B．10 C．16 D．15
【解答】解：由集合A中的条件可得A中的元素有：10，9，8，，1共10个；
集合B中的不等式|x|„ 5解得5„ x„ 5且xZ ，所以B中的元素有：5，4，3，2，
1，0，1，2，3，4，5共11个
所以A B中的元素有：10，9，8，，1，0，1，2，3，4，5共16个

故选：C．
2．（4分）设a、b  、c是任意的非零平面向量，且相互不共线，则( )
①(a b  )c(c a)b  0；
 
②|a||b  ||ab  |；
③(b  c)a(a c)b  不与c垂直；
 
④(3a2b  ) (3a2b  )9|a|2 4|b  |2．

其中的真命题是( )
A．②④ B．③④ C．②③ D．①②
【解答】解：由于b  ,c是不共线的向量，因此(a b  )c不一定等于(c a)b  ，故①错误；
 
由于a,b  不共线，故a,b  ,(ab  )构成三角形，因此②正确；
由于[(b  c)a(c a)b  ]c(b  c)(a c)(c a)(b  c)0，故③中两向量垂直，故③错误；
      
根据向量数量积的运算可以得出④是正确的．故选A．
3．（4分）一个长方体共一顶点的三个面的面积分别是 2， 3， 6 ，这个长方体对角线
的长是( )
第6页 | 共20页A．2 3 B．3 2 C．6 D． 6
【解答】解：设长方体三度为x，y，z，
则yz 2,zx 3,xy 6．
三式相乘得x2y2z2 6,xyz 6,x 3,y 2,z1, x2  y2 z2  321 6．
故选：D．
4．（4分）已知sinsin，那么下列命题成立的是( )
A．若、是第一象限角，则coscos
B．若、是第二象限角，则tantan
C．若、是第三象限角，则coscos
D．若、是第四象限角，则tantan

【解答】解：若、同属于第一象限，则0„ „ ，coscos；故A错．
2

第二象限，则 „ „ ，tantan；故B错．
2
3
第三象限，则„ „ ，coscos；故C错．
2
3
第四象限，则 „ „ 2，
2
tantan．（均假定0„ ，„ 2．)故D正确．
故选：D．
5．（4分）函数yxcosx的部分图象是( )
A． B．
第7页 | 共20页C． D．
【解答】解：设y f(x)，则 f(x)xcosxf(x)， f(x)为奇函数；

又0x 时 f(x)0，此时图象应在x轴的下方
2
故选：D．
6．（4分）《中华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过800元
的部分不必纳税，超过800元的部分为全月应纳税所得额，此项税款按下表分段累进计
算：
全月应纳税所得额 税率
不超过500元的部分 5%
超过500元至2000元的部分 10%
超过2000元至5000元的部分 15%
 
某人一月份应交纳此项税款26.78元，则他的当月工资、薪金所得介于( )
A．800~900元 B．900~1200元 C．1200~1500元 D．1500~2800元
【解答】解：设收入为S元，税款为M 元，则
当S„ 800时，M 0；
当S[800，1300]时，M„ 500 5%25；

当S(1300，2800]时，M„ 25150010%175．

题设M 26.78，
故S 1300(26.7825)10%1317.8．
故选：C．
1 ab
7．（4分）若ab1，P lga lgb ，Q (lgalgb)，Rlg ，则( )

2 2
A．RPQ B．PQR C．QPR D．PRQ
第8页 | 共20页ab ab
【解答】解：由平均不等式知 ab  ,lg ab lg( ),QR．
2 2
lgalgb
同理 lga lgb  ,PQ．

2
故选：B．
8．（4分）已知两条直线l :yx，l :ax y0，其中a为实数，当这两条直线的夹角在
1 2

(0, )内变动时，a的取值范围是( )
12
3 3 
A．(0,1) B．( ， 3) C．( ，1) (1， 3) D．(1, 3)
3 3

【解答】解：直线l :yx的倾斜角为 ，令直线l :ax y0的倾斜角为，则有atan
1 4 2

过原点的直线l :yx，l :ax y0的夹角在(0, )内变动时，可得直线l 的倾斜角的
1 2 12 2
    
范围是( ， ) ( ， )．
6 4 4 3
3  3 
l 的斜率的取值范围是( ，1) (1， 3)，即a( ，1) (1， 3)，
2 3 3
故选：C．
9．（4分）一个圆柱的侧面展开图是一个正方形，这个圆柱的全面积与侧面积的比是( )
12 14 12 14
A． B． C． D．
2 4  2
【解答】解：设圆柱底面积半径为r ，则高为2r ，
全面积：侧面积[(2r)2 2r2]:(2r)2
21
 ．
2
故选：A．
10．（4分）过原点的直线与圆x2  y2 4x30相切，若切点在第三象限，则该直线的方
程是( )
3 3
A．y 3x B．y 3x C．y x D．y x
3 3
【解答】解：如图，圆方程为(x2)2  y2 12，
圆心为A(2,0)，半径为1，
1  3
sin , ,tg ．
2 6 3
第9页 | 共20页故选：C．
11．（4分）过抛物线yax2(a0)的焦点F 作一直线交抛物线于P、Q两点，若线段PF
1 1
与FQ的长分别是 p、q，则  等于( )
p q
1 4
A．2a B． C．4a D．
2a a
【解答】解：如图：
1
设PQ直线方程是y kx，
4a
1
则x ，x 是方程ax2 kx 的两根，
1 2 4a
1
p x2 (y  )2  x2 (kx )2 xr，
1 1 4a 1 1 1
其中r  1k2 ．同理qx r．
2
k 1
( )2 4
1 1 pq (x x )r x x (x x )2 4xx a  4a2
从而    2 1  1 2  1 2 1 2  4a．
p q pq xx r2 xx r xx r 1
1 2 1 2 1 2  r
4a2
故选：C．
12．（4分）二项式( 2 33x)50的展开式中系数为有理数的项共有( )
A．6项 B．7项 C．8项 D．9项
r r
25
【解答】解：( 2 33x)50展开式的通项T 2 233Cr xr
r1 50
r r
25
项的系数为2 233Cr
50
要使系数为有理数，需r 是6的倍数
所以r 0，6，12，18，24，30，36，42，48，
第10页 | 共20页故展开式中系数为有理数的项共有9项
故选：D．
二、填空题（共4小题，每小题5分，满分20分）
13．（5分）从含有500个个体的总体中一次性抽取25个个体，假定其中每个个体被抽到的
1
概率相等，那么总体中每个个体被抽到的概率是 ．
20
【解答】解： 含有500个个体的总体中一次性抽取25个个体，

其中每个个体被抽到的概率相等，
25 1
总体中每个个体被抽到的概率是  ，
500 20
1
故答案为： ．
20
x2 y2
14．（5分）椭圆  1的焦点F 、F ，点P为其上的动点，当FPF 为钝角时，点P
9 4 1 2 1 2
3 5 3 5
横坐标的取值范围是 为：( , ) ．
5 5
【解答】解：如图，
设 p(x,y)，则F( 5,0),F ( 5,0)，
1 2
且FPF 是钝角
1 2
 PF2 PF2 FF2 (x 5)2  y2 (x 5)2  y2 20
1 2 1 2
 x2 5 y2 10
x2
 x2 4(1 )5
9
9 3 5 3 5
 x2   x ．
5 5 5
3 5 3 5
故答案为：( , )．
5 5
15．（5分）设{a }是首项为1的正项数列，且(n1)a2 na2 a a 0(n1，2，3，)，
n n1 n n1 n
第11页 | 共20页1
则它的通项公式是a  ．
n n
【解答】解： (n1)a2 na2 a a 0
 n1 n n1 n
1 14n(n1) n
a  a  a （另解a 不合题意舍去），
n1 2(n1) n n1 n n
a a a 1 a 1 1
 2 3 n  ，即 n  ,a  ,n1,2，
a  a  a n a n n n
1 2 n1 1
1
故答案为： ．
n
16．（5分）如图，E、F 分别是正方体的面ADDA 、面BCCB 的中心，则四边形BFDE
1 1 1 1 1
在该正方体的面上的射影可能是 ②③ ．（要求：把可能的图的序号都填上）
【解答】解：因为正方体是对称的几何体，
所以四边形BFDE在该正方体的面上的射影可分为：上下、左右、前后三个方向的射影，
1
也就是在面ABCD、面ABBA、面ADDA 上的射影．
1 1 1 1
四边形BFDE在面ABCD和面ABBA上的射影相同，如图②所示；
1 1 1
四边形BFDE在该正方体对角面的ABCD 内，它在面ADDA 上的射影显然是一条线段，
1 1 1 1 1
如图③所示．故②③正确
故答案为 ②③
第12页 | 共20页三、解答题（共7小题，满分82分）
17．（10分）甲、乙二人参加普法知识竞答，共有10个不同的题目，其中选择题6个，判
断题4个．甲、乙二人依次各抽一题．
（1）甲抽到选择题、乙抽到判断题的概率是多少？
（2）甲、乙二人中至少有一人抽到选择题的概率是多少？
【解答】解：（1）由题意知本题是一个等可能事件的概率，
甲从选择题中抽到一题的可能结果有C1个，乙依次从判断题中抽到一题的可能结果有C1个，
6 4
故甲抽到选择题、乙依次抽到判断题的可能结果有C1C1个；
6 4
试验发生包含的所有事件是甲、乙依次抽一题的可能结果有概率为C1C1个，
10 9
C1C1 4
甲抽到选择题、乙依次抽到判断题的概率为 6 4  ，
C1C1 15
10 9
4
所求概率为 ．
15
（2）甲、乙二人中至少有一人抽到选择题的对立事件是甲、乙二人依次都抽到判断题，
C1C1
甲、乙二人依次都抽到判断题的概率为 4 3 ，

C1C1
10 9
C1C1 13
甲、乙二人中至少有一人抽到选择题的概率为1 4 3  ，
C1C1 15
10 9
13
所求概率为 ．
15
18．（12分）如图，直三棱柱ABCABC ，底面ABC 中，CACB1，BCA90，
1 1 1
棱AA 2，M 、N分别是AB 、AA的中点．
1 1 1 1

（1）求BN 的长；
 
（2）求cos(BA CB)的值；
1 1
（3）求证ABCM ．
1 1
第13页 | 共20页【解答】解：如图，以C为原点建立空间直角坐标系Oxyz．
（1）依题意得B(0，1，0)，N(1，0，1)，

|BN| (10)2 (01)2 (10)2  3（2分）
（2）依题意得A(1，0，2)，B(0，1，0)，C(0，0，0)，B(0，1，2)．
1 1
     
BA (1,1,2)，CB (0,1,2)，BA CB 3，|BA | 6 ，|CB | 5（5分）
1 1 1 1 1 1
 
cos  B  A  C  B   BA 1 CB 1  1 30（9分）
1 1 |  B  A  ||C  B  | 10
1  1
1 1   1 1
（3）证明：依题意得C (0，0，2)，M( , ,2)AB(1，1，2)，CM ( , ,0)，
1 2 2 1 1 2 2
  1 1
 AB CM   00，
1  1 2 2
 
 ABCM （12分）
1 1
19．（12 分）如图，已知平行六面体 ABCDABCD 的底面 ABCD上菱形，且
1 1 1 1
第14页 | 共20页CCBCCDBCD，
1 1
（1）证明：CC BD；
1
CD
（2）当 的值为多少时，能使AC 平面CBD？请给出证明．
CC 1 1
1
【解答】（1）证明：如图，连接AC 、AC和BD交于O，连接CO．
1 1 1
四边形ABCD是菱形，

AC BD，BC CD．
又 BCC DCC ，CC CC，
 1 1 1 1
△CBC △CDC ，
1 1
CBCD，
1 1
DOOB

COBD，（3分）
1
又AC BD，AC COO，
 1
BD平面AC ，
1
又CC平面AC ，
1 1
CC BD．（6分）
1
CD
（2）当 1时，能使AC 平面CBD．
CC 1 1
1
第15页 | 共20页CD
1，

CC
1
BC CDCC，
1
又BCDCCBCCD，
1 1
由此可推得BDCBCD．
1 1
三棱锥CCBD是正三棱锥．（9分）
1
设AC与CO相交于G．
1 1
AC //AC，且AC :OC 2:1，
 1 1 1 1
CG:GO2:1．
1
又CO是正三角形CBD的BD边上的高和中线，
1 1
点G是正三角形CBD的中心，
1
CG平面CBD，
1
即AC 平面CBD．（12分）
1 1
20．（12分）设{a }为等差数列，S 为数列{a }的前n项和，已知S 7，S 75，T 为
n n n 7 15 n
S 
数列 n的前n项和，求T ．
 n  n
【解答】解：设等差数列{a }的公差为d，则
n
1
S na  n(n1)d．
n 1 2
S 7，S 75，
 7 15
7a 21d 7
 1
15a 105d 75.
1
a 3d 1
即 1
a 7d 5.
1
解得a 2，d 1．
1
S 1 1
 n a  (n1)d 2 (n1)，
n 1 2 2
第16页 | 共20页S S 1
n1  n  ，

n1 n 2
S 1
数列{ n}是等差数列，其首项为2，公差为 ，
n 2
1 9
T  n2  n．
n 4 4
21．（12分）设函数 f(x) x2 1ax，其中a0，
（1）解不等式 f(x)„1；
（2）证明：当a…1时，函数 f(x)在区间[0，)上是单调函数．
【解答】（1）解：不等式 f(x)„1即 x2 1„1ax，
由此得1„1ax，即ax…0，其中常数a0．
x2 1„ (1ax)2
所以，原不等式等价于
x…0.
x…0
即 （3分）
(a2 1)x2a…0
2a
所以，当0a1时，所给不等式的解集为{x|0„ x„ }；
1a2
当a…1时，所给不等式的解集为{x|x…0}．（6分）
（2）证明：在区间[0，)上任取x ，x
1 2
使得x x f(x ) f(x ) x2 1 x2 1a(x x )
1 2 1 2 1 2 1 2
x2 x2
 1 2 a(x x )
1 2
x2 1 x2 1
1 2
 
x x
x x  1 2 a9分
1 2  x2 1 x2 1 
 1 2 
x x
1 2 1,且a…1，

x2 1 x2 1
1 2
x x
 1 2 a0，
x2 1 x2 1
1 2
又x x 0，
1 2
第17页 | 共20页f(x ) f(x )0，
1 2
即 f(x ) f(x )．
1 2
所以，当a…1时，函数 f(x)在区间[0，)上是单调递减函数．（12分）
22．（12分）用总长14.8m的钢条制成一个长方体容器的框架，如果所制做容器的底面的一
边比另一边长0.5m，那么高为多少时容器的容积最大？并求出它的最大容积．
【解答】解：设容器底面短边长为xm，则另一边长为(x0.5)m，
14.84x4(x0.5)
高为 3.22x
4
由3.22x0和x0，得0x1.6，
设容器的容积为ym3，则有yx(x0.5)(3.22x)(0x1.6)
整理，得y2x3 2.2x2 1.6x，（4分）
y6x2 4.4x1.6（6分）
令y0，有6x2 4.4x1.60，即15x2 11x40，
4
解得x 1，x  （不合题意，舍去）．（8分）
1 2 15
从而，在定义域(0,1.6)内只有在x1处使y0．
由题意，若x过小（接近0)或过大（接近1.6)时，y值很小（接近0)，
因此，当x1时y取得最大值，y 22.21.61.8，这时，高为3.2211.2．
最大值
答：容器的高为1.2m时容积最大，最大容积为1.8m3．（12分）
8
23．（12分）如图，已知梯形ABCD中|AB|2|CD|，点E分有向线段AC所成的比为 ，
11
双曲线过C、D、E
三点，且以A、B为焦点．求双曲线的离心率．
第18页 | 共20页【解答】解：如图，以AB的垂直平分线为y轴，直线AB为x轴，建立直角坐标系xOy，
则CD y轴．
因为双曲线经过点C、D，且以 A、B为焦点，由双曲线的对称性知C、D关于 y轴对
称．（2分）
c
依题意，记A(c,0)，C( ，h)，B(c,0)，
2
1
其中c为双曲线的半焦距，c |AB|，h是梯形的高．
2
8 c 8
c  0 h
11 2 7 11 8
由定比分点坐标公式，得点E的坐标为x   c，y   h．（5
E 8 19 E 8 19
1 1
11 11
分）
x2 y2 c
设双曲线的方程为  1，则离心率e ．
a2 b2 a
由点C、E在双曲线上，
1 c2 h2
   1
4 a2 b2
得 （10分）
 49 c2 64 h2
 1.
361  a2 361  b2
第19页 | 共20页h2 1 c2 c2
解得  1，化简可得 9，

b2 4 a2 a2
c2
所以，离心率e 3（14分）
a2
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2019/5/27 23:02:56；用户：15217760367；邮箱：15217760367；学号：10888156
第20页 | 共20页