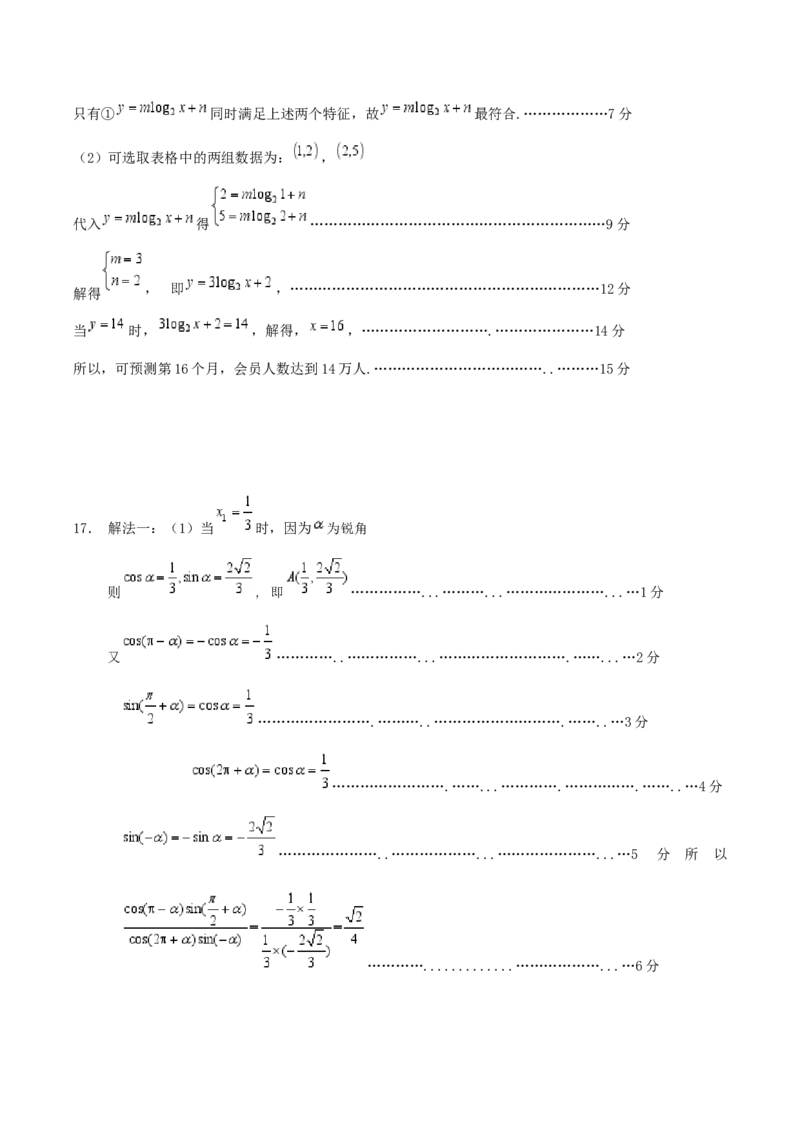文档内容
宁德市2024-2025学年度第一学期期末高一质量检测
数学试题
本试卷共19题.考试时间120分钟,满分150分.
注意事项:
1.答题前考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名,考生要认真核对答题卡上
粘贴的条形码的“准考证号,姓名”与考生本人准考证号、姓名是否一致.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应的题目的答案标号涂黑,如需改动,用橡皮擦干
净后,再选涂其他答案标号;填空题和解答题用0.5毫米黑色签字笔在答题卡上书写作答,在试题卷上作
答,答案无效.
3.考试结束,考生必须将试题卷和答题卡一并交回.
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,有且只有一个是
符合题目要求的.
1.已知命题 ,则命题 的否定是
A. B.
C. D.
2.“ ”是“ ”的
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分不必要条件
3.若幂函数 的图象经过点 ,则 在定义域内为
A.减函数 B.增函数 C.偶函数 D.奇函数
4.已知 ,则
A. B. C. D.5.记 ,设 ,则函数 的最小值是
A.0 B. C. D.2
6.已知函数 的零点为a, , ,则a,b,c的大小关系为
A. B. C. D.
7.已知函数 , ,则图象为如图的函数可能是
A. B.
C. D.
8.定义在 上的函数 满足 ,且 ,则
A. B. 是奇函数
C. 是偶函数 D. 是减函数
二、多项选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中, 有多项是符合
题目要求,全部选对得6分,部分选对得部分分,有选错得0分.
9.已知函数 用列表法表示如下,则下列说法正确的是
A. 的定义域与值域相同
B.
C.若 ,则
D. 是减函数10.已知二次函数 ,则下列说法正确的是
A.当 时, B.当 时,
C.若 恒成立,则 D.若 在 内有零点,则
11.已知桌面上有一个周长为2的由铁丝围成的封闭图形,则
A.当封闭曲线为半圆时,用直径为1的圆形纸片可以完全覆盖
B.当封闭曲线为正六边形时,用直径为1的圆形纸片可以完全覆盖
C.当封闭曲线为平行四边形时,用直径1的圆形纸片不可以完全覆盖
D.当封闭曲线为三角形时,用直径为1的圆形纸片不可以完全覆盖
三、填空题: 本大题共3小题,每小题5分,共15分. 把答案填在答题卡的相应位置.
12.一个扇形的弧长和面积都是 ,则这个扇形的圆心角的弧度数为______.
13. ______.
14. 已知过原点O的直线与函数 的图象交于A,B两点(A点位于B点的左侧),
过A点作x轴的垂线交 的图象于点C,若BC与x轴平行,则A点的坐标为______.
四、解答题:本大题共5小题,共77分. 解答应写出文字说明,证明过程或演算步骤.
15.(本题满分13分)
已知集合 ,集合 .
(1)当 时,求 ;
(2)若 , ,求 的取值范围.16.(本题满分15分)
近几年,直播平台作为一种新型的学习渠道,正逐渐获得越来越多人的关注和喜爱.某平台从2024年初建
立开始,得到了很多网民的关注,会员人数逐月增加,如下表所示:
建立平台第x个月 1 2 3 4 5
会员人数y(万) 2 5 6.7 8 8.9
为了描述从第1个月开始会员人数随时间变化的关系.现有以下三种函数模型供选择:
① ,② ,③ .
(1)选出最符合实际的函数模型,并说明理由;
(2)请选取表格中的两组数据,求出你选择的函数模型的解析式,并预测第几个月会员人数达到14万.
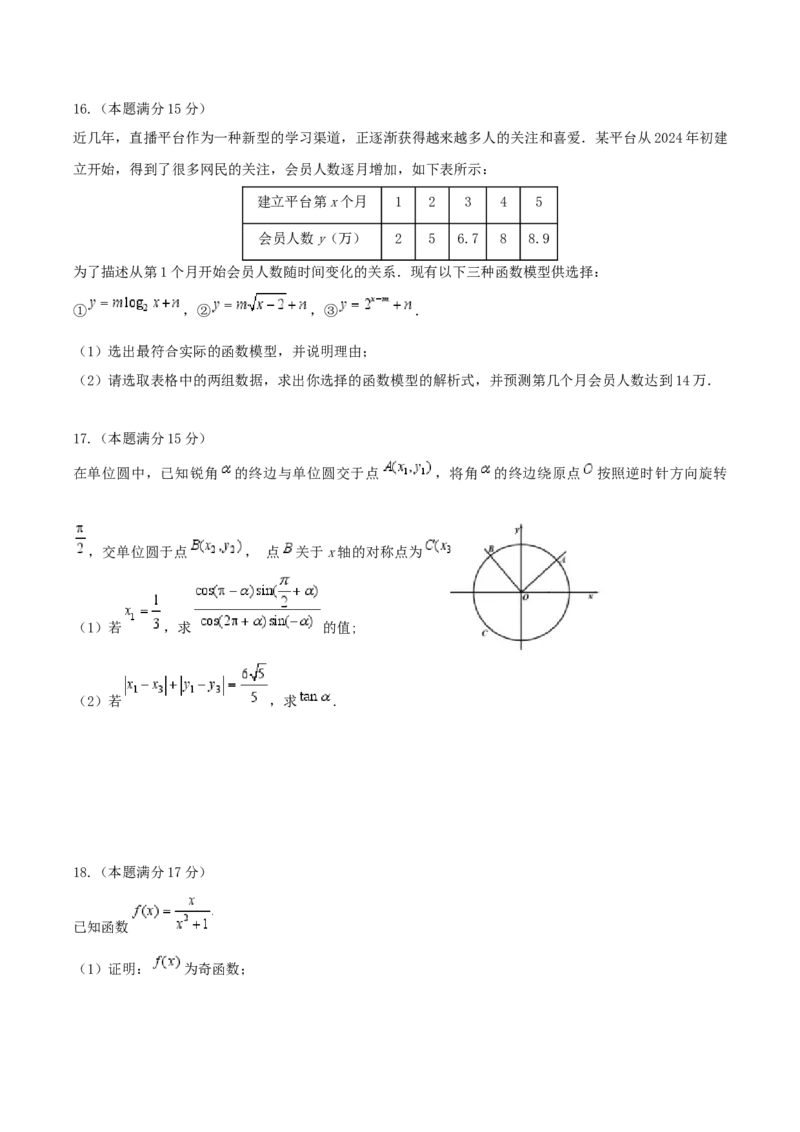
17.(本题满分15分)
在单位圆中,已知锐角 的终边与单位圆交于点 ,将角 的终边绕原点 按照逆时针方向旋转
,交单位圆于点 , 点 关于x轴的对称点为 .
(1)若 ,求 的值;
(2)若 ,求 .
18.(本题满分17分)
已知函数
(1)证明: 为奇函数;(2)讨论函数 在区间 上的单调性;
(3) , ,使得 ,求实数 的取值范围.
19. (本题满分17分)
定义:函数 的定义域为 ,若对 上的任意不同的两个数 和任意的 ,都有
,则称 在 上是凸函数.
(1)判断 是否为凸函数,并说明理由;
(2)已知偶函数 在 上是凸函数,证明: 在 上也是凸函数;
(3)若 在 上是凸函数,对于定义域内任意不同的三个数 和任意的
,证明:当 时,都有
成立.宁德市2024-2025学年度第一学期期末高一质量检测
数学试题参考答案
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,有且只有一个是
符合题目要求的.
1-5. DABDB 6-8 CDB
二、多项选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中, 有多项是符合
题目要求,全部选对得5分,部分选对得部分分,有选错得0分.
9.ACD 10.ACD 11.AB
三、填空题: 本大题共3小题,每小题5分,共15分. 把答案填在答题卡的相应位置
12. 13. 14.
四、解答题:本大题共5小题,共77分. 解答应写出文字说明,证明过程或演算步骤.
15. 解:
(1) ………………………………………………………3分
当 时,
……………..…………………………………5分
所以 …………………………………...…………………………8分
(2)若 时,
……………………………………………..…….………………..…10分
又 .
所以 ……………………………………………..…...………..………………...…12分
所以 的取值范围为 …………………………..…...………..………………...…13分
16.解:
(1)最符合实际的函数模型为① ,………………………………………2分
根据表格知函数解析式需满足在 上有定义,所以② 不满足,…4分
又随着月份的增加,会员人数增加速度又会减慢,所以③ 不符合,………6分只有① 同时满足上述两个特征,故 最符合.………………7分
(2)可选取表格中的两组数据为: ,
代入 得 ………………………………………………………9分
, 即 ,…………………………………………………………12分
解得
当 时, ,解得, ,……………………….…………………14分
所以,可预测第16个月,会员人数达到14万人.………………………………..………15分
17. 解法一:(1)当 时,因为 为锐角
则 , 即 ……………...………...…………………...…1分
又 …………..……………...……………………….……...…2分
…………………….………..……………………….……..…3分
…………………….……...………….…………….……..…4分
…………………..………………...…………………...…5 分 所 以
………….............………………...…6分(2)因为
所 以 ................................................................
…………………………. 7分
则 ......................................................................
…………………..…..8分
所以 ,
又 为锐角
所以
即 .....................................................................
…………………..…9分
....................................……………………………….…………..
…10分
则
即 .
.…………………………………………..……………….…………..…11分
则 …………………………………..……………….…………..…12分
所以 ………………………………..……..………….…………..…13分
即
解得 或 ………………..……………..………….…………..…15分解法二:(1)同解法一
(2)因为
所 以 ..........................................................
…………………………. 7分
则 .................................................................
…………………..…..8分
所以 ,
又 为锐角
所以
即 .................................................................
...………………..…9分
...............................................................…
……………..…10分
联立解得 或 .........................................…………….
…12分
当 时,
.........................................……………………………………….….
.…13分
当 时,
......................................………….………………………..……….
.…14分所以 或 .......………………….……………………………..…15分
18. 解法一:
(1)因为 的定义域为R
所以 为奇函数;……………………………………………………….…………3分
(2) 任取 ,且 ,……………….…….…….…….…………………4分
则 …………….…………………5分
……………………………………..…………7分
因为 ,所以
当 时 ,所以
此时, 在区间 上是增函数;……………………………………..…………8分
当 时 ,所以
此时, 在区间 上是减函数。……………………………………….………9分
综上:函数 在区间 上是增函数,在区间 上是减函数。…………10分
(3)因为 ,所以 ,
,…………………………………………….............................………11分
……………………………………….......................................……………
12分由(2)知,函数 为奇函数,在区间 上是增函数,在区间 上是减函数
又 ,
所以 ,………………………………………….....................………14分
所以, ,整理得 ,解得 …………...…………16分
综上: ……………………………………………………….…………….…..…17分
解法二:(1)(2)同解法一
(3)因为 ,所以 ,
且 ,………………………….....................…………………………11分
由(2)知,函数 为奇函数,在区间 上是增函数,在区间 上是减函数
又 ,所以, ……….......................................……12
分
整理, ,
所以 , …………………………………………....……14分
所以, ,整理得 ,解得 …………...…………16分
综上: ……………………………………………………….…………….…..…17分
19.解:
(1) 是凸函数…………………………………….….…………….…………1分理由如下:
由于 ,所以 ,即 是凸函数. 4分
( 2 ) 任 取 , 所 以 , 因 为 在 上 的 凸 函 数 , 所 以
,················6分
又因为 是偶函数,所以 ,所以 在 上也是凸
函数···································8分
(3)因为 , ,
由对称性不妨设当 时,则 ,
此时 显然成立,·······10分
当 时,因为 在 是凸函数,
所以
··································13分
而 ,再次根据凸函数的定义,
则 · · ·15分
所以
··································17分