文档内容
广东实验中学 2023 届高三级第三次阶段考试
数 学
本试卷分选择题和非选择题两部分,共5页,满分150分,考试用时120分钟。
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考号填写在答题卷上。
2.选择题每小题选出答案后,用2B铅笔把答题卷上对应题目的答案标号涂黑;如需改动,
用橡皮擦干净后,再选涂其它答案;不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内
的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和
涂改液.不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束后,将答题卷收回。
第一部分选择题(共60分)
一、单选题(本大题共8小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1
A={x| ≥1}
1.已知集合
x−2
,
B={x||x−1|<2}
,则
A∩B=
( )
[2,3] [2,3) (2,3) (2,3]
A. B. C. D.
2.若复数z满足
z2 −4z+6=0
,则z=( )
2±√2i 2±√3i −2±√2i −2±√3i
A. B. C. D.
y=2x+1 x2 +y2 −4x+3=0
3.经过直线 上的点作圆 的切线,则切线长的最小值为
( )
√3 √5
A. 2 B. C.1 D.
4.设
a∈N¿
,且
a<27
,且
(27−a)(28−a)
…
(34−a)
等于( )
A8 A 27−a A7 A8
A. 27−a B. 34−a C. 34−a D. 34−
5.以等边三角形ABC为底的两个正三棱锥P-ABC和Q-ABC内接于同一个球,并且正三棱
锥P-ABC的侧面与底面ABC所成的角为45°,记正三棱锥P - ABC和正三棱锥Q-ABC
V
1
=
V
的体积分别为V 和V,则 2 ( )
1 2
1 1 1
2 3 4
A.1 B. C. D.
6.根据《民用建筑工程室内环境污染控制标准》,文化娱乐场所室内甲醛浓度小于等于
0.1mg/m3为安全范围,已知某新建文化娱乐场所施工过程中使用了甲醛喷剂,处于良好
的通风环境下时,竣工 1周后室内甲醛浓度为 6.25mg/m3,3周后室内甲醛浓度为 1
t(t∈N∗)
mg/m3,且室内甲醛浓度 p(t)(单位:mg/m3)与竣工后保持良好通风的时间
1
学科网(北京)股份有限公司ρ(t)=e
at+b
(单位:周)近似满足函数关系式 ,则该文化娱乐场所竣工后的甲醛浓度若
要达到安全开放标准,至少需要放置的时间为( )
A.5周 B.6周 C.7周 D.8周
x
{
,0≤x<1,
m
f(x)=
−x
,−10 P(B)>0 P(B|A)=P(B) |P(A|B)=P(A)
B.己知 , , ,则
ξ P(ξ<2)=0.72 P(1<ξ<2)=0.22
C.设随机变量 服从正态分布N(1,4),且 ,则
D.1,2,3,4,5,6,7,8,9,10的25%分位数为3,90%分位数为9.5
10 . 如 图 , 在 棱 长 为 2 的 正 方 体
ABCD−A
1
B
1
C
1
D
1中 ,
M、N、P
分 别 是
C D 、C C、A A
1 1 1 1
的中点,则( )
A.M,N,B,D 四点共面
1
√10
10
B.异面直线PD 与MN所成角的余弦值为
1
C.平面BMN截正方体所得截面为等腰梯形
1
3
D.三棱锥P- MNB的体积为
11.“圆幂定理”是平面几何中关于圆的一个重要定理,它包含三个结论,其中一个是相
交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.如图,已知圆 O
2
学科网(北京)股份有限公司OP=√2
的半径为2,点P是圆O内的定点,且 ,弦AC,BD均过点P,则下列说法
正确的是( )
A.
⃗PA⋅ ⃗PC
为定值
B.
O⃗A⋅O⃗C
的取值范围是
[−2,0]
C.当
AC⊥BD
时,
⃗AB⋅C⃗D
为定值
D.
AC⊥BD
时,
|
⃗AC|⋅| ⃗BD|
的最大值为12
12.布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它得名于荷兰数学家鲁
f (x)
伊兹·布劳威尔(L.E.J.Brouwer),简单的讲就是对于满足一定条件的连续函数 ,存
x f (x )=x x
在一个点 0,使得 0 0,那么我们称该函数为“不动点”函数,而称 0为该函数
的一个不动点.现新定义:
x f(x )=−x x f (x)
若 0满足 0 0,则称 0为 的次不动点.下列说法正确的是( )
A.定义在R上的偶函数既不存在不动点,也不存在次不动点
B.定义在R上的奇函数既存在不动点,也存在次不动点
1≤a≤ 3 f(x)=log
1
(4x −a⋅2x +1)
2 [0,1]
C.当 时,函数 2 在 上仅有一个不动点和一
个次不动点
√ 1
f (x)= ex − x−a
2 [0,1]
D.满足函数 在区间 上存在不动点的正整数a不存在
第二部分 非选择题(90分)
三、填空题(本大题共4小题,共20分)
1
10
(x+ −y)
x
xy7
13.在 的展开式中, 的系数为 .
2π π
[− , ]
14.已知函数
f(x)=sinωx(ω>0)
在区间
3 3
上单调递增,则ω的取值范围是
.
y2
x2 − =1
a2
15.已知双曲线 ,若过点(2,2)能作该双曲线的两条切线,则该双曲线离心率
e的取值范围为____.
16.某班级在一次植树种花活动中负责对一片圆环区域花圃
栽植鲜花,该圆环区域被等分为n个部分(n≥4),每个
部分从红,黄,蓝三种颜色的鲜花中选取一种进行栽植,
要求相邻区域不能用同种颜色的鲜花,将总的栽植方案数
用a 表示,则a=____,a=____.
n 4 n
3
学科网(北京)股份有限公司四、解答题(本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤)
17.(本小题10分)
{a } n∈N a +a =4n
已知数列 n 中,对任意的 +,都有 n n+1
{a } {a }
(1)若 n 为等差数列,求 n 的通项公式;
a =3 {a }
(2)若 1 ,求 n 的通项公式.
18.(本小题12分)
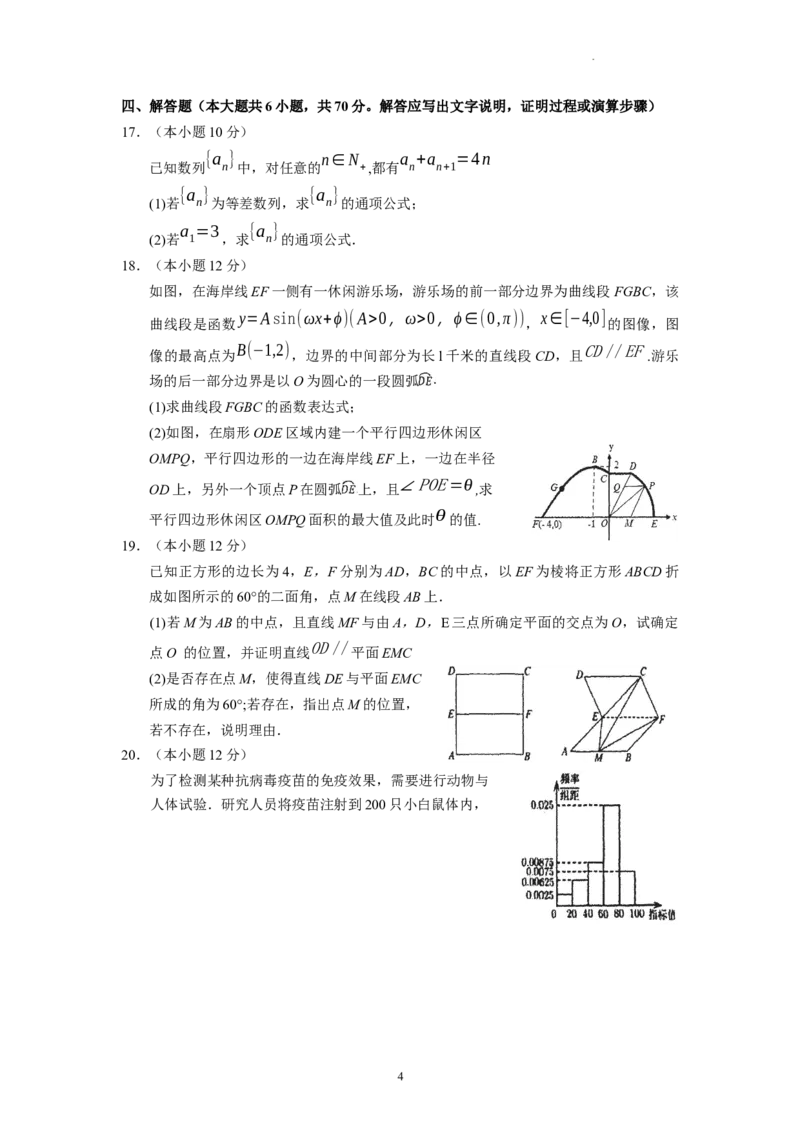
如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该
y=Asin(ωx+ϕ)(A>0,ω>0,ϕ∈(0,π)) x∈[−4,0]
曲线段是函数 , 的图像,图
B(−1,2) CD//EF
像的最高点为 ,边界的中间部分为长l千米的直线段CD,且 .游乐
场的后一部分边界是以O为圆心的一段圆弧
(1)求曲线段FGBC的函数表达式;
(2)如图,在扇形ODE区域内建一个平行四边形休闲区
OMPQ,平行四边形的一边在海岸线EF上,一边在半径
OD上,另外一个顶点P在圆弧
上,且∠POE=θ
,求
θ
平行四边形休闲区OMPQ面积的最大值及此时 的值.
19.(本小题12分)
已知正方形的边长为4,E,F分别为AD,BC的中点,以EF为棱将正方形ABCD折
成如图所示的60°的二面角,点M在线段AB上.
(1)若M为AB的中点,且直线MF与由A,D,E三点所确定平面的交点为O,试确定
OD//
点O 的位置,并证明直线 平面EMC
(2)是否存在点M,使得直线DE与平面EMC
所成的角为60°;若存在,指出点M的位置,
若不存在,说明理由.
20.(本小题12分)
为了检测某种抗病毒疫苗的免疫效果,需要进行动物与
人体试验.研究人员将疫苗注射到200只小白鼠体内,
4
学科网(北京)股份有限公司[0,20),[20,40),[40,60),[60,80),[80,100]
一段时间后测量小白鼠的某项指标值,按 分
组,绘制频率分布直方图如图所示,实验发现小白鼠体内产生抗体的共有 160只,其
中该项指标值不小于60的有110只,
假设小白鼠注射疫苗后是否产生抗体相互独立.
(1) 填写下面的2×2列联表,并根据列联表及
指标值
a=0.05
的独立性检验,判断能否认为注射疫 抗体 合计
小于60 不小于60
苗后小白鼠产生抗体与指标值不小于60有关.
有抗体
(单位:只)
(2)为检验疫苗二次接种的免疫抗体性,对第一次 没有抗体
注 射疫苗后没有产生抗体的40只小白鼠进行 合计
第二次注射疫苗,结果又有20只小自鼠产生 抗
体.
(i)用频率估计概率,求一只小白鼠注射2次疫苗后产生抗体的概率p;
(ii)以(i)中确定的概率p作为人体注射2次疫苗后产生抗体的概率,进行人体接种试验,
记n个人注射2次疫苗后产生抗体的数量为随机变量X.试验后统计数据显示,当X
=99时,P(X)取最大值,求参加人体接种试验的人数n.
n(ad−bc) 2
x2
=
(a+b)(c+d)(a+c)(b+d)
参考公式: (其中n=a+b+c+d为样本容量)
P(x2 ≥k ) 0.50 0.40 0.25 0.15 0.100 0.050 0.025
0
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024
0
21.(本小题12分)
C:y2 =2px(p>0)
已知抛物线 的焦点F到准线的距离为2,圆M与y轴相切,且圆
心M与抛物线C的焦点重合.
(1)求抛物线C和圆M的方程;
P(x ,y )(x =¿2)¿
(2)设 0 0 0 为圆M外一点,过点P作圆M的两条切线,分别交抛物线C
A(x ,y ),B(x ,y ) Q(x ,y ),R(x ,y ) y y y y =16,
于两个不同的点 1 1 2 2 ,和点 3 3 4 4 ,且 1 2 3 4 证
明:点P在一条定曲线上.
22.(本小题12分)
f(x)=alnx−2x(a=¿0)¿
已知函数
f (x)
(1)讨论 的单调性;
xa
−2f(x)≥cos[f(x)]
(2)当
x>0
时,不等式e
2x
恒成立,求a的取值范围.
5
学科网(北京)股份有限公司数学参考答案
一、单选1.C 2.A 3.A 4.D 5.D 6.B 7.C 8.B
二、多选9.BCD 10.BCD 11.ACD 12.BC
3
√21
(0, ) (1,√2)∪(√2, )
4 3 2n +2⋅(−1) n
三、填空13.-360 14. 15. 16.18,
四、解答
a +a =4n a +a =4 a +a =8
17.解:方法一:(1)由条件 n n+1 ,可得: 1 2 , 2 3 ……1
分
{a } a =1,d=2
因为 n 为等差数列,设公差为d,由上式可得: 1 ……3分
∴{a } a =a +(n−1)d=2n−1
n 的通项公式为 n 1 ……5分
{a } a =a +(n−1)d a =a +nd
方法二:因为 n 为等差数列,设 n 1 ,则 n+1 1
a +a =2a +(2n−1)d=(2a −d)+2nd
n n+1 1 1 ……1分
又
a
n
+a
n+1
=4
n,所以
2a
1
−d=0
,
2d=4
,解得
d=2,a
1
=1
……3分
∴{a } a =a +(n−1)d=2n−1
n 的通项公式为 n 1 ……5分
a +a =4n a +a =4(n+1)
(2)由条件 n n+1 ,可得: n+1 n+2
a −a =4
两式相减得: n+2 n ……7分
a =3 a =1 {a }
因为 1 ,所以 2 ,数列 n 的奇数项是首项为3,公差为4的等差数列;
a =a +(k−1)d=4k−1
2k−1 1 ……8分
6
学科网(北京)股份有限公司a =a +(k−1)d=4k−3
偶数项是首项为1公差为4的等差数列. 2k 2 ……9分
a =¿{2n+1,n为奇数 ¿¿¿¿
n
综上: ……10分
T
∵ =3
4
18.解:(1)由己知条件,得A=2,……1分 又 ,
2π π
T= =12 ∴ω=
ω 6
……2分
π 2π
y=2sin(− +ϕ)=2 ∴ϕ=
又∵当
x=−1
时,有
6
,且
ϕ∈(0,π) 3
……3分
π 2π
y=2sin( x+ )
6 3 x∈[−4,0]
∴曲线段FGBC的解析式为 , ……5分(没有定义域扣1
分)
π
∴OD=2,∠COD=
OC=√3,CD=1
6
(2)如图, , ……6分
PP ⊥x RtΔOpp pp=OPsinθ=2sinθ
作 1 轴于P 点,在 1中: 1
1
OP OM
=
2π π
sin sin( −θ)
ΔOMP 3 3
在 中,
π
OPsin( −θ)
3 2√3
∴OM= =2cosθ− sinθ
2π 3
sin
3.
……8分
2√3
S =OM⋅PP =(2cosθ− sinθ)×2sinθ
ompq 1 3
……9分
4√3 2√3 2√3
=4sinθcosθ− sin2θ=2sin2θ+ cos2θ−
3 3 3
4√3 π 2√3 π
= sin(2θ+ )− ,θ∈(0, )
3 6 3 3
……11分
π n π 2√3
2θ+ = θ=
6 2 6
当 时,即 时,平行四边形面积有最大值为 3 (平方千米) ……l2分
19.解:(1)∵直线
MF⊂平面
ABFE,故点 O 在平面
ABFE
内也在平面ADE内,∴点O在平面ABFE与平面ADE的交
线上,延长FM交EA的延长线于O,……1分
∵AO//BF ,M为AB的中点,∴ΔOAM≃ΔFBM
7
学科网(北京)股份有限公司∴OM=MF
,
AO=BF
,所以点O在EA的延长线上,
且AO=2,……2分
连接DF交EC于N,因为四边形CDEF为矩形,
∴N
是FD的中点,连接MN,因为MN为△DOF
的中位线,∴MN//OD
……3分
又∵MN⊂平面EMC, OD {⊂¿
平面EMC ……3分
OD//
∴直线 平面EMC. ……5分
(2)由己知可得,
EF⊥AE
,
EF⊥DE
∴∠DEA
为二面角,D-EF-A 的平面角,
∠DEA=60o
,
EF⊥¿¿平面
ADE,又 EF⊂平面
ABFE,
∴平面ABFE¿平面ADE.
作
DH⊥AE
于H,则
DH⊥¿¿平面AEFB,易得H为AE中点
……6分
以H为坐标原点,以HA,HD所在直线分别为x轴,z轴,建立如图所示的空间直角坐标
E(−1,0,0) D(0,0,√3) C(0,4,√3) F(−1,4,0) ⃗ED=(1,0,√3) ⃗EC=(1,4,√3)
系, , , , ,所以 ,
M(1,t,0)(0≤t≤4) ⃗EM=(2,t,0)
设 ,则
{
⃗m⋅
⃗EM
=0 ¿ ¿ ¿ ¿
⃗m=(x,y,z)
设平面EMC的法向量 ,则
8−t 8−t
z= ⃗m=(t,−2, )
取y=﹣2,则x=t, √3 ,所以 √3 ……8分
∵DE
与平面EMC所成的角为60°,
8
∴sin60°=|cos⟨⃗ED,⃗m⟩|=
√
2 t2 +4+
(8−t) 2
3
∴ ……10分
2√3 √3
∴ = ,∴t2 −4t+3=0
√ t 2 −4t+19 2 ,得 t=1 或 t=3 ,
即M为线段AB的三等分点. ……11分
∴存在线段AB的三等分点M,使得直线DE与平面EMC所成的角为60°. ……12分
20.解:(1)由频率分布直方图,知200只小白鼠按指标值分布为:
[0,20) [20,40)
在 内有0.0025×20×200=10(只);在 内有 0.00625×20×200 = 25(只);
[40,60) [60,80)
在 内有 0.00875 ×20×200 = 35(只);在 内有 0.025×20×200 = 100(只)
8
学科网(北京)股份有限公司[80,100]
在 内有0.0075×20×200=30(只).
由题意,有抗体且指标值小于60的有50只;而指标值小于60的小白鼠共有10+25+35=70
只,所以指标值小于60且没有抗体的小白鼠有20只,
指标值
抗体 合计
同理,指标值不小于60且没有抗体的小白鼠有20只, 小于60 不小于60
故列联表如下:单位:只 ……2分 有抗体 50 110 160
H 没有抗体 20 20 40
零假设为 0:注射疫苗后小白鼠产生抗体与指标值不
合计 70 130 200
小于60无关联.
200×(50×20−20×110) 2
x2 = ≈4.945>3.841=x
根据列联表中数据,得 160×40×70×130 0.05 ……4
分
根据
α=0.05
的独立性检验,推断
H
0不成立,即认为注射疫苗后小白鼠产生抗体与指标
值不小于60有关,此推断犯错误的概率不大于0.05 ……5分
(2)(i)令事件A=“小白鼠第一次注射疫苗产生抗体”,事件 B=“小白鼠第二次注射疫苗产生
抗体’’,事件C=“小白鼠注射2次疫苗后产生抗体”
P(A),P(B),P(C),
记事件A,B,C发生的概率分别为
160 20
P(A)= =0.8 P(B|A)= =0.5
200 40
则 , ……6分
P(C)=1−P(AB)=1−P(A)P(B|A)=1−0.2×0.5=0.9.
p=0.9
所以一只小白鼠注射2次疫苗后产生抗体的概率 ……8分
X~B(n,0.9) P(X=k)=Ck ×0.9k ×0.1n−k (k=0,1,2,⋅¿⋅,n)
(ii)由题意,知随机变量 , n
{C9
n
9 ×0.999 ×0.1n−99 ¿C 9
n
8 ×0.9 98 ×0.1 n−98
P(X=99) C 99 ×0.9 99 ×0.1 n−99 ¿C 100 ×0.9 100 ×0.1 n−100
因为 最大,所以 n n ……9分
1
109≤n≤110 ,
9
解得 ……11分
∵n是整数,所以
n=109
或
n=110,
∴接受接种试验的人数为109或110.……12分
21.解:(1)由题设得P=2 ……1分∴抛物线C的方程为 y2 =4x, ……2分
F(1,0) (1,0)
因此,抛物线的焦点为 ,即圆M的圆心为M
(x−1) 2 +y2 =1
由圆M与y轴相切,所以圆M半径为1,所以圆M的方程为 ……4分
P(x ,y )(x =¿2)¿ x =¿0.¿
(2)证明:由于 0 0 0 ,每条切线都与抛物线有两个不同的交点,则 0
y−y =k(x−x ) kx−y+y −kx =0
故设过点P且与圆M相切的切线方程为 0 0 ,即 0 0
9
学科网(北京)股份有限公司|k+y −kx|
0 0
=1
依题意得
√k2 +1
……5分
x (x −2)k2 −2y (x −1)k+y2 −1=0
整理得 0 0 0 0 0 ①;……6分
k ,k k ,k
设直线PA,PQ的斜率分别为 1 2,则 1 2是方程①的两个实根,
2y (x −1) y2 −1
k +k = 0 0 k ⋅k = 0
1 2 x (x −2) 1 2 x (x −2)
故 0 0 , 0 0 ②, ……7分
{kx−y+y −kx =0
0 0
y2 =4x ky2 −4 y+4(y −kx )=0
由 ,得 0 0 ③
A(x ,y ),B(x ,y ) Q(x ,y ),R(x ,y )
因为点 1 1 2 2 , 3 3 4 4
4(y −k x ) 4(y −k x )
y y = 0 1 0 y y = 0 2 0
1 2 k 3 4 k
则 1 ④, 2 ⑤,……9分
由 ② , ④ , ⑤ 三 式 得
16(y −k x )(y −k x ) 16[y2 −(k +k )x y +x2k k ]
y y y y = 0 1 0 0 2 0 = 0 1 2 0 0 0 1 2
1 2 3 4 k k k k
1 2 1 2
[ 2y (x −1) ]
16 y2 0 0 x y
16[ y2 −(k +k )x y ] 0 x (x −2) 0 0
= 0 1 2 0 0 +16x2 = 0 0 +16x2 =16
k k 0 y2 −1 0
1 2 0
x (x −2)
0 0 ……1 0分
y2x (x −2)−2y (x −1)x y =(1−x2 )(y2 −1)
即 0 0 0 0 0 0 0 0 0 ,
y2x2 −2 y2x −2 y2x2 +2x y2 =y2 −x2 y2 −1+x2, x2 +y2 =1
则 0 0 0 0 0 0 0 0 0 0 0 0 即 0 0
x2 +y2 =1
所以点P在圆 ……l 2分
a
f' (x)= −2
f (x) (0,+∞) x
22.解:(1)由题意 的定义域为 ,又 ……1分
a
f' (x)= −2<0
x f (x) (0,+∞)
当a<0时,因为x>0,所以 ,故 在 上单调递减;……2分
a a
f' (x)= −2=0 x=
x 2
当a>0时,令 ,解得:
a a
x∈(0, ) (0, )
当
2
时,
f' (x)>0
,故
f (x)
在
2
上单调递增,
a a
x∈( ,+∞) ( +∞)
当
2
时,
f' (x)<0
,故
f (x)
在
2
上单调递减,……3分
f (x) (0,+∞)
综上所述,当a<0时,函数 的单调递减区间为
10
学科网(北京)股份有限公司a a
(0, ) ( +∞),
f (x) 2 2
当a>0时,函数 的单调递增区间为 ,单调递减区间为 ……4分
xa
−2f(x)≥cos[f(x)]⇔ealnx−2x −2f(x)−cos[f(x)]≥0¿
(2)e
2׿
⇔ef(x) −2f(x)−cos[f(x)]≥0
……6分
g(t)=et −2t−cost t=f (x) g' (t)=et −2+sint,
设 ,其中 ,则
h(t)=et +sint−2, h' (t)=et +cost,
设 则
当
t≤0
时,
et ≤1
,
sint≤1
且等号不同时成立,则
g' (t)<0
恒成立;……7分
当
t>0
时,
et >1
,
cost≥−1
则
h' (t)>0
恒成立,则
g' (t)在 (0,+∞)
上单调递增,
又因为
g' (0)=−1
,
g' (1)=e−2+sin1>0
,所以,存在
t
0
∈(0,1)
使得
g' (t
0
)=0
当
0t
0时,
g' (t)>0.
g(t) (−∞,t ) (t ,+∞) g(0)=0
所以,函数 在 0 上单调递减,在 0 上单调递增,且 ……9
分
g(t)
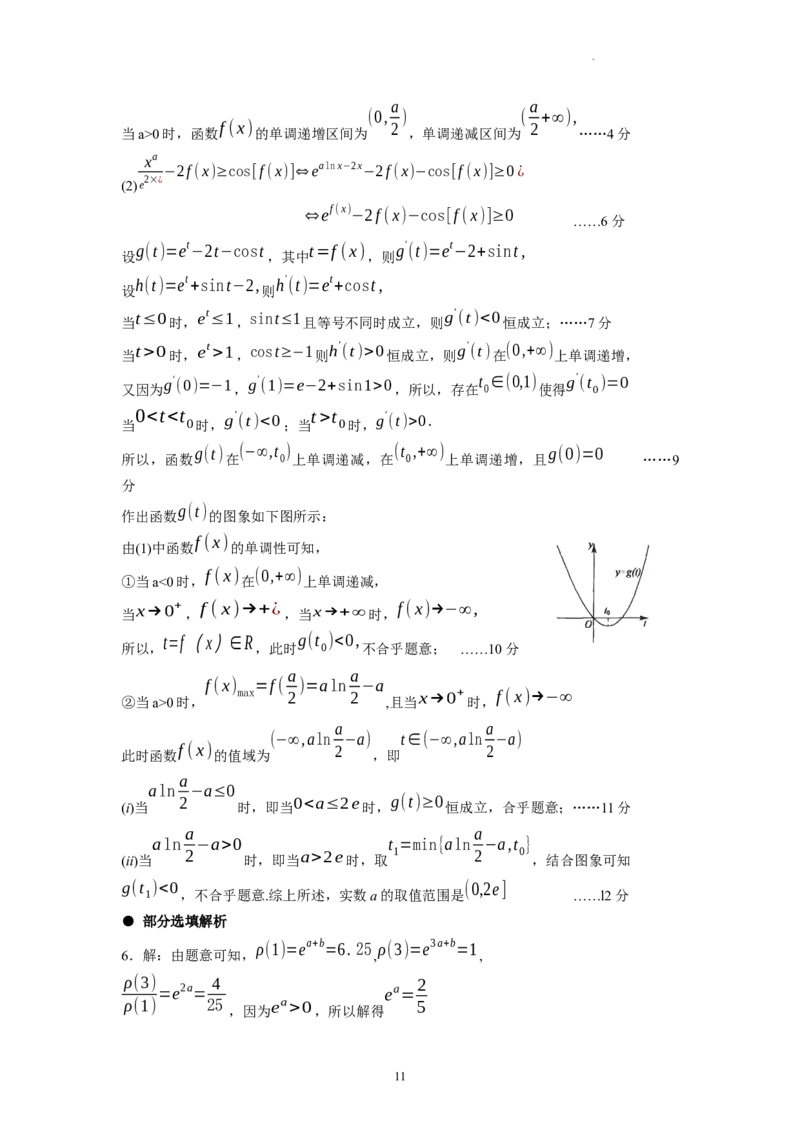
作出函数 的图象如下图所示:
f (x)
由(1)中函数 的单调性可知,
f (x) (0,+∞)
①当a<0时, 在 上单调递减,
当
x→0+
,
f (x)→+¿
,当x→+∞时,
f (x)→−∞,
t=f(x)∈R g(t )<0,
所以, ,此时 0 不合乎题意; ……10分
a a
f(x) =f( )=aln −a
②当a>0时,
max 2 2
,且当
x→0+
时,
f (x)→−∞
a a
(−∞,aln −a) t∈(−∞,aln −a)
f (x) 2 2
此时函数 的值域为 ,即
a
aln −a≤0
(i)当
2
时,即当
00 t =min{aln −a,t }
(ii)当
2
时,即当
a>2e
时,取
1 2 0
,结合图象可知
g(t )<0 (0,2e]
1 ,不合乎题意.综上所述,实数a的取值范围是 ……l2分
● 部分选填解析
ρ(1)=ea+b =6.25 ρ(3)=e3a+b =1
6.解:由题意可知, , ,
ρ(3) 4 2
=e2a = ea =
ρ(1) 25
,因为
ea >0
,所以解得
5
11
学科网(北京)股份有限公司设该文化娱乐场所竣工后放置t 周后甲醛浓度达到安企开放标准,
0
ρ(t )=e at 0 +b =ea+b ¿e a(t 0 −1) =6.25×( 2 ) t 0 −1 ¿0.1
0 5
则
5 −1 5 5 5
62.5≤( ) t0 62.5=( ) m−1, ( ) 4 <62.5<( ) 5
2 2 2 2
整理得 ,设 因为
所以
40,¿
,∴由 均为锐角,得
sinα cosβ sinβcosβ tanβ 1 1 √2
∴tana= = = = = ≤ = ,
cosα 1 sin2β+1 2tan2β+1 1 2√2 4
sinβ+ 2tanβ+
sinβ tanβ
√2
tanβ=
当且仅当 2 时等号成立.
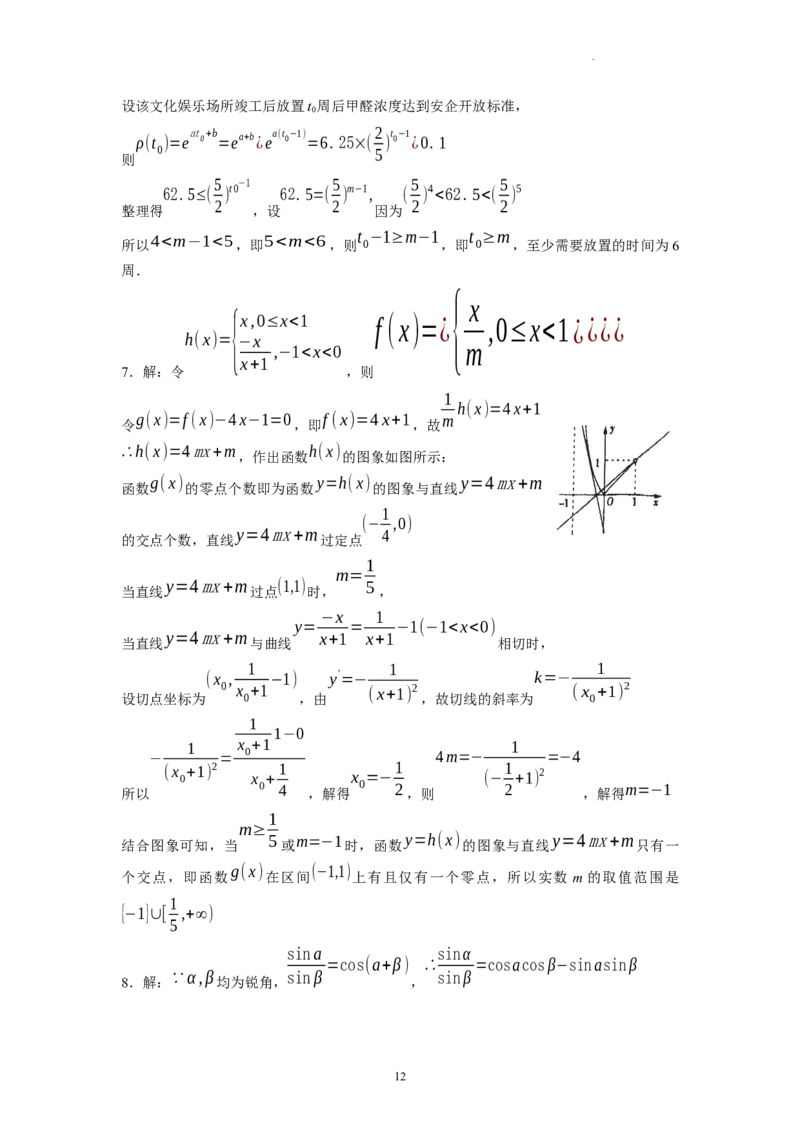
10.解:对于A,易知MN与BD 为异面直线,所以M,N,B,D 不可能四点共面,故A
1 1
MN//CD ∠PD C
错误;对于B,连接CD,CP,易得 1,所以 1 为异面直线PD 与MN所成
1 1
角,∵AB=2则
CD
1
=2√2,D
1
P=√5,PC=3
,
(2√2) 2 +(√5) 2 −32 √10
∴cos∠PD C= =
1 2×2√2×√5 10
√10
PD 10
所以异面直线 1与MN所成角的余弦值为 ,故B正确.
A B,A M, A B//MN
对于C,连接 1 1 ,易得 1 ,所以平面BMN截正
方体所得,
MNBA ,
截面为梯形 1 故C正确;
对于 D,易得
D
1
P//BN
,因为
D
1
P⊄
平面 MNB,
MN⊂平面
MNB,所以
D
1
p//
平面
MNB,
1 1 1
V = × ×1×1×2= ,
所以 V P−MNB =V D 1 −MNB = B−MND 1 3 2 3 故D正确.
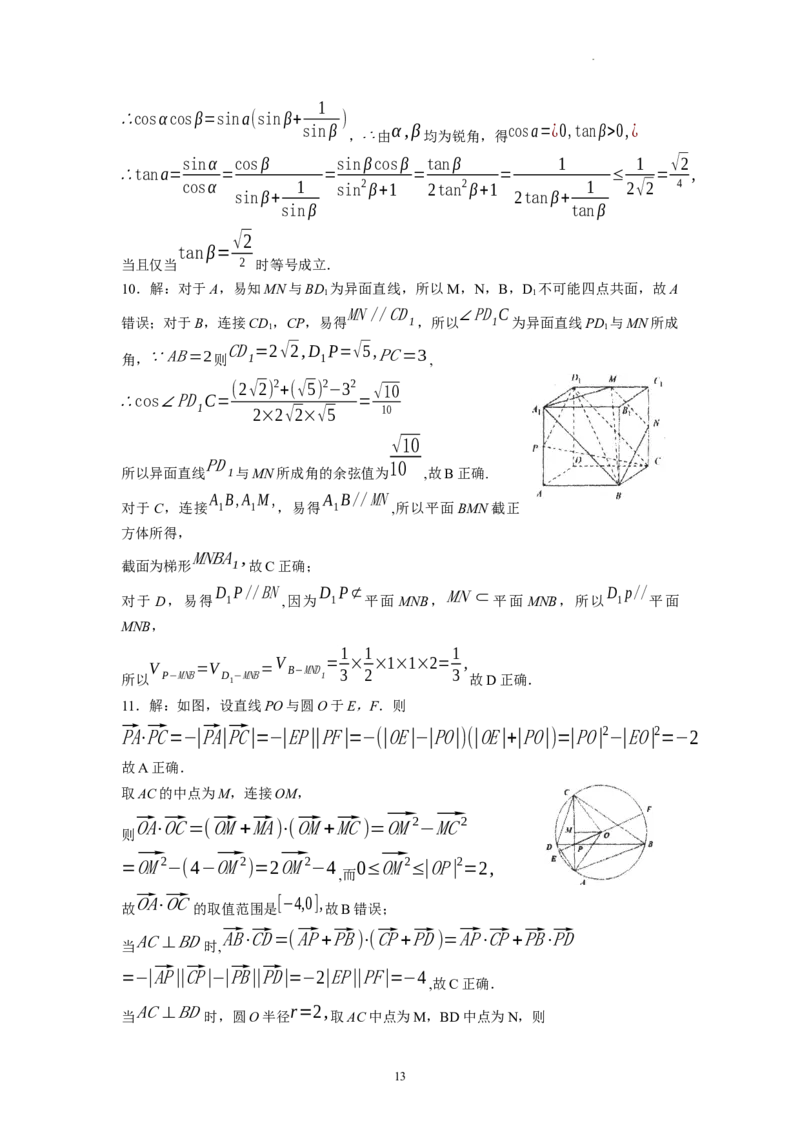
11.解:如图,设直线PO与圆O于E,F.则
⃗PA⋅ ⃗PC=−| ⃗PA| ⃗PC|=−|EP||PF|=−(|OE|−|PO|)(|OE|+|PO|)=|PO| 2 −|EO| 2 =−2
故A正确.
取AC的中点为M,连接OM,
O⃗A⋅O⃗C=(O⃗M+ ⃗MA)⋅(O⃗M+ ⃗MC)= ⃗ OM2
−
⃗ MC2
则
= ⃗ OM2 −(4− ⃗ OM2 )=2 ⃗ OM2 −4 0≤ ⃗ OM2 ≤|OP| 2 =2,
,而
故
O⃗A⋅O⃗C
的取值范围是
[−4,0],
故B错误;
当
AC⊥BD
时,
⃗AB⋅C⃗D=( ⃗AP+ ⃗PB)⋅(C⃗P+ ⃗PD)= ⃗AP⋅C⃗P+ ⃗PB⋅ ⃗PD
=−|
⃗AP||C⃗P|−| ⃗PB|| ⃗PD|=−2|EP||PF|=−4
,故C正确.
当
AC⊥BD
时,圆O半径
r=2,
取AC中点为M,BD中点为N,则
13
学科网(北京)股份有限公司( 4−|O⃗M| 2 +4−| ⃗ ON2 | )
| ⃗AC| 2 | ⃗BD| 2 =4(r2 −|O⃗M| 2 )⋅4(r2 −|O⃗N| 2 )≤16 =4⋅(8−2) 2 =144
4
| O⃗M | 2 +| O⃗N | 2 =| O⃗P | 2 =2
最 后 等 号 成 立 是 因 为 , 不 等 式 等 号 成 立 当 且 仅 当
|O⃗M| 2 =|O⃗N| 2 =1
,故D正确.
f (x)=x2,f (0)=0 f (x) f (x)
12.解:对于选项A:取函数 ,0既是 的不动点,又是
f(0)=0,
的次不动点,故选项A错;对于选项B,定义在R上的奇函数满足
故选项B正确;
1 1 1
log (4x −a⋅2x +1)=x ∴4x −a⋅2x +1= a=2x + −
1 2x 2x 22x
对于选项C:当 2 时, 即
1 1
∴a=t−+ −
令
2x =t
,
t∈[1,2]
,
t t2
在区间
[1,2]
单调递增,
1 1
a=2x
+ −
2x 22x [0,1]
在 单调递增,
log
1
(4x −a⋅2x +1)=x 1≤a≤ 9
4
满足 2 有唯一解,则
log (4x −a⋅2x +1)=−x a=2x + 1 −1
1
当 2
时,∴4x −a⋅2x +1=2x
,即
2x
1 1
∴a=t+ −1 a=2x + −1
令
2x =t
,
t∈[1,2] t
在区间
[1,2]
单调递增,
2x
在
[0,1]
log
1
(4x −a⋅2x +1)=−x 1≤a≤ 3 , 1≤a≤ 3 ,
2 2
单调递增,满足 2 有唯一解,则 ,于是
故选项C正确;对于选项D:
√ 1
f (x)= ex − x−a
2 [0,1] f (x)=x [0,1]
∵函数 在区间 上存在不动点,则 在 上有解,
1 1 1
a=ex − x−x2 m(x)=ex − x−x2 m' (x)=ex − −2x
2 [0,1] 2 2
则 在 上有解,令 ,则
1
n(x)=ex − −2x
再令
2
,则
n' (x)=ex −2=0
,解得
x=ln2
∴n(x) (0,1n2) (ln2,1)
在 上单调递减,在 上单调递增,
3
1 3
∴n(x) =n(1n2)=2− −2ln2= −2ln2=lne2 −ln4=ln√e3 −ln√16>0
min 2 2
∴m(x)>0 [0,1] m(x) [0,1]
在 上恒成立,所以 在 上单调递增,
14
学科网(北京)股份有限公司3
m(x) =m(1)=e− ,
∴m(x)min=m(0)=1 max 2
,
3
1≤a≤e−
∴实数a满足
2
(e为自然对数的底数),正整数
a=1
,故选项D错误
4 4
4− <1 a2 <
a2 3
15.解:过(2,2)能作两条切线说明该点在双曲线外部,故 ,故
7 √21
∴e2 =1+a2
< ∴e<
3 , 3 又点不在该双曲线渐近线上,故 a=¿1¿ ,即 e=¿√2,¿
√21
e∈(1,√2)∪(√2, )
综上, 3
16.解:①当n=4时,第1区域有3种选择,第2区域有2种选择,
∵第4区域要与第1区域颜色不同,故对第3区域的选择分类讨论:
当第3区域与第1区域颜色相同时,第4区域有2种选择;
当第3区域与第1区域颜色不同时,第4区域仅有1种选择,
∴a =3×2×(2+1)=18
4
n(n≥4)
②当将圆分成 个区域,用3种不同颜色给每一个区域染色时,第1区域有3种染
色方案,
第2区域至第n-1区域有2种染色方案,此时考虑第n区域也有2种涂色方案,在此情况
下有两种情况:
情况一:第n区域与第1区域同色,此时相当于将这两区域重合,这时问题转化为用 3种
a
不同颜色给圆上n-1个区域涂色,且相邻区域颜色互异,即为 n−1种染色方案;
情况二:第n区域与第1区域不同色,此时问题就转化为用3种不同颜色给圆上n个区域
染色,且相邻区域颜色互异,即此时的情况就是a,
n
3⋅2n−1 =a +a −1 a =18
根据分类原理可知 n n ,且满足初始条件: 4
{a =3⋅2n−1 −a
n n−1
a =18 a =3⋅2n−1 −a a −2n =−(a −2n−1 )
即递推公式为 4 , n n−1,变形得 n n−1
{a −2n } ∴a −2n =(a −24 )(−1) n−4
∴数列 n 是以-1为公比的等比数列, n 4
a =2n +(18−16)(−1) n−4 =2n +2⋅(−1) n 2n +2⋅(−1) n.
即 n ,故答案为:18,;
15
学科网(北京)股份有限公司