文档内容
A级:“四基”巩固训练
一、选择题
1.某企业2016年12月份的产值是2016年1月份产值的P倍,若2016年每
月产值的平均增长率均相同,则该企业2016年每月产值的平均增长率为( )
A. B.-1
C. D.
答案 B
解析 设2016年1月份产值为 a,每月产值的平均增长率为 x,则aP=a(1
+x)11,∴x=-1.
2.某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为 y=其中
x代表拟录用人数,y代表面试人数,若面试人数为60,则该公司拟录用人数为(
)
A.15 B.40
C.25 D.130
答案 C
解析 若4x=60,则x=15>10,不符合题意;若2x+10=60,则x=25,
满足题意;若1.5x=60,则x=40<100,不符合题意.故拟录用25人.
3.下列函数关系中,可以看作是指数型函数y=kax(k∈R,a>0且a≠1)的模
型的是( )
A.竖直向上发射的信号弹,从发射开始到信号弹到达最高点,信号弹的高
度与时间的关系(不计空气阻力)
B.我国人口年自然增长率为1%时,我国人口总数与年份的关系
C.如果某人t s内骑车行进了1 km,那么此人骑车的平均速度v与时间t的
函数关系
D.信件的邮资与其重量间的函数关系
答案 B
解析 A中的函数模型是二次函数;B中的函数模型是指数型函数;C中的
函数模型是反比例函数;D中的函数模型是一次函数.故选B.
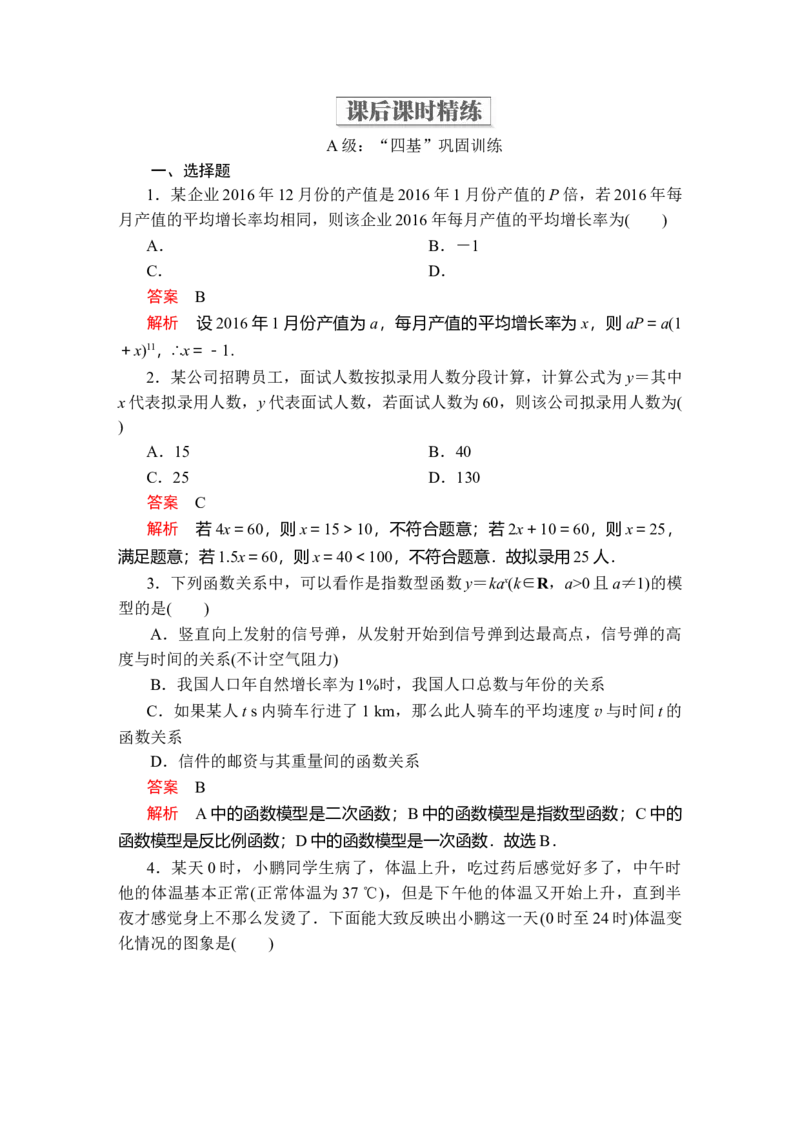
4.某天0时,小鹏同学生病了,体温上升,吃过药后感觉好多了,中午时
他的体温基本正常(正常体温为37 ℃),但是下午他的体温又开始上升,直到半
夜才感觉身上不那么发烫了.下面能大致反映出小鹏这一天(0时至24时)体温变
化情况的图象是( )答案 C
解析 观察图象A,体温逐渐降低,不符合题意;图象B不能反映“下午他
的体温又开始上升”;图象D不能体现“下午他的体温又开始上升”与“直到
半夜才感觉身上不那么发烫了”.综上所述,只有图象C是正确的.
5.某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y
=ekx+b(e=2.718…为自然对数的底数,k,b为常数).若该食品在0 ℃的保鲜时
间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是(
)
A.16小时 B.20小时
C.24小时 D.21小时
答案 C
解析 由题意,知解得当x=33时,y=e33k+b=(e11k)3·eb=3×192=24(小时).
二、填空题
6.某公司在甲、乙两地销售同一种品牌车,利润(单位:万元)分别为L =
1
5.06x-0.15x2和L =2x,其中x为销售量(单位:辆).若该公司在这两地共销售
2
15辆车,则能获得的最大利润为________万元.
答案 45.6
解析 设甲地销售 x辆,则乙地销售(15-x)辆,所以总利润为 S=5.06x-
0.15x2+2(15-x)=-0.15x2+3.06x+30=-0.15(x-10.2)2+45.606(x∈N*).
所以当x=10时,总利润取得最大值,S =45.6(万元).
max
7.某种型号的汽车紧急刹车后滑行的距离 y(km)与刹车时的速度 x(km/h)的
关系可以用y=ax2来描述,已知这种型号的汽车在速度为 60 km/h时,紧急刹车
后滑行的距离为b km.若一辆这种型号的汽车紧急刹车后滑行的距离为3b km,
则这辆车的行驶速度为________km/h.答案 60
解析 由题意得 a×602=b,解得 a=,所以 y=x2.因为 y=3b,所以 x2=
3b,解得x=-60(舍去)或x=60,所以这辆车的行驶速度是60 km/h.
8.衣柜里的樟脑丸随着时间会挥发而体积变小,刚放进的新丸体积为a,经
过t天后体积V与天数t的关系式为V=ae-kt,新丸经过50天后,体积变为A.
若一个新丸体积变为a,则需经过________天.
答案 75
解析 由题意,得a=ae-50k,解得e-25k=.令ae-kt=a,即e-kt=3=(e-25k)3=e
-75k,即需经过的天数为75.
三、解答题
9.某地区为响应上级号召,在 2017年初,新建了一批有200万平方米的廉
价住房,供困难的城市居民居住.由于下半年受物价的影响,根据本地区的实际
情况,估计今后廉价住房的年平均增长率只能达到5%.
(1)经过x年后,该地区的廉价住房为 y万平方米,求y=f(x)的表达式,并求
此函数的定义域;
(2)作出函数y=f(x)的图象,并结合图象,求经过多少年后,该地区的廉价住
房能达到300万平方米?
解 (1)经过1年后,廉价住房面积为
200+200×5%=200(1+5%);
经过2年后为200(1+5%)2;
…
经过x年后,廉价住房面积为200(1+5%)x,
∴y=200(1+5%)x(x∈N*).
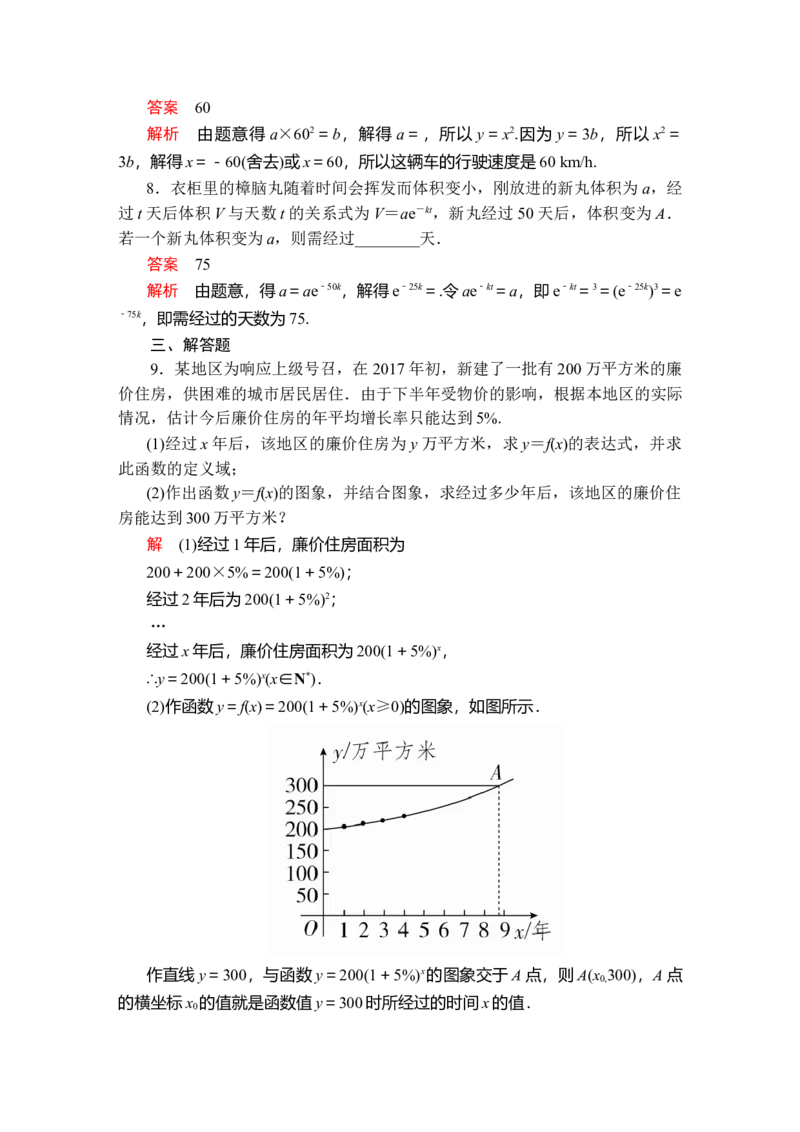
(2)作函数y=f(x)=200(1+5%)x(x≥0)的图象,如图所示.
作直线y=300,与函数y=200(1+5%)x的图象交于A点,则A(x 300),A点
0,
的横坐标x 的值就是函数值y=300时所经过的时间x的值.
0因为80),乙食堂的营业额每月增加的百分率为 x.由题意,可得 m+8a=m(1+
x)8,则5月份甲食堂的营业额y =m+4a,乙食堂的营业额y =m(1+x)4=,因
1 2
为y-y=(m+4a)2- m(m+8a)=16a2>0,所以y >y ,故该年5月份甲食堂的营
1 2
业额较高.
2.某投资公司拟投资开发某种新产品,市场评估能获得10万元~1000万元(包含10万元和1000万元)的投资收益.现公司准备制订一个对科研课题组的奖
励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不
低于1万元,同时不超过投资收益的20%.
(1)设奖励方案的函数模型为f(x),根据题目要求,写出f(x)满足的条件;
(2)下面是公司预设的两个奖励方案的函数模型:
①f(x)=+2;②f(x)=4lg x-2.
试分别分析这两个函数模型是否符合公司的要求.
解 (1)由题意,知公司对奖励方案的基本要求是:
当x∈[10,1000]时,①f(x)是增函数;②f(x)≥1恒成立;③f(x)≤恒成立.
(2)①对于函数模型f(x)=+2:
当x∈[10,1000]时,f(x)是增函数,
且f(x)≥f(10)=≥1,即f(x)≥1恒成立,
而若使函数f(x)=+2≤在[10,1000]上恒成立,
则29x≥300在[10,1000]上恒成立.
又当x=10时,29x=29×10=290<300,
所以f(x)≤在[10,1000]上不恒成立.
故该函数模型不符合公司的要求.
②对于函数模型f(x)=4lg x-2:
当x∈[10,1000]时,f(x)是增函数,
且f(x)≥f(10)=4lg 10-2=2≥1,
所以f(x)≥1在[10,1000]上恒成立.
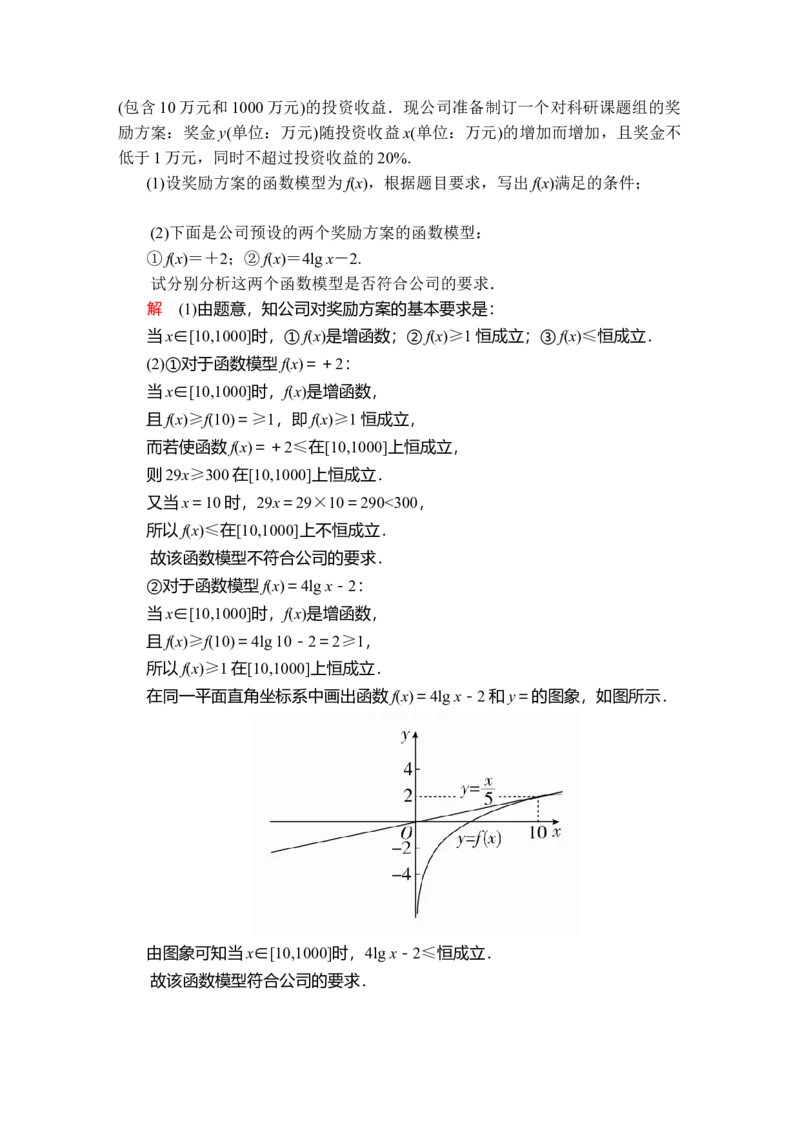
在同一平面直角坐标系中画出函数f(x)=4lg x-2和y=的图象,如图所示.
由图象可知当x∈[10,1000]时,4lg x-2≤恒成立.
故该函数模型符合公司的要求.