文档内容
高一第二学期期末数学试卷
一、选择题(共8小题).
1. 复数 的虚部为( )
A. 2 B. C. 1 D. i
2. 已知向量 , .若 ,则 ( )
A. B. C. D.
3. 在北京消费季活动中,某商场为促销举行购物抽奖活动,规定购物消费每满200元就可以参加一次抽奖
活动,中奖的概率为 .那么以下理解正确的是( )
A. 某顾客抽奖10次,一定能中奖1次
B. 某顾客抽奖10次,可能1次也没中奖
C. 某顾客消费210元,一定不能中奖
D. 某顾客消费1000元,至少能中奖1次
4. 要得到函数 的图象,只要将函数 的图象( )
A. 向右平移 个单位长度 B. 向左平移 个单位长度
C. 向右平移 个单位长度 D. 向左平移 个单位长度
5. 在复平面内,复数 对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6. 设l是直线, , 是两个不同的平面,下列命题正确的是( )
A. 若 , ,则 B. 若 , ,则
C. 若 , ,则 D. 若 , ,则7. 已知A,B,C,D是平面内四个不同的点,则“ ”是“四边形 为平行四边形”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
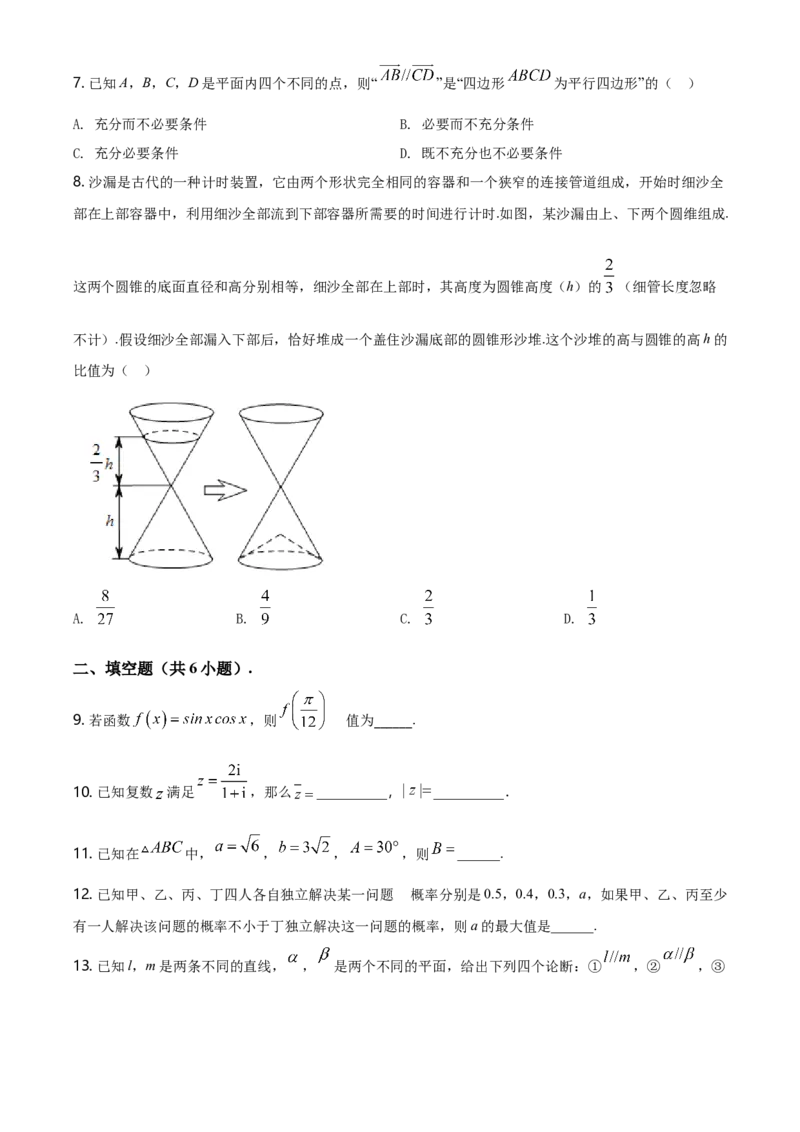
8. 沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全
部在上部容器中,利用细沙全部流到下部容器所需要的时间进行计时.如图,某沙漏由上、下两个圆维组成.
这两个圆锥的底面直径和高分别相等,细沙全部在上部时,其高度为圆锥高度(h)的 (细管长度忽略
不计).假设细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆.这个沙堆的高与圆锥的高h的
比值为( )
A. B. C. D.
二、填空题(共6小题).
9. 若函数 ,则 的值为______.
10. 已知复数 满足 ,那么 __________, __________.
11. 已知在 中, , , ,则 ______.
12. 已知甲、乙、丙、丁四人各自独立解决某一问题 的概率分别是0.5,0.4,0.3,a,如果甲、乙、丙至少
有一人解决该问题的概率不小于丁独立解决这一问题的概率,则a的最大值是______.
13. 已知l,m是两条不同的直线, , 是两个不同的平面,给出下列四个论断:① ,② ,③,④ .以其中的两个论断作为命题的条件, 作为命题的结论,写出一个真命题:______.
14. 在日常生活中,我们会看到如图所示的情境,两个人共提一个行李包.假设行李包所受重力为G,作用
在行李包上的两个拉力分别为 , ,且 , 与 的夹角为 .给出以下结论:
① 越大越费力, 越小越省力;
② 的范围为 ;
③当 时, ;
④当 时, .
其中正确结论的序号是______.
三、解答题共5题,每题10分,共50分.解答应写出文字说明,演算步骤或证明过程.
.
15. 已知函数 ,其 , _____
(1)写出函数 的一个周期(不用说明理由);
(2)当 时,求函数 的最大值和最小值.
从① ,② 这两个条件中任选一个,补充 在上面问题中并作答,
注:如果选择多个条件分别解答.按第一个解答计分.
16. 某医院首批援鄂人员中有2名医生,3名护士和1名管理人员.采用抽签的方式,从这六名援鄂人员中
随机选取两人在总结表彰大会上发言.
(Ⅰ)写出发言人员所有可能的结果构成的样本空间;
(Ⅱ)求选中1名医生和1名护士发言的概率;(Ⅲ)求至少选中1名护士发言的概率.
17. 在正方体 中,E,F分别为 和 的中点.(1)求证: 平面 ;
(2)在棱 上是否存在一点M,使得平面 平面 ?若存在,求出 的值;若不存在,
请说明理由.
18. 在 中, ,D是 的中点, , .
(1)求B;
(2)求 的面积.
19. 对于任意实数a,b,c,d,表达式 称为二阶行列式(determinant),记作 ,
(1)求下列行列式的值:
① ;② ;③ ;
(2)求证:向量 与向量 共线的充要条件是 ;
(3)讨论关于x,y的二元一次方程组 ( )有唯一解的条件,并求出解.(结
果用二阶行列式的记号表示).