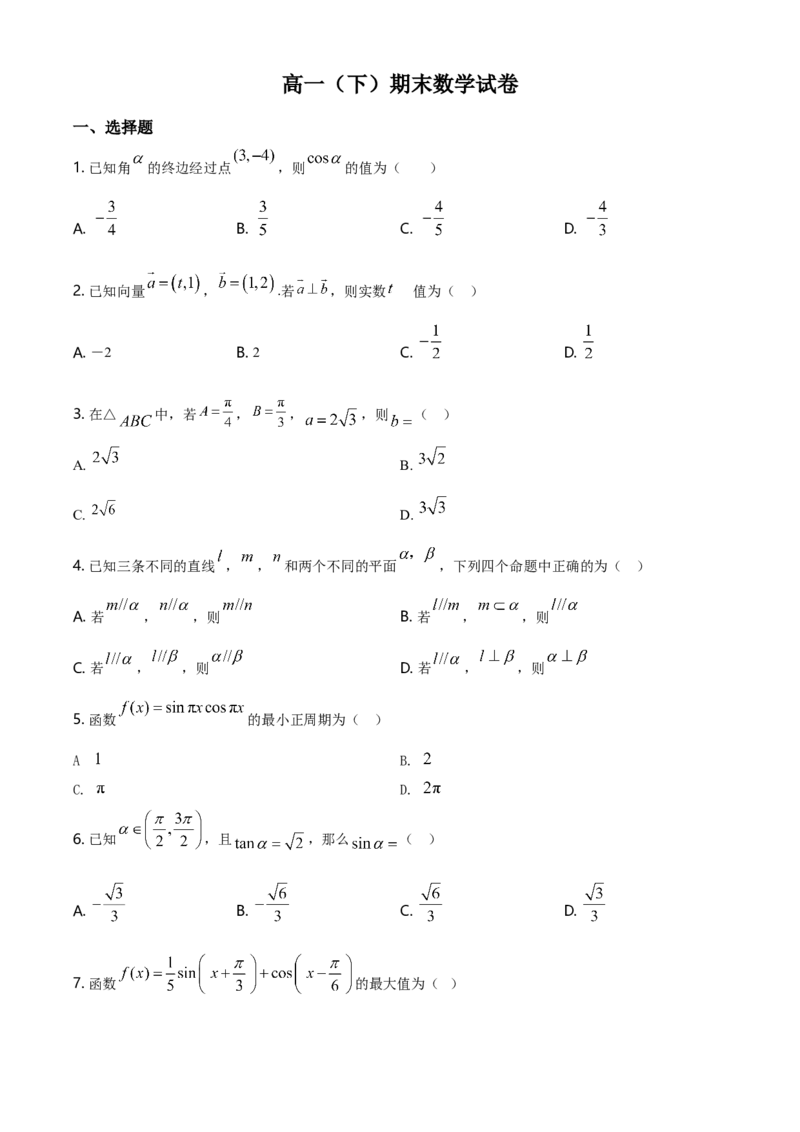文档内容
高一(下)期末数学试卷
一、选择题
1. 已知角 的终边经过点 ,则 的值为( )
A. B. C. D.
2. 已知向量 , .若 ,则实数 的值为( )
A. -2 B. 2 C. D.
3. 在△ 中,若 , , ,则 ( )
A. B.
C. D.
4. 已知三条不同的直线 , , 和两个不同的平面 ,下列四个命题中正确的为( )
A. 若 , ,则 B. 若 , ,则
C. 若 , ,则 D. 若 , ,则
5. 函数 的最小正周期为( )
.
A B.
C. D.
6. 已知 ,且 ,那么 ( )
A. B. C. D.
7. 函数 的最大值为( )A. B. 1 C. D.
8. 已知直线 , ,平面 , , , , ,那么“ ”是“ ” 的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
二、填空题
9. 已知向量 , ,则向量 , 夹角的大小为______.
10. 已知向量 与 的夹角为120°,且 ,那么 的值为______.
11. 在平面直角坐标系中,角 的终边过点 ,则 ___;将射线 ( 为坐标原点)按逆时
针方向旋转 后得到角 的终边,则 ___.
12. 已知 ,则 的值为______.
13. 已知函数 .若 ,则函数 的单调增区间为______.
14. 函数 图象如图,则 的值为______, 的值为______.三、解答题
15. 函数 .
(1)求函数 的单调递增区间和最小正周期;
(2)请用“五点法”画出函数 在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数
值,再画图);0
(3)求函数 在 上的最大值和最小值,并指出相应的 的值.
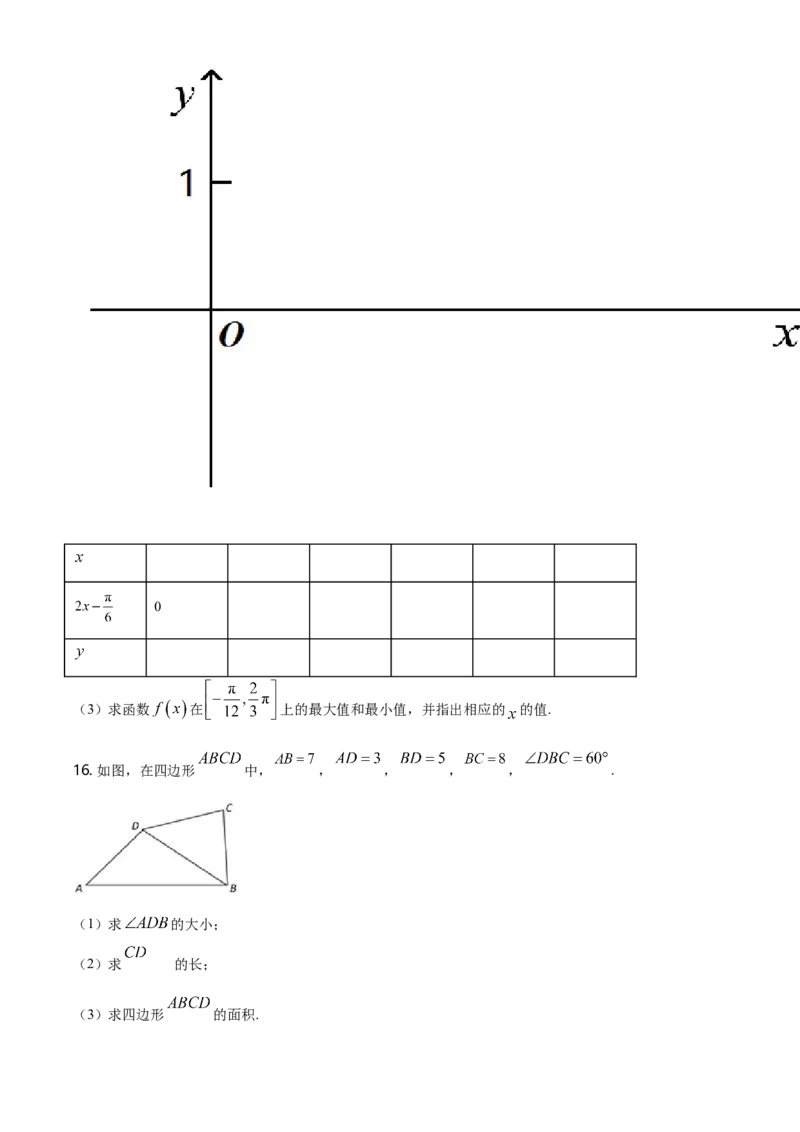
16. 如图,在四边形 中, , , , , .
(1)求 的大小;
(2)求 的长;
(3)求四边形 的面积.17. 如图,在三棱锥 中, , , , 分别是 , ,
的中点,求证:
(1) 平面 ;
(2) 平面 ;
(3)平面 平面 ;
(4)请在图中画出平面 截三棱锥 的截面,判断截面形状并说明你的理由;
(5)若 .求出第(4)问中的截面面积.
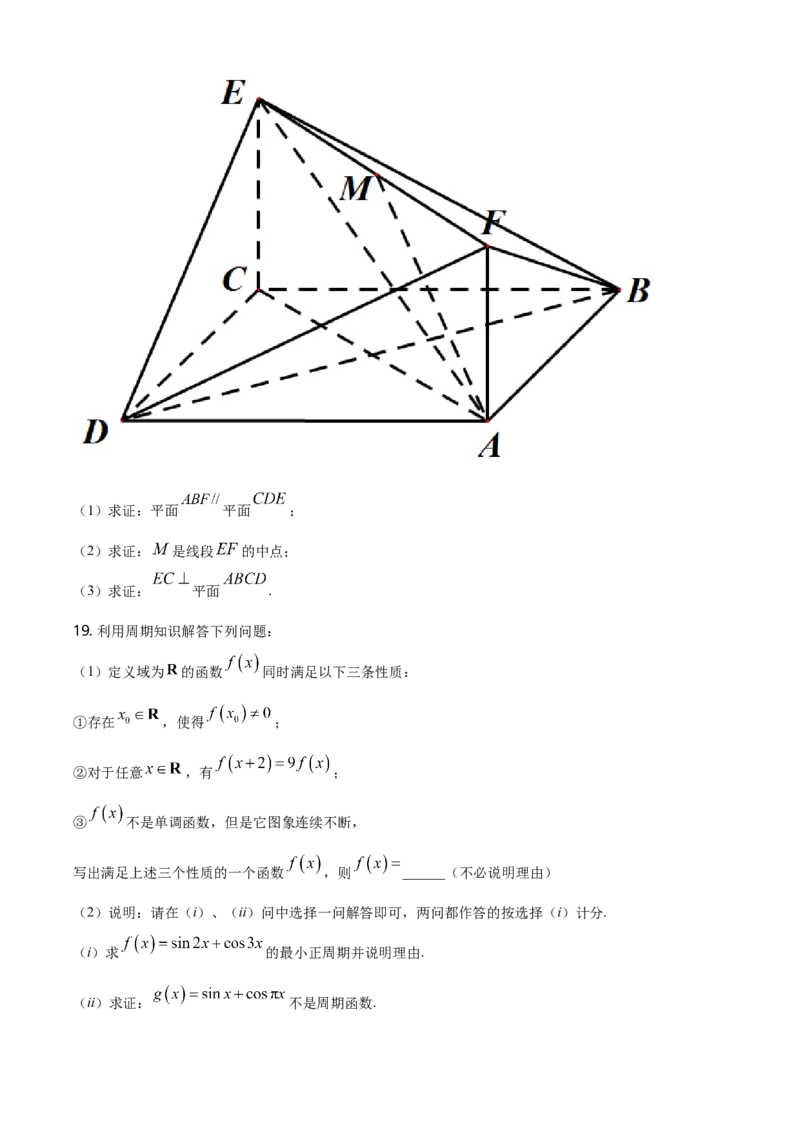
18. 如图,已知正方形 所在平面和平行四边形 所在平面互相垂直,平面 平面
, , 是线段 上的一点且 平面 .(1)求证:平面 平面 ;
(2)求证: 是线段 的中点;
(3)求证: 平面 .
19. 利用周期知识解答下列问题:
(1)定义域为 的函数 同时满足以下三条性质:
①存在 ,使得 ;
②对于任意 ,有 ;
③ 不是单调函数,但是它图象连续不断,
写出满足上述三个性质的一个函数 ,则 ______(不必说明理由)
(2)说明:请在(i)、(ii)问中选择一问解答即可,两问都作答的按选择(i)计分.
(i)求 的最小正周期并说明理由.
(ii)求证: 不是周期函数.