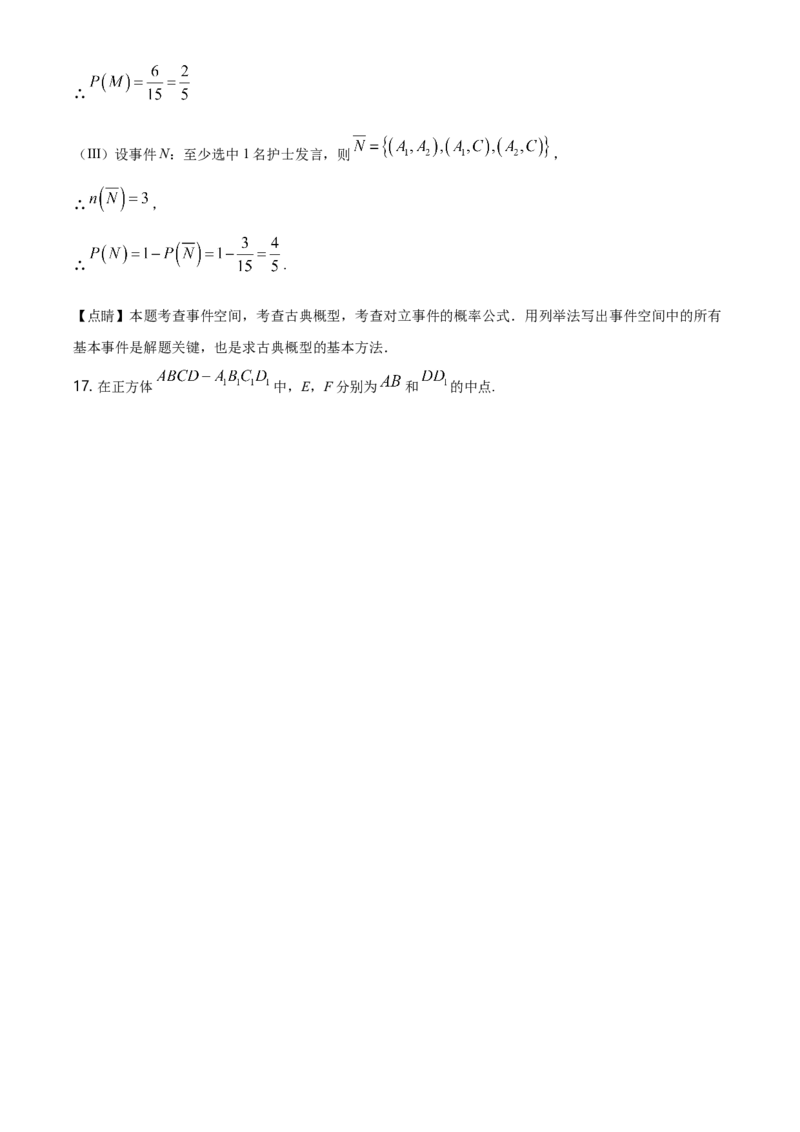文档内容
高一第二学期期末数学试卷
一、选择题(共8小题).
1. 复数 的虚部为( )
A. 2 B. C. 1 D. i
【答案】C
【解析】
【分析】
直接利用复数的基本概念得答案.
【详解】解:复数 的虚部为1.
故选:C.
【点睛】此题考查复数的有关概念,属于基础题
.
2. 已知向量 , 若 ,则 ( )
A. B. C. D.
【答案】A
【解析】
【分析】
根据平面向量的坐标运算,列方程求出x的值.
【详解】解:向量 , ;
若 ,则 ,
即 ,
解得 .
故选:A.
【点睛】此题考查由向量垂直求参数,属于基础题
3. 在北京消费季活动中,某商场为促销举行购物抽奖活动,规定购物消费每满200元就可以参加一次抽奖活动,中奖的概率为 .那么以下理解正确的是( )
A. 某顾客抽奖10次,一定能中奖1次
B. 某顾客抽奖10次,可能1次也没中奖
C. 某顾客消费210元,一定不能中奖
D. 某顾客消费1000元,至少能中奖1次
【答案】B
【解析】
【分析】
根据概率的定义进行判断.
【详解】解:中奖概率 表示每一次抽奖中奖的可能性都是 ,
故不论抽奖多少次,都可能一次也不中奖,
故选:B.
【点睛】此题考查对概率定义的理解,属于基础题
4. 要得到函数 的图象,只要将函数 的图象( )
A. 向右平移 个单位长度 B. 向左平移 个单位长度
C. 向右平移 个单位长度 D. 向左平移 个单位长度
【答案】D
【解析】
【分析】
由题意利用函数 的图象变换规律,得出结论.
【详解】解:只要将函数 的图象向左平移 个单位长度,
即可得到函数 的图象,故选:D.
【点睛】此题考查函数 的图象变换,属于基础题
5. 在复平面内,复数 对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】B
【解析】
【分析】
化简复数,找出对应点得到答案.
【详解】 对应点为 在第二象限
故答案选B
【点睛】本题考查了复数的化简,属于简单题.
6. 设l是直线, , 是两个不同的平面,下列命题正确的是( )
A. 若 , ,则 B. 若 , ,则
C. 若 , ,则 D. 若 , ,则
【答案】D
【解析】
【分析】
利用空间线线、线面、面面的位置关系对选项进行逐一判断,即可得到答案.
【详解】A.若 , ,则 与 可能平行,也可能相交,所以不正确.
B.若 , ,则 与 可能的位置关系有相交、平行或 ,所以不正确.
C.若 , ,则可能 ,所以不正确.
D.若 , ,由线面平行的性质过 的平面与 相交于 ,则 ,又 .
所以 ,所以有 ,所以正确.
故选:D
【点睛】本题考查面面平行、垂直的判断,线面平行和垂直的判断,属于基础题.7. 已知A,B,C,D是平面内四个不同的点,则“ ”是“四边形 为平行四边形”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】B
【解析】
【分析】
根据必要条件、充分条件的定义即可判断.
【详解】解:由 可不一定推出四边形 为平行四边形,
但由四边形 为平行四边形一定可得 ,
故“ ”是“四边形 为平行四边形”的必要而不充分条件,
故选:B.
【点睛】此题考查充分条件和必要条件的判断,考查推理能力,属于基础题
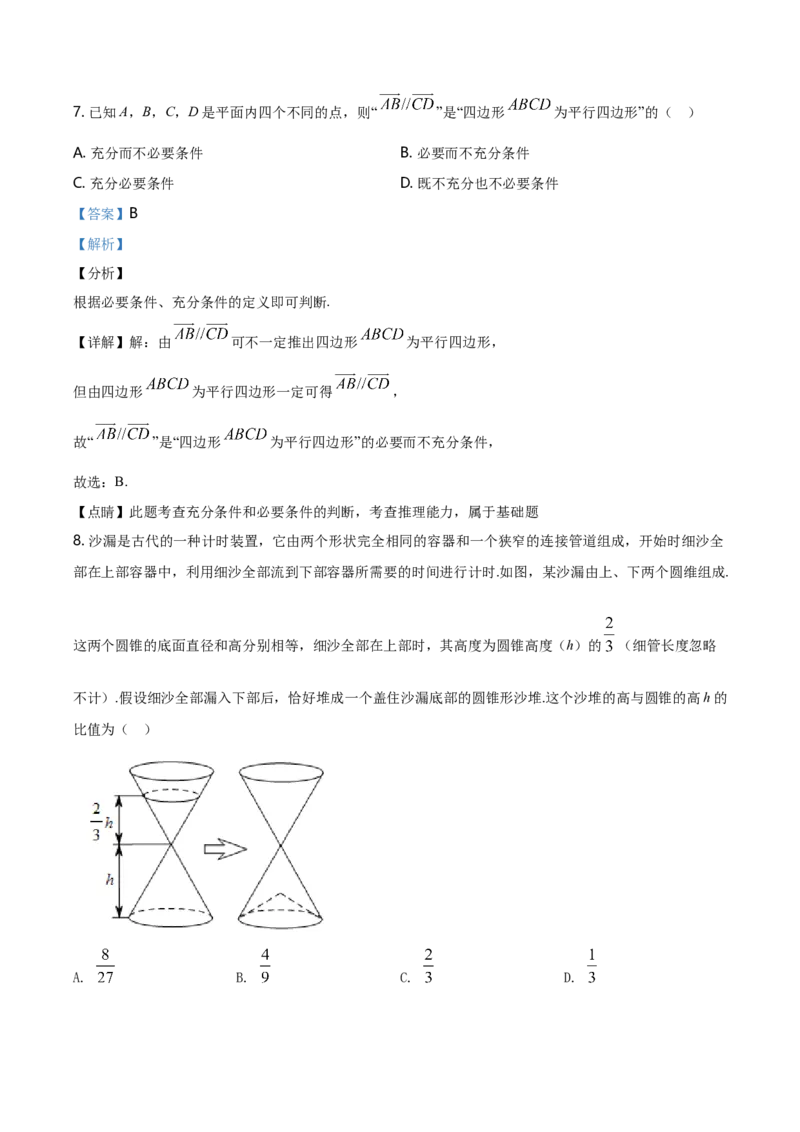
8. 沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全
部在上部容器中,利用细沙全部流到下部容器所需要的时间进行计时.如图,某沙漏由上、下两个圆维组成.
这两个圆锥的底面直径和高分别相等,细沙全部在上部时,其高度为圆锥高度(h)的 (细管长度忽略
不计).假设细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆.这个沙堆的高与圆锥的高h的
比值为( )
A. B. C. D.【答案】A
【解析】
【分析】
细沙全部在上部时,沙漏上部分圆锥中的细沙的高为 ,设圆锥的底面半径为r,则细沙形成的圆锥的底
面半径为 ,求出细沙的体积,再设细沙漏入下部后,圆锥形沙堆的高为 ,求出细沙的体积,由体积
相等求解 ,则答案可求.
【详解】解:细沙全部在上部时,沙漏上部分圆锥中的细沙的高为 ,
设圆锥的底面半径为r,则细沙形成的圆锥的底面半径为 ,
∴细沙的体积为 .
细沙漏入下部后,圆锥形沙堆的底面半径r,设高为 ,
则 ,
得 .
∴ .
故选:A.
【点睛】此题考查圆锥体积公式的应用,属于中档题
二、填空题(共6小题).
9. 若函数 ,则 的值为______.【答案】
【解析】
【分析】
由已知利用二倍角公式可求 ,进而根据特殊角的三角函数值即可求解.
【详解】解:∵ ,
∴ .
故答案为: .
【点睛】此题考查正弦的二倍角公式的应用,属于基础题
10. 已知复数 满足 ,那么 __________, __________.
【答案】 (1). (2).
【解析】
【分析】
利用复数除法运算得到复数 ,进而求出其共轭与模即可.
【详解】复数 ,
故 , .
【点睛】本题考查复数的运算及基本概念,属于基础题.
11. 已知在 中, , , ,则 ______.
【答案】 或 .
【解析】
【分析】由已知利用正弦定理可得 ,结合 ,可得范围 ,即可求解B的值.
【详解】解:∵ , , ,
∴由正弦定理 ,可得 ,
∵ ,可得 ,
∴ ,或 .
故答案为: ,或 .
【点睛】此题考查正弦定理的应用,考查计算能力,属于基础题
12. 已知甲、乙、丙、丁四人各自独立解决某一问题的概率分别是0.5,0.4,0.3,a,如果甲、乙、丙至少
有一人解决该问题的概率不小于丁独立解决这一问题的概率,则a的最大值是______.
【答案】0.79.
【解析】
【分析】
由甲、乙、丙至少有一人解决该问题的概率不小于丁独立解决这一问题的概率,利用对立事件概率计算公
式列出方程,由此能求出a的最大值.
【详解】解:甲、乙、丙、丁四人各自独立解决某一问题的概率分别是0.5,0.4,0.3,a,
∵甲、乙、丙至少有一人解决该问题的概率不小于丁独立解决这一问题的概率,
∴ ,
解得 .
∴a的最大值是0.79.
故答案为:0.79.
【点睛】此题考查对立事件概率的应用,属于基础题
13. 已知l,m是两条不同的直线, , 是两个不同的平面,给出下列四个论断:① ,② ,③
,④ .以其中的两个论断作为命题的条件, 作为命题的结论,写出一个真命题:______.【答案】若 , ,则
【解析】
【分析】
若 , ,则 ,运用线面垂直的性质和判定定理,即可得到结论.
【详解】解:l,m是两条不同的直线, , 是两个不同的平面,
可得若 , ,则 ,
理由:在 内取两条相交直线a,b,
由 可得 . ,
又 ,可得 . ,
而a,b为 内的两条相交直线,可得 .
故答案 为:若 , ,则
【点睛】此题考查线面垂直的判定定理和性质定理的应用,考查推理能力,属于基础题
14. 在日常生活中,我们会看到如图所示的情境,两个人共提一个行李包.假设行李包所受重力为G,作用
在行李包上的两个拉力分别为 , ,且 , 与 的夹角为 .给出以下结论:
① 越大越费力, 越小越省力;
② 的范围为 ;
③当 时, ;
④当 时, .
其中正确结论的序号是______.【答案】①④.
【解析】
【分析】
根据 为定值,求出 ,再对题目中的命题分析、判断正误即可.
【详解】解:对于①,由 为定值,
所以 ,
解得 ;
由题意知 时, 单调递减,所以 单调递增,
即 越大越费力, 越小越省力;①正确.
对于②,由题意知, 的取值范围是 ,所以②错误.
对于③,当 时, ,所以 ,③错误.
对于④,当 时, ,所以 ,④正确.
综上知,正确结论的序号是①④.
故答案为:①④.
【点睛】此题考查平面向量数量积的应用,考查分析问题的能力,属于中档题
三、解答题共5题,每题10分,共50分.解答应写出文字说明,演算步骤或证明过程.
15. 已知函数 ,其 , _____.
(1)写出函数 的一个周期(不用说明理由);
(2)当 时,求函数 的最大值和最小值.从① ,② 这两个条件中任选一个,补充在上面问题中并作答,
注:如果选择多个条件分别解答.按第一个解答计分.
【答案】若选①(1) ;(2)最小值 ,最大值 ;若选②(1) ,(2)最大值 ,
最小值 .
【解析】
【分析】
(1)结合所选选项,然后结合二倍角公式及辅助角公式进行化简,然后结合周期公式可求;
(2)由已知角x的范围,然后结合正弦函数的性质即可求解.
【详解】解:选①,(1)因为 ,
,
故函数的周期 ;
(2)因为 ,所以 ,
当 即 时,函数取得最小值 ,当 即 时,函数取得最大值 ,
选②,(1)
,
,
故函数的一个周期 ,(2)由 可得 ,
时即 时,函数取得最大值 ,
当 时即 时,函数取得最小值 .
【点睛】此题考查二倍角公式及辅助角公式的应用,考查正弦函数性质的应用,考查计算能力,属于中档
题
16. 某医院首批援鄂人员中有2名医生,3名护士和1名管理人员.采用抽签的方式,从这六名援鄂人员中
随机选取两人在总结表彰大会上发言.
(Ⅰ)写出发言人员所有可能的结果构成的样本空间;
(Ⅱ)求选中1名医生和1名护士发言的概率;
(Ⅲ)求至少选中1名护士发言的概率.
【答案】(Ⅰ)样本空间见解析;(Ⅱ) ;(Ⅲ) .
【解析】
【分析】
(Ⅰ)给6名医护人员进行编号,使用列举法得出样本空间;
(Ⅱ)列举出符合条件的基本事件,根据古典概型的概率公式计算概率;
(Ⅲ)列举出对立事件的基本事件,根据对立事件概率公式计算概率.
【详解】解:(Ⅰ)设2名医生记为 , ,3名护士记为 , , ,1名管理人员记为C,
则样本空间为:
.
(Ⅱ)设事件M:选中1名医生和1名护士发言,则
,
∴ ,又 ,.
∴
(Ⅲ)设事件N:至少选中1名护士发言,则 ,
∴ ,
∴ .
【点睛】本题考查事件空间,考查古典概型,考查对立事件的概率公式.用列举法写出事件空间中的所有
基本事件是解题关键,也是求古典概型的基本方法.
17. 在正方体 中,E,F分别为 和 的中点.(1)求证: 平面 ;
(2)在棱 上是否存在一点M,使得平面 平面 ?若存在,求出 的值;若不存在,
请说明理由.
【答案】(1)证明见解析;(2)存在,1.
【解析】
【分析】
(1)取 的中点G,连接 , ,运用中位线定理和平行四边形的判定和性质,结合线面平行的
判定定理,即可得证;
(2)在棱 上假设存在一点M,使得平面 平面 ,取M为 的中点,连接 , ,
,由线面垂直的判定和性质,结合面面垂直的判定定理,可得所求结论.
【详解】解:(1)取 的中点G,连接 , ,因为F为 的中点,
所以 ∥ ,且 ,
在正方体 中,因为E为 的中点,
所以 ∥ ,且 ,所以 ∥ , ,
可得四边形 为平行四边形,
所以 ∥ ,又因为 平面 , 平面 ,
则 ∥平面 ;(2)在棱 上假设存在一点M,使得平面 平面 ,
取M为 的中点,连接 , , ,
因为F为 的中点,所以 ∥ ,因为 ,
可得 ,
因为 平面 , 平面 ,
所以 ,
因为 平面 , 平面 , ,
所以 平面 ,
因为 平面 ,所以平面 平面 ,
故 .【点睛】
此题考查线面平行的判定,考查线面垂直的判定和性质的应用,考查面面垂直的判定,考查推理能力,属
于中档题
18. 在 中, ,D是 的中点, , .
(1)求B;
(2)求 的面积.
【答案】(1) ;(2) .
【解析】
【分析】
(1)直接由已知条件和正弦定理求出B的值.
(2)根据余弦定理求出c的值,再根据面积公式即可求出.
【详解】解:(1)由 及正弦定理,
可得: ,
所以: ,
由于: , ,
因为 ,
解得: ;
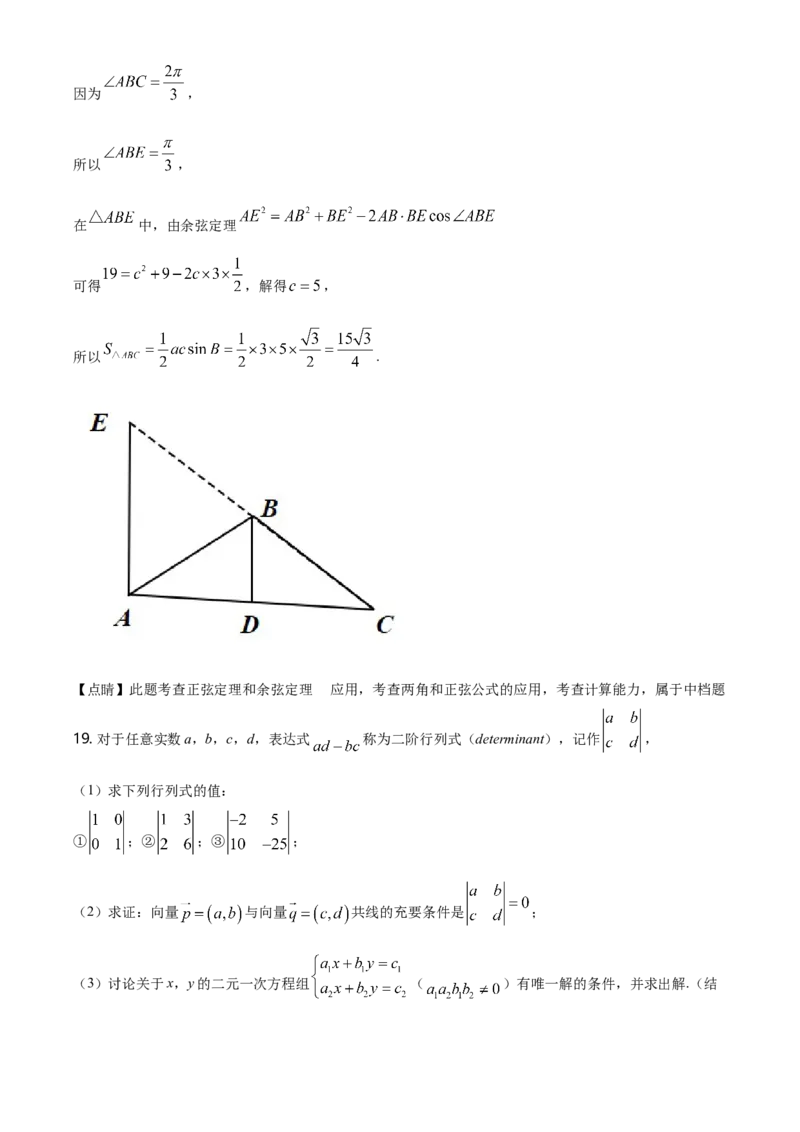
(2)延长线段 到E,使得 ,
因为D是 的中点,
所以 是 的中位线,
所以 ,因为 ,
所以 ,
在 中,由余弦定理
可得 ,解得 ,
所以 .
【点睛】此题考查正弦定理和余弦定理 的应用,考查两角和正弦公式的应用,考查计算能力,属于中档题
19. 对于任意实数a,b,c,d,表达式 称为二阶行列式(determinant),记作 ,
(1)求下列行列式的值:
① ;② ;③ ;
(2)求证:向量 与向量 共线的充要条件是 ;
(3)讨论关于x,y的二元一次方程组 ( )有唯一解的条件,并求出解.(结果用二阶行列式的记号表示).
【答案】(1)1,0,0;(2)证明见解析;(3)当 时,有唯一解, ,
.
【解析】
【分析】
(1)利用行列式的定义可以直接求出行列式的值.
(2)若向量 与向量 共线,由 和 时,分别推导出 ;反之,若
,即 ,当c,d不全为0时,不妨设 ,则 , ,推导出
, ,当 且 时, , 与 共线,由此能证明向量 与
向量 共线的充要条件是 .
(3)求出 , ,由此能求出当 时,关于
x,y的二元一次方程组 ( )有唯一解,并能求出解.
【详解】解:(1)解:①② ;
③ .
(2)证明:若向量 与向量 共线,则:
当 时,有 ,即 ,
当 时,有 ,即 ,
∴必要性得证.
反之,若 ,即 ,
当c,d不全为0时,即 时,
不妨设 ,则 ,∴ ,
∵ ,∴ ,∴ ,∴ 与 共线,
当 且 时, ,∴ 与 共线,
充分性得证.
综上,向量 与向量 共线的充要条件是 .
(3)用 和 分别乘上面两个方程 的两端,然后两个方程相减,消去y得:
,①
同理,消去x,得:
,②∴当 时,即 时,由①②得:
, ,
∴当 时,关于x,y的二元一次方程组 ( )有唯一解,
且 , .
【点睛】此题考查行列式求值,考查向量共线的充要条件的证明,考查二元一次方程有解的条件及解的求
法,考查运算求解能力,属于中档题