文档内容
第二学期高一年级阶段数学检测
必修第四册学分认定考核试卷
说明:本试卷选择题(1-10题)为客观性试题(闭卷30分钟,共40分),填空题与四道大
题(11-19题)为主观性试题(开卷60分钟,共60分(其中含卷面书写分5分)),全卷共
100分;请将答案写在答题纸的相应位置上.
一、选择题:(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.请将正确答案填涂在答题纸上的相应位置)
1. 下面四个说法中,正确说法的个数为( )
(1)如果两个平面有三个公共点,那么这两个平面重合;
(2)两条直线可以确定一个平面;
(3)若 , , ,则 ;
(4)空间中,两两相交的三条直线在同一平面内.
A. 1 B. 2 C. 3 D. 4
2. 设 是一条直线, 、 是两个不同的平面,则下列命题一定正确的是( )
A. 若 , ,则
B. 若 , ,则
.
C 若 , ,则
D. 若 , ,则
3. 在 中, , , ,则 等于( )
A. B. 3 C. D. 21
4. 在 中,根据下列条件解三角形,其中有两个解的是( )
A. , , B. , ,
.
C , , D. , ,5. 若轴截面为正方形的圆柱的侧面积是S,则圆柱的体积为( )
A. B. C. D.
6. 把边长为4的正方形 ,沿对角线 折成空间四边形 ,使得平面 平面 ,则
空间四边形 的对角线 的长为( )
A. 4 B. C. 2 D.
7. 在 中, , , ,则 的面积是( )
A. B. C. D.
8. 已知过球面上 三点的截面和球心的距离等于球半径的一半,且 ,则球面积
是( )
A. B. C. D.
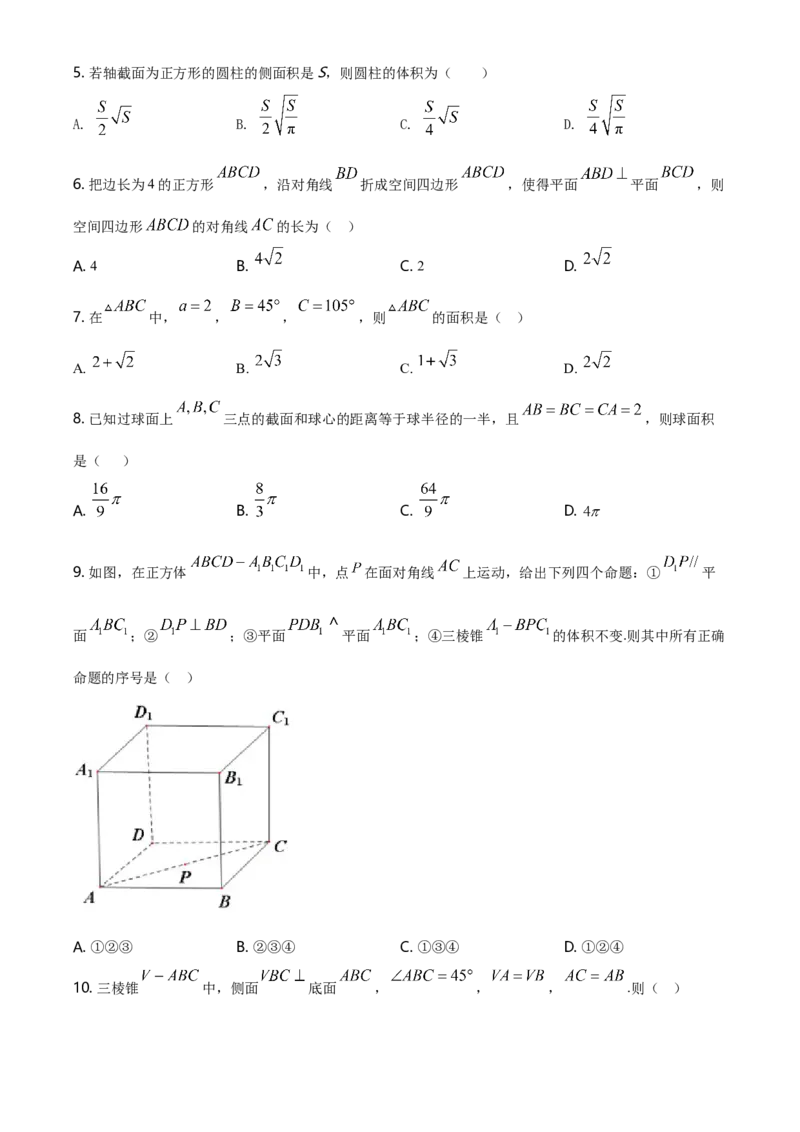
9. 如图,在正方体 中,点 在面对角线 上运动,给出下列四个命题:① 平
面 ;② ;③平面 平面 ;④三棱锥 的体积不变.则其中所有正确
命题的序号是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
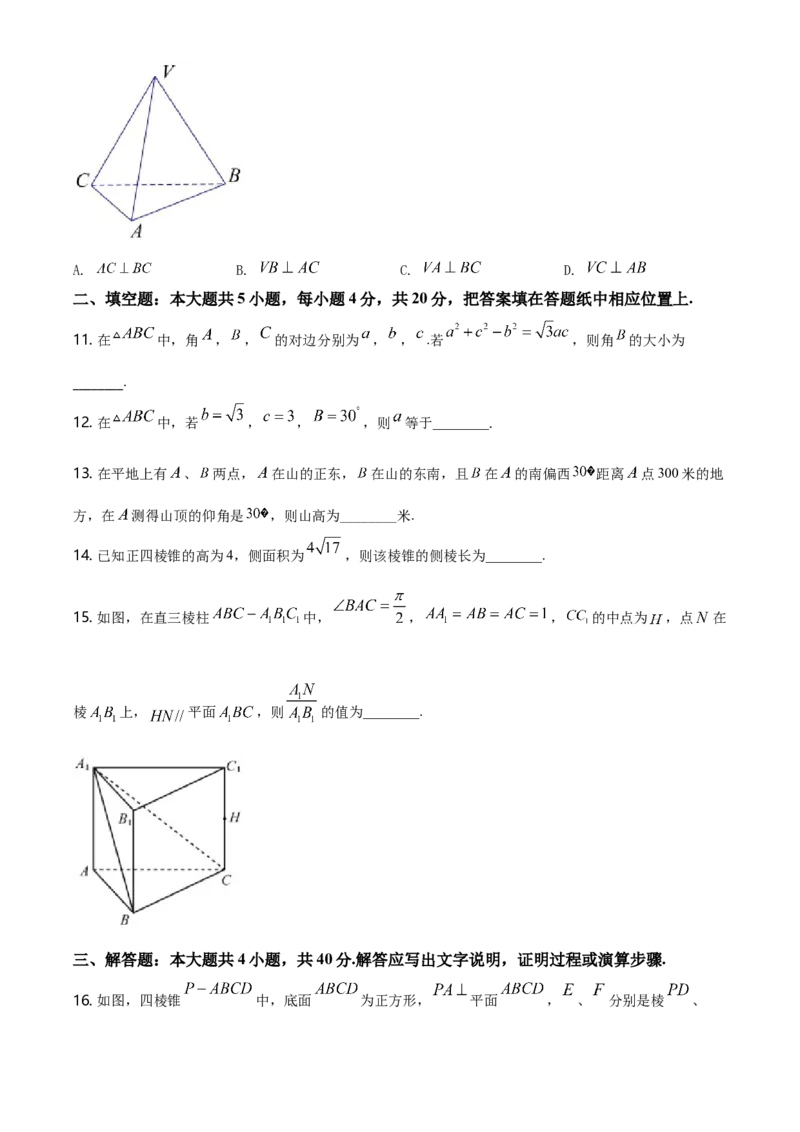
10. 三棱锥 中,侧面 底面 , , , .则( )A. B. C. D.
二、填空题:本大题共5小题,每小题4分,共20分,把答案填在答题纸中相应位置上.
11. 在 中,角 , , 的对边分别为 , , .若 ,则角 的大小为
________.
12. 在 中,若 , , ,则 等于________.
13. 在平地上有 、 两点, 在山的正东, 在山的东南,且 在 的南偏西 距离 点300米的地
方,在 测得山顶的仰角是 ,则山高为________米.
14. 已知正四棱锥的高为4,侧面积为 ,则该棱锥的侧棱长为________.
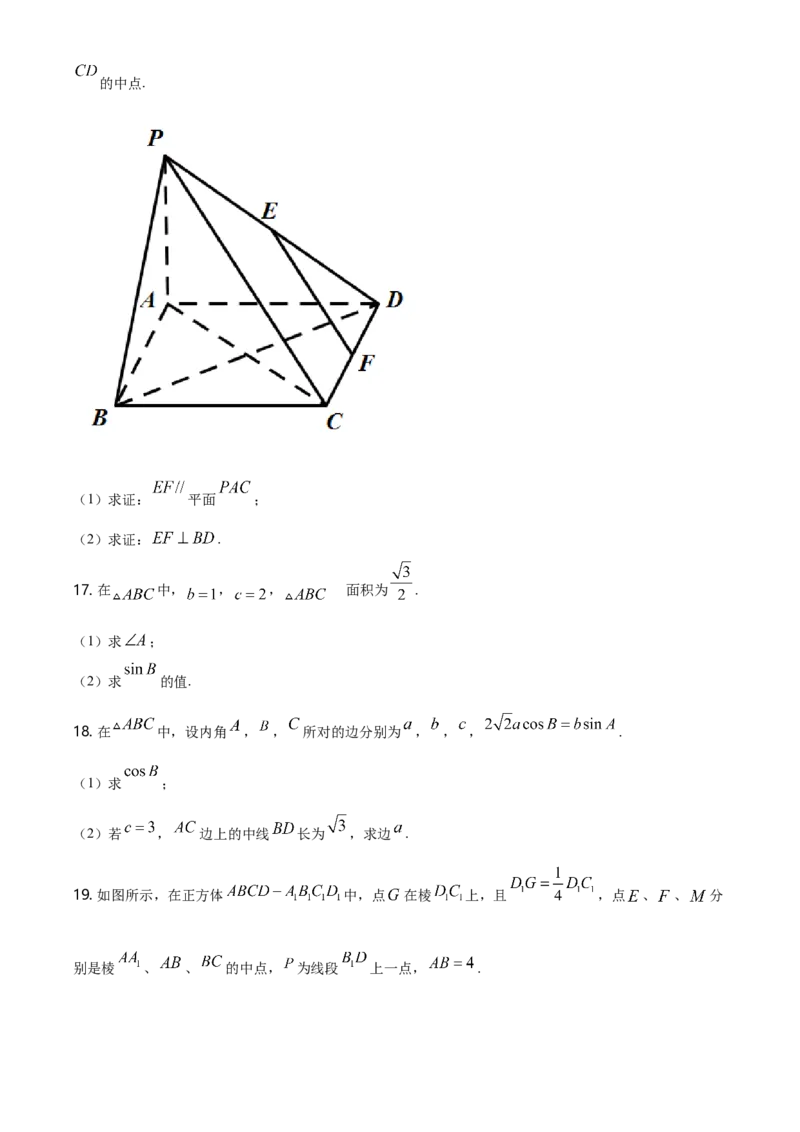
15. 如图,在直三棱柱 中, , , 的中点为 ,点 在
棱 上, 平面 ,则 的值为________.
三、解答题:本大题共4小题,共40分.解答应写出文字说明,证明过程或演算步骤.
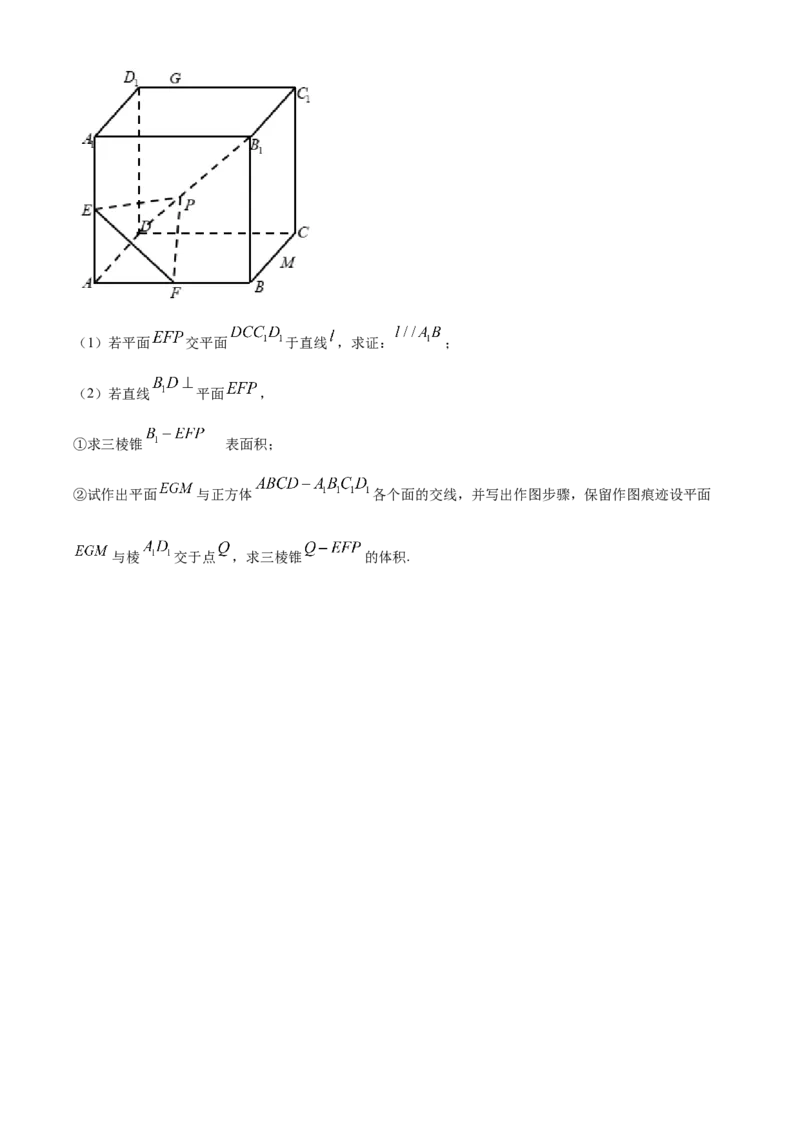
16. 如图,四棱锥 中,底面 为正方形, 平面 , 、 分别是棱 、的中点.
(1)求证: 平面 ;
(2)求证: .
17. 在 中, , , 的面积为 .
(1)求 ;
(2)求 的值.
18. 在 中,设内角 , , 所对的边分别为 , , , .
(1)求 ;
(2)若 , 边上的中线 长为 ,求边 .
19. 如图所示,在正方体 中,点 在棱 上,且 ,点 、 、 分
别是棱 、 、 的中点, 为线段 上一点, .(1)若平面 交平面 于直线 ,求证: ;
(2)若直线 平面 ,
①求三棱锥 的表面积;
②试作出平面 与正方体 各个面的交线,并写出作图步骤,保留作图痕迹设平面
与棱 交于点 ,求三棱锥 的体积.