数学答案（YL）-1_2024年3月_013月合集_2024届湖南省长沙市雅礼中学高三下学期3月综合测试（一）_2024届湖南省长沙市雅礼中学高三下学期3月综合测试（一）数学

雅礼中学 2024 届高三综合自主测试（一）
数学参考答案
一、选择题（本题共8小题，每小题5分，共40分）
1、C【解析】根据题意，数据按从小到大的顺序排列为2，4，m，12，16，17，
3
则极差为17215，故该组数据的中位数是15 9，数据共6个，
5
m12
故中位数为 9，解得m6，因为640%2.4，
2
所以该组数据的第40百分位数是第3个数6，故选：C.
2、A【解析】因为圆心在y轴上，所以可设所求圆的圆心坐标为
0,b
，
则圆的方程为x2 (yb)2 1，又点 1,2 在圆上，所以1 2b 2 1，解得b2，
所以所求圆的方程为x2  y2 2 1．故选：A.
3、D【解析】∵{a }是等差数列，∴a a 2a 10，a 5，
n 3 7 5 5
a a
所以a  5 6 7，∴公差d a a  2，∴a a 4d 3，
6 a 6 5 1 5
5
65
∴S 6(3) 212，故选：D．
6 2
2 1
4、A【解析】若B Ω，AB  1,2  ，则P  AB   ，
4 2
2 1
而P  A   ，P  B 1，所以P  A  P  B P  AB ，
4 2
所以事件A,B相互独立，反过来，当B  1,3 ，AB  1 ，
1 1
此时P  AB  ，P  A  P  B  ，满足P  A  P  B P  AB ，
4 2
事件A,B相互独立，所以不一定B ，
所以甲是乙的充分不必要条件.故选：A
5、D【解析】依题意，由I(x) 1 2 I 0 ， I(x) I 0 e  (x 2 2)2 ，得I 0 e  (x 2 2)2  1 2 I 0 ，
即
(x2)2
，
e 2 2
则有(x2)2 2ln2，解得x 2 2ln2 ，x 2 2ln2 ，
1 2
数学（YL）答案 （第 1 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#}所以3dB带宽为x x  2 2ln2 .故选：D
2 1
x2 y2
6、A【解析】因为函数y f(x)的图象恰为椭圆C:  1(a b0)x轴上方的部分，
a2 b2
所以y f(x)b 1
x2
(axa)，因为 f(st)， f(s)， f(st)成等比数列，
a2
所以有 f2(s) f(st)f(st) ，且有asa,asta,asta成立，
即asa,ata成立，
s2 (st)2 (st)2
由 f2(s) f(st) f(st)(b 1 )2 b 1 b 1 ，
a2 a2 a2
化简得：t4 2a2t22s2t2 t2(t22a22s2)0t2 0，或t22a22s2 0，
当t2 0时，即t 0，因为asa，
所以平面上点（s，t）的轨迹是线段（不包含端点）；
当t22a22s2 0时，即t2 2a22s2，
因为at a，所以t2 a2，而2a22s2 a2，
所以t2 2a2 2s2不成立，故选：A
    
 1   1tan2  2tan2 
7、A【解析】 tan  tan 2     1tantan 2   6 tan  2   1 1tan2  2    6.
 2  2  2 
    
2cos1tan2 2tan2

2cos1tan2

 2 2 6，  2 6，
sin
 1tan2


sin
1tan2


 2   2 
2cos 1 1 1
 6，sin ，sincoscossin ，
sin cos
3 3
又因为tantan      3，所以sincos3cossin，
2 
1 1
则cossin ,sincos ，所以
6 2
2 4 1
sinsincoscossin cos2212sin212  .
3 9 9
1 79
cos442cos22212 1 .故选：A
81 81
 2014π2 
8、C【解析】2cos2xcos2xcos cos4x12cos22x2 ，
 
  x 
2014π2 
令a cos2x,bcos ，则2a  ab 2a22，即ab1，
 x 
所以a 1,b1或a1,b1，
数学（YL）答案 （第 2 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#}2014π2 
当a1,b1时，即cos2x1,cos 1，
 x 
1007π
所以xkπ,kZ,x ,k Z ，
k 1
1
因为1007=11953，所以x=π,19π,53π,1007π，
2014π2 
当a1,b1时，即cos2x1,cos 1，
 x 
 2k1  π 2014π2 4028π
x ,kZ,x  ,k Z
则 2  2k 1  π 2k 1 1 ，
1 1
2
4028
因为2k1是奇数，所以 也是奇数，不成立；
2k 1
1
所以方程所有正根的和为：π+19π+53π+1007π=1080π,故选：C
二、选择题（本题共3小题，每小题6分，共18分）
9、ACD【解析】b2 40，∴ x
b 4b2i，
2
b 4b2 b 4b2
不妨设z   i，z   i，z  z ，A正确；
1 2 2 2 2 2 1 2
b 4b2
z  z  ( )2( )2 1 ，C正确；
1 2 2 2
z z2 b2 2 b 4b2 z
z z 1，∴ 1  1  z2   i，b0时， 1 R，B错；
1 2 z z z 1 2 2 z
2 1 2 2
1 3 1 3 1 3
b1时，z   i，z   i，计算得z2   i z  z ，
1 2 2 2 2 2 1 2 2 2 1
z2  z  z ，z3  z z 1，同理z3 1，D正确．
2 1 2 1 1 2 2
故选：ACD．
10、BD【解析】对于A：连接BD，且ACBD O，如图所示，当M 在PC中点时，
数学（YL）答案 （第 3 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#}因为点O为AC的中点，所以OM//PA，因为PA平面ABCD，
所以OM 平面ABCD，又因为AC平面ABCD，所以OM  AC ，
因为ABCD为正方形，所以ACBD.
又因为BDOM O，且BD，OM 平面BDM ，所以AC 平面BDM ，
因为BM平面BDM ，所以AC BM ，所以A错误；
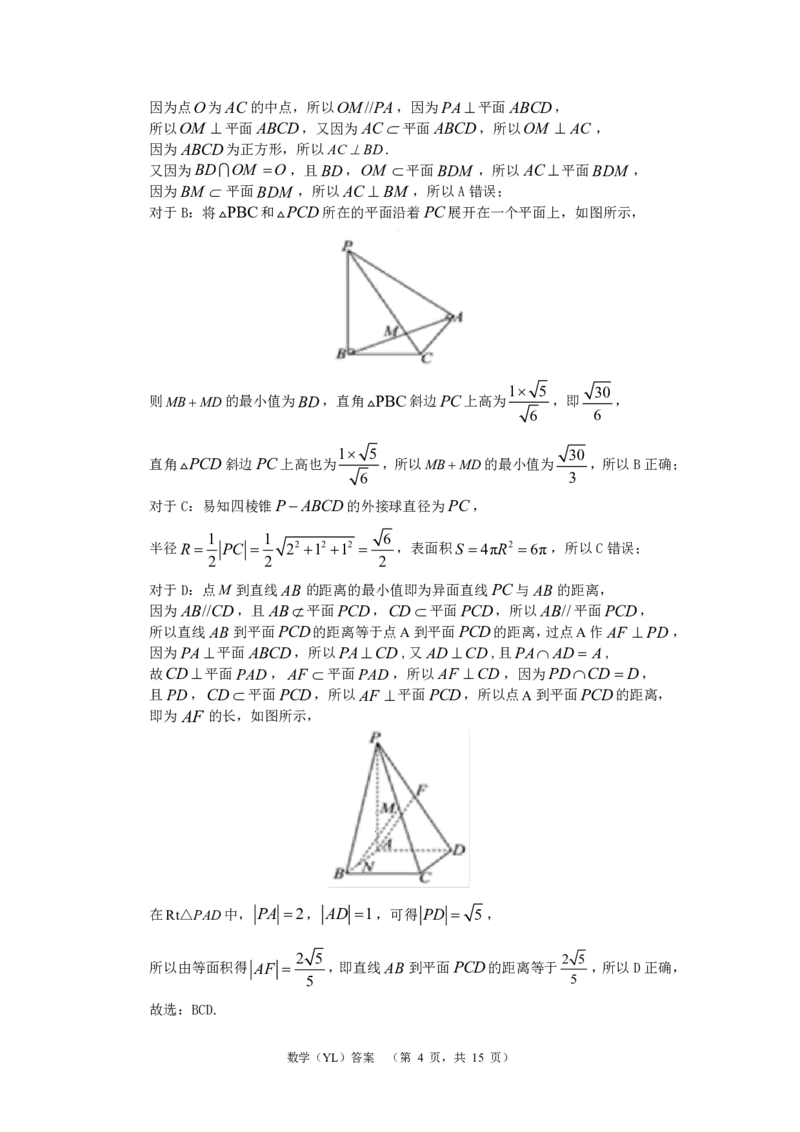
对于B：将PBC和PCD所在的平面沿着PC展开在一个平面上，如图所示，
1 5 30
则MBMD的最小值为BD，直角PBC斜边PC上高为 ，即 ，
6 6
1 5 30
直角PCD斜边PC上高也为 ，所以MBMD的最小值为 ，所以B正确；
6 3
对于C：易知四棱锥PABCD的外接球直径为PC，
1 1 6
半径R  PC  22 12 12  ，表面积S 4πR2 6π，所以C错误；
2 2 2
对于D：点M 到直线AB 的距离的最小值即为异面直线PC与AB 的距离，
因为AB//CD，且AB平面PCD，CD平面PCD，所以AB//平面PCD，
所以直线AB 到平面PCD的距离等于点A到平面PCD的距离，过点A作AF PD ，
因为PA平面ABCD，所以PACD,又AD CD,且PAAD  A,
故CD平面PAD，AF 平面PAD，所以AF CD，因为PDCD D，
且PD，CD平面PCD，所以AF 平面PCD，所以点A到平面PCD的距离，
即为 AF 的长，如图所示，
在Rt△PAD中， PA 2， AD 1，可得 PD  5，
2 5 2 5
所以由等面积得 AF  ，即直线AB到平面PCD的距离等于 ，所以D正确，
5 5
故选：BCD.
数学（YL）答案 （第 4 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#}1
11、ABC【解析】 f(0) , f(x y) f(x)f(a y) f(y)f(ax)
2
1 1 1
对A：对原式令x  y 0，则  f  a  f  a  f  a ，
2 2 2
1
即 f  a  ，故A正确；
2
对B： 对原式令 y 0，
1 1
则 f  x  f  x  f  a  f  0  f  ax  f  x  f  ax ，
2 2
故 f  x  f  ax  ，
对原式令x  y，
则 f

2x

f

x

f

y

f

y

f

x
2f 
x

f

y
2f 2
x
0，故
f

x

非负；
1 1
对原式令 y  ax，则 f  a  f 2 x  f 2 ax 2f 2 x  ，解得 f  x  ，
2 2
1
又 f  x  非负，故可得 f  x  ，故B正确；
2
对C：由B分析可得： f  x y 2f  x  f  y  ，故C正确；
 
对D：由B分析可得：满足条件的 f x 只有一个，故D错误.
故选：ABC.
三、填空题（本题共3小题，每小题5分，共15分）
12、40
【解析】 x2y 6的通项公式为T Crx6r2y r Cr 2 r x6ryr，
r1 6 6
令r 2得，T C22 2 x4y2 60x4y2，此时60x4y22120x4y2，
3 6
x
令r 3得，T C32 3 x3y3 160x3y3，此时160x3y3 160x4y2，
4 6 y
故x4y2的系数为12016040
故答案为：40
2 7
13、①. 7 ②.
7
【解析】如图，将圆锥侧面沿母线PA剪开并展开成扇形，
4π 2π
易知该扇形半径为2，弧长为 ，故圆心角∠APB＝ ，
3 3
最短路线即为扇形中的直线段AB，由余弦定理易知
AB＝ PA2 PB2 2PAPBcosAPB ＝ 7 ，
数学（YL）答案 （第 5 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#}PB2  AB2 PA2 2 7
cos∠PBA＝ ＝ ；
2PBBA 7
过P作AB的垂线，垂足为M，
当蚂蚁从A点爬行到M点的过程中，它与点P的距离越来越小，故AM为上坡路段，
当蚂蚁从M点爬行到B点的过程中，它与点P的距离越来越大，故MB为下坡路段，
2 7
下坡路段长MB＝PB･cos∠PBA＝ ．
7
2 7
故答案为： 7 ， .
7
14、①. 18 ②. 25270
【解析】第一个空，设某个数除以a余数为b，则称该数模a余b(a，b均为整数，且
ba)，
为了让尽可能多的相邻两数之和被3整除，则要尽量多地出现相邻两数一个模3余1，
一个模3余2这样的组合，这样它们之和才会被3整除.
而a 1，a 40均为模3余1，则不可能有19组上述组别，最多出现18组上述组
1 20
别，例如严格递增数列1,2,4,5,7,8,10,11,13,14,16,17,19,20,22,23,25,26,28,40，满足
题意，所以 f 的最大值为18.
第二个空，因为1-40这40个数中，共有27个数符合模3余1或模3余2，则要从这
27个数中选出满足要求的20个数.
第一步，在a 到a 这20个数中删去一个数（后面再加回来），使得剩下的19个数满
1 20
足任意两个相邻数一个模3余1，一个模3余2，这样就形成了18组，即使得 f 的最大值
为18.
第二步，将这27个数从小到大排列，需要删去8个数得到目标19个数的数列.它们中
任意相邻两数一个模3余1，一个模3余2，因此，需要删去的8个数应该为4组相邻的数.
第三步，利用捆绑思想，从27个数中删去4组相邻的数等价于从23个数中删去4个数.
有三种情况：
①两端均删去，这种情况不满足要求.因为若两端均删去，那么1和40必定被删去，在
下一步加出来时也最多加回1或40中的一个，而1和40必定在数列中，因此不满足.
②两端均不删去，从中间21个数中选4个数删去，有C4 种，再从删去的8个数中拿
21
一个加回原来的19个数中，由C1种，共有C4 C1种.
8 21 8
数学（YL）答案 （第 6 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#}③两端中有一个被删去，其余3个数从中间21个数里选，有2C3 种，此时加回来的数
21
必定是删去的两端之一中的1或40，有1种选法，共2C3 种.
21
第四步，删去的四组相邻数中有一组中有一个数被加回来，即未被删去，被删去的是这
一组中的另一个数，而对于删去的数，假设为A，它旁边两个数分别为B,C ，即排列为
B,A,C，在第三步捆绑时，可能捆绑的组合为BA，然后删去，再补回B；或者为AC，
然后删去，再补回C，这两种删去方式结果相同.
1 
综上，共有 C4 C1 2C3 25270种.
2 21 8 21
故答案为：18；25270
四、解答题（本题共6小题，共70分）
15、（1）因为抛物线C的焦点为F0,1，
所以 p2，即C的方程为：x2 4y，如下图所示：
设点Ax,y ,Bx ,y ，
1 1 2 2
由题意可知直线l的斜率一定存在，设l:ykx1，
x2 4y
联立

得x24kx40，
ykx1
所以x x 4k,xx 4.
1 2 1 2
1 1
由x2 4y，得 y x2,y x ，
4 2
x x x2
所以 l :yy  1xx ，即 y 1 x 1 .
1 1 2 1 2 4
令 y0 ，得 x x 1 ，即 D   x 1,0   ，
2  2 
x x2 x 
同理 l :y 2 x 2 ，且 E 2 ,0 ，
2 2 4  2 
1 1
所以 DE  x x  x x 24xx 2 k21 .
2 1 2 2 1 2 1 2
数学（YL）答案 （第 7 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#} x x2
由  

y 2 1 x 4 1 ，得 

x2k ，即M2k,1.
 x x2 y1
y 2 x 2

2 4
所以 MF  4k24 2 k21.
故 DE  MF .
（2）设点Px ,y ，结合（1）知 l :yy  x 1xx ，即l :2xx4yx2 0
0 0 1 1 2 1 1 1 1
因为x2 4y ,x2 4y ，
1 1 0 0
2xx 4y x2 2xx x2x2 x x 2
所以 d  1 0 0 1  1 0 0 1  1 0 .
1 4x216 4x216 2 x24
1 1 1
x x 2
同理可得 d  2 0 ，
2 2 x24
2
所以 dd  x 1 x 0 2  x 2 x 0 2    x 1 x 2 x 0 x 1 x 2 x 0 2  2   44kx 0 x 0 22 .
1 2 2 x24 2 x24 4 x2x 2 4  x2 x 2 16 32 k21
1 2 1 2 1 2
x2
kx  0 1
kx y 1 0 4 4kx x24
又 d  0 0   0 0 ，
k21 k21 4 k21
所以d
1
d
2 
 44kx
0
x
0
22

16  k2 1 

k21

1.
d2 32 k21  4kx x2 4 2 2 2
0 0
当且仅当k 0时，等号成立；
即直线l斜率为0时， d 1 d 2 取最小值1 .
d2
2
π
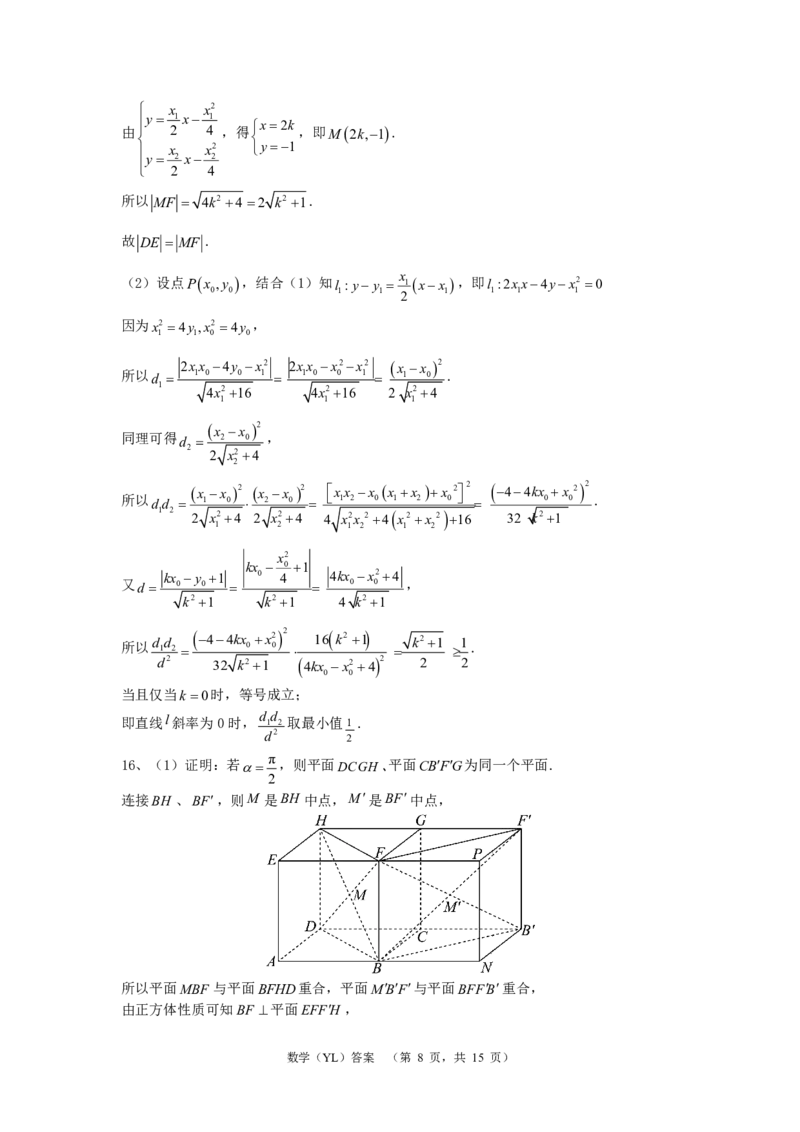
16、（1）证明：若 ，则平面DCGH ､平面CBFG为同一个平面.
2
连接BH 、BF，则M 是BH 中点，M是BF中点，
所以平面MBF 与平面BFHD重合，平面MBF与平面BFFB重合，
由正方体性质可知BF 平面EFFH ，
数学（YL）答案 （第 8 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#}因为HF、FF平面EFFH，所以，BF HF，BF FF，
HFF为二面角HBFF的平面角，
π π π
因为HGFG，HGF  ，则HFG ，同理可得FFG ，
2 4 4
π
所以HFF ，所以，平面MBF 平面MBF
2
（2）解：假设存在，使得直线MF平面MBC，
  
以C为原点，分别以CB、DC、CG的方向分别为x、y、z轴的正方向建立如下图所示的
空间直角坐标系，
 
则C0,0,0、B2,0,0、M1,1,1，故CB2,0,0、CM 1,1,1，
 
设平面MBC的法向量为m  x,y,z，则  

m

C

M

xyz 0 ，
mCB2x0

取y1，得m0,1,1是平面MBC的一个法向量，
取
CG
的中点P，BF的中点Q，连接
PQ
、PM，则P0,0,1，
因为 MG  MC  121212  3，则PM CG，同理可知，PMCG，
因为BQ//CP，BQCP，BQBC，则四边形BCPQ为矩形，所以，PQCG，
于是MPM是二面角M CGM的平面角，
MPQ是二面角M CGQ的平面角，
QPM是二面角QCGM的平面角.于是MPM，
 
因为  P  M  1,1,0，  P  Q  2,0,0， cosMPQ  P  M  P  Q   2  2，
PM  PQ 22 2
π π
因为0MPQπ，则MPQ ，所以QPM ，
4 4
因为PM CG，PMCG，PM PMP，PM 、PM平面MPM，
所以，CG平面MPM，且 MP  MP  2，
故 M   2cos   π , 2sin   π  ,1   ，同理F2cos,2sin,2，
  4  4 
数学（YL）答案 （第 9 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#}   π  π  
所以 MF2cos 2cos ,2sin 2sin ,1 ，
  4  4 
 π π π
因为 2cos 2cos 2cos 2coscos  2sinsin cossin ，
 4 4 4
 π π π
2sin 2sin 2sin 2sincos  2cossin cossin ，
 4 4 4

所以MFcossin,cossin,1，
  
若直线MF平面MBC，m是平面MBC的一个法向量，则MF//m，
cossin0
 
即存在R，使得MFm，则
cossin
，

1
因为02 cossin2cossin2 2，可得2 2，
cossin0
故方程组 无解，
cossin

1
所以不存在0,π，使得直线MF平面MBC.
17、（1）∵ f(x)lnxax2bx
1
∴ f(x) 2axb .
x
∵函数 f(x)lnxax2bx 在x1处取得极值，
∴ f(1)12ab0
1 2x23x1
∴当a1时，b3，则 f(x) 2x3
x x
f(x)、
f(x)
随x的变化情况如下表：
x (0, 1 ) 1 ( 1 ,1) 1 (1,)
2 2 2
f(x) ＋ 0 － 0 ＋
f(x) 极大值 极小值
1 1
∴
f(x)
的单调递增区间为
(0, )
和(1,)，单调递减区间为
( ,1)
2 2
∴
f(x)
的极大值点为1 ，
f(x)
的极小值点为1.
2
数学（YL）答案 （第 10 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#}1 2ax2(2a1)x1 (2ax 1)(x 1)
（2）∵ f(x) 2axb  (x0)
x x x
1
令 f(x)0得，x 1， x 
1 2 2a
∵
f(x)
在x1处取得极值
1
∴ x   x 1
2 2a 1
1
法一：当 0 时， f(x) 在(0,1)上单调递增，在(1,e]上单调递减，
2a
∴
f(x)
在区间(0,e]上的最大值为 f(1)，则 f(1)1，即a12a1
∴a2
1
法二：当a0时， x  0
2 2a
1 1 1
①当 1 时， f(x) 在 (0, ) 上单调递增， ( ,1) 上单调递减，(1,e]上单调递增，
2a 2a 2a
1
∴ f(x) 的最大值1可能在 x 或xe处取得，
2a
1 1 1 1 1 1
而 f( )ln a( )2(2a1) ln  10
2a 2a 2a 2a 2a 4a
∴ f(e)lneae2(2a1)e1
1
∴a
e2
1 1 1
②当 1 e 时， f(x) 在区间(0,1)上单调递增， (1, ) 上单调递减， ( ,e] 上单调递增
2a 2a 2a
∴ f(x) 的最大值1可能在x1或xe处取得，而 f(1)ln1a(2a1)0
1 1
∴ f(e)lneae2(2a1)e1，即a ，与 1 x  e
e2 2 2a
1
③当 e 时， f(x) 在区间(0,1)上单调递增，在(1,e]上单调递减，
2a
∴
f(x)
的最大值1可能在x1处取得，而 f(1)ln1a(2a1)0，矛盾．
1
综上所述，a 或a2.
e2
18、（1）

f(x)4x3，
 f(x)在点x ,y 处的切线方程为：yy 4x3xx 
n n n n n
3
令 y0 ，得 x  x ，
n1 4 n
3
所以x 是首项为1，公比为 的等比数列，
n
4
n1
故 x 


3

n 4
数学（YL）答案 （第 11 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#}n1
3
（2）令 b nx n 
n n 4
法一：错位相减法
0 1 2 n1
3 3 3 3
S 1  2  3  ...n  ，
n 4 4 4 4
3 3 1 3 2 3 3 3 n
S 1  2  3  ... n  ，
4 n 4 4 4 4
1 2 n1 n
两式相减得：1
S 1


3
 


3
 


3
 n


3

4 n 4 4 4 4
n
化简得： S 16(164n)


3

n 4
n n
故 16(164n)


3
 16


5
 ，
4 6
n
化简得(164n) 

9 

10
n
令 d (164n)   9   ，
n 10
则 d d    2n10    9   n ，
n1 n  5 10
当n5时，d d 0，即d d d d d d ，
n1 n 6 5 4 3 2 1
当n6时，d d 0，即d d d ...，
n1 n 6 7 8
5
所以d  d d 36   9    21.26
n max 5 6 10
从而整数 22；
min
法二：裂项相消法
n
由 b nx  4 n   3  ，
n n 3 4
n
设 c n (knm)    3 4    且b n c n1 c n ，
数学（YL）答案 （第 12 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#}则4 n   3  n    kn  3k m    3  n ，
3 4  4 4 4
 k 4
   16
于是   4 3 ，得k  ，
  3
3km
0  m16
 4
n
 16 3
即 c  n16 
n  3 4
所以S
n
b
1
b
2
b
n


c
2
c
1
c
3
c
2
c
n1
c
n


n
3
c c 16(164n) 
n1 1 4
n n n
故 16(164n)   3  16   5  ，化简得(164n)   9  
4 6 10
n
令 d (164n)   9   ，
n 10
则d n1  459n 1 时，n5，
d 4010n
n
d
当n5时， n1 1 ，即d d d d d d ，
6 5 4 3 2 1
d
n
当n6时， 0 d n1 1 ，即d d d ...，
6 7 8
d
n
5
所以d  d d 36   9   21.26
n max 5 6 10
从而整数 22
min
4
19、（1）ysin x不是“M 函数”，理由如下：
3
 3π 4 3π  4  4
f x sin x sin x2π sin x f x ，
 2  3 2  3  3
f   π x  sin 4  π x  sin   π  4 x   ， f   π x  sin 4  π x  sin   π  4 x   ，
4  34  3 3  4  3 4   3 3 
则 f   π x   f   π x   ，
4  4 
4
故ysin x不是“M 函数”；
3
（2）函数 f x满足 f x f

x
3π
 ，故 f x的周期为 T 
3π
，
 2  2
数学（YL）答案 （第 13 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#}π  π 
因为 f  x f  x ，
4  4 
π 
所以 f x f  x ，
2 
当 x   3 kπ π , 3 kππ   时， f x f  x 3 kπ   sin  x 3 kπ   ，kZ，
2 4 2   2   2 
3 π 3 π π  3   π  3   3 
当 x  kπ , kπ  时， f x f  x kπ  sin x k π  cosx k π ，
2 2 2 4 2  2  2  2   2 
kZ，
  3  3 π 3 π
cosx kπ,x  kπ , kπ  ,k Z
综上： f x    2  2 2 2 4 ，
  3  3 π 3 
 
sin

x
2
kπ

,x
  2
kπ
4
,
2
kπ π
 
,k Z
 3  3 π 3 
f xsinx kπ,x

kπ , kπ π

,k Z 中，
 2  2 4 2 
当k 0时， x   π ,π   ， fxsinx ，此时单调递增区间为   π , π  ，
4  4 2
f xcos  x 3 kπ   ， x   3 kπ π , 3 kπ π ,kZ 中，
 2  2 2 2 4
当k1时， x   π, 7π  ， f xcos  x 3 π   ，
 4   2 
3  1 π
则 x π   π,  ，
2  2 4
当 x 3 π    1 π,0   ，即 x   π, 3 π   时，函数单调递增，
2  2   2 
经检验，其他范围不是单调递增区间，
所以在
 3π
上的单调递增区间为
π π
，
 3π
；
 0,   ,   π, 
 2  4 2  2 
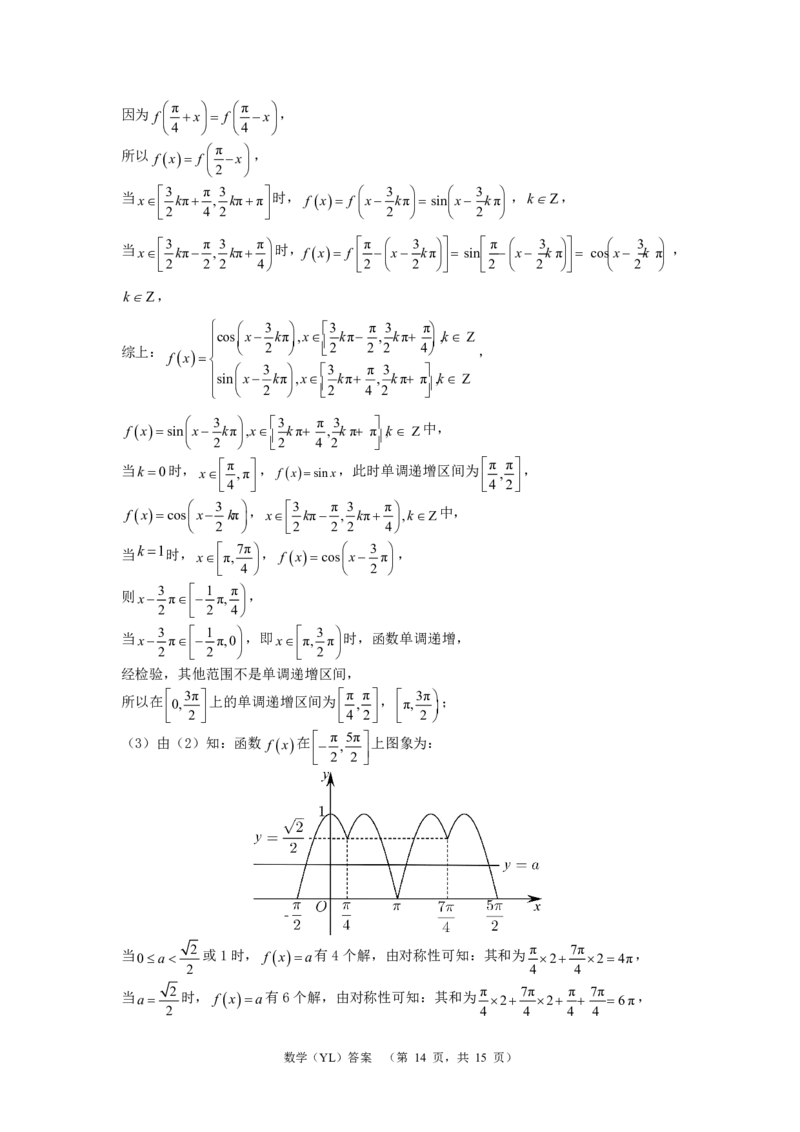
（3）由（2）知：函数 f x在   π , 5π 上图象为：
 
 2 2 
当 0a 2 或1时， f xa有4个解，由对称性可知：其和为 π 2 7π 24π ，
2 4 4
当 a 2 时， f xa有6个解，由对称性可知：其和为 π 2 7π 2 π  7π 6π ，
2 4 4 4 4
数学（YL）答案 （第 14 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#}当 2 a1 时， f xa有8个解，其和为02 π 2 3π 22π28π，
2 2 2
  2
4π,a0, 1

  2 

所以  2 .
S 6π,a
 2
  2 
8π,a ,1
 
  2 

数学（YL）答案 （第 15 页，共 15 页）
{#{QQABaYQEogCgAJBAAAgCAQUwCgMQkBECCCoOAFAMsAAACQNABAA=}#}