文档内容
试题类型:A
秘密★启用前
数学
姓名__________准考证号__________
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在试卷和答题卡指定位置上.
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标
号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将
答案用0.5mm的黑色笔迹签字笔写在答题卡上,写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选
项中,只有一项是符合题目要求的.
1.已知向量 ,且 ,则 ( )
A.1 B.-1 C. D.0
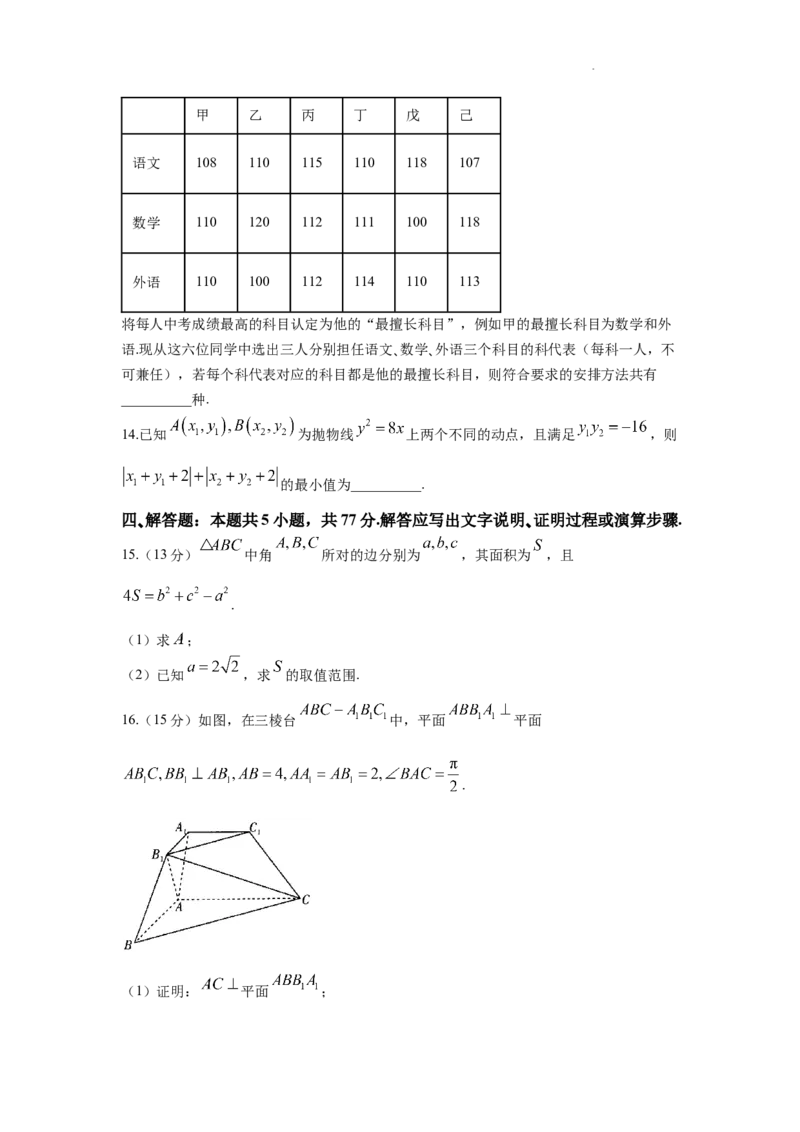
2.已知集合 ,则图中阴影部分表示的集合为( )
A. B. C. D.
3.设命题 ,则 为( )
A. B.
C. D.
4.某学校高三年级组在每次考试后将全年级数学成绩的第85百分位数定为“优秀”分数线.
某次考试后,张老师将自己所带100名学生的数学成绩录入计算机,并借助统计软件制作
成如图所示的频率分布直方图.据此,以样本估计总体,可知此次考试的“优秀”分数线约
为( )
学科网(北京)股份有限公司A.120 B.123 C.126 D.129
5.已知 是椭圆 的左、右焦点,经过 的直线 与椭圆 相
交于 两点,若 ,则椭圆 的离心率为( )
A. B. C. D.
6.已知数列 满足 ,且 ,则 ( )
A. B.-4 C. D.
7.已知函数 是定义在 上不恒为零的函数,若 ,则
( )
A. B.
C. 为偶函数 D. 为奇函数
8.如图,在体积为1的三棱锥 的侧棱 上分别取点 ,使
,记 为平面 、平面 、平面 的
交点,则三棱锥 的体积等于体积等于( )
学科网(北京)股份有限公司A. B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,
有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0
分.
9.已知复数 是 的共轭复数,则( )
A.
B. 的虚部是
C. 在复平面内对应的点位于第二象限
D.复数 是方程 的一个根
10.已知函数 ,则( )
A.当 时,函数 的周期为
B.函数 的对称轴是
C.当 时, 是函数 的一个最大值点
D.函数 在区间 内不单调,则
11.群的概念由法国天才数学家伽罗瓦(1811-1832)在19世纪30年代开创,群论虽起源于
对代数多项式方程的研究,但在量子力学、晶体结构学等其他学科中也有十分广泛的应用.
学科网(北京)股份有限公司设 是一个非空集合,“ ”是一个适用于 中元素的运算,若同时满足以下四个条件,
则称 对“ ”构成一个群:(1)封闭性,即若 ,则存在唯一确定的 ,使
得 ;(2)结合律成立,即对 中任意元素 都有 ;
(3)单位元存在,即存在 ,对任意 ,满足 ,则 称为单位元;
(4)逆元存在,即任意 ,存在 ,使得 ,则称 与 互为逆元,
记作 .一般地, 可简记作 可简记作 可简记作 ,以此类推.正
八边形 的中心为 .以 表示恒等变换,即不对正八边形作任何变换;以
表示以点 为中心,将正八边形逆时针旋转 的旋转变换;以 表示以 所在直线为轴,
将正八边形进行轴对称变换.定义运算“ ”表示复合变换,即 表示将正八边形先进
行 变换再进行 变换的变换.以形如 ,并规定 的变换为元素,
可组成集合 ,则 对运算“ ”可构成群,称之为“正八边形的对称变换群”,记作
.则以下关于 及其元素的说法中,正确的有( )
A. ,且
B. 与 互为逆元
C. 中有无穷多个元素
D. 中至少存在三个不同的元素,它们的逆元都是其本身
三、填空题:本题共3小题,每小题5分,共15分.
12.已知圆柱的底面半径为1,高为2,若圆柱两个底面的圆周都在同一个球的球面上,则
该球的表面积是__________.
13.甲、乙、丙、丁、戊、已六位同学中考语文、数学、外语的成绩如下表:
学科网(北京)股份有限公司甲 乙 丙 丁 戊 己
语文 108 110 115 110 118 107
数学 110 120 112 111 100 118
外语 110 100 112 114 110 113
将每人中考成绩最高的科目认定为他的“最擅长科目”,例如甲的最擅长科目为数学和外
语.现从这六位同学中选出三人分别担任语文、数学、外语三个科目的科代表(每科一人,不
可兼任),若每个科代表对应的科目都是他的最擅长科目,则符合要求的安排方法共有
__________种.
14.已知 为抛物线 上两个不同的动点,且满足 ,则
的最小值为__________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分) 中角 所对的边分别为 ,其面积为 ,且
.
(1)求 ;
(2)已知 ,求 的取值范围.
16.(15分)如图,在三棱台 中,平面 平面
.
(1)证明: 平面 ;
学科网(北京)股份有限公司(2)若直线 与 距离为3,求平面 与平面 夹角的余弦值.
17.(15分)某次比赛中,甲乙二人进入决赛并争夺冠军.比赛规则为:①每局比赛后,胜
者获得3分,负者获得1分,比赛没有平局;②连续2局获胜或积分率先达到11分者可获
得冠军,比赛结束.已知在单局比赛中,甲乙获胜的概率均为 .
(1)求甲乙决出冠军时比赛局数 的分布列与数学期望 ;
(2)求在甲获得冠军的条件下其积分达到11分的概率 .
18.(17分)已知双曲线 经过点 ,其右焦点为 ,且
直线 是 的一条渐近线.
(1)求 的标准方程;
(2)设 是 上任意一点,直线 .证明: 与双曲线 相切于点 ;
(3)设直线 与 相切于点 ,且 ,证明:点 在定直线上.
19.(17分)已知 ,且 ,函数 .
(1)记 为数列 的前 项和.证明:当 时,
;
(2)若 ,证明: ;
(3)若 有3个零点,求实数 的取值范围.
学科网(北京)股份有限公司