文科数学_2024年3月_013月合集_2024届四川省绵阳南山中学高三下学期入学考试_四川省绵阳南山中学2024届高三下学期入学考试文科数学

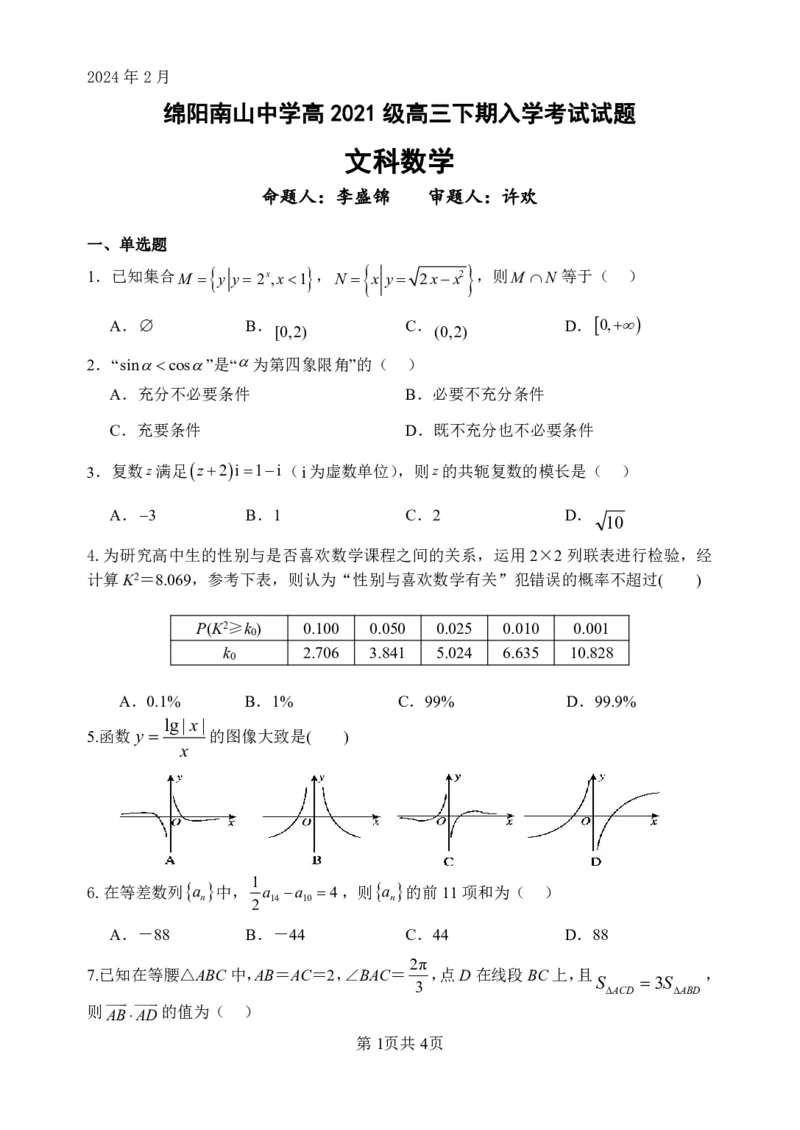
2024年2月 绵阳南山中学高 2021 级高三下期入学考试试题 文科数学 命题人：李盛锦 审题人：许欢 一、单选题 1．已知集合M   y y 2x,x1 ， N   x y 2xx2  ，则M N 等于（ ） A． B． C． D．0, [0,2) (0,2) 2．“sincos”是“ 为第四象限角”的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 3．复数z满足z2i1i（i为虚数单位），则z的共轭复数的模长是（ ） A．3 B．1 C．2 D． 10 4.为研究高中生的性别与是否喜欢数学课程之间的关系，运用2×2列联表进行检验，经 计算K2＝8.069，参考下表，则认为“性别与喜欢数学有关”犯错误的概率不超过( ) P(K2≥k ) 0.100 0.050 0.025 0.010 0.001 0 k 2.706 3.841 5.024 6.635 10.828 0 A．0.1% B．1% C．99% D．99.9% lg|x| 5.函数 y  的图像大致是( ) x 1 6.在等差数列a 中， a a 4，则a 的前11项和为（ ） n 2 14 10 n A．－88 B．－44 C．44 D．88 2π 7.已知在等腰△ABC中，AB＝AC＝2，∠BAC＝ ，点D在线段BC上，且 ， S 3S 3 ACD ABD   则 ABAD 的值为（ ） 第1页共4页2024年2月 7 5 3 1 A． B． C． D． 2 2 2 2 8.平面直角坐标系内，与点A(1,1)的距离为1且与圆(x1)2 (y4)2 2 相切的直线有 （ ） A.4条 B.3条 C.2条 D.0条 9.若函数 f(x) 1 x3 m2 x2(5m)x1的两个极值点都大于 2，则实数m的取值范 3 2 围是（ ） A．,5  5,4 B．,4 C．,2 D． (5,4) 10.如图所示，在三棱锥P­ABC中，已知PA⊥底面ABC，AB⊥BC，E，F分别是线段PB， PC上的动点，则下列说法错误的是( ) A．当AE⊥PB时，△AEF一定为直角三角形 B．当AF⊥PC时，△AEF一定为直角三角形 C．当EF∥平面ABC时，△AEF一定为直角三角形 D．当PC⊥平面AEF时，△AEF一定为直角三角形 5 11.定义在(0,)上的函数 f(x)满足x2f(x)10， f(2) ，则关于x的不等式 2 1 f lnx 2 的解集为（ ） lnx A．(1,e2) B．(0,e2) C．(e,e2) D．(e2,) 2 12.若抛物线y2 2px的焦点为F，点A、B在抛物线上，且AFB ，弦AB的中点M 3 MM' 在准线l上的射影为M '，则 的最大值为（ ） AB 4 3 2 3 3 A． B． C． D． 3 3 3 3 二、填空题 13．已知双曲线 x2  y2 1(m0)的离心率为3，则m . 8 m2 第2页共4页2024年2月 y0 14.设x，y满足约束条件 ，则z2xy的最大值为 ． xy0  xy2 15．将函数 f x 3sin2x2sinxcosx 3cos2x 的图象上所有点的横坐标伸长为原来的 π 的4倍，再将所得图象上所有点向左平移 个单位长度，得到函数g(x)的图象，则g(x)的 3 对称中心为 . 16．在 ABC 中，BC6，AB AC 8，E，F ，G分别为三边BC，CA，AB的中点， 将 AFG ， BEG ，△CEF 分别沿FG，EG，EF 向上折起，使得A，B，C重合，记为P， 则三棱锥PEFG的外接球表面积的最小值为 三、解答题 sinA sinB c2 AB 17.在①  1 ；②(a2b)cosCccosA0；③ 3asin csinA，这 sinB sinA ab 2 三个条作中任选一个，补充在下面的横线上，并解答.在 ABC 中，角A，B，C所对的边 分别为a，b，c，且________________________ (1)求角C的大小； (2)若c4，求AB的中线CD长度的最小值. 18．某公司是一家集无人机特种装备的研发、制造与技术服务的综合型科技创新企业，产 品主要应用于森林消防、物流运输、航空测绘、军事侦察等领域，获得市场和广大观众的 一致好评，该公司生产的甲、乙两种类型无人运输机性能都比较出色，但操控水平需要十 分娴熟，才能发挥更大的作用．该公司分别收集了甲、乙两种类型无人运输机在5个不同 的地点测试的某项指标数x ，y i1,2,3,4,5，数据如下表所示： i i 地点1 地点2 地点3 地点4 地点5 甲型无人运输机指标数x 2 4 5 6 8 乙型无人运输机指标数 3 4 4 4 5 y (1)试求y与x间的相关系数r，并利用r说明y与x是否具有较强的线性相关关系；（若 r 0.75，则线性相关程度很高） 第3页共4页2024年2月 (2)从这5个地点中任抽2个地点，求抽到的这2个地点，甲型无人运输机指标数均高于乙 型无人运输机指标数的概率． n     x  x y  y i i 附：相关公式及数据：r  i1 ， 0.9 0.95． n  2 n  2  x  x  y  y i i i1 i1 19．如图，四棱锥PABCD中，AD//BC ，BCCD，BC 2CD2AD2 2 ，平面 ABCD平面PAC. (1)证明：PC AB； 5 (2)若PAPC  AC，M是PA的中点，求三棱锥CPBM 2 的体积. 20.已知函数 f(x)ex(ex a)a2x，其中参数a0. (1)讨论f(x)的单调性； (2)若f(x)≥0，求a的取值范围 x2 y2 3 21. 已知点P(2,1)在椭圆C:  1(a b0)上,且椭圆的离心率为 . a2 b2 2 （Ⅰ）求椭圆C 的方程； （Ⅱ）过P 作直线l交轨迹C 于另一点 A,求DPAO的面积的取值范围． x22cos 22.在平面直角坐标系 xOy 中,已知曲线 M 的参数方程为 （为参数，  y2sin 02π），点P的坐标为 (2,0) (1)若点Q在曲线M上运动,点N在线段PQ上运动,且 = ,求动点N轨迹的极坐标方程;  π (2)若射线l: 0,0   与曲线M交于点 A （ 异 于 极点），与曲线N交于点B， 0 0 2 且 |OA||OB|2 ,求 0 . 23.已知函数 f(x)|2x1|. (1)求不等式 f(x) x1的解集； b2 a2 (2)若ab1， f(x) f(x1)  对任意正实数a，b恒成立，求实数x的取值范围. a b 第4页共4页