文科数学答案_2024年3月_02按日期_17号_2024届内蒙古呼和浩特市高三第一次质量监测_2024届内蒙古呼和浩特市高三下学期第一次质量数据监测（一模）文科数学

呼和浩特市高三文科数学一模参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10 11 12
B D B A A C A C B C B D
二、填空题
3 7
13、 14、
4 9
15、24 16、x4
三、解答题
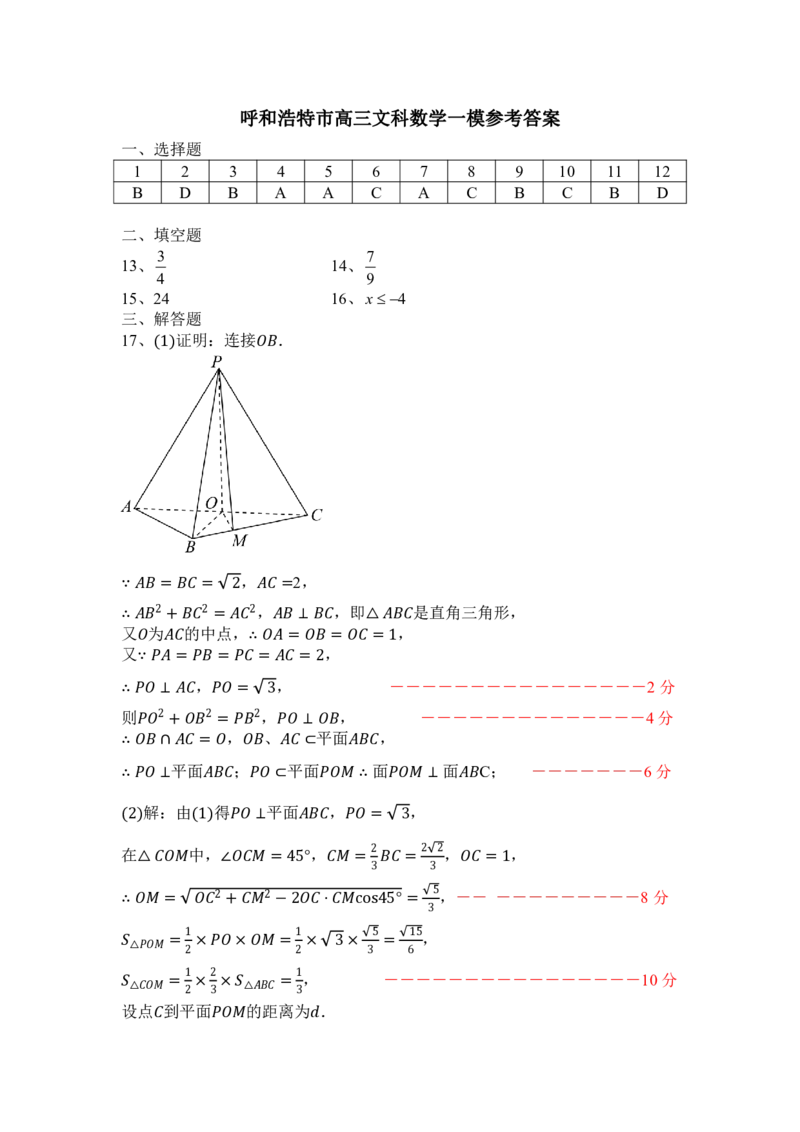
17、 证明：连接 ．
(1)  
， 2，
， ，即 是直角三角形，
∵   =   = 2   =
又 为2 的中2 点，2 ，
∴   +   =     ⊥   △   
又 ，
∴   =   =   = 1
∵   = 
，
=   = 
，
= 2
－－－－－－－－－－－－－－－－2分
∴
则
⊥     =
，
3
， －－－－－－－－－－－－－－4分
2 2 ， 2、 平面 ，
+   =     ⊥  
∴   ∩
平

面
= 
；

平

面
⊂   
面 面 C； －－－－－－－6分
∴   ⊥      ⊂    ∴    ⊥  
解：由 得 平面 ， ，
(2) (1)   ⊥      = 3
在 中， ， ， ，
2 2 2
△    ∠    = 45°   = 3   = 3，－   － = － 1 －－－－－－－－8分
5
2 2
∴   =   +   −2   ⋅   cos45° = ，3
1 1 5 15
△    = 2×   ×   = 2，× 3× 3 =－－6－－－－－－－－－－－－－－10分
1 2 1
设△点    到 = 平 2× 面 3×  △的   距  离 = 为 3 ．

{#{QQABDYKAggCoQBBAAAgCAwHKCAAQkAACCAoOwAAAsAAASQNABCA=}#}由 ，可得 ，
1 1
−    =   −    3×  △    ×   = 3×  △    ⋅ 
解得 ，
2 5
点  到 = 平面5 的距离为 ． －－－－－－－－－－－－－－－－12分
2 5
∴18、  解：（1）   C  为事件：“乙5农药残留在表面的百分比不低于5.5”，
根据直方图得到
P
（C）的估计值为0.70．
a0.200.150.7
则由频率分布直方图得： ，

0.05b0.1510.7
解得乙农药残留在表面的百分比直方图中 a0.35 ， b0.10 ． －－－－－4分
（答b0.1的扣一分）
（2）估计甲农药残留百分比的平均数为：
x 20.1530.2040.3050.2060.1070.054.05 ．－－－－－－－8分
甲
（3）设乙农药残留百分比的中位数为

解得 6.07 －－－－－－12分
0.05+0.10+0.15 ×1+0.35×  −5.5 = 0.5
19、因为 ，
≈
2
所以 Sn +Sn+1 = 2n +6n+3 ．
2
两式S相 n+ 减 2 ，+得Sn+1 = 2 n+1 +6 n+,1n+N*3.
所以 an+2 +an+1 = 4 n+2 ； －－－－4分
（2） S9由 = （ a11） + 知 a2 +a3 + a4 +a5 +⋯ ① + ， a8 +a9 = 99
可得 an+2 +an+②1 =，4nn2+．2
因为an +an，+1 = 4 n+1 ，
所以 a1 = 3 ， S 又2 +S1 = 11 ，
所以 a2 = 5 S3 +S2 = 23 = 2a1 +2a2 +a3
又由a①3②=得7 a a 4,n2． －－－－8分
n2 n
所以 ，即 ，n为偶数，
则当an2n3=，a且2 +为4奇n数−时1，= 4n+1 an = 2n+1
，
an = 4 n+1 −an+1 = 4 n+1 − 2 n+1 +1 = 2n+1
{#{QQABDYKAggCoQBBAAAgCAwHKCAAQkAACCAoOwAAAsAAASQNABCA=}#}又 , 符合上式，综合得 ． －－－－12分
a1 = 3 a3 = 7 an = 2n+1
20、解： f(x)的定义域为R
(1) f (x)  (x1)ex 2x2  (x1)(ex 2),xR --------1分
当x1或xln2时， f (x)  0, f(x)在(1,)上单调递增；
当ln2x x1时， f (x) 0, f(x)在(ln2,1)上单调递减；
所以， f(x)的增区间是(,ln2)和(1,)， f(x)的减区间是（ln2，1） . --------4 分
（2）由(1)知：g(x)  f (x)  (x1)(ex 2),xR
g(x)  xex 2,xR，g(ln2)  ln2eln2 2  2ln22
又g(ln2)  (ln21)(eln2 2)  0，所以，
g(x) 在 x  ln2 处的切线方程 l 为y  (2ln22)(xln2) ------------6 分
令h(x)  g(x)(2ln22)(xln2)  (x1)(ex 2)(2ln22)(xln2),xR，
则h(x)  xex 2ln2,xR， h(x)  (x1)ex,xR
当x  1时，h(x)  0，h(x)在(1,)上单调递增；
当x  1时，h(x)  0，h(x)在(1,)上单调递减；
所以，当x  1时，h(x)取得最小值h(1)  e1 2ln2 0 ----------8 分
当x时，h(x)0，
h(1)  e2ln2  0,h(ln2)  ln2eln2 2ln2  0 ------------10 分
故
当x  ln2时，h(x)  0，h(x)在(ln2,)上单调递增；
当x  ln2时，h(x) 0，h(x)在(，ln2)上单调递减；
因此，
当x  ln2时，h(x)取得最小值h(ln2)  0，
即：h(x) 0，g(x) 的图象在直线 l 的上方。 ----------12 分
{#{QQABDYKAggCoQBBAAAgCAwHKCAAQkAACCAoOwAAAsAAASQNABCA=}#}2 2
 p  p p
21.(1)解：令R(x，y)，则RF  x2 y   2py y2    py  y
 2  2 2
p p p p
因为y0，所以y  ，RF的最小值为 ，即 1，抛物线的方程为x2 4y
2 2 2 2
4分
2 1 1
(2)三者关系为：   1分
PF PM PN
1(1) 2
证明：令M(x，y )，N(x，y )，l : y1k(xm)，k  
1 1 2 2 PF 0m m
2 1 1 2 1 1
则     
PF PM PN 1 1 1
     
1 1(1) 1 y (1) 1 y (1)
k2 k2 1 k2 2
2 1 1
  
     
1(1) y (1) y (1)
1 2
1 1 y  y 2
1   1 2
  
y 1 y 1 y 1 y 1
1 2 1 2
  
 y  y 2 y 1 y 1
1 2 1 2
 y y 1 9分
1 2
 2
l : y1 (xm) 16
联立  PF m 得y2 (2 )y10，由韦达定理得y y 1
m2 1 2
 x2 4y
2 1 1
综上所述：  
PF PM PN
12分
22解：
（1）设P点的极坐标为(,)，－－－－－－－－－－－－－－－－－－1分
3 3
则 OP ,cos ,OM 
OM cos
OM OP 12
3
 12 4cos－ －－－－－－－－－－－－－－－－4分
cos

4cos，0 －－－－－－－－－－－－－ －－－5分
2
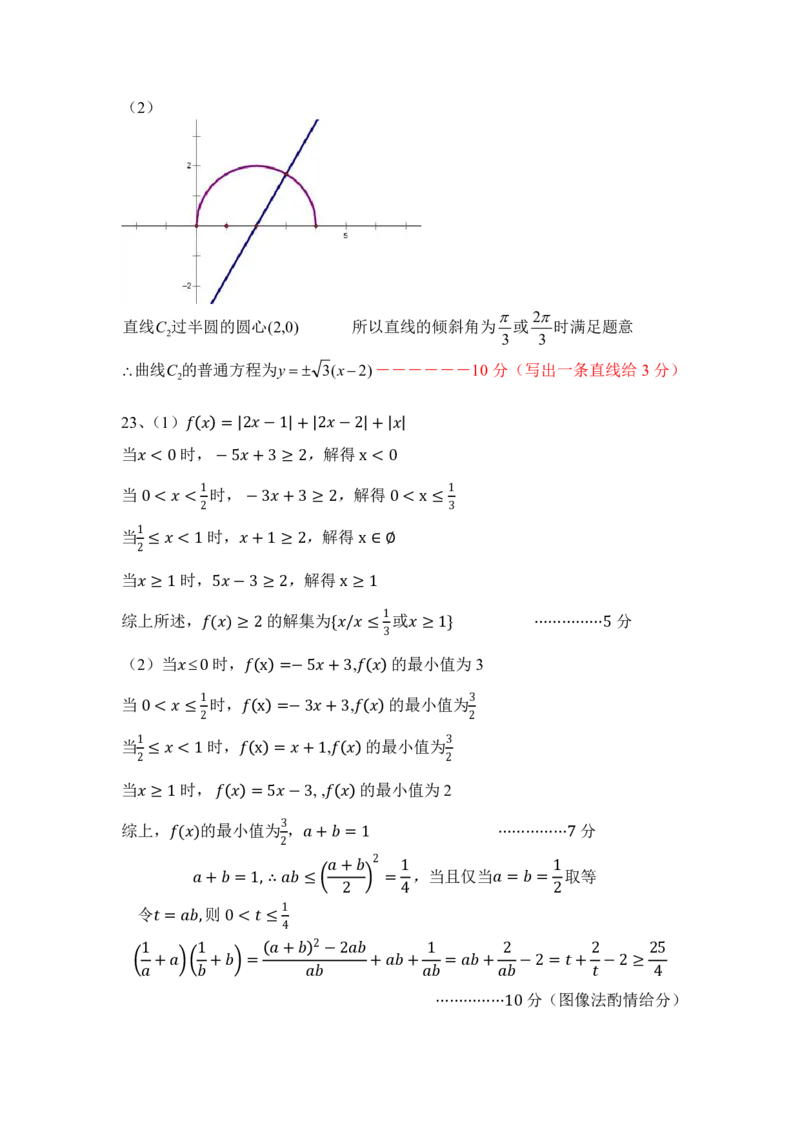
{#{QQABDYKAggCoQBBAAAgCAwHKCAAQkAACCAoOwAAAsAAASQNABCA=}#}（2）
 2
直线C 过半圆的圆心(2,0) 所以直线的倾斜角为 或 时满足题意
2 3 3
曲线C 的普通方程为y  3(x2)－－－－－－10分（写出一条直线给3分）
2
23、（1）
当 时， ，解得
= 2  −1 + 2  −2 + 
当  < 0 时−，5  +3 ≥ 2 ，解x得< 0
1 1
当 0 <  < 2时， −3  +3 ， ≥ 解 2 得 0 < x ≤ 3
1
2 ≤  < 1  +1 ≥ 2 x ∈ ∅
当 时， ，解得
综  上≥所1述， 5  −3 ≥的2解集为 x ≥ 1 或 分
1
(  ) ≥ 2 {  /  ≤ 3  ≥ 1} ⋯⋯⋯⋯⋯5
（2）当  时， , 的最小值为3
当  0时，  x =−5  +3 ,   的最小值为
1 3
当 0 <  ≤ 2时，  x =−3  + , 3  的  最小值为 2
1 3
2 ≤  < 1  x =  +1   2
当 时， ,, 的最小值为2
综  上≥，1 的  最  小值=为5  ，−3   分
3
(  ) 2  +  = 1 ⋯⋯⋯⋯⋯7
，当且仅当 取等
2
+  1 1
令  则+  = 1, ∴   ≤ =  =  =
2 4 2
1
=   , 0 <  ≤ 4
2
1 1  +  −2   1 2 2 25
+  +  = +   + =   + −分2（=图  像+法−酌2情≥给分）
4
⋯⋯⋯⋯⋯10
{#{QQABDYKAggCoQBBAAAgCAwHKCAAQkAACCAoOwAAAsAAASQNABCA=}#}