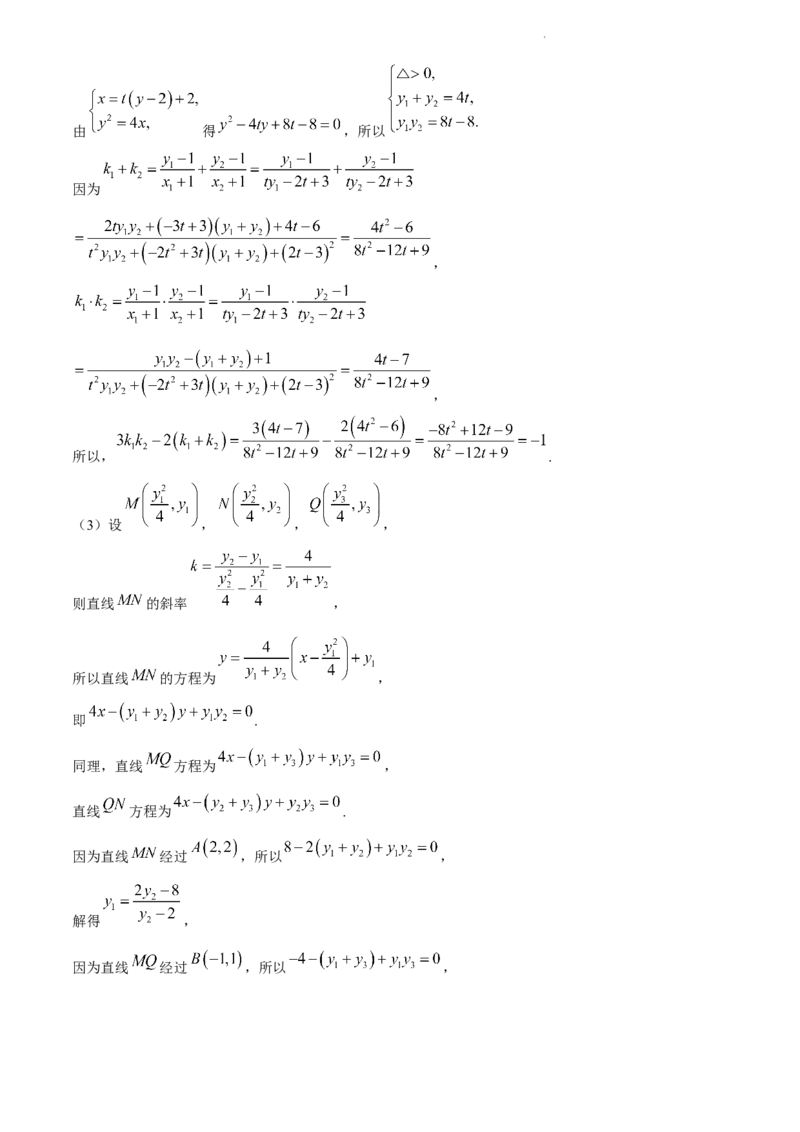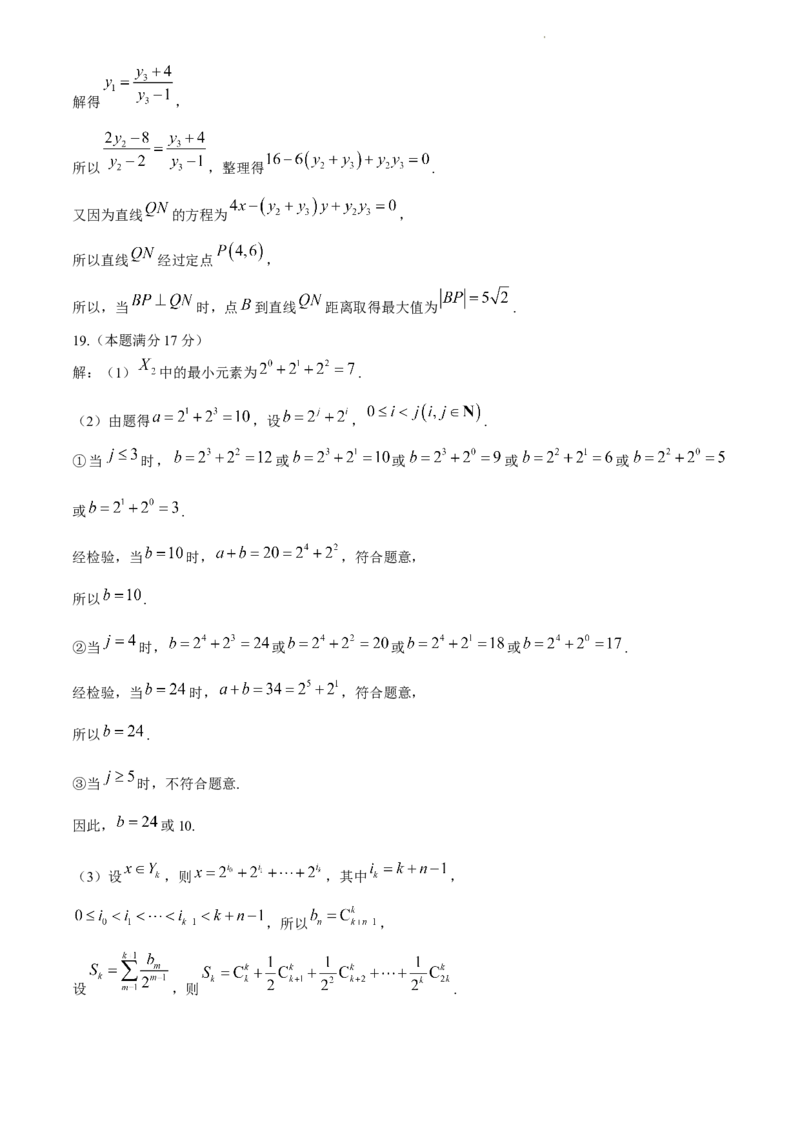文档内容
浙江省高考科目考试绍兴市适应性试卷
(2024年4月)
数学试题
本科试题卷分选择题和非选择题两部分,全卷共 6页,选择题部分1至3页,非选择题部分3
至6页,满分150分,考试时间120分钟。
考生注意:
1.答题前,请务必将自己的学校、班级、姓名、座位号用黑色字迹的签字笔或钢笔分别填写
在试题卷和答题纸规定的位置上。
2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试
题卷上的作答一律无效。
一、选择题(本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一
项是符合题目要求的)
1.已知 ,则 ( )
A. B.3 C. D.5
2.已知椭圆 的离心率为 ,长轴长为4,则该椭圆的短轴长为( )
A. B. C. D.
3.已知等差数列 的前 项和为 ,且 ,则 ( )
A.9 B.10 C.11 D.12
4.已知四边形 是平行四边形, , ,记 , ,则
( )
A. B.
C. D.
5.过点 作圆 的切线 , 为切点, ,则 的最大值是( )
A. B. C. D.
6.已知 , ,则 ( )
学科网(北京)股份有限公司A. B. C. D.
7.在边长为4的正三角形 中,E,F分别是 , 的中点,将 沿着 翻折至 ,
使得 ,则四棱锥 的外接球的表面积是( )
A. B. C. D.
8.已知点A,B,C都在双曲线 : 上,且点A,B关于原点对称, .
过A作垂直于x轴的直线分别交 , 于点M,N.若 ,则双曲线 的离心率是( )
A. B. C.2 D.
二、选择题(本大题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合
题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.国家统计局统计了2024年1月全国多个大中城市二手住宅销售价格的分类指数,其中北方和南方各4个
城市的90m²及以下二手住宅销售价格的环比数据如下:
北 方 城 环比(单位:%,上月=100) 南方城市 环比(单位:%,上月=100)
市
北京 99.5 上海 99.5
天津 99.6 南京 99.5
石家庄 99.6 南昌 99.6
沈阳 99.7 福州 99.8
则( )
A.4个北方城市的环比数据的极差小于4个南方城市的环比数据的极差
B.4个北方城市的环比数据的均值小于4个南方城市的环比数据的均值
C.4个北方城市的环比数据的方差大于4个南方城市的环比数据的方差
D.4个北方城市的环比数据的中位数大于4个南方城市的环比数据的中位数
10.已知等比数列 的公比为 ,前 项和为 ,前 项积为 ,且 , ,则( )
A.数列 是递增数列 B.数列 是递减数列
C.若数列 是递增数列,则 D.若数列 是递增数列,则
11. 已 知 定 义 在 上 的 函 数 在 区 间 上 单 调 递 增 , 且 满 足 ,
,则( )
学科网(北京)股份有限公司A. B.
C. D.
三、填空题(本大题共3小题,每小题5分,共15分)
12. 的展开式中 的系数是___________.(用数字作答)
13.已知集合 , ,且 有 4 个子集,则实数 的最小值是
___________.
14.已知函数 ,若 , , ,则实数 的取值范
围是__________.
四、解答题(本大题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤)
15.(13分)
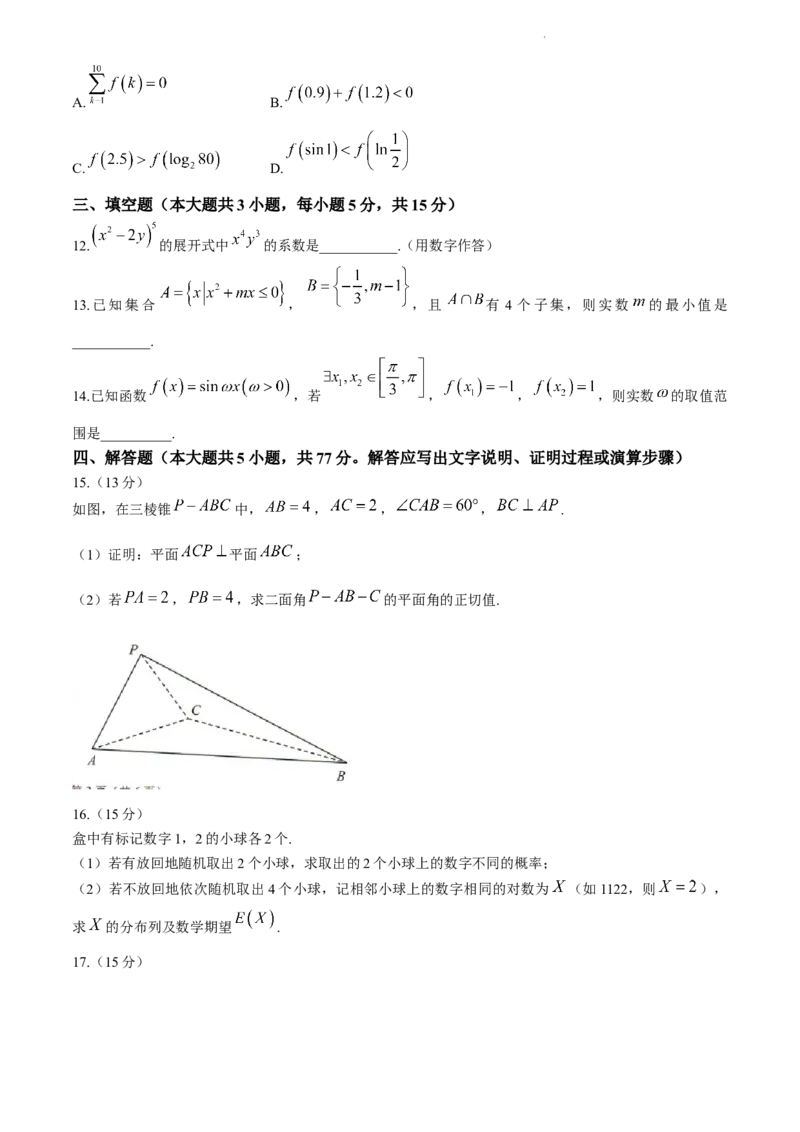
如图,在三棱锥 中, , , , .
(1)证明:平面 平面 ;
(2)若 , ,求二面角 的平面角的正切值.
16.(15分)
盒中有标记数字1,2的小球各2个.
(1)若有放回地随机取出2个小球,求取出的2个小球上的数字不同的概率;
(2)若不放回地依次随机取出4个小球,记相邻小球上的数字相同的对数为 (如1122,则 ),
求 的分布列及数学期望 .
17.(15分)
学科网(北京)股份有限公司已知函数 .
(1)当 时,求曲线 在点 处的切线方程;
(2)当 时, ,求实数 的取值范围.
18.(17分)
已知抛物线 : 的焦点到准线的距离为2,过点 作直线交 于M,N两点,点
,记直线 , 的斜率分别为 , .
(1)求 的方程:
(2)求 的值;
(3)设直线 交C于另一点Q,求点B到直线 距离的最大值.
19.(17分)
已知 ,集合 .
(1)求 中最小的元素;
(2)设 , ,且 ,求 的值;
(3)记 , ,若集合 中的元素个数为 ,求 .
学科网(北京)股份有限公司浙江省高考科目考试绍兴市适应性试卷
(2024年4月)
数学参考答案及评分标准
一、选择题(本大题共8小题,每小题5分,共40分)
1.C 2.B 3.D 4.A 5.D 6.B 7.C 8.B
二、选择题(本大题共3小题,每小题6分,共18分。全部选对的得6分,部分选对的得3
分,有选错的得0分)
9.AD 10.ACD 11.BCD
三、填空题(本大题共3小题,每小题5分,共15分)
12.-80 13. 14. 或
四、解答题(本大题共5小题,共77分)
15.(本题满分13分)
(1)证明:在 中,由余弦定理得 ,
所以 ,所以 ,
又 , ,所以 平面 ,
又 平面 ,
所以平面 平面 .
(2)解法1:过点 作 交 于点 ,
因为平面 平面 ,平面 平面 ,
所以 平面 .
过点 作 交 于点 ,连接 ,则 ,
所以 是二面角 的平面角.
由(1)知, ,所以 ,
又 ,所以,三角形 是正三角形,
所以, , .
在直角三角形 中, ,
学科网(北京)股份有限公司所以 .
所以,二面角 的平面角的正切值是2.
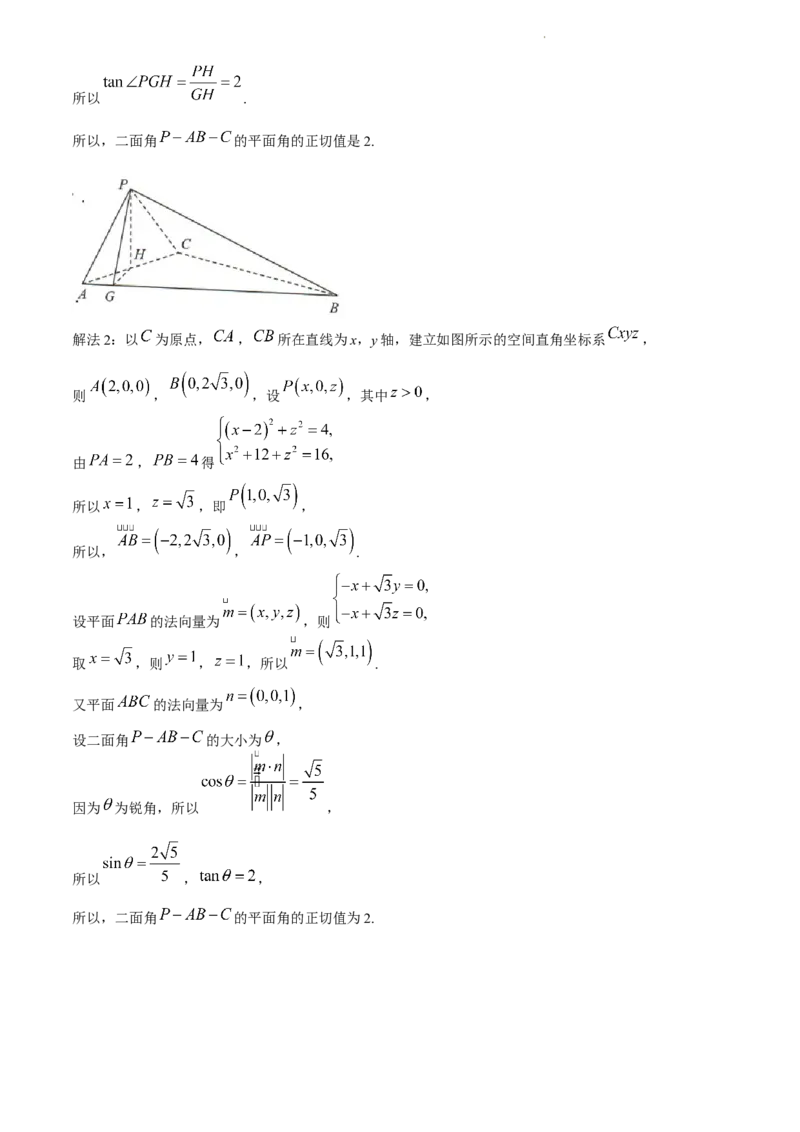
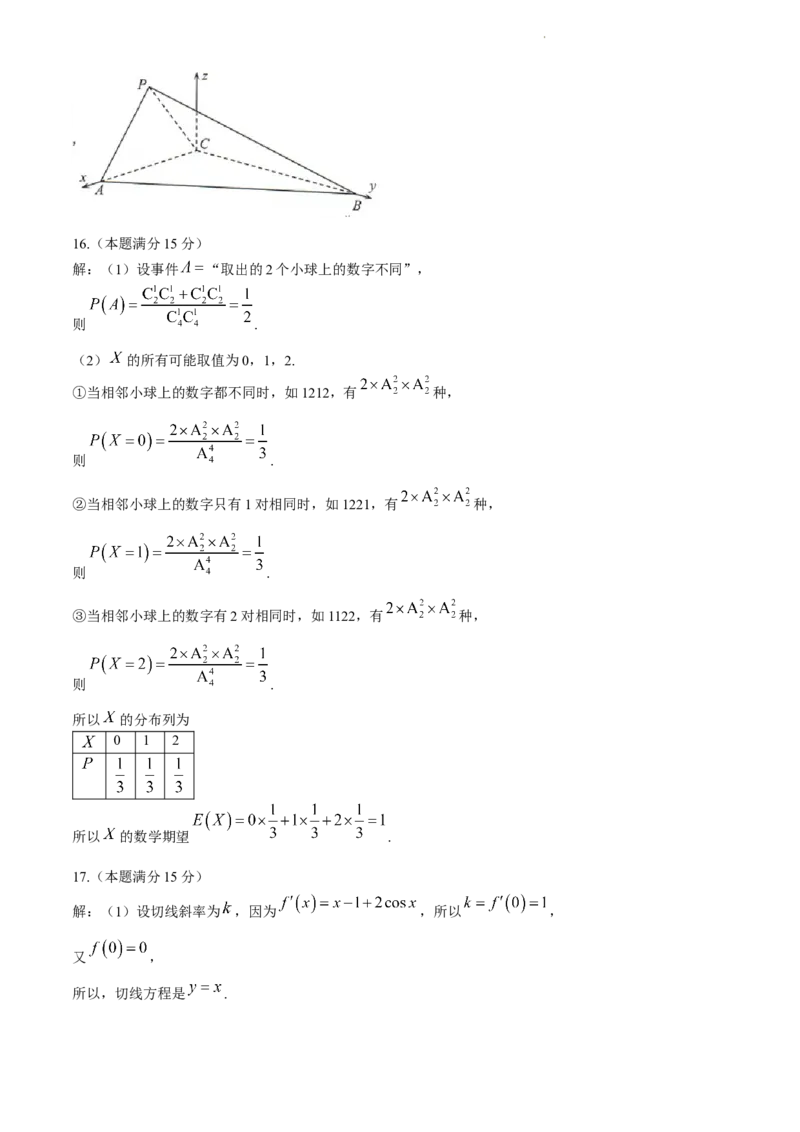
解法2:以 为原点, , 所在直线为x,y轴,建立如图所示的空间直角坐标系 ,
则 , ,设 ,其中 ,
由 , 得
所以 , ,即 ,
所以, , .
设平面 的法向量为 ,则
取 ,则 , ,所以 .
又平面 的法向量为 ,
设二面角 的大小为 ,
因为 为锐角,所以 ,
所以 , ,
所以,二面角 的平面角的正切值为2.
学科网(北京)股份有限公司16.(本题满分15分)
解:(1)设事件 “取出的2个小球上的数字不同”,
则 .
(2) 的所有可能取值为0,1,2.
①当相邻小球上的数字都不同时,如1212,有 种,
则 .
②当相邻小球上的数字只有1对相同时,如1221,有 种,
则 .
③当相邻小球上的数字有2对相同时,如1122,有 种,
则 .
所以 的分布列为
0 1 2
所以 的数学期望 .
17.(本题满分15分)
解:(1)设切线斜率为 ,因为 ,所以 ,
又 ,
所以,切线方程是 .
学科网(北京)股份有限公司(2)①当 时,因为 ,所以 ,
所以 .
记 ,则 , .
因为当 时, ,所以 在区间 上单调递增,
所以, ,
所以, 在区间 上单调递增,
所以, ,所以 .
②当 时, ,
因为当 时, ,所以 ,
所以 在区间 上单调递增.
因为 , ,
所以,存在 ,使得 ,
所以,当 时, ,即 在区间 上单调递减,
所以 ,不满足题意.
综上可知, .
18.(本题满分17分)
解:(1)因为焦点到准线的距离为2,所以 ,
所以抛物线 的方程为 .
(2)设 , ,直线 的方程为 ,
学科网(北京)股份有限公司由 得 ,所以
因为
,
,
所以, .
(3)设 , , ,
则直线 的斜率 ,
所以直线 的方程为 ,
即 .
同理,直线 方程为 ,
直线 方程为 .
因为直线 经过 ,所以 ,
解得 ,
因为直线 经过 ,所以 ,
学科网(北京)股份有限公司解得 ,
所以 ,整理得 .
又因为直线 的方程为 ,
所以直线 经过定点 ,
所以,当 时,点 到直线 距离取得最大值为 .
19.(本题满分17分)
解:(1) 中的最小元素为 .
(2)由题得 ,设 , .
①当 时, 或 或 或 或
或 .
经检验,当 时, ,符合题意,
所以 .
②当 时, 或 或 或 .
经检验,当 时, ,符合题意,
所以 .
③当 时,不符合题意.
因此, 或10.
(3)设 ,则 ,其中 ,
,所以 ,
设 ,则 .
学科网(北京)股份有限公司因为 ,
所以
.
因为 ,
所以 ,所以 ,
又因为 ,所以 .
学科网(北京)股份有限公司