海南省四校（海南中学、海口一中、文昌中学、嘉积中学）2024届高三下学期一模试题数学(1)(1)_2024年4月_024月合集_2024届海南省四校高三下学期一模试题

海南中学､海口一中､文昌中学､嘉积中学
2024 届高三联考试题
数学
时间：120分钟 满分：150分
注意事项：
1.答卷前，考生务必将自己的姓名､准考证号填写在答题卡上.
2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑；如需改
动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上，写在试
卷上无效.
3.考试结束后，本试卷和答题卡一并交回.
第 I 卷选择题
一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是
符合题目要求的.
1.已知集合A  x∣x2 6x70  , B{x∣x3 1}，则AB（ ）
A.
1,24,7
B.
1,7
C.
1,24,7
D.
2,4
2.若古典概型的样本空间1,2,3,4 ，事件A1,2 ，事件A,B相互独立，则事件B可以是（ ）
A.
1,3
B.
1,2,3
C.
3,4
D.
2,3,4
3.已知,是两个不同的平面，m,n是两条不同的直线，则下列命题错误的是（ ）
A.如果∥,n，那么n∥
B.如果m,n∥，那么mn
C.如果m ∥n,m，那么n 
D.如果mn,m,n∥，那么
4.在锐角VABC中，角A,B,C的对边分别为a,b,c，且a 3,A60o，则b 的取值范围是（ ）
     
A. 0,6 B. 0,2 3 C. 3,2 3 D. 3,6
π 
5.已知直线l:2x3y10的倾斜角为，则cosπsin    （ ）
2 
9 9 6 6
A. B. C. D.
13 13 13 136.英国数学家贝叶斯在概率论研究方面成就显著，根据贝叶斯统计理论，随机事件A,B存在如下关系：
PAPB∣A
PA∣B
.若某地区一种疾病的患病率是0.05，现有一种试剂可以检验被检者是否患病.
PB
已知该试剂的准确率为95%，即在被检验者患病的前提下用该试剂检测，有95%的可能呈现阳性；该试
剂的误报率为0.5%，即在被检验者未患病的情况下用该试剂检测，有0.5%的可能会误报阳性.现随机抽
取该地区的一个被检验者，已知检验结果呈现阳性，则此人患病的概率为（ ）
495 995 10 21
A. B. C. D.
1000 1000 11 22
6
7.已知三棱锥OABC的体积是 ,A,B,C是球O的球面上的三个点，且ACB120o，
6
AB 3,ACBC 2，则球O的表面积为（ ）
A.36π B.24π C.12π D.8π
8.已知过抛物线C: y2 2px(p 0)焦点F 的直线交C于A,B两点，点A,B在C的准线上的射影分别为
点A,B ，线段AB的垂直平分线l的倾斜角为120o，若 AB 4，则 p （ ）
1 1 1 1
1
A. B.1 C.2 D.4
2
二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目
要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分.
3 1
9.若z   i（i为虚数单位），则下列说法正确的为（ ）
2 2
A. z 1 B.zz  z2 C.z3 i D.z2 z2024 0
 π
10.已知函数 f xsin  x  (0)，则下列说法正确的是（ ）
 6
5π 
A.若1，则 ,0 是 f x 的图象的对称中心
 6 
π
B.若 f x f  恒成立，则的最小值为2
6
 π 2
C.若 f x 在

0,

上单调递增，则0
 2 3
11 17
D.若 f x 在 0,2π 上恰有2个零点，则 
12 12
11.已知定义在R上的奇函数 f x ，满足 f 2x1 f 32x ，当x0,1 时， f x x，则下列结论正确的是（ ）
A.函数 f x 的最小正周期为6
B.函数 f x 在 2024,2025 上递增
22
C.  f(k)1
k1
D.方程 f xlog x 有4个根
5
第 II 卷非选择题
三､填空题：本题共 3小题，每小题 5分，共 15分.
r r r r r r r r
12.已知向量a,b 满足|a|1,|b |3,ab (2, 6)，则 3ab __________.
13.设等差数列 a  的前n项和为S ，若a a 10,S 42，则S __________.
n n 3 5 6 10
uuur uuur
14.在VABC中，A3,0,B3,0,CD AB于D，若H为VABC的垂心，且CD9CH .则H到直线
x 2y80距离的最小值是__________.
四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤.
15.（本小题满分13分）
远程桌面连接是一种常见的远程操作电脑的方法，除了windows系统中可以使用内置的应用程序，通过输
入IP地址等连接到他人电脑，也可以通过向日葵，anyviewer等远程桌面软件，双方一起打开软件，通过
软件随机产生的对接码，安全的远程访问和控制另一台电脑.某远程桌面软件的对接码是一个由“1,2,3”这
3个数字组成的五位数，每个数字至少出现一次.
（1）求满足条件的对接码的个数；
（2）若对接码中数字1出现的次数为X ，求X 的分布列和数学期望.
16.（本小题满分15分）
已知函数 f x x2 alnx1,aR.
（1）当a1时，求曲线y  f x 在点  1, f 1 处的切线方程；
（2）当a 0时，若函数 f x 有最小值2，求a的值.
17.（本小题满分15分）
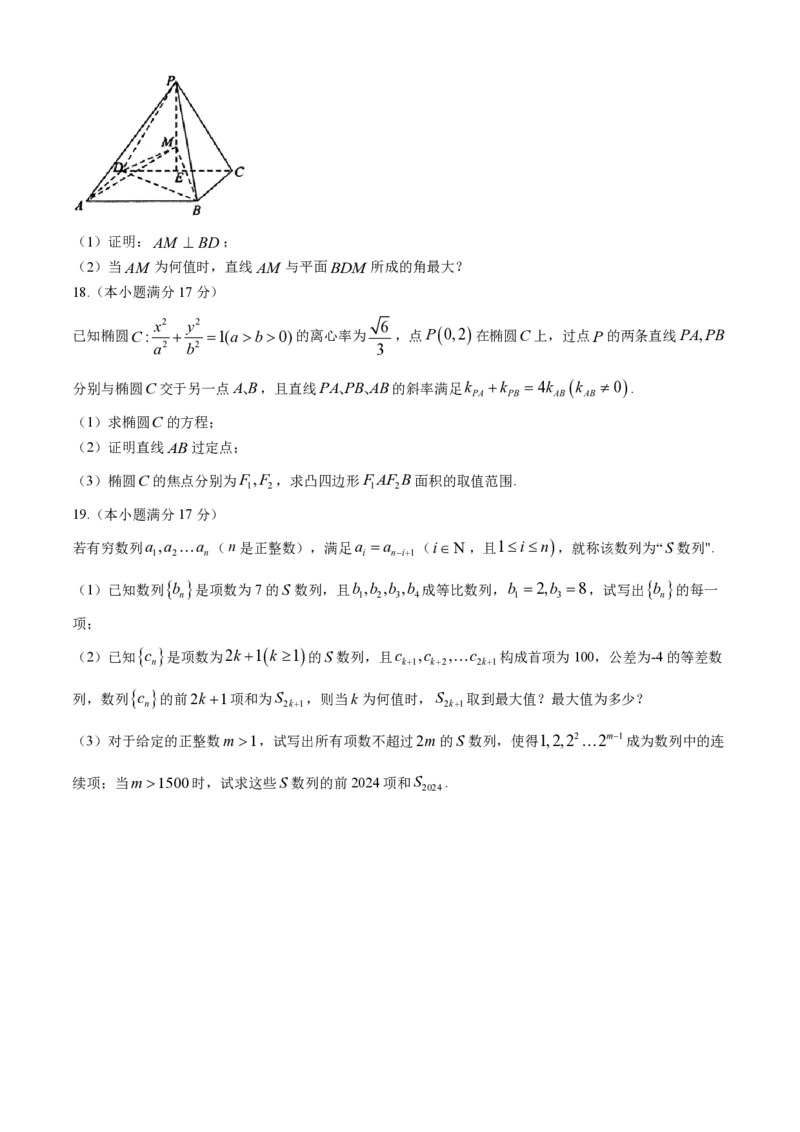
如图，四棱锥PABCD的底面为矩形，平面PCD平面ABCD,VPCD是边长为2等边三角形，
BC  2，点E为CD的中点，点M 为线段PE上一点（与点P,E 不重合）.（1）证明：AM  BD；
（2）当AM 为何值时，直线AM 与平面BDM 所成的角最大？
18.（本小题满分17分）
x2 y2 6
已知椭圆C:  1(a b0)的离心率为 ，点P0,2 在椭圆C上，过点P的两条直线PA,PB
a2 b2 3
分别与椭圆C交于另一点A､B，且直线PA､PB､AB的斜率满足k k 4k k 0 .
PA PB AB AB
（1）求椭圆C的方程；
（2）证明直线AB过定点；
（3）椭圆C的焦点分别为F,F ，求凸四边形FAF B面积的取值范围.
1 2 1 2
19.（本小题满分17分）
若有穷数列a ,a a （n是正整数），满足a a （iN，且1in ，就称该数列为“S数列".
1 2 n i ni1
（1）已知数列 b  是项数为7的S数列，且b,b ,b ,b 成等比数列，b 2,b 8，试写出 b  的每一
n 1 2 3 4 1 3 n
项；
（2）已知 c  是项数为2k1k 1 的S数列，且c ,c ,c 构成首项为100，公差为-4的等差数
n k1 k2 2k1
列，数列 c  的前2k 1项和为S ，则当k 为何值时，S 取到最大值？最大值为多少？
n 2k1 2k1
（3）对于给定的正整数m 1，试写出所有项数不超过2m的S数列，使得1,2,222m1成为数列中的连
续项；当m1500时，试求这些S数列的前2024项和S .
2024海南中学､海口一中､文昌中学､嘉积中学
2024 届高三联考题答案
数学
第 I 卷选择题
一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是
符合题目要求的.
题号 1 2 3 4 5 6 7 8
答案 A A D C B C A B
二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目
要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分.
题号 9 10 11
答案 ACD ABC BC
第 II 卷非选择题
三､填空题：本题共 3小题，每小题 5分，共 15分.
12.3 2 13.10 14. 3
四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤.
15.解：（1）当对接码中一个数字出现3次，另外两个数字各出现1次时，
C1A5 354321
种数为： 3 5  60，
A3 321
3
当对接码中两个数字各出现2次，另外一个数字出现1次时，
C2A5 354321
种数为： 3 5  90，
A2A2 2121
2 2
所有满足条件的对接码的个数为150.
（2）随机变量X 的取值为1,2,3，其分布列为：
C1A5 C2A5 C1A5
2 5  2 5 2 5
A3 A2A2 7 A2A2 6 2
PX 1 3 2 2  ,PX 2 2 2  
150 15 150 15 5
A2 2
PX 3 5 
150 15
故概率分布表为：X 1 2 3
7 2 2
P
15 5 15
7 2 2 5
故EX1 2 3  .
15 5 15 3
16.解：（1）当a1时， f x x2 lnx1,y  f x 的定义域为 0, ，
1 1
则 fx2x ，则 f12 1, f 11ln112，
x 1
由于函数 f x 在点  1, f 1 处切线方程为y2 x1，即y  x1.
（2） f x x2 alnx1,aR的定义域为 0, ，
a 2x2 a
fx2x  ，
x x
a a
当a 0时，令
fx0，解得：x
；令
fx0，解得：0
x ，
2 2
 a   a 
所以 f x 在0, 上单调递减，在 ,上单调递增，
   
2 2
   
 a  a a a a a
所以， f(x)  f   aln 12，即  ln 10
min  2  2 2 2 2 2
 
a
则令t  0，设gtttlnt1,gtlnt，
2
令gt0，解得：t 1；令gt0，解得：0t
1，
所以gt
在
0,1
上单调递增，在
1,
上单调递减，
所以gt g11ln110，
a
所以t  1，解得：a  2.
2
（不说明唯一性猜a值扣3分）
17.（1）证明：连接AE，因为VPCD是等边三角形，且E是DC 中点，
所以PE CD，又因为PE 平面PCD，平面PCD平面ABCD，
平面PCD平面ABCDCD，
所以PE 平面ABCD，
又因为BD面ABCD，所以BD PE
DE AD
因为DE 1,AD 2,AB2,  ，
AD AB
所以RtVEDA∽RtVDAB,DAE ABD，
π
所以BAEABD ，即AE  BD，
2
因为BD PE,AEPE  E,AE 平面PAE,PE 平面PAE，
所以BD平面PAE，
又因为AM 平面PAE，所以BD AM
另证：（1）因为三角形PCD是等边三角形，且E是DC 中点，
所以PE CD，
又因为PE 平面PCD，平面PCD平面ABCD，
平面PCD平面ABCDCD，
所以PE 平面ABCD
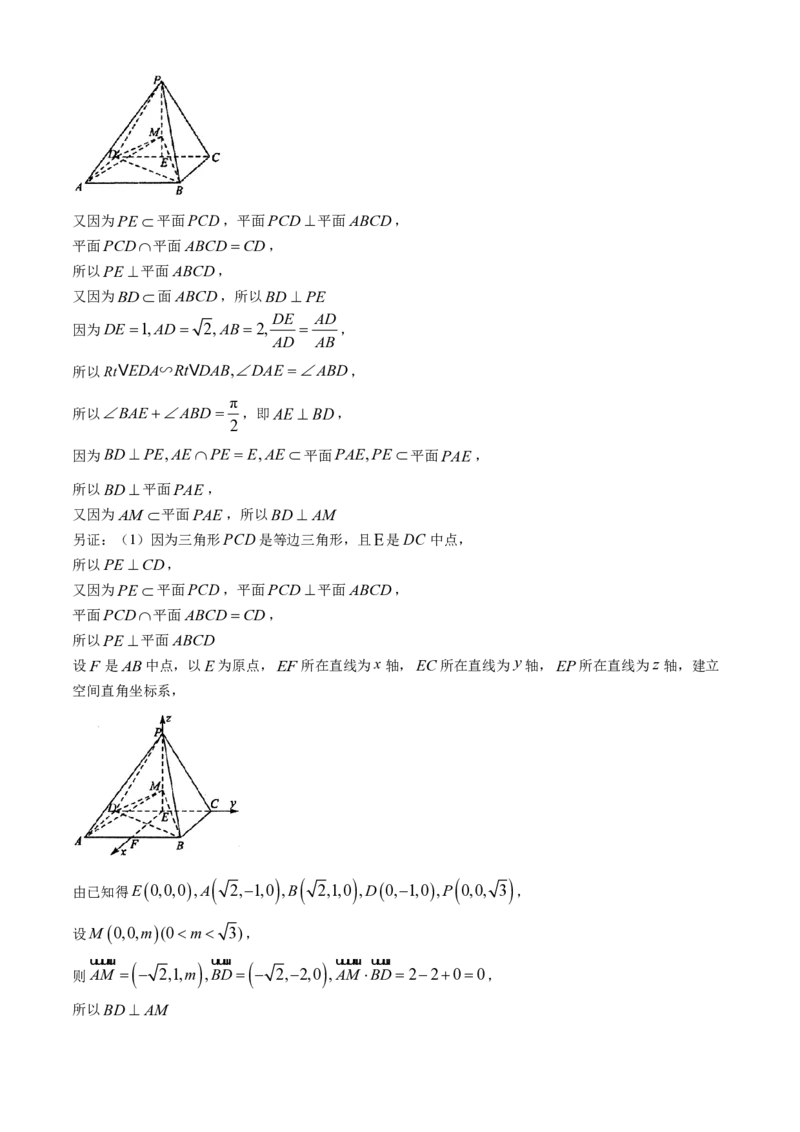
设F 是AB中点，以E为原点，EF所在直线为x轴，EC所在直线为y轴，EP所在直线为z 轴，建立
空间直角坐标系，
     
由已知得E0,0,0,A 2,1,0 ,B 2,1,0 ,D0,1,0,P 0,0, 3 ，
设M 0,0,m(0m 3)，
uuuur uuur uuuur uuur
   
则AM   2,1,m ,BD  2,2,0 ,AM BD2200，
所以BD AM（2）解：设F 是AB中点，以E为原点，EF所在直线为x轴，EC所在直线为y轴，EP所在直线为z
轴，建立空间直角坐标系，
     
由已知得E0,0,0,A 2,1,0 ,B 2,1,0 ,D0,1,0,P 0,0, 3 ，
设M 0,0,m(0m 3)，
uuuur uuur uuuur
   
则AM   2,1,m ,BD  2,2,0 ,DM 0,1,m
r
设平面BDM 的法向量为n a,b,c ，
uuur
r
 nBD 2a2b0
则r uuuur ，
nDM bmc0
r  1 
令b 1，有n    2,1, ，
 m
设直线AM 与平面BDM 所成的角，
uuuur
r
uuuur
r nAM 2
sin cos n,AM  uuuur 
所以 r
n  AM 1
3m2  3
m2
2 1
 
 1  2
103 m2 
 
 m2 
（表达式2分，不等式1分）
当且仅当m 1时取等号，
当AM 2时，直线AM 与平面BDM 所成角最大.
b2

c 6
18.解：（1）由题设得  ，
a 3

a2 b2 c2

x2 y2
解得a2 12，所以C的方程为  1
12 4
（2）由题意可设l : y kxmm2 ，设Ax ,y ,Bx ,y  ，
AB 1 1 2 2
y kxm
由  x2 y2 ，整理得  13k2 x2 6kmx3m2 120，
 1

12 4
Δ36k2m2 4  13k2 3m2 12  12  12k2 m2 4  .3m2 12 6mk
由韦达定理得x x  ,x x  ，
1 2 13k2 1 2 13k2
y 2 y 2
由k k 4k 得 1  2 4k，
PA PB AB x x
1 2
kx m2 kx m2
即 1  2 4k，
x x
1 2
所以 m2x x 2kx x 0
1 2 1 2
整理得2mkm22  4m2 k ，因为k  0，得m2 m20，
解得m  2或m1，
m 
2时，直线AB过定点P0,2
舍去；
m1时，满足Δ36  4k2 1  0，
所以直线AB过定点
0,1
.
（3）由（2）知
1
S  FF y  y 2 2|k| x x
F 1 AF 2 B 2 1 2 1 2 1 2
144k2 36 4k4 k2
2 2 k 12 2
13k2 13k2
1
4
k2
12 2
1
3
k2
1 1 1
因为k  ，所以k2  ，所以0 8，
AF 2 2 2 8 k2
1  
令t  4,t 2,2 3 ，
k2
t 1
S 12 2 12 2  
所以 F 1 AF 2 B t2 1 1 ，在t 2,2 3 上单调递减，
t
t
24 6 
所以S 的范围是 ,8 2.
F 1 AF 2 B  11 
 
19.解：（1）设 b  的公比为q，则b bq2 2q2 8,q2 4，
n 3 1解得q2
当q 2时，数列 b  为2,4,8,16,8,4,2
n
当q2时，数列 b  为2,4,8,16,8,4,2
n
（2）S c c L L c c c L L c
2k1 1 2 k k1 k2 2k1
2c c L L c c
k1 k2 2k1 k1
S C C L C C C L C
2k1 1 2 k k1 k2 2k1
 k1k 
2100k1 4 100
2
 
200k2004kk1100
 492 
4k2 49k 492 100
4
 
2
 49
4 k 2501
 
 2 
当k 24或25时，S 取得最大值2500.
2k1
另解：当该S数列恰为4，8，.96，100，96，.8,4
或0,4,8，96，100，96，8,4,0时取得最大值，
49624
所以当k 24或25时，S  21002500.
2k1 2
（3）所有可能的“对称数列”是：
①1,2,22,2m2,2m1,2m2,,22,2,1；
②1,2,22,2m2,2m1,2m1,2m2,22,2,1；
③2m1,2m2,L ,22,2,1,2,22,L ,2m2,2m1
④2m1,2m2,L ,22,2,1,1,2,22,L ,2m2,2m1
（写任意一种情况1分，四种全齐得2分）
对于①，
当m2024时，S 1222 L 22023 22024 1
2024当1500m2023时，
S 12L 2m2 2m12m2 L 22m2025
2024
2m 12m122m2025
2m 2m122m2025 1
对于②，
当m2024时，S 22024 1
2024
当1500m2023时，S 2m122m2024 1
2024
对于③，
当m2024时，S 2m 2m2024
2024
当1500m2023时，S 2m 22025m 3
2024
对于④，
当m2024时，S 2m 2m2024
2024
当1500m2023时，S 2m 22024m 2
2024
（写任意一种情况3分，四种全齐得6分，其他每个1分）