湘豫名校联考2023届高三3月第一次模拟考试理数答案(1)_2024年2月_022月合集_2023届湘豫名校联考高三3月第一次模拟考试（全科含答案）

湘 豫 名 校 联 考 #$#%年%月高三第一次模拟考试 数学!理科"参考答案 题号 ! # % & ’ ( ) * " !$ !! !# 答案 + , , - - . + . , . + , 一#选择题$本题共!#小题%每小题’分%共($分/在每小题给出的四个选项中%只 有一项是符合题目要求的/ !!+!&命题意图’本题考查集合的运算#解不等式$考查了数学运算的核心素养! &解析’因为集合"0!#"!###1##1%$$"0!#"!#1!$#$%"#$0!#"!###1##%!"#所以&! $0!#" !###1##’!"0!#"!#!’#’%"!所以"($&! $%0!#"!#!’#’%"0$!#%%!故选+! #!,!&命题意图’本题考查复数的运算#复数的几何意义$考查了数学运算#直观想象的核心素养! !1&2 $!1&2%$!12% !1&1$&3!%2 !1& &3! &解析’因为复数%0 0 0 0 1 2#其在复平面内对应的点位于第 !32 $!32%$!12% # # # %!1&)$# 四象限#所以 解得1!’&’!!所以实数&的取值范围为$1!#!%!故选,! &3!)$# %!,!&命题意图’本题考查等差数列的性质#等比数列的通项及其性质$考查了数学运算#逻辑推理的核心 素养! &解析’设等比数列!& ’ "的公比为(#因为%& ’ 是& ( 和& ) 的等差中项#所以(& ’ 0& ( 3& ) #即(& ’ 0& ’(3& ’(#! 因为& ’*$#所以(#3(1(0$#解得(0#或(01%!因为等比数列!& ’ "是递增数列#所以(0#!又因为& % 0 &#所以& !$ 0& %()0&4#)0’!#!故选,! &!-!&命题意图’本题考查函数的周期性及函数图象的对称性$考查了数学抽象#逻辑推理的核心素养! &解析’因为)$#3!%为偶函数#所以)$!3#%0)$!1#%#所以)$#%0)$#1#%!又)$#3#%3)$#1#%0$# 所以)$#3#%01)$#%!所以)$#3&%01)$#3#%0)$#%#所以函数)$#%的一个周期为&#所以)$#$#%%0 )$’$(4&1!%0)$1!%01)$!%01!!故选-! ’!-!&命题意图’本题考查相互独立事件和相互独立事件的概率乘法公式$考查了转化思想和数据分析求解 能力以及数学建模的核心素养! &解析’设该小组三人能同时进入决赛为事件"#则该小组三人能同时进入决赛即前两轮比赛三人都顺利通 % # # % # # ! 过#则*$"%0 4 4 4 4 4 0 !故选-! & % % & % % " (!.!&命题意图’本题考查圆与双曲线的综合问题$以及双曲线离心率的求法$考查了运算求解能力和数学运 算的核心素养! &解析’方法一&依题意#易得以+ ! + # 为直径的圆的方程为##3,#0-#!又由 ## ,# / 双曲线.& 1 0!$&)$#/)$%#易得双曲线.的渐近线方程为,05 #! &# /# & 当,0 & / #时#如图#设*$# $ #,$ %#则0$1# $ #1,$ %!联立+ , ,0 & / ## 解得 -##3,#0-## %#0&# %#01&# 或 所以*$&#/%#0$1
/%!又因为"$1&#$%#所以"0.# ,0/# ,01/# 数学!理科"参考答案!第!!!!!页!共"页" 书书书00/ 00/ 00/ 00/ 轴!因为"*0$#&#/%#"00$$#1/%!所以"*’"001/#01&&##所以/0#&!因为/#0-##所以’� / -#!同理#当,01 #时#亦可得’�-#!故双曲线.的离心率为10槡’!故选.! & 00/ 00/ ! 00/ 00/ 方法二$极化恒等式%&易得坐标原点2为线段*0的中点#且#*0#0#-#所以"*’"00 ($"*3"0%#1 & 00/ 00/ ! 00/ 00/ $"*1"0%#)0 $##"2##1#0*##%0
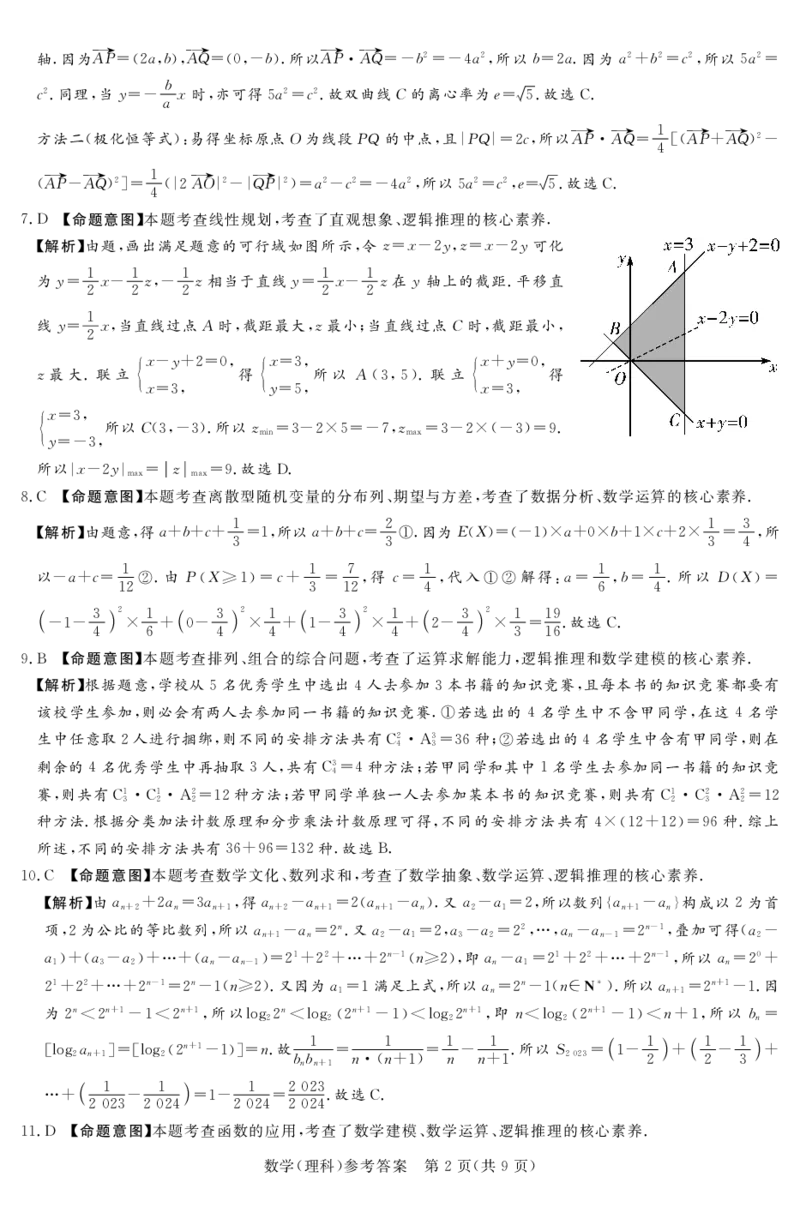
-#01&&##所以’�-##10槡’!故选./ & )!+!&命题意图’本题考查线性规划$考查了直观想象#逻辑推理的核心素养! &解析’由题#画出满足题意的可行域如图所示#令%0#1#,#%0#1#,可化 ! ! ! ! ! 为,0 #1 %#1 %相当于直线,0 #1 %在,轴上的截距!平移直 # # # # # ! 线,0 ##当直线过点"时#截距最大#%最小*当直线过点.时#截距最小# # %#1,3#0$# %#0%# %#3,0$# %最大!联立 得 所以 "$%#’%!联立 得 #0%# ,0’# #0%# %#0%# 所以.$%#1%%!所以% 0%1#4’01)#% 0%1#4$1%%0"! 627 689 ,01%# 所以##1#,#689 0 % 689 0"!故选+/ *!.!&命题意图’本题考查离散型随机变量的分布列#期望与方差$考查了数据分析#数学运算的核心素养! ! # ! % &解析’由题意#得&3/3-3 0!#所以&3/3-0 !!因为3$4%0$1!%4&3$4/3!4-3#4 0 #所 % % % & ! ! ) ! ! ! 以1&3-0 "!由*$4%!%0-3 0 #得-0 #代入!"解得&&0 #/0 !所以5$4%0 !# % !# & ( & ! %"# ! ! %"# ! ! %"# ! ! %"# ! !" 1!1 4 3 $1 4 3 !1 4 3 #1 4 0 !故选.! & ( & & & & & % !( "!,!&命题意图’本题考查排列#组合的综合问题$考查了运算求解能力$逻辑推理和数学建模的核心素养! &解析’根据题意#学校从’名优秀学生中选出&人去参加%本书籍的知识竞赛#且每本书的知识竞赛都要有 该校学生参加#则必会有两人去参加同一书籍的知识竞赛!!若选出的&名学生中不含甲同学#在这&名学 生中任意取#人进行捆绑#则不同的安排方法共有.# & ’-% % 0%(种*"若选出的&名学生中含有甲同学#则在 剩余的&名优秀学生中再抽取%人#共有.%0&种方法*若甲同学和其中!名学生去参加同一书籍的知识竞 & 赛#则共有.!’.!’-#0!#种方法*若甲同学单独一人去参加某本书的知识竞赛#则共有.!’.#’-#0!# % # # # % # 种方法/根据分类加法计数原理和分步乘法计数原理可得#不同的安排方法共有&4$!#3!#%0"(种/综上 所述#不同的安排方法共有%(3"(0!%#种/故选,/ !$!.!&命题意图’本题考查数学文化#数列求和$考查了数学抽象#数学运算#逻辑推理的核心素养! &解析’由& 3#&0%& #得& 1& 0#$& 1&%!又&1&0##所以数列!& 1&"构成以#为首 ’3# ’ ’3! ’3# ’3! ’3! ’ # ! ’3! ’ 项##为公比的等比数列#所以& 1&0#’!又&1&0##&1&0###+#&1& 0#’1!#叠加可得$&1 ’3! ’ # ! % # ’ ’1! # & ! %3$& % 1& # %3+3$& ’ 1& ’1! %0#!3##3+3#’1!$’%#%#即& ’ 1& ! 0#!3##3+3#’1!#所以& ’ 0#$3 #!3##3+3#’1!0#’1!$’%#%!又因为& ! 0!满足上式#所以& ’ 0#’1!$’""1%!所以& ’3! 0#’3!1!!因 为#’’#’3!1!’#’3!#所以:;<# #’’:;<# $#’3!1!%’:;<# #’3!#即’’:;<# $#’3!1!%’’3!#所以/ ’ 0 ! ! ! ! ! !" !! !" (:;<# & ’3! )0(:;<# $#’3!1!%)0’!故 // 0 ’’$’3!% 0 ’ 1 ’3! !所以6 #$#% 0 !1 # 3 # 1 % 3 ’’3! !! ! " ! #$#% +3 1 0!1 0 !故选.! #$#% #$#& #$#& #$#& !!!+!&命题意图’本题考查函数的应用$考查了数学建模#数学运算#逻辑推理的核心素养! 数学!理科"参考答案!第!!!!#页!共"页"! &解析’由题意得#销售收入为!$$#万元#当产量不足’$万件时#利润)$#%0!$$#17$#%1#$$01 #%3 !#$ ! (&$$" &$#1#$$*当产量不小于’$万件时#利润)$#%0!$$#17$#%1#$$0!!($1 #3 !所以利润 # , 1 ! #%3&$#1#$$#$’#’’$# !#$ ! )$#%0+ 因为当$’#’’$时#)8$#%01 $#3&$%$#1&$%#所以)$#%在 ! (&$$" &$ !!($1 #3 ##%’$! - # #($$ ! (&$$" $$#&$%上单调递增#在$&$#’$%上单调递减#则)$#%$)$&$%0 !当#%’$时#!!($1 #3 $ % # !!($1#槡#4 (&$$ 0!$$$#当且仅当#0*$时取等号!又!$$$) #($$ #所以当#0*$时#所获利润最大# # % 最大值为!$$$万元!故选+! !#!,!&命题意图’本题考查对数大小的比较及导数的应用$考查了数学抽象#逻辑推理#数学运算的核心素养! :7#$## :7#$#% $:7#$##%#1:7#$#!’:7#$#% &解析’:;<#$#! #$##1:;<#$## #$#%0 :7#$#! 1 :7#$## 0 :7#$#!’:7#$## ! !:7#$#!3:7#$#%"# &:7$#$###1!%’# !:7#$###"# 因为:7#$#!’:7#$#%’ 0 ’ 0$:7#$##%##所以 # # # #$#% :;<#$#! #$##1:;<#$## #$#%)$#所以:;<#$#! #$##):;<#$## #$#%!比较:;<#$#! #$##与 #$## 的大小#即比较 ! !3 1:7# :7#$## :7#$#! :7# # ! 与 的大小!令)$#%0 $#)$%#则)8$#%0 !令9$#%0!3 1:7##则 #$#% #$## #3! $#3!%# # ! ! ! 98$#%01 1 ’$!所以9$#%在定义域上单调递减#所以当#)=# 时#9$#%’9$=#%0!3 1#’$#所 ## # =# :7#$## :7#$#! 以)8$#%’$#所以)$#%在$=##3>%上单调递减!所以)$#$##%’)$#$#!%#即 ’ !所以 #$#% #$## :7#$## #$#% #$#% #$#% :7#$#! ’ #$## #即:;<#$#! #$##’ #$## !综上所述#:;<#$## #$#%’:;<#$#! #$##’ #$## !故选,! 二#填空题$本题共&小题%每小题’分%共#$分! !!槡!% !%! !&命题意图’本题考查向量的运算法则$考查了数学抽象#直观想象的核心素养! !% !! ! " # " &解析’因为向量!0$!#:%#"0$##:%##0!1 "#所以#0 1 # : !因为".##:)$#所以"’#0$#即 !% !%!% !* # 1 3 :#0$#解得:0%$负值舍去%!所以!0$!#%%#"0$##%%$所以!’"0!4#3%4%0!!!所以!在" !% !% !’" !! !!槡!% 方向上的投影为 0 0 ! #"# 槡!% !% !&!%或1’$只答一个不得分%!&命题意图’本题考查二项式定理$考查了数学运算的核心素养! ! !"( &解析’因为 &槡#3 的展开式中各项系数的和为$&3!%(#各二项式系数的和为#(#所以由题意得 槡% # $&3!%( 0(&0#(#所以&3!0&#或&3!01&#解得&0%#或&01’! #( !’!#$槡!’#!&命题意图’本题考查线面垂直以及三棱锥的外接球问题$考查了学生的运算求解能力和直观想 象#数学运算的核心素养! &解析’因为"$0$.0*$0#槡%#".0(#所以在2"$.中#根据余弦定理可得&".#0"$#3$.#1#"$’ 数学!理科"参考答案!第!!!!%页!共"页"$.?;@3"$.#即%(0$#槡%%#3$#槡%%#1#4$#槡%%#?;@3"$.#所以 ! ?;@3"$.01 #所以3"$.0!#$A!所以底面2"$.是顶角为!#$A的等 # 腰三角形!由题意将三棱锥*1"$.补成如图所示的直三棱柱;*61 "$.#则该直三棱柱的外接球即为三棱锥*1"$.的外接球#且直三棱柱 的外接球球心落在上,下底面外接圆圆心连线的中点上!设2"$.外接圆 的半径为<#三棱锥*1"$.外接球的半径为=#由正弦定理得##<0 ". ( !*$"# 0 0&槡%#所以<0#槡%#=#0<#3 0!#3%0!’!所以三 @273"$. 槡% # # & 棱锥*1"$.外接球的体积为>0 #=%0#$槡!’#! % !(!1!!&命题意图’本题考查直线与椭圆的位置关系$考查了直观想象#数学运算#逻辑推理的核心素养! &解析’由题意知#直线?的斜率存在且不为$和1!#设直线?的方程为,3!0@$#1#%#即,0@#1#@1!! ,,0@#1#@1!# 设A$# ! #,! %#B$# # #,# %#点A#B的坐标均不为$$#3 1 !%#联立+## 整理得$!3&@#%##1*@$#@3 3,#0!# -& !%#3!(@#3!(@0$#则!0(&@#$#@3!%#1&$!3&@#%$!(@#3!(@%01(&@)$#解得@’$!因为!)$时# #3# 0 *@$#@3!% ### 0 !(@#3!(@ #所 以@ 3@ 0 ,! 1! 3 ,# 1! 0 $,! 1!%# # 3$,# 1!%# ! 0 ! # !3&@# ! # !3&@# ! # # # ## ! # ! # !(@#3!(@ *@$#@3!% #@’ 1#$@3!%’ $@#1#@1#%#3$@#1#@1#%# #@##1#$@3!%$#3#% !3&@# !3&@# ! # # !0 ! # ! # 0 0 ## ## !(@#3!(@ ! # ! # !3&@# 1!! 三#解答题$共)$分!解答应写出文字说明#证明过程或演算步骤!第!)$#!题为 必考题%每个试题考生都必须作答!第####%题为选考题%考生根据要求作答! !一"必考题$共($分! !)!&命题意图’本题考查三角恒等变换#解三角形$考查了数学运算#逻辑推理的核心素养! ! #" &解析’$!%因为)$#%0#槡%?;@#1 ?;@#3#@27##0#槡%@27#?;@#3#@27## # ! #" 0槡%@27##3$!1?;@##%0槡%@27##1?;@##3!0#@27##1 3!#………………………………… %分 ( ! #" ! #" 所以)$"%0#@27#"1 3!0%#所以@27#"1 0!!…………………………………………… &分 ( ( # # # 所以#"1 0 3#@##@"##即"0 3@##@"#! ( # % # 又$’"’##所以"0 !…………………………………………………………………………………… ’分 % ! $#%方法一&在2"$.中#由余弦定理可得$.#0�/#3-#1#/-?;@3$".0"3&1!#4 0)# # #槡) 则$.0槡)!又点5为$.边上靠近点.的三等分点#所以$50 !………………………………… )分 % -#1/# )3&1" 槡) 又在2"$.中#?;@$0 0 0 #……………………………………………………… "分 #&- &槡) !& 数学!理科"参考答案!第!!!!&页!共"页"#* #槡) 槡) ’# 在2"$5中#由余弦定理可得"5#0$"#3$5#1#$"4$54?;@$0&3 1#4#4 4 0 # " % !& " #槡!% 所以"50 ! ………………………………………………………………………………………… !#分 % 00/ #00/ !00/ 方法二&因为点5为$.边上靠近点.的三等分点#所以"50 ".3 "$!………………………… *分 % % 00/ & 00/ ! 00/ &00/ 00/ & & ! ’# 等式两边同时平方可得#"5##0 #".##3 #"$##3 ".’"$0&3 3 4%4#4 0 # " " " " " # " ………………………………………………………………………………………………………… !$分 00/ #槡!% #槡!% 所以#"5#0 #即"50 !……………………………………………………………………… !#分 % % !*!&命题意图’本题考查统计#独立性检验$考查了数据分析#数学运算#逻辑推理的核心素养! &解析’$!%因为$$!$!$3$!$%$%4!$0$!&’$!’#$!&3$!$&’4!$0$!*’)$!’# 所以竞赛成绩的中位数在()$#*$%内!……………………………………………………………………… %分 设竞赛成绩的中位数为C#则$C1)$%4$!$&’3$!&0$!’#解得C4)## 所以估计这!$$名学生的竞赛成绩的中位数为)#!……………………………………………………… ’分 $#%由$!%知#在抽取的!$$名学生中# 竞赛成绩为-优秀.的有&!$$4$$!&’3$!!$3$!$’%0!$$4$!(0($人# ……………………………… (分 由此可得完整的#4#列联表& 优秀 非优秀 合计 男 #$ %$ ’$ 女 &$ !$ ’$ 合计 ($ &$ !$$ ………………………………………………………………………………………………………………… *分 !$$4$#$4!$1&$4%$%# !$$ 因为D#的观测值@0 0 4!(!(())(!(%’#……………………………… !!分 ($4&$4’$4’$ ( 所以有""B的把握认为-竞赛成绩是否优秀与性别有关.! …………………………………………… !#分 !"!&命题意图’本题考查了空间向量中的线面角以及点的存在性问题$考查了学生的逻辑推理#运算求解能力 和直观想象#数学运算的核心素养! &解析’方法一&$!%因为"55$.#$.."$#所以"5."$! ! 又因为"$0"50 $.#$50槡## # 所以"$0"50!#$.0#!…………………………………………………… #分 因为*".平面"$.5#"$6平面"$.5#"56平面"$.5# 所以*"."$#*"."5!又*50槡’#所以*"0槡*5#1"5#0#! 以"为坐标原点#以"$#"5#"*所在直线分别为#轴,,轴,%轴#建立如图所 示的空间直角坐标系# 则$$!#$#$%#.$!###$%#5$$#!#$%#*$$#$##%!…………………………………………………………… &分 00/ 00/ 00/ 所以*.0$!###1#%#$50$1!#!#$%#$*0$1!#$##%! 设平面*$5的法向量为%0$##,#%%# 数学!理科"参考答案!第!!!!’页!共"页"%$ 00/ 5’%0$# %1#3,0$# ,,0## 则 $ 00/ *’%0$# 即 1#3#%0$# 得+ -%0 ! # #! 令#0##可得平面*$5的一个法向量为%0$####!%! 00/ 00/ *.’% & 设直线*.与平面*$5所成的角为"#则@27"0#?;@/*.#%0#0 00/ 0 ! *. ’#%# " & 所以直线*.与平面*$5所成角的正弦值为 !………………………………………………………… (分 " $#%不存在点A#理由如下& 假设存在满足条件的点A$如图%! 00/ 00/ 可设$A0#$*0$1##$###%##"($#!)#所以A$!1##$###%! 00/ 所以.A0$1##1####%! …………………………………………………… *分 00/ 1# 1# 又由$!%知%0$####!%为平面*$5的一个法向量#所以.A5%#即 0 0 # # ## #无解! ! 所以线段*$上不存在满足条件的点A!………………………………… !#分 方法二$几何推理法%& $!%如图#连接".!因为"55$.#$.."$#所以"5."$! 因为"$0"50 ! $.#$50!槡##所以"$0"50!#$.0#! # 因为$.."$#所以".0槡"$#3$.#0槡’!……………………………… #分 因为*".平面"$.5#"$6平面"$.5#".6平面"$.5#"56平面"$.5# 所以*"."$#*".".#*"."5! 因为*"0槡*5#1"5#0##所以*.0!槡".#3*"#0%#*$0槡*"#3"$#0 槡’! 所以6 0 ! 4!槡#4槡 ! $!槡’%# 1 !!槡#"# 0 % #6 0 ! 4$.4"$0 ! 4#4!0!! …………… &分 2*$5 # # # 2$.5 # # 设点.到平面*$5的距离为E# ! ! & 由> 0> #得 4*"46 0 4E46 #解得E0 ! *1$5. .1*$5 % 2$.5 % 2*$5 % E & 设直线*.与平面*$5所成的角为"#则@27"0 0 ! *. " & 所以直线*.与平面*$5所成角的正弦值为 !………………………………………………………… (分 " $#%不存在点A#理由如下& 假设存在满足条件的点A# 由.A.平面*$5#*$6平面*$5#$56平面*$5#得.A.*$#且.A.$5! 因为*".平面"$.5#$.6平面"$.5#所以*".$.! ……………………………………………… *分 因为$.."$#且*"("$0"#*"6平面*"$#"$6平面*"$# 所以$..平面*"$!又*$6平面*"$#所以$..*$!……………………………………………… !$分 若存在满足条件的点A#则点A必与点$重合! 又$.与$5不垂直#所以线段*$上不存在满足条件的点A!………………………………………… !#分 数学!理科"参考答案!第!!!!(页!共"页"#$!&命题意图’本题考查直线与抛物线的位置关系及其应用$考查了直观想象#数学运算#逻辑推理的核心素 养! 7 7 &解析’$!%设点*的坐标为$# $ #,$ %#由抛物线定义可知##*+#0# $ 3 # % # # 7 故 0!#解得70##所以抛物线.的标准方程为,#0&#!……………………………………………… #分 # $#%由$!%易知+$!#$%#设"$# ! #,! %#$$# # #,# %#A$# % #,% %# 若"$.#轴#由A+."$#得A$$#$%#"$!##%#$$!#1#%或"$!#1#%或$$!##%# 此时不满足"A.$A#所以不满足题意* ………………………………………………………………… %分 ! 设直线"$的方程为#0C,3!$C*$%#直线A+的方程为#01 ,3!$C*$%#如图所示# C 将#0C,3!代入抛物线方程得,#1&C,1&0$#所以,! 3,# 0&C# ,!,# 01&! ! & & 将#01 C ,3!代入抛物线方程得,#3 C ,1&0$#所以,# % 3 C ,% 1&0 $!!……………………………………………………………………… ’分 直线"A的斜率为 ,% 1,!0 ,% 1,!0 & #同理$A的斜率为 & ! # % 1# ! ,# %1 ,# ! ,% 3,! ,% 3,# & & & & 因为"A.$A#所以 ’ 01!# ,% 3,! ,% 3,# 所以,# % 3$,! 3,# %,% 3,!,# 01!(#即,# % 3&C,% 3!#0$"!…………………………………………… )分 &C 由!"解得,% 0 !1C# #将其代入!可得#&C#3&$!1C#%1$!1C#%#0$# ,C0槡%# ,C01槡%# 所以+ 或+ …………………………………………………………………………… *分 -,% 01#槡%# -,% 0#槡%! ,C0槡%# 当+ 时#直线"$的方程为#0槡%,3!#A$%#1#槡%%##A+#0&!…………………………… "分 -,% 01#槡% 因为,! #,# 满足,#1&槡%,1&0$#所以,! 3,# 0&槡%#,!,# 01&! 所以#"$#0槡!3C##,! 1,##0#槡$,! 3,# %#1&,!,# 0!(# ! ! 所以6 2"$A 0 # 4#"$#4#A+#0 # 4!(4&0%#! …………………………………………………… !$分 ,C01槡%# 同理可得#当+ 时#直线"$的方程为#01槡%,3!#2"$A的面积也为%#!……………… !!分 -,% 0#槡% 所以2"$A的面积为%#!………………………………………………………………………………… !#分 #!!&命题意图’本题考查利用导数研究函数图象的切线方程及函数的单调性与最值$不等式的证明$考查了转 化思想#分类讨论思想#逻辑推理#数学运算的核心素养! &解析’$!%因为)$#%0#:7#3#3!$#)$%#所以)8$#%0:7#3#! 所以)8$!%0#! 又因为)$!%0##……………………………………………………………………………………………… #分 所以函数)$#%的图象在点$!#)$!%%处的切线方程为,1#0#$#1!%# 即##1,0$!………………………………………………………………………………………………… &分 $#%方法一& 数学!理科"参考答案!第!!!!)页!共"页"! =# =# ! 证明&要证)$#%’=##即证#:7#3#3!’=##即证:7#3!3 ’ #即证 1:7#1 1!)$!…… (分 # # # # =# ! $#1!%=# ! ! $#1!%$=#1!% 令9$#%0 1:7#1 1!$#)$%#则98$#%0 1 3 0 ! # # ## # ## ## 由98$#%0$#可得#0!! …………………………………………………………………………………… *分 因为当#)$时#=#1!)$# 所以当$’#’!时#98$#%’$#9$#%单调递减* 当#)!时#98$#%)$#9$#%单调递增!…………………………………………………………………… !$分 所以9$#% 627 09$!%0=1!1!0=1#)$! 所以9$#%)$#结论得证!…………………………………………………………………………………… !#分 方法二& 证明&因为)$#%0#:7#3#3!# 所以要证)$#%’=##即证#:7#3#3!’=#! 即证#:7#1=#3#3!’$! ………………………………………………………………………………… ’分 设$ $#%0#:7#1=#3#3!$#)$%# 则$8$#%0:7#3!1=#3!0:7#1=#3#!………………………………………………………………… (分 ! 令E$#%0:7#1=#3#$#)$%#则E8$#%0 1=#! # 易知函数E8$#%在$$#3>%上单调递减# !!" 又E8 0#1槡=)$#E8$!%0!1=’$# # !! " ! ! 故存在唯一的# $" # #! #使得E8$# $ %0$#即 # 1=#$0$#即 # 0=#$!……………………………… *分 $ $ 等式两边同时取对数得1:7#0##即:7#01#! $ $ $ $ 当#"$$## $ %时#E8$#%)$#E$#%单调递增* 当#"$# $ #3>%时#E8$#%’$#E$#%单调递减 ! ! $#1!%# 所以E$#% 689 0E$# $ %0:7# $ 1=#$3#01# $ 1 # 3#01 $ # ’$#即$8$#%’$! $ $ 所以$ $#%在$$#3>%上单调递减!………………………………………………………………………… !$分 因为当#/$3时##:7#3#0#$:7#3!%’$#!1=#’$#所以函数$ $#%’$! 所以)$#%’=#成立! ……………………………………………………………………………………… !#分 !二"选考题$共!$分!请考生在####%题中任选一题作答%如果多做%则按所做的 第一题计分! ##!&解析’本题考查直线的极坐标方程与直角坐标方程的互化$圆的参数方程问题$考查了学生的直观想象能 力$数据分析求解能力和数学运算的核心素养! $!%因为圆.的圆心坐标为$1##1#%#且过原点2#所以圆.的半径<0槡$1#%#3$1#%#0#槡#! 所以圆.的直角坐标方程为$#3#%#3$,3#%#0*! ,#01#3#槡#?;@"# 由此可以得到圆.的参数方程为+ $"为参数%!……………………………………… %分 -,01#3#槡#@27" %#0%?;@"# 因为 将其代入直线?的极坐标方程% $?;@"3@27"%01!中# ,0%@27"# 可得#3,01!#即直线?的直角坐标方程为#3,3!0$!……………………………………………… ’分 数学!理科"参考答案!第!!!!*页!共"页"$#%由$!%知直线?,3!0$# 圆.的圆心坐标为$1##1#%#半径为#槡#! #1#1#3!# %槡# 因为圆心$1##1#%到直线?的距离F0 0 #…………………………………………… *分 槡# # 所以#"$#0#槡*1 " 0槡!&! # )槡# 又点*在圆.上运动#所以点*到直线"$的最大距离为F3<0 ! # ! )槡# )槡) 所以2*"$面积的最大值为 4槡!&4 0 !…………………………………………………… !$分 # # # #%!&命题意图’本题考查不等式$考查了数学运算#逻辑推理的核心素养! &解析’$!%因为:)$# 1$#1:%3#$#3%%0#3:3(##$1%# , 所以)$#%0##1:#1###3%#0+1$#1:%1#$#3%%01%#1(3:#1%’#’:# -$#1:%1#$#3%%01#1(1:##%:# #3:3(##$1%# , 即)$#%0+1%#3:1(#1%’#’:#………………………………………………………………………… %分 -1#1:1(##%:! 因为)$#%在$1>#1%)上单调递增#在$1%#:%#(:#3>%上单调递减# 所以)$#% 689 0)$1%%01%3:3(0’#所以:0#!……………………………………………………… ’分 $#%由$!%知:0##则&3#/0#!因为&)$#/)$# # ! ! !# !" !! &/ & " 所以 3 0 4$&3#/% 3 0 #3 3 3# & / # & / # & / 0#3 !!&/ 3 &" %#3 ! 4#槡&/ ’ & 0#3#0&#…………………………………………………… *分 # & / # & / &/ & 当且仅当 0 #即&0#/时#等号成立! & / ! # ! 又&3#/0##所以当&0!#/0 时# 3 取得最小值&! …………………………………………… !$分 # & / 数学!理科"参考答案!第!!!!"页!共"页"