文档内容
五年(2019-2023)年高考真题分项汇编
专题 04 导数及应用(解答题)
函数导数应用是高考必考知识点 ,解答题主要是压轴题的形式出现,常考题型如图所示:
考点 01 利用导数求函数单调性,求参数
一、解答题
1.(2023·全国乙卷)已知函数 .
(1)当 时,求曲线 在点 处的切线方程;
(2)是否存在a,b,使得曲线 关于直线 对称,若存在,求a,b的值,若不存在,说明理由.
(3)若 在 存在极值,求a的取值范围.
【答案】(1) ;
(2)存在 满足题意,理由见解析.
(3) .
【分析】(1)由题意首先求得导函数的解析式,然后由导数的几何意义确定切线的斜率和切点坐标,最后求
解切线方程即可;
(2)首先求得函数的定义域,由函数的定义域可确定实数 的值,进一步结合函数的对称性利用特殊值法可
得关于实数 的方程,解方程可得实数 的值,最后检验所得的 是否正确即可;
1(3)原问题等价于导函数有变号的零点,据此构造新函数 ,然后对函数求导,
利用切线放缩研究导函数的性质,分类讨论 , 和 三中情况即可求得实数 的取值范围.
【详解】(1)当 时, ,
则 ,
据此可得 ,
函数在 处的切线方程为 ,
即 .
(2)由函数的解析式可得 ,
函数的定义域满足 ,即函数的定义域为 ,
定义域关于直线 对称,由题意可得 ,
由对称性可知 ,
取 可得 ,
即 ,则 ,解得 ,
经检验 满足题意,故 .
即存在 满足题意.
(3)由函数的解析式可得 ,
由 在区间 存在极值点,则 在区间 上存在变号零点;
令 ,
则 ,
令 ,
在区间 存在极值点,等价于 在区间 上存在变号零点,
2当 时, , 在区间 上单调递减,
此时 , 在区间 上无零点,不合题意;
当 , 时,由于 ,所以 在区间 上单调递增,
所以 , 在区间 上单调递增, ,
所以 在区间 上无零点,不符合题意;
当 时,由 可得 ,
当 时, , 单调递减,
当 时, , 单调递增,
故 的最小值为 ,
令 ,则 ,
函数 在定义域内单调递增, ,
据此可得 恒成立,
则 ,
令 ,则 ,
当 时, 单调递增,
当 时, 单调递减,
故 ,即 (取等条件为 ),
所以 ,
,且注意到 ,
根据零点存在性定理可知: 在区间 上存在唯一零点 .
当 时, , 单调减,
当 时, , 单调递增,
3所以 .
令 ,则 ,
则函数 在 上单调递增,在 上单调递减,
所以 ,所以 ,
所以
,
所以函数 在区间 上存在变号零点,符合题意.
综合上面可知:实数 得取值范围是 .
【点睛】(1)求切线方程的核心是利用导函数求切线的斜率,求函数的导数要准确地把函数拆分成基本初等
函数的和、差、积、商,再利用运算法则求导,合函数求导,应由外到内逐层求导,必要时要进行换元.
(2)根据函数的极值(点)求参数的两个要领:①列式:根据极值点处导数为0和极值这两个条件列方程组,利
用待定系数法求解;②验证:求解后验证根的合理性.本题中第二问利用对称性求参数值之后也需要进行验证.
2.(2022·全国乙卷)已知函数
(1)当 时,求曲线 在点 处的切线方程;
(2)若 在区间 各恰有一个零点,求a的取值范围.
【答案】(1)
(2)
【分析】(1)先算出切点,再求导算出斜率即可
(2)求导,对 分类讨论,对 分 两部分研究
【详解】(1) 的定义域为
4当 时, ,所以切点为 ,所以切线斜率为2
所以曲线 在点 处的切线方程为
(2)
设
若 ,当 ,即
所以 在 上单调递增,
故 在 上没有零点,不合题意
若 ,当 ,则
所以 在 上单调递增所以 ,即
所以 在 上单调递增,
故 在 上没有零点,不合题意
若
(1)当 ,则 ,所以 在 上单调递增
所以存在 ,使得 ,即
当 单调递减
当 单调递增
所以
当 ,
令 则
所以 在 上单调递增,在 上单调递减,所以 ,
又 , ,
所以 在 上有唯一零点
又 没有零点,即 在 上有唯一零点
(2)当
5设
所以 在 单调递增
所以存在 ,使得
当 单调递减
当 单调递增,
又
所以存在 ,使得 ,即
当 单调递增,当 单调递减,
当 , ,
又 ,
而 ,所以当
所以 在 上有唯一零点, 上无零点
即 在 上有唯一零点
所以 ,符合题意
所以若 在区间 各恰有一个零点,求 的取值范围为
3.(2021·全国甲卷)已知 且 ,函数 .
(1)当 时,求 的单调区间;
(2)若曲线 与直线 有且仅有两个交点,求a的取值范围.
【答案】(1) 上单调递增; 上单调递减;(2) .
【分析】(1)求得函数的导函数,利用导函数的正负与函数的单调性的关系即可得到函数的单调性;
6(2)方法一:利用指数对数的运算法则,可以将曲线 与直线 有且仅有两个交点等价转化为
方程 有两个不同的实数根,即曲线 与直线 有两个交点,利用导函数研究 的
单调性,并结合 的正负,零点和极限值分析 的图象,进而得到 ,发现这正好是
,然后根据 的图象和单调性得到 的取值范围.
【详解】(1)当 时, ,
令 得 ,当 时, ,当 时, ,
∴函数 在 上单调递增; 上单调递减;
(2)[方法一]【最优解】:分离参数
,设函数 ,
则 ,令 ,得 ,
在 内 , 单调递增;
在 上 , 单调递减;
,
又 ,当 趋近于 时, 趋近于0,
所以曲线 与直线 有且仅有两个交点,即曲线 与直线 有两个交点的充分必要
条件是 ,这即是 ,
所以 的取值范围是 .
[方法二]:构造差函数
由 与直线 有且仅有两个交点知 ,即 在区间 内有两个解,取对数得方程
在区间 内有两个解.
构造函数 ,求导数得 .
当 时, 在区间 内单调递增,所以, 在
内最多只有一个零点,不符合题意;
7当 时, ,令 得 ,当 时, ;当 时, ;
所以,函数 的递增区间为 ,递减区间为 .
由于 ,
当 时,有 ,即 ,由函数 在 内有两个零点知
,所以 ,即 .
构造函数 ,则 ,所以 的递减区间为 ,递增区间为 ,所以
,当且仅当 时取等号,故 的解为 且 .
所以,实数a的取值范围为 .
[方法三]分离法:一曲一直
曲线 与 有且仅有两个交点等价为 在区间 内有两个不相同的解.
因为 ,所以两边取对数得 ,即 ,问题等价为 与 有且
仅有两个交点.
①当 时, 与 只有一个交点,不符合题意.
②当 时,取 上一点 在点 的切线方程为
,即 .
当 与 为同一直线时有 得
直线 的斜率满足: 时, 与 有且仅有两个交点.
记 ,令 ,有 . 在区间 内单调递增;
在区间 内单调递减; 时, 最大值为 ,所当 且 时
有 .
综上所述,实数a的取值范围为 .
[方法四]:直接法
8.
因为 ,由 得 .
当 时, 在区间 内单调递减,不满足题意;
当 时, ,由 得 在区间 内单调递增,由 得
在区间 内单调递减.
因为 ,且 ,所以 ,即 ,即
,两边取对数,得 ,即 .
令 ,则 ,令 ,则 ,所以 在区间 内单调递增,在区间
内单调递减,所以 ,所以 ,则 的解为 ,所以 ,即 .
故实数a的范围为 .]
4.(2021·天津·统考高考真题)已知 ,函数 .
(I)求曲线 在点 处的切线方程:
(II)证明 存在唯一的极值点
(III)若存在a,使得 对任意 成立,求实数b的取值范围.
【答案】(I) ;(II)证明见解析;(III)
【分析】(I)求出 在 处的导数,即切线斜率,求出 ,即可求出切线方程;
(II)令 ,可得 ,则可化为证明 与 仅有一个交点,利用导数求出 的
变化情况,数形结合即可求解;
(III)令 ,题目等价于存在 ,使得 ,即 ,利用导
数即可求出 的最小值.
【详解】(I) ,则 ,
又 ,则切线方程为 ;
(II)令 ,则 ,
令 ,则 ,
9当 时, , 单调递减;当 时, , 单调递增,
当 时, , ,当 时, ,画出 大致图像如下:
所以当 时, 与 仅有一个交点,令 ,则 ,且 ,
当 时, ,则 , 单调递增,
当 时, ,则 , 单调递减,
为 的极大值点,故 存在唯一的极值点;
(III)由(II)知 ,此时 ,
所以 ,
令 ,
若存在a,使得 对任意 成立,等价于存在 ,使得 ,即 ,
, ,
当 时, , 单调递减,当 时, , 单调递增,
所以 ,故 ,
所以实数b的取值范围 .
【点睛】关键点睛:第二问解题的关键是转化为证明 与 仅有一个交点;第三问解题的关键是
转化为存在 ,使得 ,即 .
5.(2020年全国高考Ⅰ卷)已知函数 .
(1)当a=1时,讨论f(x)的单调性;
(2)当x≥0时,f(x)≥ x3+1,求a的取值范围.
【答案】(1)当 时, 单调递减,当 时, 单调递增.
(2)
10【分析】(1)由题意首先对函数二次求导,然后确定导函数的符号,最后确定原函数的单调性即可.
(2)方法一:首先讨论x=0的情况,然后分离参数,构造新函数,结合导函数研究构造所得的函数的最大值
即可确定实数a的取值范围.
【详解】(1)当 时, , ,
由于 ,故 单调递增,注意到 ,故:
当 时, 单调递减,
当 时, 单调递增.
(2) [方法一]【最优解】:分离参数
由 得, ,其中 ,
①.当x=0时,不等式为: ,显然成立,符合题意;
②.当 时,分离参数a得, ,
记 , ,
令 ,
则 , ,
故 单调递增, ,
故函数 单调递增, ,
由 可得: 恒成立,
故当 时, , 单调递增;
当 时, , 单调递减;
因此, ,
综上可得,实数a的取值范围是 .
[方法二]:特值探路
当 时, 恒成立 .
11只需证当 时, 恒成立.
当 时, .
只需证明 ⑤式成立.
⑤式 ,
令 ,
则 ,
所以当 时, 单调递减;
当 单调递增;
当 单调递减.
从而 ,即 ,⑤式成立.
所以当 时, 恒成立.
综上 .
[方法三]:指数集中
当 时, 恒成立 ,
记 ,
,
①.当 即 时, ,则当 时, , 单调递增,又 ,
所以当 时, ,不合题意;
②.若 即 时,则当 时, , 单调递减,当
时, , 单调递增,又 ,
12所以若满足 ,只需 ,即 ,所以当 时,
成立;
③当 即 时, ,又由②可知 时,
成立,所以 时, 恒成立,
所以 时,满足题意.
综上, .
6.(2020·江苏·统考高考真题)已知关于x的函数 与 在区间D上恒
有 .
(1)若 ,求h(x)的表达式;
(2)若 ,求k的取值范围;
(3)若 求证:
.
【答案】(1) ;(2) ;(3)证明详见解析
【分析】(1)方法一:根据一元二次不等式恒成立问题的解法,即可求得 的表达式;
(2)方法一:先由 ,求得 的一个取值范围,再由 ,求得 的另一个取值
范围,从而求得 的取值范围.
(3)方法一:根据题意可得两个含参数 的一元二次不等式在区间 上恒成立,再结合放
缩,即可利用导数证得不等式成立.
【详解】(1)[方法一]:判别式法
由 可得 在R上恒成立,
即 和 ,
从而有 即 ,
所以 ,
因此, .所以 .
[方法二]【最优解】:特值+判别式法
由题设有 对任意的 恒成立.
13令 ,则 ,所以 .
因此 即 对任意的 恒成立,
所以 ,因此 .
故 .
(2)[方法一]
令 , .
又 .
若 ,则 在 上递增,在 上递减,则 ,即 ,不符合题意.
当 时, ,符合题意.
当 时, 在 上递减,在 上递增,则 ,
即 ,符合题意.
综上所述, .
由
当 ,即 时, 在 为增函数,
因为 ,
故存在 ,使 ,不符合题意.
当 ,即 时, ,符合题意.
当 ,即 时,则需 ,解得 .
综上所述, 的取值范围是 .
[方法二]【最优解】:特值辅助法
由已知得 在 内恒成立;
由已知得 ,
令 ,得 ,∴ (*),
令 , ,当 时, , 单调递减;当 时,
, 单调递增,∴ ,∴当 时 在 内恒成立;
由 在 内恒成立,由(*)知 ,∴
14,∴ ,解得 .
∴ 的取值范围是 .
(3)[方法一]:判别式+导数法
因为 对任意 恒成立,
① 对任意 恒成立,
等价于 对任意 恒成立.
故 对任意 恒成立.
令 ,
当 , ,
此时 ,
当 , ,
但 对任意的 恒成立.
等价于 对任意的 恒成立.
的两根为 ,
则 ,
所以 .
令 ,构造函数 , ,
所以 时, , 递减, .
所以 ,即 .
[方法二]:判别式法
由 ,从而对任意的 有 恒成立,等价于对任意的
①,恒成立.
(事实上,直线 为函数 的图像在 处的切线)
同理 对任意的 恒成立,即等价于对任意的
恒成立. ②
当 时,将①式看作一元二次方程,进而有 ,①式的解为 或 (不妨设
15);
当 时, ,从而 或 ,又 ,从而 成立;
当 时,由①式得 或 ,又 ,所以
.
当 时,将②式看作一元二次方程,进而有 .
由 ,得 ,此时②式的解为 不妨设 ,从而
.
综上所述, .
[方法三]【最优解】:反证法
假设存在 ,使得满足条件的m,n有 .
因为 ,所以 .
因为 ,所以 .
因为 对恒成立,所以有
.则有
, ③
, ④
解得 .
由③+④并化简得, .
因为 在区间 上递增,且 ,
所以, .
由 对 恒成立,即有 ⑤
对 恒成立,将⑤式看作一元二次方程,进而有
.
设 ,则 ,
所以 在区间 上递减,所以 ,即 .
设不等式⑤的解集为 ,则 ,这与假设矛盾.从而 .
由 均为偶函数.同样可证 时, 也成立.
16综上所述, .
7.(2019年全国高考Ⅱ卷)已知函数 .
(1)讨论f(x)的单调性,并证明f(x)有且仅有两个零点;
(2)设x 是f(x)的一个零点,证明曲线y=ln x 在点A(x,ln x )处的切线也是曲线 的切线.
0 0 0
【答案】(1)函数 在 和 上是单调增函数,证明见解析;
(2)证明见解析.
【分析】(1)对函数 求导,结合定义域,判断函数的单调性;
(2)先求出曲线 在 处的切线 ,然后求出当曲线 切线的斜率与 斜率相等时,证
明曲线 切线 在纵轴上的截距与 在纵轴的截距相等即可.
【详解】(1)函数 的定义域为 ,
,因为函数 的定义域为 ,所以 ,因此函数
在 和 上是单调增函数;
当 ,时, ,而 ,显然当 ,函数 有零点,而函
数 在 上单调递增,故当 时,函数 有唯一的零点;
当 时, ,
因为 ,所以函数 在 必有一零点,而函数 在 上是单调递增,故当
时,函数 有唯一的零点
综上所述,函数 的定义域 内有2个零点;
(2)[方法一]【最优解:分别求得两条方程,比较常数项说明切线重合】
设 在点 处的斜率为 .
切线 的方程为 ,即 .
由 ,得 .
所以曲线 上斜率为 的切线的切点为 .
切线 的方程为 ,即 .
17由于 ,故曲线y=lnx在点A(x,lnx)处的切线也是曲线 的切线.
0 0
[方法二]【利用切线的斜率相等进行证明】
由题设知 ,即 ,曲线 在点 处的切线l的方程为 .
设在曲线 上取一点 ,若其在点B处的斜率与直线l的斜率相等,
则有 ,即 ,故 .
将点B的坐标代入直线l的方程 中,
,整理得 ,上式显然成立.
则直线l过点B,即曲线 在点 处的切线也是曲线 的切线.
[方法三]【利用不同的方法计算斜率证明切线重合】
因为 ,所以由 ,设切点坐标为 ,解得 .
因此,曲线 在点 处切线的斜率也是 .
因为 ,所以 ,
因此,曲线 在点 处的切线也是曲线 的切线.
[方法四]【构造函数讨论单调性证明切线重合】
因为 ,
所以曲线 在点 处的切线方程是 .
构造函数 ,由 得 .
因为当 时, ;
当 时, ,所以 .
因此,函数 只有一个零点 .
所以曲线 与曲线 在点 处的切线 只有一个交点 .
18又 ,因此,曲线 与直线 相切于 ,
即曲线 在点 处的切线也是曲线 的切线.
【整体点评】(2)方法一:分别求得两条切线方程比较切线方程的形式是最直接思路;
方法二:考查切线斜率相等时证明切线重合的必要思路;
方法三:利用不同的方法计算切线方程是证明切线重合的有效方法;
方法四:构造函数进行证明体现了等价转化的数学思想.
8.(2019年全国高考Ⅲ卷)已知函数 .
(1)讨论 的单调性;
(2)是否存在 ,使得 在区间 的最小值为 且最大值为1?若存在,求出 的所有值;若不
存在,说明理由.
【答案】(1)见详解;(2) 或 .
【分析】(1)先求 的导数,再根据 的范围分情况讨论函数单调性;(2) 根据 的各种范围,利用函数单
调性进行最大值和最小值的判断,最终得出 , 的值.
【详解】(1)对 求导得 .所以有
当 时, 区间上单调递增, 区间上单调递减, 区间上单调递增;
当 时, 区间上单调递增;
当 时, 区间上单调递增, 区间上单调递减, 区间上单调递增.
(2)若 在区间 有最大值1和最小值-1,所以
若 , 区间上单调递增, 区间上单调递减, 区间上单调递增;
此时在区间 上单调递增,所以 , 代入解得 , ,与 矛盾,所以 不成
立.
若 , 区间上单调递增;在区间 .所以 , 代入解得 .
若 , 区间上单调递增, 区间上单调递减, 区间上单调递增.
即 在区间 单调递减,在区间 单调递增,所以区间 上最小值为
而 ,故所以区间 上最大值为 .
19即 相减得 ,即 ,又因为 ,所以无解.
若 , 区间上单调递增, 区间上单调递减, 区间上单调递增.
即 在区间 单调递减,在区间 单调递增,所以区间 上最小值为
而 ,故所以区间 上最大值为 .
即 相减得 ,解得 ,又因为 ,所以无解.
若 , 区间上单调递增, 区间上单调递减, 区间上单调递增.
所以有 区间 上单调递减,所以区间 上最大值为 ,最小值为
即 解得 .
综上得 或 .
【点睛】这是一道常规的函数导数不等式和综合题,题目难度比往年降低了不少.考查的函数单调性,最
大值最小值这种基本概念的计算.思考量不大,由计算量补充.
考点 02 恒成立问题
一、解答题
1.(2023 全国新高考Ⅰ卷)已知函数 .
(1)讨论 的单调性;
(2)证明:当 时, .
【答案】(1)答案见解析
(2)证明见解析
【分析】(1)先求导,再分类讨论 与 两种情况,结合导数与函数单调性的关系即可得解;
(2)方法一:结合(1)中结论,将问题转化为 的恒成立问题,构造函数
20,利用导数证得 即可.
方法二:构造函数 ,证得 ,从而得到 ,进而将问题转化为
的恒成立问题,由此得证.
【详解】(1)因为 ,定义域为 ,所以 ,
当 时,由于 ,则 ,故 恒成立,
所以 在 上单调递减;
当 时,令 ,解得 ,
当 时, ,则 在 上单调递减;
当 时, ,则 在 上单调递增;
综上:当 时, 在 上单调递减;
当 时, 在 上单调递减, 在 上单调递增.
(2)方法一:
由(1)得, ,
要证 ,即证 ,即证 恒成立,
令 ,则 ,
令 ,则 ;令 ,则 ;
所以 在 上单调递减,在 上单调递增,
所以 ,则 恒成立,
所以当 时, 恒成立,证毕.
方法二:
令 ,则 ,
由于 在 上单调递增,所以 在 上单调递增,
又 ,
所以当 时, ;当 时, ;
21所以 在 上单调递减,在 上单调递增,
故 ,则 ,当且仅当 时,等号成立,
因为 ,
当且仅当 ,即 时,等号成立,
所以要证 ,即证 ,即证 ,
令 ,则 ,
令 ,则 ;令 ,则 ;
所以 在 上单调递减,在 上单调递增,
所以 ,则 恒成立,
所以当 时, 恒成立,证毕.
2.(2022·北京·统考高考真题)已知函数 .
(1)求曲线 在点 处的切线方程;
(2)设 ,讨论函数 在 上的单调性;
(3)证明:对任意的 ,有 .
【答案】(1)
(2) 在 上单调递增.
(3)证明见解析
【分析】(1)先求出切点坐标,在由导数求得切线斜率,即得切线方程;
(2)在求一次导数无法判断的情况下,构造新的函数,再求一次导数,问题即得解;
(3)令 , ,即证 ,由第二问结论可知 在[0,+∞)上单调递增,
即得证.
【详解】(1)解:因为 ,所以 ,
即切点坐标为 ,
又 ,
22∴切线斜率
∴切线方程为:
(2)解:因为 ,
所以 ,
令 ,
则 ,
∴ 在 上单调递增,
∴
∴ 在 上恒成立,
∴ 在 上单调递增.
(3)解:原不等式等价于 ,
令 , ,
即证 ,
∵ ,
,
由(2)知 在 上单调递增,
∴ ,
∴
∴ 在 上单调递增,又因为 ,
∴ ,所以命题得证.
3.(2021·全国乙卷)设函数 ,已知 是函数 的极值点.
(1)求a;
(2)设函数 .证明: .
【答案】(1) ;(2)证明见详解
【分析】(1)由题意求出 ,由极值点处导数为0即可求解出参数 ;
23(2)由(1)得 , 且 ,分类讨论 和 ,可等价转化为要证
,即证 在 和 上恒成立,结合导数和换元法即可求解
【详解】(1)由 , ,
又 是函数 的极值点,所以 ,解得 ;
(2)[方法一]:转化为有分母的函数
由(Ⅰ)知, ,其定义域为 .
要证 ,即证 ,即证 .
(ⅰ)当 时, , ,即证 .令 ,因为
,所以 在区间 内为增函数,所以 .
(ⅱ)当 时, , ,即证 ,由(ⅰ)分析知 在区间
内为减函数,所以 .
综合(ⅰ)(ⅱ)有 .
[方法二] 【最优解】:转化为无分母函数
由(1)得 , , 且 ,
当 时,要证 , , ,即证
,化简得 ;
同理,当 时,要证 , , ,即证
,化简得 ;
令 ,再令 ,则 , ,
令 , ,
当 时, , 单减,故 ;
当 时, , 单增,故 ;
综上所述, 在 恒成立.
24[方法三] :利用导数不等式中的常见结论证明
令 ,因为 ,所以 在区间 内是增函数,在区间 内是减
函数,所以 ,即 (当且仅当 时取等号).故当 且 时, 且
, ,即 ,所以 .
(ⅰ)当 时, ,所以 ,即 ,所以 .
(ⅱ)当 时, ,同理可证得 .
综合(ⅰ)(ⅱ)得,当 且 时, ,即 .
【整体点评】(2)方法一利用不等式的性质分类转化分式不等式:当 时,转化为证明
,当 时,转化为证明 ,然后构造函数,利用导数研究单调性,进
而证得;方法二利用不等式的性质分类讨论分别转化为整式不等式:当 时, 成
立和当 时, 成立,然后换元构造,利用导数研究单调性进而证得,通性通法,
运算简洁,为最优解;方法三先构造函数 ,利用导数分析单调性,证得常见常用结论
(当且仅当 时取等号).然后换元得到 ,分类讨论,利用不等式的基本性质
证得要证得不等式,有一定的巧合性.
4.(2021·北京·统考高考真题)已知函数 .
(1)若 ,求曲线 在点 处的切线方程;
(2)若 在 处取得极值,求 的单调区间,以及其最大值与最小值.
【答案】(1) ;(2)函数 的增区间为 、 ,单调递减区间为 ,最
大值为 ,最小值为 .
【分析】(1)求出 、 的值,利用点斜式可得出所求切线的方程;
(2)由 可求得实数 的值,然后利用导数分析函数 的单调性与极值,由此可得出结果.
【详解】(1)当 时, ,则 , , ,
25此时,曲线 在点 处的切线方程为 ,即 ;
(2)因为 ,则 ,
由题意可得 ,解得 ,
故 , ,列表如下:
极大
增 减 极小值 增
值
所以,函数 的增区间为 、 ,单调递减区间为 .
当 时, ;当 时, .
所以, , .
5.(2021·天津·统考高考真题)已知 ,函数 .
(I)求曲线 在点 处的切线方程:
(II)证明 存在唯一的极值点
(III)若存在a,使得 对任意 成立,求实数b的取值范围.
【答案】(I) ;(II)证明见解析;(III)
【分析】(I)求出 在 处的导数,即切线斜率,求出 ,即可求出切线方程;
(II)令 ,可得 ,则可化为证明 与 仅有一个交点,利用导数求出 的
变化情况,数形结合即可求解;
(III)令 ,题目等价于存在 ,使得 ,即 ,利用导
数即可求出 的最小值.
【详解】(I) ,则 ,
又 ,则切线方程为 ;
(II)令 ,则 ,
26令 ,则 ,
当 时, , 单调递减;当 时, , 单调递增,
当 时, , ,当 时, ,画出 大致图像如下:
所以当 时, 与 仅有一个交点,令 ,则 ,且 ,
当 时, ,则 , 单调递增,
当 时, ,则 , 单调递减,
为 的极大值点,故 存在唯一的极值点;
(III)由(II)知 ,此时 ,
所以 ,
令 ,
若存在a,使得 对任意 成立,等价于存在 ,使得 ,即 ,
, ,
当 时, , 单调递减,当 时, , 单调递增,
所以 ,故 ,
所以实数b的取值范围 .
【点睛】关键点睛:第二问解题的关键是转化为证明 与 仅有一个交点;第三问解题的关键是
转化为存在 ,使得 ,即 .
6.(2020·山东·统考高考真题)已知函数 .
(1)当 时,求曲线 在点 处的切线与两坐标轴围成的三角形的面积;
(2)若不等式 恒成立,求a的取值范围.
【答案】(1) (2)
27【分析】(1)利用导数的几何意义求出在点 切线方程,即可得到坐标轴交点坐标,最后根据三角
形面积公式得结果;
(2)方法一:利用导数研究函数 的单调性,当a=1时,由 得 ,符合题意;
当a>1时,可证 ,从而 存在零点 ,使得 ,得到 ,利
用零点的条件,结合指数对数的运算化简后,利用基本不等式可以证得 恒成立;当 时,研
究 .即可得到不符合题意.综合可得a的取值范围.
【详解】(1) , , .
,∴切点坐标为(1,1+e),
∴函数 在点(1,f(1)处的切线方程为 ,即 ,
切线与坐标轴交点坐标分别为 ,
∴所求三角形面积为 .
(2)[方法一]:通性通法
, ,且 .
设 ,则
∴g(x)在 上单调递增,即 在 上单调递增,
当 时, ,∴ ,∴ 成立.
当 时, , , ,
∴存在唯一 ,使得 ,且当 时 ,当 时 ,
, ,
因此
>1,
∴ ∴ 恒成立;
当 时, ∴ 不是恒成立.
28综上所述,实数a的取值范围是[1,+∞).
[方法二]【最优解】:同构
由 得 ,即 ,而 ,所以
.
令 ,则 ,所以 在R上单调递增.
由 ,可知 ,所以 ,所以
.
令 ,则 .
所以当 时, 单调递增;
当 时, 单调递减.
所以 ,则 ,即 .
所以a的取值范围为 .
[方法三]:换元同构
由题意知 ,令 ,所以 ,所以 .
于是 .
由于 ,而 在 时为增函数,故 ,即
,分离参数后有 .
令 ,所以 .
当 时, 单调递增;当 时, 单调递减.
所以当 时, 取得最大值为 .所以 .
[方法四]:
因为定义域为 ,且 ,所以 ,即 .
令 ,则 ,所以 在区间 内单调递增.
因为 ,所以 时,有 ,即 .
下面证明当 时, 恒成立.
令 ,只需证当 时, 恒成立.
因为 ,所以 在区间 内单调递增,则 .
因此要证明 时, 恒成立,只需证明 即可.
29由 ,得 .
上面两个不等式两边相加可得 ,故 时, 恒成立.
当 时,因为 ,显然不满足 恒成立.
所以a的取值范围为 .
【整体点评】(2)方法一:利用导数判断函数 的单调性,求出其最小值,由 即可求出,解法
虽稍麻烦,但是此类题,也是本题的通性通法;
方法二:利用同构思想将原不等式化成 ,再根据函数 的单调性
以及分离参数法即可求出,是本题的最优解;
方法三:通过先换元,令 ,再同构,可将原不等式化成 ,再根据函数 的
单调性以及分离参数法求出;
方法四:由特殊到一般,利用 可得 的取值范围,再进行充分性证明即可.
7.(2020年全国新高考Ⅰ卷)设函数 ,曲线 在点( ,f( ))处的切线与y轴垂直.
(1)求b.
(2)若 有一个绝对值不大于1的零点,证明: 所有零点的绝对值都不大于1.
【答案】(1) ;(2)证明见解析
【分析】(1)利用导数的几何意义得到 ,解方程即可;
(2)方法一:由(1)可得 ,易知 在 上单调递减,在 ,
上单调递增,且 ,采用反证法,推出矛盾即可.
【详解】(1)因为 ,由题意, ,即: ,则 .
(2)[方法一]:通性通法
由(1)可得 , ,
令 ,得 或 ;令 ,得 ,
所以 在 上单调递减,在 , 上单调递增,
且 ,
若 所有零点中存在一个绝对值大于1的零点 ,则 或 ,
30即 或 .
当 时, ,
又 ,
由零点存在性定理知 在 上存在唯一一个零点 ,
即 在 上存在唯一一个零点,在 上不存在零点,
此时 不存在绝对值不大于1的零点,与题设矛盾;
当 时, ,
又 ,
由零点存在性定理知 在 上存在唯一一个零点 ,
即 在 上存在唯一一个零点,在 上不存在零点,
此时 不存在绝对值不大于1的零点,与题设矛盾;
综上, 所有零点的绝对值都不大于1.
[方法二]【最优解】:
设 是 的一个零点,且 ,则 .
从而 .
令 ,由判别式 ,可知 在R上有解, 的对
称轴是 ,所以 在区间 上有一根为 ,
在区间 上有一根为 (当 时, ),进而有 ,所以 的所有零点的绝
对值均不大于1.
[方法三]:
设 是函数 的一个绝对值不大于1的零点,且 .设 ,则
,显然 在区间 内单调递减,在区间 内单调递增,在区间 内单调
递减.又 ,于是 的值域为 .
31设 为函数 的零点,则必有 ,于是 ,所以
解得 ,即 .
综上, 的所有零点的绝对值都不大于1.
[方法四]:
由(1)知, ,令 ,得 或 .则 在区间
内递增,在区间 内递减,在区间 内递增,所以 的极大值为
的极小值为 .
(ⅰ)若 ,即 或 , 有唯一一个零点 ,显然有 ,不满足题意;
(ⅱ)若 ,即 或 , 有两个零点,不妨设一个零点为 ,显然有
,此时, ,则 ,另一个零点为1,满足题意;同理,若一个零点为 ,
则另一个零点为 .
(ⅲ)若 ,即 , 有三个零点,易知在区间 内有一个零点,不妨设
为 ,显然有 ,又 , ,所以在 内有一个零点m,显然 ,同理,
在 内有一个零点n,有 .
综上, 所有零点的绝对值都不大于1.
[方法五]:
设 是 的一个零点且 ,则 是 的另一个零点.
.
则 ,设 ,由判别式 ,所以方程有
解.
假设实数 满足 .
32由 ,得 .与
矛盾,假设不成立.
所以, 所有零点的绝对值都不大于1.
【整体点评】(2)方法一:先通过研究函数的单调性,得出零点可能所在区间,再根据反证法思想即可
推出矛盾,是通性通法;方法二:利用零点的定义以及零点存在性定理即可求出,是本题的最优解;方法
三:利用零点的定义结合题意求出 的范围,然后再由零点定义以及 的范围即可求出所有零点的范围,
从而证出;方法四:由函数的单调性讨论极大值极小值的符号,得出 的范围,再结合零点存在性定理即
可证出;方法五:设函数的一个零点为 ,满足 ,再设另一个零点为 ,通过零点定义找到 的
关系,再根据一元二次方程存在解的条件以及反证法即可推出矛盾,从而证出.
8.(2019·北京·高考真题)已知函数 .
(Ⅰ)求曲线 的斜率为1的切线方程;
(Ⅱ)当 时,求证: ;
(Ⅲ)设 ,记 在区间 上的最大值为M(a),当M(a)最小时,
求a的值.
【答案】(Ⅰ) 和 .
(Ⅱ)见解析;
(Ⅲ) .
【分析】(Ⅰ)首先求解导函数,然后利用导函数求得切点的横坐标,据此求得切点坐标即可确定切线方程;
(Ⅱ)由题意分别证得 和 即可证得题中的结论;
(Ⅲ)由题意结合(Ⅱ)中的结论分类讨论即可求得a的值.
【详解】(Ⅰ) ,令 得 或者 .
当 时, ,此时切线方程为 ,即 ;
当 时, ,此时切线方程为 ,即 ;
综上可得所求切线方程为 和 .
(Ⅱ)设 , ,令 得 或者 ,所以当
时, , 为增函数;当 时, , 为减函数;当 时,
, 为增函数;
而 ,所以 ,即 ;
33同理令 ,可求其最小值为 ,所以 ,即 ,综上可
得 .
(Ⅲ)由(Ⅱ)知 ,
所以 是 中的较大者,
若 ,即 时, ;
若 ,即 时, ;
所以当 最小时, ,此时 .
【点睛】本题主要考查利用导函数研究函数的切线方程,利用导函数证明不等式的方法,分类讨论的数学
思想等知识,意在考查学生的转化能力和计算求解能力.
9.(2019·浙江·高考真题)已知实数 ,设函数
(1)当 时,求函数 的单调区间;
(2)对任意 均有 求 的取值范围.
注: 为自然对数的底数.
【答案】(1) 的单调递增区间是 ,单调递减区间是 ;(2) .
【分析】(1)首先求得导函数的解析式,然后结合函数的解析式确定函数的单调区间即可.
(2)由题意首先由函数在特殊点的函数值得到a的取值范围,然后证明所得的范围满足题意即可.
【详解】(1)当 时, ,函数的定义域为 ,且:
,
因此函数 的单调递增区间是 ,单调递减区间是 .
(2)由 ,得 ,
当 时, ,等价于 ,
令 ,则 ,
设 , ,
则 ,
34(i)当 时, ,
则 ,
记 ,
则
列表讨论:
x ( ) 1 (1,+∞)
p′(x) ﹣ 0 +
P(x) p( ) 单调递减 极小值p(1) 单调递增
(ii)当 时, ,
令 ,
则 ,
故 在 上单调递增, ,
由(i)得 ,
,
由(i)(ii)知对任意 ,
即对任意 ,均有 ,
综上所述,所求的a的取值范围是 .
【点睛】导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,对导
数的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系.
35(2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)利用导数求函数的最值(极值),解
决生活中的优化问题. (4)考查数形结合思想的应用.
考点 03 三角函数相关导数问题
一、解答题
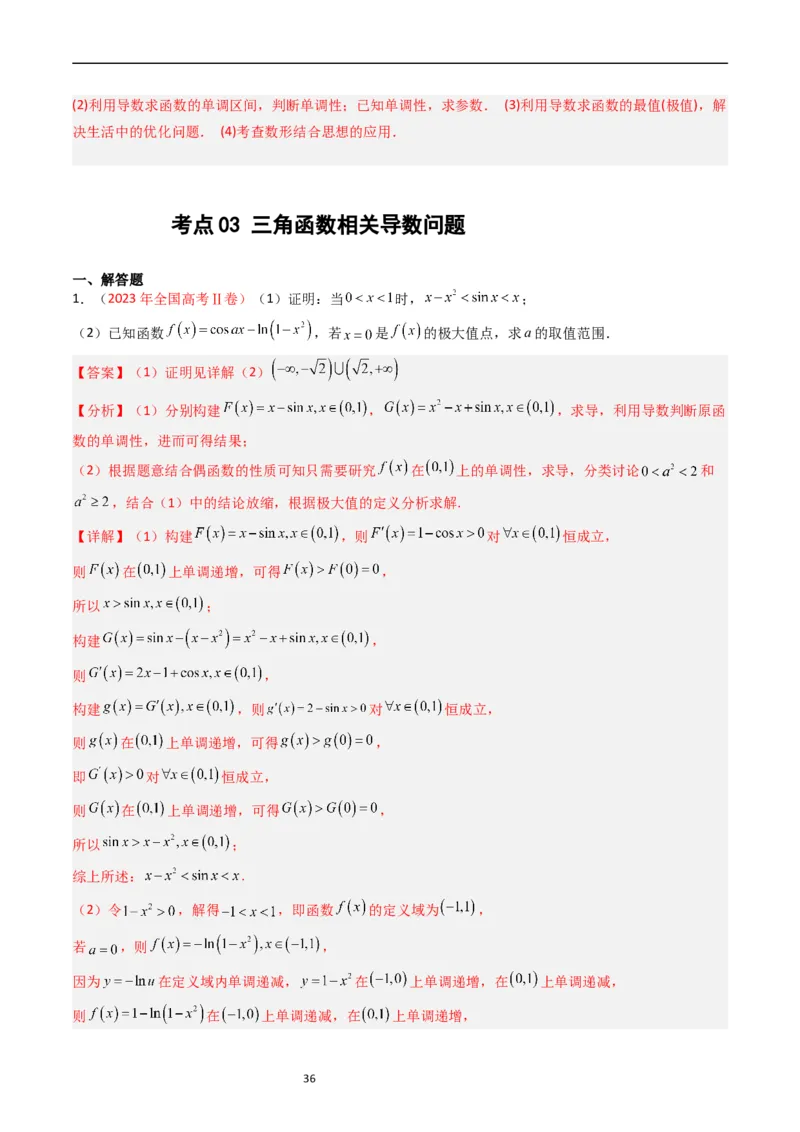
1.(2023年全国高考Ⅱ卷)(1)证明:当 时, ;
(2)已知函数 ,若 是 的极大值点,求a的取值范围.
【答案】(1)证明见详解(2)
【分析】(1)分别构建 , ,求导,利用导数判断原函
数的单调性,进而可得结果;
(2)根据题意结合偶函数的性质可知只需要研究 在 上的单调性,求导,分类讨论 和
,结合(1)中的结论放缩,根据极大值的定义分析求解.
【详解】(1)构建 ,则 对 恒成立,
则 在 上单调递增,可得 ,
所以 ;
构建 ,
则 ,
构建 ,则 对 恒成立,
则 在 上单调递增,可得 ,
即 对 恒成立,
则 在 上单调递增,可得 ,
所以 ;
综上所述: .
(2)令 ,解得 ,即函数 的定义域为 ,
若 ,则 ,
因为 在定义域内单调递减, 在 上单调递增,在 上单调递减,
则 在 上单调递减,在 上单调递增,
36故 是 的极小值点,不合题意,所以 .
当 时,令
因为 ,
且 ,
所以函数 在定义域内为偶函数,
由题意可得: ,
(i)当 时,取 , ,则 ,
由(1)可得 ,
且 ,
所以 ,
即当 时, ,则 在 上单调递增,
结合偶函数的对称性可知: 在 上单调递减,
所以 是 的极小值点,不合题意;
(ⅱ)当 时,取 ,则 ,
由(1)可得 ,
构建 ,
则 ,
且 ,则 对 恒成立,
可知 在 上单调递增,且 ,
所以 在 内存在唯一的零点 ,
当 时,则 ,且 ,
则 ,
37即当 时, ,则 在 上单调递减,
结合偶函数的对称性可知: 在 上单调递增,
所以 是 的极大值点,符合题意;
综上所述: ,即 ,解得 或 ,
故a的取值范围为 .
【点睛】关键点睛:
1.当 时,利用 ,换元放缩;
2.当 时,利用 ,换元放缩.
2.(2023·全国甲卷)已知函数
(1)当 时,讨论 的单调性;
(2)若 恒成立,求a的取值范围.
【答案】(1)答案见解析.(2)
【分析】(1)求导,然后令 ,讨论导数的符号即可;
(2)构造 ,计算 的最大值,然后与0比较大小,得出 的分界点,再对 讨论即可.
【详解】(1)
令 ,则
则
当
当 ,即 .
当 ,即 .
所以 在 上单调递增,在 上单调递减
(2)设
38设
所以 .
若 ,
即 在 上单调递减,所以 .
所以当 ,符合题意.
若
当 ,所以 .
.
所以 ,使得 ,即 ,使得 .
当 ,即当 单调递增.
所以当 ,不合题意.
综上, 的取值范围为 .
【点睛】关键点点睛:本题采取了换元,注意复合函数的单调性 在定义域内是减函数,若 ,当
,对应当 .
3.(2022·天津·统考高考真题)已知 ,函数
(1)求函数 在 处的切线方程;
(2)若 和 有公共点,
(i)当 时,求 的取值范围;
(ii)求证: .
【答案】(1)
(2)(i) ;(ii)证明见解析
【分析】(1)求出 可求切线方程;
39(2)(i)当 时,曲线 和 有公共点即为 在 上有零点,求导
后分类讨论结合零点存在定理可求 .
(ii)曲线 和 有公共点即 ,利用点到直线的距离得到
,利用导数可证 ,从而可得不等式成立.
【详解】(1) ,故 ,而 ,
曲线 在点 处的切线方程为 即 .
(2)(i)当 时,
因为曲线 和 有公共点,故 有解,
设 ,故 ,故 在 上有解,
设 ,故 在 上有零点,
而 ,
若 ,则 恒成立,此时 在 上无零点,
若 ,则 在 上恒成立,故 在 上为增函数,
而 , ,故 在 上无零点,
故 ,
设 ,则 ,
故 在 上为增函数,
而 , ,
故 在 上存在唯一零点 ,
且 时, ; 时, ;
故 时, ; 时, ;
所以 在 上为减函数,在 上为增函数,
故 ,
因为 在 上有零点,故 ,故 ,
而 ,故 即 ,
设 ,则 ,
40故 在 上为增函数,
而 ,故 .
(ii)因为曲线 和 有公共点,
所以 有解 ,其中 ,
若 ,则 ,该式不成立,故 .
故 ,考虑直线 ,
表示原点与直线 上的动点 之间的距离,
故 ,所以 ,
下证:对任意 ,总有 ,
证明:当 时,有 ,故 成立.
当 时,即证 ,
设 ,则 (不恒为零),
故 在 上为减函数,故 即 成立.
综上, 成立.
下证:当 时, 恒成立,
,则 ,
故 在 上为增函数,故 即 恒成立.
下证: 在 上恒成立,即证: ,
即证: ,即证: ,
而 ,故 成立.
故 ,即 成立.
【点睛】思路点睛:导数背景下零点问题,注意利用函数的单调性结合零点存在定理来处理,而多变量的
不等式的成立问题,注意从几何意义取构建不等式关系,再利用分析法来证明目标不等式.
4.(2020年全国高考Ⅱ卷)已知函数f(x)=sin2xsin2x.
(1)讨论f(x)在区间(0,π)的单调性;
41(2)证明: ;
(3)设n∈N*,证明:sin2xsin22xsin24x…sin22nx≤ .
【答案】(1)当 时, 单调递增,当 时, 单调递减,
当 时, 单调递增.
(2)证明见解析;
(3)证明见解析.
【分析】(1)首先求得导函数的解析式,然后由导函数的零点确定其在各个区间上的符号,最后确定原函数
的单调性即可;
(2)[方法一]由题意将所给的式子进行变形,利用四元基本不等式即可证得题中的不等式;
(3)[方法一]将所给的式子进行恒等变形,构造出(2)的形式,利用(2)的结论即可证得题中的不等式.
【详解】(1)由函数的解析式可得: ,则:
,
在 上的根为: ,
当 时, 单调递增,
当 时, 单调递减,
当 时, 单调递增.
(2)[方法一]【最优解】:基本不等式法
由四元均值不等式可得
,当且仅当 ,
即 或 时等号成立.
所以 .
[方法二]:构造新函数+齐次化方法
42因为 ,令 ,则问题转化为求
的最大值.
求导得 ,令 ,得 .
当 时, ,函数 单调递增;
当 时, ,函数 单调递减.
所以函数 的最大值为 ,故 .
[方法三]:结合函数的周期性进行证明
注意到 ,
故函数 是周期为 的函数,
结合(1)的结论,计算可得: ,
, ,
据此可得: , ,
即 .
(3)利用(2)的结论
由于
,
所以 .
【整体点评】(2)方法一:基本不等式是证明不等式的重要工具,利用基本不等式解题时一定要注意等号成
立的条件;
方法二:齐次化之后切化弦是一种常用的方法,它将原问题转化为一元函数的问题,然后构造函数即可证
得题中的不等式;
方法三:周期性是三角函数的重要特征,结合函数的周期性和函数的最值证明不等式充分体现了三角函数
有界限的应用.
(3)方法一:利用(2)的结论体现了解答题的出题思路,逐问递进是解答题常见的设问方式;
435.(2019·天津·高考真题)设函数 为 的导函数.
(Ⅰ)求 的单调区间;
(Ⅱ)当 时,证明 ;
(Ⅲ)设 为函数 在区间 内的零点,其中 ,证明
.
【答案】(Ⅰ)单调递增区间为 的单调递减区间为
.(Ⅱ)见证明;(Ⅲ)见证明
【分析】(Ⅰ)由题意求得导函数的解析式,然后由导函数的符号即可确定函数 的单调区间;
(Ⅱ)构造函数 ,结合(Ⅰ)的结果和导函数的符号求解函数 的最小值即可证得
题中的结论;
(Ⅲ)令 ,结合(Ⅰ),(Ⅱ)的结论、函数的单调性和零点的性质放缩不等式即可证得题中的结果.
【详解】(Ⅰ)由已知,有 .
当 时,有 ,得 ,则 单调递减;
当 时,有 ,得 ,则 单调递增.
所以, 的单调递增区间为 ,
的单调递减区间为 .
(Ⅱ)记 .依题意及(Ⅰ)有: ,
从而 .当 时, ,故
.
因此, 在区间 上单调递减,进而 .
44所以,当 时, .
(Ⅲ)依题意, ,即 .
记 ,则 .
且 .
由 及(Ⅰ)得 .
由(Ⅱ)知,当 时, ,所以 在 上为减函数,
因此 .
又由(Ⅱ)知 ,故:
.
所以 .
考点 04 导数类综合问题
一、解答题
1.(2023·全国乙卷)已知函数 .
(1)当 时,求曲线 在点 处的切线方程;
(2)是否存在a,b,使得曲线 关于直线 对称,若存在,求a,b的值,若不存在,说明理由.
(3)若 在 存在极值,求a的取值范围.
【答案】(1) ;
(2)存在 满足题意,理由见解析.
45(3) .
【分析】(1)由题意首先求得导函数的解析式,然后由导数的几何意义确定切线的斜率和切点坐标,最后求
解切线方程即可;
(2)首先求得函数的定义域,由函数的定义域可确定实数 的值,进一步结合函数的对称性利用特殊值法可
得关于实数 的方程,解方程可得实数 的值,最后检验所得的 是否正确即可;
(3)原问题等价于导函数有变号的零点,据此构造新函数 ,然后对函数求导,
利用切线放缩研究导函数的性质,分类讨论 , 和 三中情况即可求得实数 的取值范围.
【详解】(1)当 时, ,
则 ,
据此可得 ,
函数在 处的切线方程为 ,
即 .
(2)由函数的解析式可得 ,
函数的定义域满足 ,即函数的定义域为 ,
定义域关于直线 对称,由题意可得 ,
由对称性可知 ,
取 可得 ,
即 ,则 ,解得 ,
经检验 满足题意,故 .
即存在 满足题意.
(3)由函数的解析式可得 ,
由 在区间 存在极值点,则 在区间 上存在变号零点;
46令 ,
则 ,
令 ,
在区间 存在极值点,等价于 在区间 上存在变号零点,
当 时, , 在区间 上单调递减,
此时 , 在区间 上无零点,不合题意;
当 , 时,由于 ,所以 在区间 上单调递增,
所以 , 在区间 上单调递增, ,
所以 在区间 上无零点,不符合题意;
当 时,由 可得 ,
当 时, , 单调递减,
当 时, , 单调递增,
故 的最小值为 ,
令 ,则 ,
函数 在定义域内单调递增, ,
据此可得 恒成立,
则 ,
令 ,则 ,
当 时, 单调递增,
当 时, 单调递减,
故 ,即 (取等条件为 ),
所以 ,
47,且注意到 ,
根据零点存在性定理可知: 在区间 上存在唯一零点 .
当 时, , 单调减,
当 时, , 单调递增,
所以 .
令 ,则 ,
则函数 在 上单调递增,在 上单调递减,
所以 ,所以 ,
所以
,
所以函数 在区间 上存在变号零点,符合题意.
综合上面可知:实数 得取值范围是 .
【点睛】(1)求切线方程的核心是利用导函数求切线的斜率,求函数的导数要准确地把函数拆分成基本初等
函数的和、差、积、商,再利用运算法则求导,合函数求导,应由外到内逐层求导,必要时要进行换元.
(2)根据函数的极值(点)求参数的两个要领:①列式:根据极值点处导数为0和极值这两个条件列方程组,利
用待定系数法求解;②验证:求解后验证根的合理性.本题中第二问利用对称性求参数值之后也需要进行验证.
2.(2022·全国甲卷)已知函数 .
(1)若 ,求a的取值范围;
(2)证明:若 有两个零点 ,则 .
【答案】(1)
48(2)证明见的解析
【分析】(1)由导数确定函数单调性及最值,即可得解;
(2)利用分析法,转化要证明条件为 ,再利用导数即可得证.
【详解】(1)[方法一]:常规求导
的定义域为 ,则
令 ,得
当 单调递减
当 单调递增 ,
若 ,则 ,即
所以 的取值范围为
[方法二]:同构处理
由 得:
令 ,则 即
令 ,则
故 在区间 上是增函数
故 ,即
所以 的取值范围为
(2)[方法一]:构造函数
由题知, 一个零点小于1,一个零点大于1,不妨设
要证 ,即证
因为 ,即证
又因为 ,故只需证
即证
即证
49下面证明 时,
设 ,
则
设
所以 ,而
所以 ,所以
所以 在 单调递增
即 ,所以
令
所以 在 单调递减
即 ,所以 ;
综上, ,所以 .
[方法二]:对数平均不等式
由题意得:
令 ,则 ,
所以 在 上单调递增,故 只有1个解
又因为 有两个零点 ,故
两边取对数得: ,即
50又因为 ,故 ,即
下证
因为
不妨设 ,则只需证
构造 ,则
故 在 上单调递减
故 ,即 得证
【点睛】关键点点睛 :本题是极值点偏移问题,关键点是通过分析法,构造函数证明不等式
这个函数经常出现,需要掌握
3.(2022年全国新高考Ⅰ卷)已知函数 和 有相同的最小值.
(1)求a;
(2)证明:存在直线 ,其与两条曲线 和 共有三个不同的交点,并且从左到右的三个交
点的横坐标成等差数列.
【答案】(1)
(2)见解析
【分析】(1)根据导数可得函数的单调性,从而可得相应的最小值,根据最小值相等可求a.注意分类讨
论.
(2)根据(1)可得当 时, 的解的个数、 的解的个数均为2,构建新函数
,利用导数可得该函数只有一个零点且可得 的大小关系,根据存在直线
与曲线 、 有三个不同的交点可得 的取值,再根据两类方程的根的关系可证明三根
成等差数列.
【详解】(1) 的定义域为 ,而 ,
若 ,则 ,此时 无最小值,故 .
的定义域为 ,而 .
51当 时, ,故 在 上为减函数,
当 时, ,故 在 上为增函数,
故 .
当 时, ,故 在 上为减函数,
当 时, ,故 在 上为增函数,
故 .
因为 和 有相同的最小值,
故 ,整理得到 ,其中 ,
设 ,则 ,
故 为 上的减函数,而 ,
故 的唯一解为 ,故 的解为 .
综上, .
(2)[方法一]:
由(1)可得 和 的最小值为 .
当 时,考虑 的解的个数、 的解的个数.
设 , ,
当 时, ,当 时, ,
故 在 上为减函数,在 上为增函数,
所以 ,
而 , ,
设 ,其中 ,则 ,
故 在 上为增函数,故 ,
故 ,故 有两个不同的零点,即 的解的个数为2.
设 , ,
52当 时, ,当 时, ,
故 在 上为减函数,在 上为增函数,
所以 ,
而 , ,
有两个不同的零点即 的解的个数为2.
当 ,由(1)讨论可得 、 仅有一个解,
当 时,由(1)讨论可得 、 均无根,
故若存在直线 与曲线 、 有三个不同的交点,
则 .
设 ,其中 ,故 ,
设 , ,则 ,
故 在 上为增函数,故 即 ,
所以 ,所以 在 上为增函数,
而 , ,
故 上有且只有一个零点 , 且:
当 时, 即 即 ,
当 时, 即 即 ,
因此若存在直线 与曲线 、 有三个不同的交点,
故 ,
此时 有两个不同的根 ,
此时 有两个不同的根 ,
故 , , ,
所以 即 即 ,
故 为方程 的解,同理 也为方程 的解
又 可化为 即 即 ,
故 为方程 的解,同理 也为方程 的解,
53所以 ,而 ,
故 即 .
[方法二]:
由 知, , ,
且 在 上单调递减,在 上单调递增;
在 上单调递减,在 上单调递增,且
① 时,此时 ,显然 与两条曲线 和
共有0个交点,不符合题意;
② 时,此时 ,
故 与两条曲线 和 共有2个交点,交点的横坐标分别为0和1;
③ 时,首先,证明 与曲线 有2个交点,
即证明 有2个零点, ,
所以 在 上单调递减,在 上单调递增,
又因为 , , ,
令 ,则 ,
所以 在 上存在且只存在1个零点,设为 ,在 上存在且只存在1个零点,设
为
其次,证明 与曲线和 有2个交点,
即证明 有2个零点, ,
所以 上单调递减,在 上单调递增,
又因为 , , ,
令 ,则 ,
所以 在 上存在且只存在1个零点,设为 ,在 上存在且只存在1个零点,设为
再次,证明存在b,使得
因为 ,所以 ,
若 ,则 ,即 ,
所以只需证明 在 上有解即可,
即 在 上有零点,
54因为 , ,
所以 在 上存在零点,取一零点为 ,令 即可,
此时取
则此时存在直线 ,其与两条曲线 和 共有三个不同的交点,
最后证明 ,即从左到右的三个交点的横坐标成等差数列,
因为
所以 ,
又因为 在 上单调递减, , 即 ,所以 ,
同理,因为 ,
又因为 在 上单调递增, 即 , ,所以 ,
又因为 ,所以 ,
即直线 与两条曲线 和 从左到右的三个交点的横坐标成等差数列.
【点睛】思路点睛:函数的最值问题,往往需要利用导数讨论函数的单调性,此时注意对参数的分类讨论,
而不同方程的根的性质,注意利用方程的特征找到两类根之间的关系.
4.(20122年全国高考Ⅱ卷)已知函数 .
(1)当 时,讨论 的单调性;
(2)当 时, ,求a的取值范围;
(3)设 ,证明: .
【答案】(1) 的减区间为 ,增区间为 .
(2)
(3)见解析
55【分析】(1)求出 ,讨论其符号后可得 的单调性.
(2)设 ,求出 ,先讨论 时题设中的不等式不成立,再就 结合放缩
法讨论 符号,最后就 结合放缩法讨论 的范围后可得参数的取值范围.
(3)由(2)可得 对任意的 恒成立,从而可得 对任意的 恒成立,
结合裂项相消法可证题设中的不等式.
【详解】(1)当 时, ,则 ,
当 时, ,当 时, ,
故 的减区间为 ,增区间为 .
(2)设 ,则 ,
又 ,设 ,
则 ,
若 ,则 ,
因为 为连续不间断函数,
故存在 ,使得 ,总有 ,
故 在 为增函数,故 ,
故 在 为增函数,故 ,与题设矛盾.
若 ,则 ,
下证:对任意 ,总有 成立,
证明:设 ,故 ,
故 在 上为减函数,故 即 成立.
由上述不等式有 ,
故 总成立,即 在 上为减函数,
所以 .
当 时,有 ,
所以 在 上为减函数,所以 .
56综上, .
(3)取 ,则 ,总有 成立,
令 ,则 ,
故 即 对任意的 恒成立.
所以对任意的 ,有 ,
整理得到: ,
故
,
故不等式成立.
【点睛】思路点睛:函数参数的不等式的恒成立问题,应该利用导数讨论函数的单调性,注意结合端点处
导数的符号合理分类讨论,导数背景下数列不等式的证明,应根据已有的函数不等式合理构建数列不等式.
5.(2022·天津·统考高考真题)已知 ,函数
(1)求函数 在 处的切线方程;
(2)若 和 有公共点,
(i)当 时,求 的取值范围;
(ii)求证: .
【答案】(1)
(2)(i) ;(ii)证明见解析
【分析】(1)求出 可求切线方程;
(2)(i)当 时,曲线 和 有公共点即为 在 上有零点,求导
后分类讨论结合零点存在定理可求 .
(ii)曲线 和 有公共点即 ,利用点到直线的距离得到
,利用导数可证 ,从而可得不等式成立.
57【详解】(1) ,故 ,而 ,
曲线 在点 处的切线方程为 即 .
(2)(i)当 时,
因为曲线 和 有公共点,故 有解,
设 ,故 ,故 在 上有解,
设 ,故 在 上有零点,
而 ,
若 ,则 恒成立,此时 在 上无零点,
若 ,则 在 上恒成立,故 在 上为增函数,
而 , ,故 在 上无零点,
故 ,
设 ,则 ,
故 在 上为增函数,
而 , ,
故 在 上存在唯一零点 ,
且 时, ; 时, ;
故 时, ; 时, ;
所以 在 上为减函数,在 上为增函数,
故 ,
因为 在 上有零点,故 ,故 ,
而 ,故 即 ,
设 ,则 ,
故 在 上为增函数,
而 ,故 .
(ii)因为曲线 和 有公共点,
所以 有解 ,其中 ,
若 ,则 ,该式不成立,故 .
58故 ,考虑直线 ,
表示原点与直线 上的动点 之间的距离,
故 ,所以 ,
下证:对任意 ,总有 ,
证明:当 时,有 ,故 成立.
当 时,即证 ,
设 ,则 (不恒为零),
故 在 上为减函数,故 即 成立.
综上, 成立.
下证:当 时, 恒成立,
,则 ,
故 在 上为增函数,故 即 恒成立.
下证: 在 上恒成立,即证: ,
即证: ,即证: ,
而 ,故 成立.
故 ,即 成立.
【点睛】思路点睛:导数背景下零点问题,注意利用函数的单调性结合零点存在定理来处理,而多变量的
不等式的成立问题,注意从几何意义取构建不等式关系,再利用分析法来证明目标不等式.
6.(2021·全国乙卷)设函数 ,已知 是函数 的极值点.
(1)求a;
(2)设函数 .证明: .
【答案】(1) ;(2)证明见详解
【分析】(1)由题意求出 ,由极值点处导数为0即可求解出参数 ;
(2)由(1)得 , 且 ,分类讨论 和 ,可等价转化为要证
,即证 在 和 上恒成立,结合导数和换元法即可求解
59【详解】(1)由 , ,
又 是函数 的极值点,所以 ,解得 ;
(2)[方法一]:转化为有分母的函数
由(Ⅰ)知, ,其定义域为 .
要证 ,即证 ,即证 .
(ⅰ)当 时, , ,即证 .令 ,因为
,所以 在区间 内为增函数,所以 .
(ⅱ)当 时, , ,即证 ,由(ⅰ)分析知 在区间
内为减函数,所以 .
综合(ⅰ)(ⅱ)有 .
[方法二] 【最优解】:转化为无分母函数
由(1)得 , , 且 ,
当 时,要证 , , ,即证
,化简得 ;
同理,当 时,要证 , , ,即证
,化简得 ;
令 ,再令 ,则 , ,
令 , ,
当 时, , 单减,故 ;
当 时, , 单增,故 ;
综上所述, 在 恒成立.
[方法三] :利用导数不等式中的常见结论证明
令 ,因为 ,所以 在区间 内是增函数,在区间 内是减
60函数,所以 ,即 (当且仅当 时取等号).故当 且 时, 且
, ,即 ,所以 .
(ⅰ)当 时, ,所以 ,即 ,所以 .
(ⅱ)当 时, ,同理可证得 .
综合(ⅰ)(ⅱ)得,当 且 时, ,即 .
【整体点评】(2)方法一利用不等式的性质分类转化分式不等式:当 时,转化为证明
,当 时,转化为证明 ,然后构造函数,利用导数研究单调性,进
而证得;方法二利用不等式的性质分类讨论分别转化为整式不等式:当 时, 成
立和当 时, 成立,然后换元构造,利用导数研究单调性进而证得,通性通法,
运算简洁,为最优解;方法三先构造函数 ,利用导数分析单调性,证得常见常用结论
(当且仅当 时取等号).然后换元得到 ,分类讨论,利用不等式的基本性质
证得要证得不等式,有一定的巧合性.
7.(2022年全国新高考Ⅰ卷)已知函数 .
(1)讨论 的单调性;
(2)设 , 为两个不相等的正数,且 ,证明: .
【答案】(1) 的递增区间为 ,递减区间为 ;(2)证明见解析.
【分析】(1) 首先确定函数的定义域,然后求得导函数的解析式,由导函数的符号即可确定原函数的单调
性.
(2)方法二:将题中的等式进行恒等变换,令 ,命题转换为证明: ,然后构造对称
差函数,结合函数零点的特征和函数的单调性即可证得题中的结论.
【详解】(1) 的定义域为 .
由 得, ,
当 时, ;当 时 ;当 时, .
故 在区间 内为增函数,在区间 内为减函数,
(2)[方法一]:等价转化
61由 得 ,即 .
由 ,得 .
由(1)不妨设 ,则 ,从而 ,得 ,
①令 ,
则 ,
当 时, , 在区间 内为减函数, ,
从而 ,所以 ,
由(1)得 即 .①
令 ,则 ,
当 时, , 在区间 内为增函数, ,
从而 ,所以 .
又由 ,可得 ,
所以 .②
由①②得 .
[方法二]【最优解】: 变形为 ,所以 .
令 .则上式变为 ,
于是命题转换为证明: .
令 ,则有 ,不妨设 .
由(1)知 ,先证 .
要证:
.
令 ,
则 ,
在区间 内单调递增,所以 ,即 .
62再证 .
因为 ,所以需证 .
令 ,
所以 ,故 在区间 内单调递增.
所以 .故 ,即 .
综合可知 .
[方法三]:比值代换
证明 同证法2.以下证明 .
不妨设 ,则 ,
由 得 , ,
要证 ,只需证 ,两边取对数得 ,
即 ,
即证 .
记 ,则 .
记 ,则 ,
所以, 在区间 内单调递减. ,则 ,
所以 在区间 内单调递减.
由 得 ,所以 ,
即 .
[方法四]:构造函数法
由已知得 ,令 ,
不妨设 ,所以 .
由(Ⅰ)知, ,只需证 .
证明 同证法2.
63再证明 .令 .
令 ,则 .
所以 , 在区间 内单调递增.
因为 ,所以 ,即
又因为 ,所以 ,
即 .
因为 ,所以 ,即 .
综上,有 结论得证.
【整体点评】(2)方法一:等价转化是处理导数问题的常见方法,其中利用的对称差函数,构造函数的思想,
这些都是导数问题必备的知识和技能.
方法二:等价转化是常见的数学思想,构造对称差函数是最基本的极值点偏移问题的处理策略.
方法三:比值代换是一种将双变量问题化为单变量问题的有效途径,然后构造函数利用函数的单调性证明
题中的不等式即可.
方法四:构造函数之后想办法出现关于 的式子,这是本方法证明不等式的关键思想所在.
8.(2022年全国新高考Ⅱ卷)已知函数 .
(1)讨论 的单调性;
(2)从下面两个条件中选一个,证明: 只有一个零点
① ;
② .
【答案】(1)答案见解析;(2)证明见解析.
【分析】(1)首先求得导函数的解析式,然后分类讨论确定函数的单调性即可;
(2)由题意结合(1)中函数的单调性和函数零点存在定理即可证得题中的结论.
【详解】(1)由函数的解析式可得: ,
当 时,若 ,则 单调递减,
若 ,则 单调递增;
64当 时,若 ,则 单调递增,
若 ,则 单调递减,
若 ,则 单调递增;
当 时, 在 上单调递增;
当 时,若 ,则 单调递增,
若 ,则 单调递减,
若 ,则 单调递增;
(2)若选择条件①:
由于 ,故 ,则 ,
而 ,
而函数在区间 上单调递增,故函数在区间 上有一个零点.
,
由于 , ,故 ,
结合函数的单调性可知函数在区间 上没有零点.
综上可得,题中的结论成立.
若选择条件②:
由于 ,故 ,则 ,
当 时, , ,
而函数在区间 上单调递增,故函数在区间 上有一个零点.
当 时,构造函数 ,则 ,
当 时, 单调递减,
65当 时, 单调递增,
注意到 ,故 恒成立,从而有: ,此时:
,
当 时, ,
取 ,则 ,
即: ,
而函数在区间 上单调递增,故函数在区间 上有一个零点.
,
由于 , ,故 ,
结合函数的单调性可知函数在区间 上没有零点.
综上可得,题中的结论成立.
9.(2020年全国高考Ⅲ卷)设函数 ,曲线 在点( ,f( ))处的切线与y轴垂直.
(1)求b.
(2)若 有一个绝对值不大于1的零点,证明: 所有零点的绝对值都不大于1.
【答案】(1) ;(2)证明见解析
【分析】(1)利用导数的几何意义得到 ,解方程即可;
(2)方法一:由(1)可得 ,易知 在 上单调递减,在 ,
上单调递增,且 ,采用反证法,推出矛盾即可.
【详解】(1)因为 ,由题意, ,即: ,则 .
66(2)[方法一]:通性通法
由(1)可得 , ,
令 ,得 或 ;令 ,得 ,
所以 在 上单调递减,在 , 上单调递增,
且 ,
若 所有零点中存在一个绝对值大于1的零点 ,则 或 ,
即 或 .
当 时, ,
又 ,
由零点存在性定理知 在 上存在唯一一个零点 ,
即 在 上存在唯一一个零点,在 上不存在零点,
此时 不存在绝对值不大于1的零点,与题设矛盾;
当 时, ,
又 ,
由零点存在性定理知 在 上存在唯一一个零点 ,
即 在 上存在唯一一个零点,在 上不存在零点,
此时 不存在绝对值不大于1的零点,与题设矛盾;
综上, 所有零点的绝对值都不大于1.
[方法二]【最优解】:
设 是 的一个零点,且 ,则 .
从而 .
令 ,由判别式 ,可知 在R上有解, 的对
称轴是 ,所以 在区间 上有一根为 ,
67在区间 上有一根为 (当 时, ),进而有 ,所以 的所有零点的绝
对值均不大于1.
[方法三]:
设 是函数 的一个绝对值不大于1的零点,且 .设 ,则
,显然 在区间 内单调递减,在区间 内单调递增,在区间 内单调
递减.又 ,于是 的值域为 .
设 为函数 的零点,则必有 ,于是 ,所以
解得 ,即 .
综上, 的所有零点的绝对值都不大于1.
[方法四]:
由(1)知, ,令 ,得 或 .则 在区间
内递增,在区间 内递减,在区间 内递增,所以 的极大值为
的极小值为 .
(ⅰ)若 ,即 或 , 有唯一一个零点 ,显然有 ,不满足题意;
(ⅱ)若 ,即 或 , 有两个零点,不妨设一个零点为 ,显然有
,此时, ,则 ,另一个零点为1,满足题意;同理,若一个零点为 ,
则另一个零点为 .
(ⅲ)若 ,即 , 有三个零点,易知在区间 内有一个零点,不妨设
为 ,显然有 ,又 , ,所以在 内有一个零点m,显然 ,同理,
在 内有一个零点n,有 .
综上, 所有零点的绝对值都不大于1.
68[方法五]:
设 是 的一个零点且 ,则 是 的另一个零点.
.
则 ,设 ,由判别式 ,所以方程有
解.
假设实数 满足 .
由 ,得 .与
矛盾,假设不成立.
所以, 所有零点的绝对值都不大于1.
69