2025一2026学年度上期高2027届期末考试数学答案_2024-2025高二（7-7月题库）_2026年1月高二_260128四川省成都市第七中学2025一2026学年度上期高二期末考试

2025—2026 学年度上期高 2024 级期末考试数学参考答案
一、选择题
1—4 BDCD 5—8 BBAA
二、多项选择题
9．BCD 10．BC 11．ACD
三、填空题.
3x 3
12．y =± 13． 14．52
2 4
四、解答题：本题共5小题，共77分，解答应写出文字说明，证明过程或演算步骤.
15．【详解】（1）设数列a 的首项为a ，公差为d，
n 1
S 2a d 22,
则 2 1 解得a 12,d 2，故a 的通项公式为a 122n12n14.…………6分
 a a 6d 0, 1 n n
7 1
2n1412n
（2）由（1）可知，S  nn13，
n 2
S
12n13n n25n
所以b  n n13.易知b 为等差数列.设b 的前n项和为T ，则T   ，
n n n n n n 2 2
 
202520 132513
所以数列 b 的前20项和为T 2T  2 106.…………………………13分
n 20 13 2 2
20
16．【详解】（1）因为圆C经过M 1,2  ,N  1,0  两点，所以线段MN 的斜率为k  1．因为圆
MN 11
C的圆心在直线2x y 0上，所以设圆C的圆心为  t,2t  ，
11 20 2t1
线段AB的中点为D ,   0,1  ，所以k  1，解得t 1，所以C  1,2  ，
 2 2  CD t
CA   11 2 22 2 2. 故圆C的方程为 x1 2  y2 2 4．………………………………7分
|k2k| 2
（2）依题意知k 0，圆心C  1,2  到直线l :kx yk 0的距离d   ，
2 k2 12 k2 1
因为直线l :kx yk 0与圆C相交于A,B两点，所以弦长
2
4 k
| AB|2 r2d2 2 4 4 ，
k2 1 k2 1
1 1 k 2 4k 4
S  |AB|d  4    2
所以 ABC 2 2 k2 1 k2 1 k2 1
k 
1 .当且仅当k 1时等号成立
k
故ABC 面积的最大值为2． …………………………………………………………15分
17．【详解】（1）由频率分布直方图易知，0.0400.0300.016a0.004101，解得a0.010，
由图知，90,100的频率为0.04．80,100的频率为0.10.040.14，
所以获奖学生最低分数线落在 80,90内，不妨设为x，则90x0.010.040.1，解得x84，
所以估计获奖学生的最低分数线为84分．……………………………………………………4分
（2）由图可知， 70,80与 80,90的频率之比是0.4:0.14:1，
由分层随机抽样的方法可知，在 70,80内抽取4人，记为a,a ,a ,a ，在 80,90内抽取1人，记为b，
1 2 3 4
从这5人中选取2人，则该试验的样本空间为：
1Ωa ,a ,a ,a ,a ,a ,a ,b,a ,a ,a ,a ,a ,b,a ,a ,a ,b,a ,b ,则nΩ10，
1 2 1 3 1 4 1 2 3 2 4 2 3 4 3 4
记事件A“这2人中恰有1人的成绩落在 70,80内”，则A a,b,a ,b,a ,b,a ,b ，则nA4，由古
1 2 3 4
nA
4 2
典概型概率公式，可得PA   ．…………………………………………9分
nΩ 10 5
（3）样本数据在 70,80内的人数为0.410040，在 80,90内的人数为0.110010，
x 40 77 10 8278，s2  40  9 7877 2 10  4  7882 212 ．
4010 4010 4010   4010  
所以这两组数据合并后的平均数x为78，总方差s2为12．………………………………15分
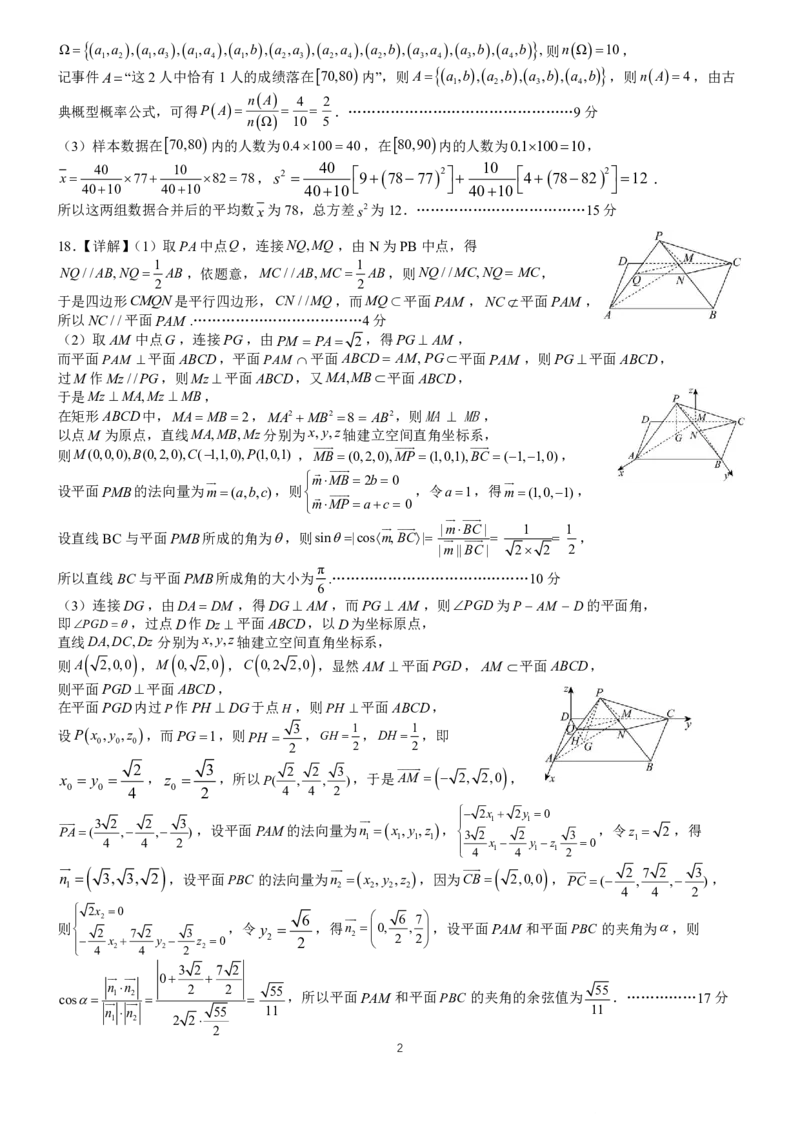
18．【详解】（1）取PA中点Q，连接NQ,MQ，由N为PB中点，得
1 1
NQ//AB,NQ AB，依题意，MC//AB,MC  AB，则NQ//MC,NQ MC，
2 2
于是四边形CMQN是平行四边形，CN //MQ，而MQÌ平面PAM ，NC平面PAM ，
所以NC//平面PAM .………………………………4分
（2）取AM 中点G，连接PG，由PM  PA 2，得PG^AM ，
而平面PAM 平面ABCD，平面PAM 平面ABCD AM,PG平面PAM ，则PG平面ABCD，
过M 作Mz//PG，则Mz平面ABCD，又MA,MB平面ABCD，
于是MzMA,MzMB，
在矩形ABCD中，MAMB2，MA2MB2 8 AB2，则MA MB，
以点M 为原点，直线MA,MB,Mz分别为x,y,z轴建立空间直角坐标系，
  
则M(0,0,0),B(0,2,0),C(1,1,0),P(1,0,1) ，MB(0,2,0),MP(1,0,1),BC (1,1,0)，
 
  mMB2b0 
设平面PMB的法向量为m(a,b,c)，则   ，令a1，得m(1,0,1)，
mMPac 0
 
  |mBC| 1 1
设直线BC与平面PMB所成的角为，则sin|cosm,BC|     ，
|m||BC| 2 2 2
π
所以直线BC与平面PMB所成角的大小为 .……………………………………10分
6
（3）连接DG，由DADM ，得DG AM，而PG^AM ，则PGD为P AM D的平面角，
即PGD，过点D作Dz 平面ABCD，以D为坐标原点，
直线DA,DC,Dz 分别为x,y,z轴建立空间直角坐标系，
     
则A 2,0,0 ，M 0, 2,0 ，C 0,2 2,0 ，显然AM 平面PGD，AM 平面ABCD，
则平面PGD平面ABCD，
在平面PGD内过P作PH DG于点H ，则PH 平面ABCD，
设Px ,y ,z ，而PG1，则PH  3 ，GH  1 ，DH  1 ，即
0 0 0 2 2 2
2 3 2 2 3   
x  y  ，z  ，所以P( , , )，于是AM   2, 2,0 ，
0 0 4 0 2 4 4 2
 2x  2y 0
 P  A  ( 3 4 2 , 4 2 , 2 3 )，设平面PAM的法向量为n  1 x 1 ,y 1 ,z 1 ，    3 2 x 1  2 1 y z 3 0 ，令z 1  2，得
 4 1 4 1 1 2
n    3, 3, 2  ，设平面PBC 的法向量为n  x ,y ,z ，因为C  B    2,0,0  ，  P  C  ( 2 , 7 2 , 3 )，
1 2 2 2 2
4 4 2
 2x 0
 2 6   6 7
则  2 x  7 2 y  3 z 0 ，令 y 2  2 ，得n 2    0, 2 , 2    ，设平面PAM 和平面PBC 的夹角为，则
 4 2 4 2 2 2
3 2 7 2
  0 
cos  n  1 n  2   2 2  55 ，所以平面PAM 和平面PBC 的夹角的余弦值为 55 ．……………17分
n n 55 11 11
1 2 2 2
2
22a2
 y2
19．【详解】（1）由题意可得 4 12 ，解得a2 1,b2 4，故双曲线方程为C:x2  1…………4分
  1 4
a2 b2
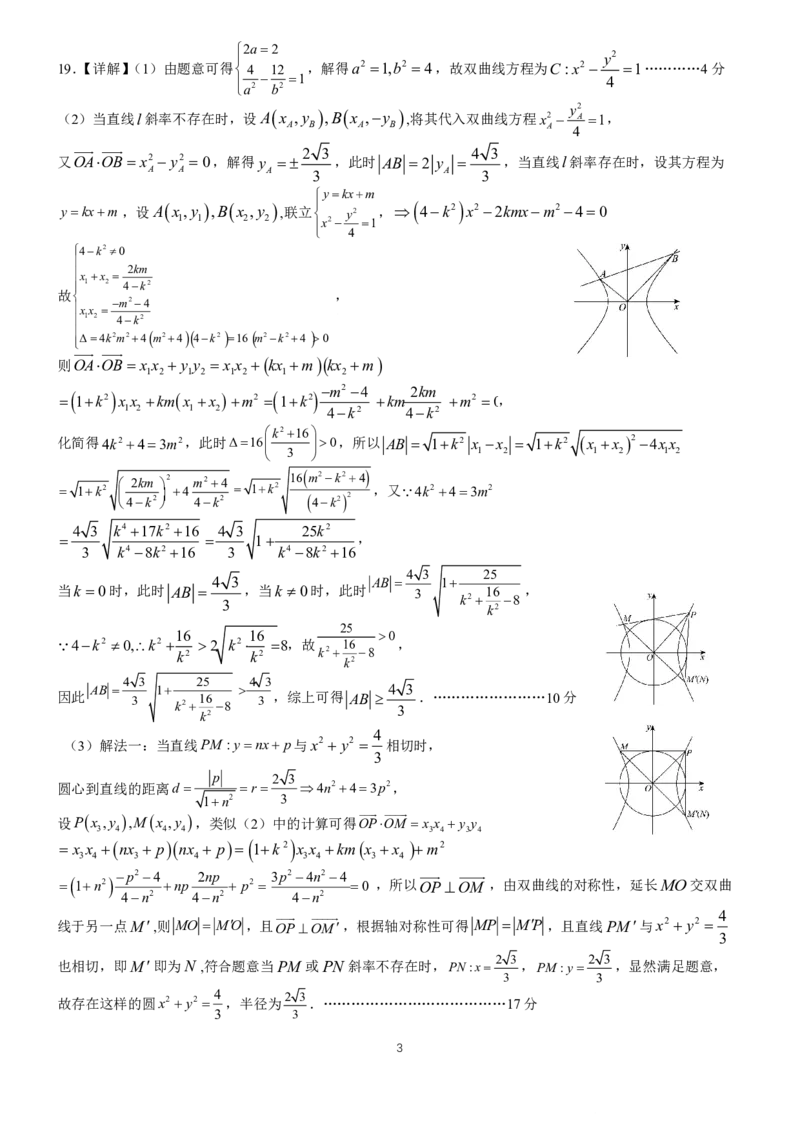
（2）当直线l斜率不存在时，设A  x ,y  ,B  x ,y  ,将其代入双曲线方程x2  y A 2 1，
A B A B A 4
 
2 3 4 3
又OAOB  x2  y2  0，解得y  ，此时 AB 2 y  ，当直线l斜率存在时，设其方程为
A A A 3 A 3
ykxm
ykxm，设A  x ,y  ,B  x ,y  ,联立   y2 ，  4k2 x22kmxm240
1 1 2 2 x2 1
 4
4k20

 x x  2km
 1 2 4k2
故 ，
m24
xx 
 1 2 4k2


Δ4k2m24  m24  4k2 16  m2k24 0
 
则OAOB  x x  y y  x x   kx m  kx m 
1 2 1 2 1 2 1 2
  1k2  x x km  x x  m2   1k2  m2 4 km 2km m2 0，
1 2 1 2 4k2 4k2
k216
化简得4k2 43m2，此时Δ16 0，所以 AB  1k2 x x  1k2  x x 24xx
 3  1 2 1 2 1 2
 1k2   4 2  km k2    2 4 m 4 2 k2 4  1k2 16   m 4 2   k k 2 2 2 4  ，又 4k243m2
4 3 k4 17k2 16 4 3 25k2
  1 ，
3 k4 8k2 16 3 k4 8k2 16
4 3 25
4 3 AB  1
当k 0时，此时 AB  ，当k  0时，此时 3 16 ，
k2 8
3
k2
25
16 16 0
4k2 0,k2  2 k2 8，故 16 ，
k2 k2 k2 8
k2
4 3 25 4 3
AB  1  4 3
因此 3 16 3 ，综上可得 AB  ．……………………10分
k2 8
3
k2
4
（3）解法一：当直线PM :ynx p与x2  y2  相切时，
3
p 2 3
圆心到直线的距离d  r 4n243p2，
1n2 3
 
设Px ,y ,Mx ,y ，类似（2）中的计算可得OPOM x x y y
3 4 4 4 3 4 3 4
 x x  nx  p  nx  p   1k2 x x km  x x m2
3 4 3 4 3 4 3 4
  1n2 p24 np 2np  p2  3p24n24 0 ，所以O  P  O  M  ，由双曲线的对称性，延长MO交双曲
4n2 4n2 4n2
  4
线于另一点M,则 MO  MO ，且OPOM，根据轴对称性可得 MP  MP ，且直线PM与x2  y2 
3
2 3 2 3
也相切，即M即为N ,符合题意当PM 或PN 斜率不存在时，PN:x ，PM:y ，显然满足题意，
3 3
故存在这样的圆x2 y2  4 ，半径为 2 3 ．…………………………………17分
3 3
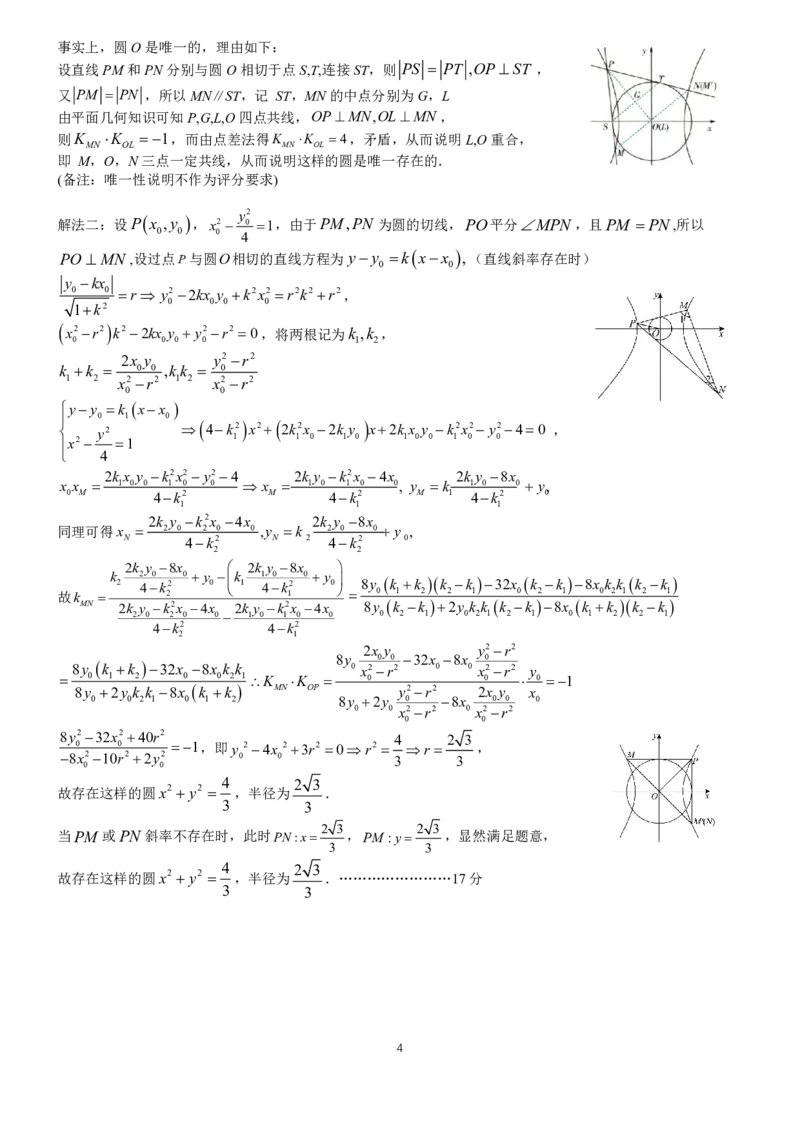
3事实上，圆O是唯一的，理由如下：
设直线PM和PN分别与圆O相切于点S,T,连接ST，则 PS  PT ,OP ST ，
又 PM  PN ，所以MN∥ST，记 ST，MN的中点分别为G，L
由平面几何知识可知P,G,L,O四点共线，OPMN,OLMN ，
则K K 1，而由点差法得K K 4，矛盾，从而说明L,O重合，
MN OL MN OL
即 M，O，N三点一定共线，从而说明这样的圆是唯一存在的．
(备注：唯一性说明不作为评分要求)
 
y2
解法二：设P x ,y ，x2  0 1，由于PM,PN 为圆的切线，PO平分MPN ，且PM  PN,所以
0 0 0 4
PO  MN ,设过点P与圆O相切的直线方程为 y y k  xx  ,（直线斜率存在时）
0 0
y kx
0 0 r y22kx y k2x2 r2k2r2，
0 0 0 0
1k2
 x2 r2 k2 2kx y  y2 r2 0，将两根记为k ,k ，
0 0 0 0 1 2
2x y y2 r2
k k  0 0 ,k k  0
1 2 x2 r2 1 2 x2 r2
0 0
yy k xx 
 
x2 
0 y2

1
1
0   4k
1
2 x2  2k
1
2x
0
2k
1
y
0
 x2k
1
x
0
y
0
k
1
2x
0
2 y
0
240 ，
 4
2k x y k2x2  y2 4 2k y k2x 4x 2k y 8x
x x  1 0 0 1 0 0  x  1 0 1 0 0, y k 1 0 0  y,
0 M 4k2 M 4k2 M 1 4k2 0
1 1 1
2k y k2x 4x 2k y 8x
同理可得x  2 0 2 0 0 ,y k 2 0 0 y ,
N 4k2 N 2 4k2 0
2 2
2k y 8x  2k y 8x 
故k  k 2 2 4 0 k 2 2 0 y 0   k 1 1 4 0 k 1 2 0 y 0    8y 0 k 1 k 2 k 2 k 1 32x 0 k 2 k 1 8x 0 k 2 k 1 k 2 k 1 
MN 2k y k2x 4x 2k y k2x 4x 8y k k 2y k k k k 8x k k k k 
2 0 2 0 0  1 0 1 0 0 0 2 1 0 2 1 2 1 0 1 2 2 1
4k2 4k2
2 1
2x y y2r2
8y 0 0 32x 8x 0
8y  k k 32x 8x k k 0 x2r2 0 0 x2r2 y
 0 1 2 0 0 2 1K K  0 0  0 1
8y 2y k k 8x  k k  MN OP y2r2 2x y x
0 0 2 1 0 1 2 8y 2y 0 8x 0 0 0
0 0 x2r2 0 x2r2
0 0
8y2 32x2 40r2
4 2 3
0 0 1，即y 24x 23r2 0r2  r  ，
8x2 10r2 2y2 0 0 3 3
0 0
4 2 3
故存在这样的圆x2  y2  ，半径为 ．
3 3
2 3 2 3
当PM 或PN 斜率不存在时，此时PN:x ，PM :y ，显然满足题意，
3 3
4 2 3
故存在这样的圆x2  y2  ，半径为 ．……………………17分
3 3
4