2025届广西南宁市普通高中毕业班摸底测试数学+答案_2024-2025高三（6-6月题库）_2024年09月试卷_0922广西南宁市2024-2025学年高三上学期普通高中毕业班摸底测试

{{##{{QQQQAABBaYYYCAEg4owgAgo4AkIJZJAACAZR4g7CAAwwGXK6CCwgoMQQkkJBECSCJUAgYGgGxVBAEFAuEAoxAjwAJBNAAQBNIAA=B}A#}A=}#}{{##{{QQQQAABBaYYYCAEg4owgAgo4AkIJZJAACAZR4g7CAAwwGXK6CCwgoMQQkkJBECSCJUAgYGgGxVBAEFAuEAoxAjwAJBNAAQBNIAA=B}A#}A=}#}{{##{{QQQQAABBaYYYCAEg4owgAgo4AkIJZJAACAZR4g7CAAwwGXK6CCwgoMQQkkJBECSCJUAgYGgGxVBAEFAuEAoxAjwAJBNAAQBNIAA=B}A#}A=}#}{{##{{QQQQAABBaYYYCAEg4owgAgo4AkIJZJAACAZR4g7CAAwwGXK6CCwgoMQQkkJBECSCJUAgYGgGxVBAEFAuEAoxAjwAJBNAAQBNIAA=B}A#}A=}#}南宁市 2025 届普通高中毕业班摸底测试参考答案（含评分细则） （数 学） 一、选择题：本题共 8 小题，每小题 5 分，共 40 分。在每小题给出的四个 选项中，只有一项是符合题目要求的。 题号 1 2 3 4 5 6 7 8 答案 D B A D B C A C 二选择题：本大题共 3 小题，每小题 6 分，共 18 分。在每小题给出的选项 中，有多项符合题目要求。全部选对的得 6 分，有选错的得 0 分。有两个 正确选项的仅选其中一个给 3 分；有三个正确选项的仅选其中一个给 2 分， 仅选其中两个给 4 分。 题号 9 10 11 答案 AD BC BCD 1.D z i(17i) 7i，则z 7i，故选 D． 2.B 当x 1时x3  x2，所以 p为真命题；当x 0时x4 0，所以q为假命题， 则q是真命题,故选 B． 3.A 由 a2b  2ab 2得a2 4a b+4b2  4,4a2 4a b+b2  4，两式相减得， 1 a  b 1，所以14a b+44，则a b  ，故选 A． 4 4.D 成绩在[70,80)上频率为110(0.010.020.020.03)0.2，所以成绩在 [70,80)上有0.25010人，成绩在[50,60),[60,70),[80,90),[90,100]的人数分别为 5， 10，15，10 人，所以成绩在[80,90)上的人数最多，A 正确；成绩不低于 70 分的学生所占比例为110(0.010.02)0.7，B 正确；50 名学生成绩的平均分 为x 550.1650.2750.2850.3950.2 78，成绩的中位数为 80 分， 所以 50 名学生成绩的平均分小于其成绩的中位数，C 正确；50 名学生成绩 的极差在[30,50]上，不一定为 50，D 错误，故选 D ． 1 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}y y y y 5.B 设M(x,y)(y 0)，则k  ,k  ,由k .k   2,整理得 AM x1 BM x1 AM BM x1 x1 y2 x2  1(y 0)，故选 B ． 2 1 x1 6.C 由题可 f'(x) 1 .m ,当x(0,1)时，f '(x)0;当x(1,)时，f '(x) 0, mx x 所以 f(x)在（0，1）上递减，在（1，）上递增，则 f(x) =f(1)=1-lnm0， min 所以 m≤e，又x＞0，mx＞0,即 m＞0.则 0＜m≤e,故选 C. 7.A 由正三棱台ABC  ABC 的侧面积为 6 得，等腰梯形ABB A 的面积为 2， 1 1 1 1 1 1 AB AB 由 (AB AB ) 2( 1 1)2  2得，AB 2 AB2 1，解得 2 1 1 2 1 1 1 1 AB 1，则AB 3AB 3，将正三棱台ABC  ABC 补成正三棱 1 1 1 1 1 1 1 PA 1 2 锥P ABC，如图所示，则 1  .所以PA  ，则 PA  2 3 1 2 1 3 PA 2，过 P 作PO平面 ABC，则 O 为△ABC 的中心，所以 2 3 2AO   2 3，则AO  3，易知PAO为AA 与平面 ABC 所成的角， sin60 1 AO 3 6 在Rt△PAO中，cosPAO    ，故选 A． PA 3 3 2 2 x2 (2x)2 2x2 4x4 8.C 因为g(x) g(2x)     2， x2 2x2 (2x)2 2(2x)2 x2 2x2 所以y  g(x)关于点(1,1)对称.要使 AB  BC ，则B(1,1),所以将B(1,1)代入 f(x)  ax得a 1,当a 1时 f(x)  x关于点(1,1)对称,显然 AB  BC ,故选 C ． sinx,x[2kπ,2kπ] π 9.AD f(x)  sinx   ,(kZ),g(x) sin(2x ) cos2x， sinx,x[2kππ,2kπ] 2 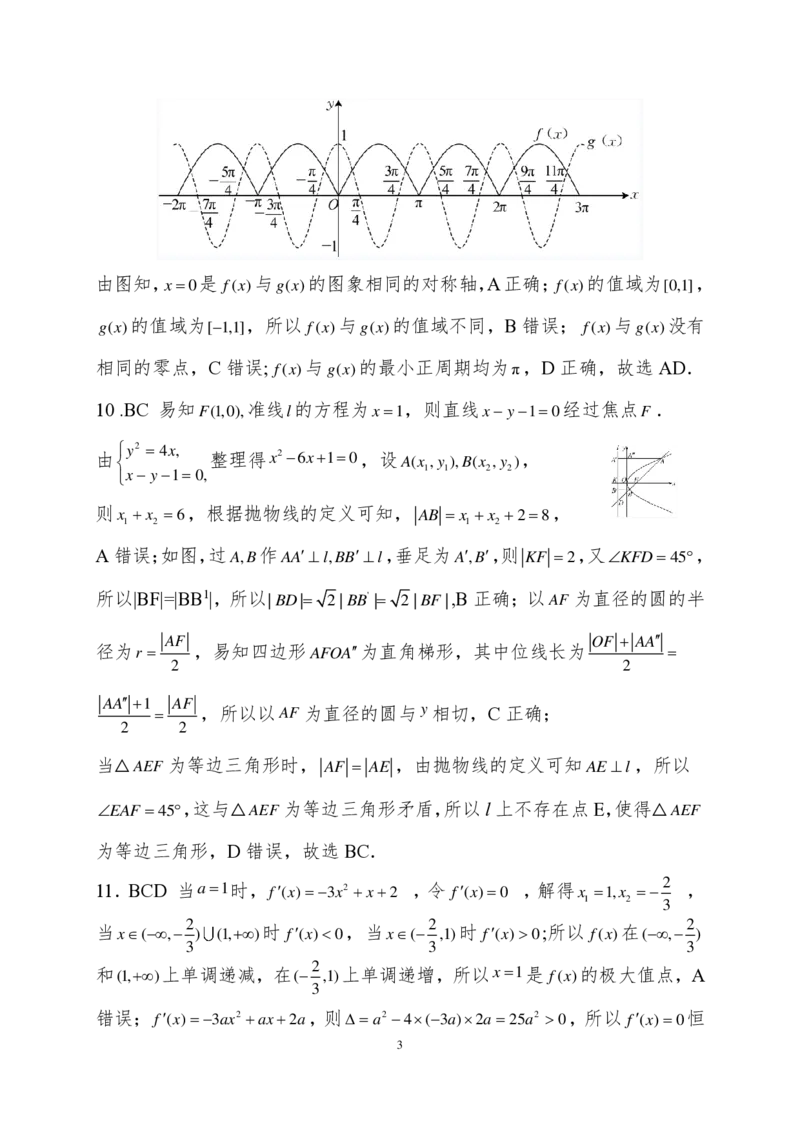在同一坐标系中作出 f(x)与g(x)的图象，如图所示， 2 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}由图知，x 0是 f(x)与g(x)的图象相同的对称轴，A正确；f(x)的值域为[0,1]， g(x)的值域为[1,1]，所以 f(x)与g(x)的值域不同，B 错误； f(x)与g(x)没有 相同的零点，C 错误; f(x)与g(x)的最小正周期均为π，D 正确，故选 AD． 10 .BC 易知F(1,0),准线l的方程为x 1，则直线x y10经过焦点F ． y2  4x, 由  整理得x2 6x10，设A(x ,y ),B(x ,y )， x y1 0, 1 1 2 2 则x  x 6，根据抛物线的定义可知， AB  x x 28， 1 2 1 2 A 错误；如图，过A,B作AAl,BBl，垂足为A,B，则 KF 2，又KFD45， 所以|BF|=|BB1|，所以|BD| 2|BB' | 2|BF |,B 正确；以AF 为直径的圆的半 AF OF  AA 径为r  ，易知四边形AFOA为直角梯形，其中位线长为  2 2 AA 1 AF  ，所以以AF 为直径的圆与y相切，C 正确； 2 2 当△AEF 为等边三角形时， AF  AE ，由抛物线的定义可知AE l，所以 EAF 45，这与△AEF 为等边三角形矛盾，所以 l 上不存在点 E，使得△AEF 为等边三角形，D 错误，故选 BC． 2 11．BCD 当a1时，f (x)  3x2  x2 ，令 f(x) 0 ，解得x 1,x   ， 1 2 3 2 2 2 当x(, ) (1,)时 f(x)0，当x( ,1)时 f(x) 0;所以 f(x)在(, ) 3 3 3 2 和(1,)上单调递减，在( ,1)上单调递增，所以x1是 f(x)的极大值点，A 3 错误；f (x)  3ax2 ax2a，则  a2 4(3a)2a  25a2 0，所以 f(x) 0恒 3 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}有两个根，结合二次函数的图象可知，f(x)恒有两个相同的单调区间，B 正 2 确；由上得 f (x)  3ax2 ax2a  a(3x2)(x1)，当a0时 f(x)在(, )和 3 2 (1,)上单调递减，在( ,1)上单调递增，要使 f(x)有三个零点，则 3  2 22 f( )   ab  0,   3 27 3a 22 3 b 22  解 b a,即   ； 3a 2 27 2 a 27  f(1)  b  0,  2 2 2 当a0时， f(x)在(, )和(1,)上单调递增，在( ,1)上单调递减， 3 3  2 22 f( )   ab  0,   3 27 22 3 3 b 22 要使 f(x)有三个零点，则  解 a b  a,即   . 3a 27 2 2 a 27  f(1)  b  0,  2 b 综上可知使得 f(x)有三个零点， 可取得的整数为﹣1，0，C 正确； a 1 设g(x)  f (x)  3ax2 ax2a，则g(x)  6axa，令g(x) 0得x  6 1 1 因为g(x)  6axa的零点为曲线 f(x)的对称中心的横坐标，所以点( , f( )) 6 6 为曲线y  f(x)的对称中心，D 正确，故选 BCD． 三、填空题：本题共 3 小题，每小题 5 分，共 15 分。 12．1 当n1得a a a ，又a  2,a 1,a  3得321，解得2. 3 1 2 1 2 3 则a  2a a ,a  2a a  213 5,a  2a a  2(3)51． n2 n n1 4 2 3 5 3 4 3 tan sincos 13． 由  2得  2,所以sincos2cossin. 5 tan cossin 1 2 则sin() sincoscossincossin  ，所以sincos  . 5 5 3 所以sin() sincoscossin  ． 5 14．① 24 （2 分） ② 216 （3 分） 若区域 A,B,C,D 涂 2 种颜色，区域 E,F,G,H 涂另外 2 种颜色，则AC,BD,EG,FH 同色，先选两种颜色涂 A,B,C,D 区域，则有C2A2种涂法，区域 E,F,G,H 有A2种涂法，故有C2A2A2 24种涂 4 2 2 4 2 2 4 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}法．区域 A,B,C,D 涂 4 种颜色有A4 24种涂法，不妨设区域 A,B,C,D 分别 4 涂a,b,c,d 颜色,则区域 E,F,G,H 也涂这 4 种颜色有(a,b,c,d),(a,d,b,c),(a,d,c,b), (c,d,a,b), (c,a,b,d), (c,b,a,d), (d,a,b,c), (d,a,c,b), (d,b,a,c),有 9 种涂法，共有 249216种涂法. 三、解答题：共 77 分，解答应写出文字说明、证明过程或演算步骤. 15.(本题 13 分) 设锐角△ABC 的内角 A,B,C 的对边分别为 a,b,c. 已知 2 bcsin2A=b2+c2－a2 . (1)求 A ;(2)若 a=2 2 ,且 2 c cosB=a sinC 求△ABC 的 面积. 解: (1) 由 2 bcsin2A=b2+c2－a2得 2 2 bcsinAcosA=b2+c2－a2……1 分 【备注 1】正确写出应用二倍角公式给 1 分。 𝑏2+𝑐2−𝑎2 即 √2sin𝐴cos𝐴 = = cos𝐴 …………………………….…1 分 2𝑏𝑐 【备注 2】正确写出或体现应用余弦定理公式给 1 分。 √2 在锐角△ABC 中 cosA≠0,所以sin𝐴 = ………………….…….....1 分(3 分） 2 √2 【备注 3】见“sin𝐴 = ”给 1 分 2 𝜋 𝜋 又0 < 𝐴 < ,所以𝐴 = . …………………………………………...2 分(5 分) 2 4 𝜋 【备注 4】见“𝐴 = ”给 2 分 4 (2) 由√2𝑐cos𝐵 = 𝑎sin𝐶及正弦定理得√2sin𝐶cos𝐵 = sin𝐴sin𝐶….1 分 √2 1 又 sinA≠0 所以√2cos𝐵 = sin𝐴 = 所以cos𝐵 = .………..…..….1 分 2 2 1 【备注 5】见“cos𝐵 = ”给 1 分. 2 𝜋 𝜋 又 0 < 𝐵 < ,所以𝐵 = ………………………………………….2 分(9 分) 2 3 𝜋 【备注 6】见“𝐵 = ”给 2 分 3 𝜋 𝜋 5𝜋 5𝜋 √6+√2 则𝐶 = 𝜋 − − = , 所以sin𝐶 = sin = …………...…1 分(10 分) 4 3 12 12 4 5 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}√3 𝑎sin𝐵 2√2× 由正弦定理得 𝑏 = = 2 = 2√3 ……………...…….…1 分(11 分) sin𝐴 √2 2 【备注 7】另解：写出“c  6  2 ”给 1 分。 1 1 √6+√2 故𝛥𝐴𝐵𝐶面积为 𝑎𝑏sin𝐶 = × 2√2× 2√3× = 3 + √3. …..2 分(13 分) 2 2 4 【备注8】结果正确即可给2分，若结果错误但正确写出面积公式可给1分。 【备注 9】无其他解答过程，只正确写出正弦定理、余弦定理公式各给 1 分。 16. (本题15分)已知函数f(x)=(4x+1)ex , 曲线y=f(x)在(0,f(0))处的切线为直线 l. (1)求直线 l 的方程; (2)求函数 f(x)在闭区间[－2,1]上的最值. 解: (1)依题意,求导得 f '(x)=(4x+5)ex…………………….…......…2 分(2 分) 【备注 1】求导结果正确给 2 分 f(0)= e0 =1………………………………….…………..………...…1 分 则𝑓′(0) = 5𝑒0 = 5…………………………………………………1 分(4 分) 【备注 2】若不写“f(0)= e0 =1，则𝑓′(0) = 5𝑒0 = 5”;只正确写出切点坐标 (0,1)也给这 1 分。 所以直线 l 的方程为 y=5x+1………………………………….….2 分(6 分) 【备注 3】直线方程结果正确给 2 分 (2)由(1)可知 f '(x)=(4x+5)ex 5 5 当x   时 f '(x) 0，则 f(x)在( ,)上单调递增；………1 分 4 4 5 5 当x   时 f '(x)0，则 f(x)在(, )上单调递减；………1 分(8 分) 4 4 5 5 【备注 4】正确写出“在x 时 f(x)单调递增”、“ 在x 时 f(x)在上单 4 4 5 5 5 5 调递减”给 1 分;写成闭区间[ ,)、(, ],[ ,1]、[2, ]也正确。 4 4 4 4 因为 f( 5 )  4e  5 4, f(2)  7e2, f(1) 5e………………………3 分(11 分) 4 6 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}【备注 5】正确写出结果,每对一个给 1 分. 则 f(x)在闭区间[-2,1]上最大值为 5e, …………………..……2 分 5 最小值为4e  4.…………………………………………………2 分(15 分) 【备注 6】正确写出结果,每对一个给 2 分. 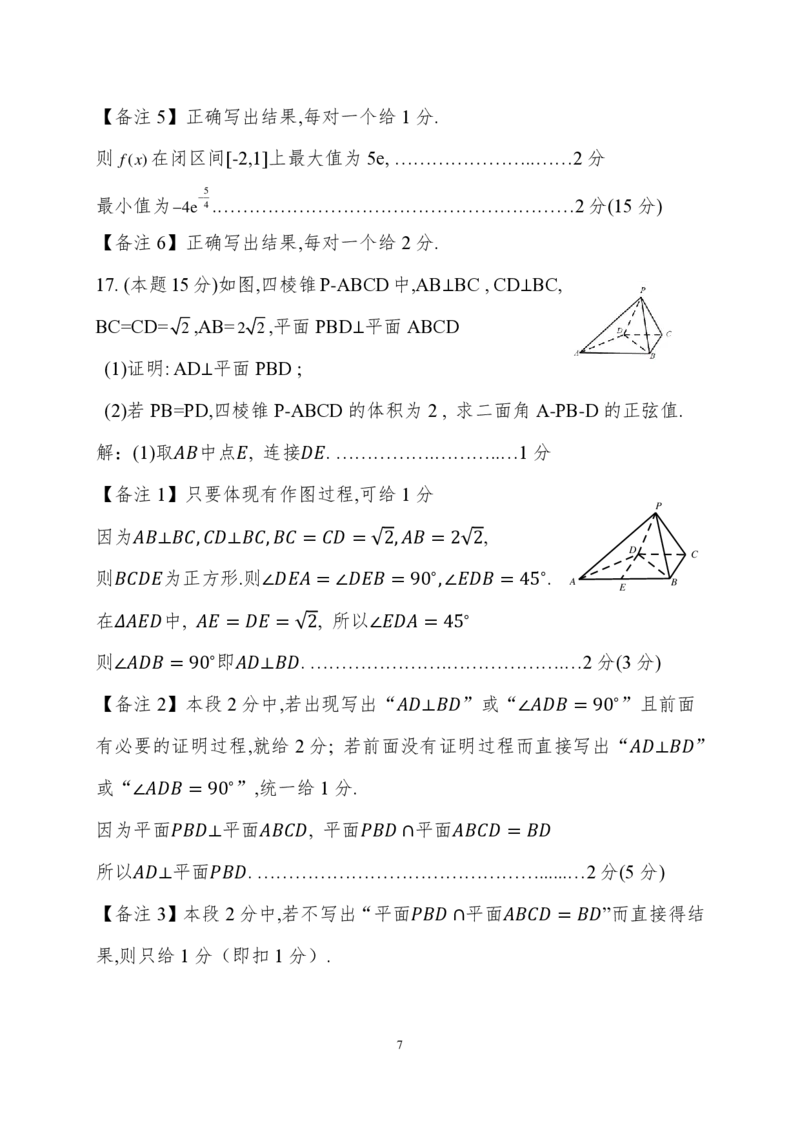17. (本题15分)如图,四棱锥P-ABCD中,AB⊥BC , CD⊥BC, BC=CD= 2 ,AB=2 2,平面 PBD⊥平面 ABCD (1)证明: AD⊥平面 PBD ; (2)若 PB=PD,四棱锥 P-ABCD 的体积为 2 , 求二面角 A-PB-D 的正弦值. 解：(1)取𝐴𝐵中点𝐸, 连接𝐷𝐸. …………….………..…1 分 【备注 1】只要体现有作图过程,可给 1 分 P 因为𝐴𝐵⟂𝐵𝐶,𝐶𝐷⟂𝐵𝐶,𝐵𝐶 = 𝐶𝐷 = √2,𝐴𝐵 = 2√2, D C 则𝐵𝐶𝐷𝐸为正方形.则∠𝐷𝐸𝐴 = ∠𝐷𝐸𝐵 = 90∘,∠𝐸𝐷𝐵 = 45∘. A B E 在𝛥𝐴𝐸𝐷中, 𝐴𝐸 = 𝐷𝐸 = √2, 所以∠𝐸𝐷𝐴 = 45∘ 则∠𝐴𝐷𝐵 = 90∘即𝐴𝐷⟂𝐵𝐷. ………………….……………….…2 分(3 分) 【备注 2】本段 2 分中,若出现写出“𝐴𝐷⟂𝐵𝐷”或“∠𝐴𝐷𝐵 = 90∘”且前面 有必要的证明过程,就给 2 分; 若前面没有证明过程而直接写出“𝐴𝐷⟂𝐵𝐷” 或“∠𝐴𝐷𝐵 = 90∘”,统一给 1 分. 因为平面𝑃𝐵𝐷⟂平面𝐴𝐵𝐶𝐷, 平面𝑃𝐵𝐷 ∩平面𝐴𝐵𝐶𝐷 = 𝐵𝐷 所以𝐴𝐷⟂平面𝑃𝐵𝐷. ………………………………………......…2 分(5 分) 【备注 3】本段 2 分中,若不写出“平面𝑃𝐵𝐷 ∩平面𝐴𝐵𝐶𝐷 = 𝐵𝐷”而直接得结 果,则只给 1 分（即扣 1 分）. 7 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}(2)连接𝐶𝐸, 设𝐶𝐸 ∩ 𝐵𝐷 = 𝑂, 则𝑂为𝐵𝐷的中点, 连接𝑃𝑂. 因为𝑃𝐵 = 𝑃𝐷, 所以𝑃𝑂⟂𝐵𝐷. ………………..…..1 分(6 分) 【备注 4】见“𝑃𝑂⟂𝐵𝐷”给 1 分。 面 𝑃𝐵𝐷⟂面𝐴𝐵𝐶𝐷, 面𝑃𝐵𝐷 ∩面𝐴𝐵𝐶𝐷 = 𝐵𝐷,𝑃𝑂 ⊂面𝑃𝐵𝐷, 所以𝑃𝑂⟂平面𝐴𝐵𝐶𝐷. ……………………………………………1 分(7 分) 【备注 5】见“𝑃𝑂⟂平面𝐴𝐵𝐶𝐷”给 1 分。 1 1 由四棱锥𝑃 − 𝐴𝐵𝐶𝐷体积为 2 , 则 × (𝐴𝐵 + 𝐶𝐷) ⋅ 𝐵𝐶 ⋅ 𝑃𝑂 = 2 3 2 1 1 即 × × 3√2 × √2 × 𝑃𝑂 = 2, 解得𝑃𝑂 = 2. …………………2 分(9 分) 3 2 【备注 6】见结果正确“𝑃𝑂 = 2”给 2 分。 由 OE∥AD 可知𝑂𝐸,𝑂𝐵,𝑂𝑃两两垂直, 以𝑂为原点, 𝑂𝐸,𝑂𝐵,𝑂𝑃所在直线 分别为𝑥轴、𝑦轴、𝑧轴建立空间直角坐标系𝑂 − 𝑥𝑦𝑧, ….…….1 分(10 分) 【备注 7】见建系结果正确或图中正确标出建系结果，即可给 1 分。 则𝐴(2 , −1 , 0),𝐸(1 , 0 , 0),𝐵(0 , 1 , 0),𝑃(0 , 0 , 2), 𝑃⃗⃗⃗⃗𝐴⃗ = (2 , −1 , −2),𝐴⃗⃗⃗⃗𝐵⃗ = (−2, 2,0),𝑂⃗⃗⃗⃗𝐸⃗ = (1 , 0 , 0). 设平面𝑃𝐴𝐵的法向量为𝑚 = (𝑥 , 𝑦 , 𝑧), 𝑃⃗⃗⃗⃗𝐴⃗ ⋅ 𝑚 = 0, 2𝑥 − 𝑦 − 2𝑧 = 0, 由{ 得{ 令𝑥 = 2, 则𝑚 = (2 , 2 , 1) 𝐴⃗⃗⃗⃗𝐵⃗ ⋅ 𝑚 = 0, −2𝑥 + 2𝑦 = 0, 由𝑂𝐸//𝐴𝐷可知, 𝑂𝐸⟂平面𝑃𝐵𝐷, 所以𝑂⃗⃗⃗⃗𝐸⃗ 是平面𝑃𝐵𝐷的法向量, 记为𝑛 = 𝑂⃗⃗⃗⃗𝐸⃗ = (1 , 0 , 0) ………………………………………..……3 分(13 分) 【备注 8】本段 3 分,求两个法向量,对一个给 2 分，对两个给 3 分;若法向量 𝑃⃗⃗⃗⃗𝐴⃗ ⋅ 𝑚 = 0, 都不对，但写有数量积等于 0 如：“{ ” (或外积法)，表示方法 𝐴⃗⃗⃗⃗𝐵⃗ ⋅ 𝑚 = 0, 正确，统一给 1 分 8 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}则cos⟨𝑚 , 𝑛⟩ = 𝑚⋅𝑛 = 2 ,故二面角𝐴 − 𝑃𝐵 − 𝐷正弦值为 √5 . ……....2分(15分) |𝑚|⋅|𝑛| 3 3 【备注 9】结果正确即可给 2 分;若结果错误,但前面能正确写出求夹角原始 公式“cos⟨𝑚 , 𝑛⟩ = 𝑚⋅𝑛 ” 可给 1 分. |𝑚|⋅|𝑛| 其他解法如下： 第一问解法二： 第二问解法二： 9 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}第二问解法三： 第二问解法四： 第二问解法五： 10 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}第二问解法六 18.(本题 17 分) 我省某市为吸引游客, 推出免费门票项目. 该市设置自然 风光类、历史文化类、特色体验类三个免费票抽奖机, 自然风光类抽中的概 1 1 率为 , 历史文化类、特色体验类抽中的概率均为 ,这三类抽奖之间互不影响. 3 2 规定凡在该市的景区游玩的游客, 每位游客可在每个抽奖机中至多抽奖一 次，每次抽奖至多抽中一个免费票景点. (1)若甲游客在三个抽奖机中各抽奖一次, 设𝑋表示甲获得免费票景点个数, 求𝑋的分布列和数学期望； (2)乙游客从这三个抽奖机中随机选取两个抽奖, 已知乙抽中 (至少抽中一 个), 求乙在自然风光类、特色体验类抽奖机中抽中的概率. 解: (1) 𝑋表示甲获得免费票景点个数, 则𝑋 = 0,1,2,3, …………..……1 分 11 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}1 1 1 1 则 𝑃(𝑋 = 0) = (1 − ) × (1 − ) × (1 − ) = ; ………………………1 分 3 2 2 6 𝑃(𝑋 = 1) = 1 × (1 − 1 ) × (1 − 1 ) + (1 − 1 ) × 𝐶1(1 − 1 ) × 1 = 5 . …..1 分 2 3 2 2 3 2 2 12 2 𝑃(𝑋 = 2) = 1 × 𝐶1 × 1 × (1 − 1 ) + (1 − 1 ) × ( 1 ) = 1 . ………………1 分 2 3 2 2 3 2 3 1 1 1 1 𝑃(𝑋 = 3) = × × = …………………………………….………1 分(5 分) 3 2 2 12 故 X 的分布列为 X 0 1 2 3 1 5 1 1 P 6 12 3 12 【备注 1】若仅给出分布列而没有前面的求解过程：表中数字全对时本 5 分 段共给 4 分（即扣掉过程分 1 分）；当表中概率数字不全对时，若表头第一 行数字全对给 1 分，第二行每个概率值对一个给 1 分（共不超过 3 分） 1 5 1 1 4 𝐸(𝑋) = 0 × + 1 × + 2 × + 3 × = .. …………...........……3 分(8 分) 6 12 3 12 3 【备注 2】体现数学期望公式（乘积和，至少写有两项）给 1 分,结果正确 给2分；如果没有过程只写正确结果E(X)=4/3给2分(扣求数学期望过程分). （2）设“乙抽中”为事件𝑀, “乙在自然风光类、特色体验类抽奖机中抽 奖与抽中”分别为事件 𝑁 ,𝑀 , “乙在自然风光类、历史文化类抽奖机中抽 1 1 奖与抽中”分别为事件𝑁 ,𝑀 , “乙在历史文化类、特色体验类抽奖机中抽 2 2 奖与抽中”分别为事件𝑁 ,𝑀 .. ………………………………..….…1 分（9 分） 3 3 【备注 3】体现至少设出一个事件过程，可给 1 分。 1 1 1 2 则𝑃(𝑀 ) = 𝑃(𝑁 )𝑃(𝑀 |𝑁 ) = × [1 − (1 − )(1 − )] = . …………1 分 1 1 1 1 3 3 2 9 1 1 1 2 𝑃(𝑀 ) = 𝑃(𝑁 )𝑃(𝑀 |𝑁 ) = × [1 − (1 − )(1 − )] = .. ……………1 分 2 2 2 2 3 3 2 9 1 1 1 1 𝑃(𝑀 ) = 𝑃(𝑁 )𝑃(𝑀 |𝑁 ) = × [1 − (1 − )(1 − )] = ….……1 分(12 分) 3 3 3 3 3 2 2 4 因事件 M ,M ,M 两两互斥, 1 2 3 12 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}所以𝑃(𝑀) = 𝑃(𝑀 ∪ 𝑀 ∪ 𝑀 ) = 𝑃(𝑀 ) + 𝑃(𝑀 )+ 𝑃(𝑀 ). ……1 分 1 2 3 1 2 3 【备注 4】正确写出求互斥事件概率公式给 1 分. 2 2 1 25 = + + = ..…………………………………………………….1 分(14 分) 9 9 4 36 【备注 5】结果正确给 1 分 𝑃(𝑀 𝑀) 𝑃(𝑁 )𝑃(𝑀 |𝑁 ) 2 36 8 则 𝑃(𝑀 |𝑀) = 1 = 1 1 1 . = × = ………..….…2分(16分) 1 𝑃(𝑀) 𝑃(𝑀) 9 25 25 【备注 6】计算结果正确,给 1 分；若结果不对，但写出几何条件公式 𝑃(𝑀 𝑀) “𝑃(𝑀 |𝑀) = 1 ”给 1 分. 1 𝑃(𝑀) 8 故乙在自然风光类、特色体验类抽奖机中抽中的概率为 . ………1分(17分) 25 8 【备注 7】作答正确给 1 分,若写出“ 为所求”也算作答正确. 25 𝑥2 𝑦2 3 19. (本题 17 分) 已知椭圆𝐶: + = 1(𝑎 > 𝑏 > 0)经过点（b, b)𝐴 ,𝐴 𝑎2 𝑏2 2 1 2 为𝐶的左、右顶点, 𝑀,𝑁为𝐶上不同于𝐴 ,𝐴 的两动点.若直线𝐴 𝑀斜率与直线 1 2 1 7 𝐴 𝑁斜率比值恒为常数 , 按下面方法构造数列 {𝑏 }:𝐶的短半轴长为𝑏 时, 2 𝑛 𝑛 5 直线𝑀𝑁与𝑥轴交于点𝑄 (−𝑏 , 0). 𝑛 𝑛+1 (1)求椭圆𝐶的离心率; (2)证明: 数列{𝑏 }是等比数列; (3)设顶点𝐴 到直线 𝑛 1 5 𝑀𝑁的最大距离为𝑑, 证明: 𝑑 ⩽ 𝑏 . 1 3 解: (1)由椭圆𝐶经过点(−𝑏 , − √3 𝑏)得 𝑏2 + 3𝑏2 = 1,故 𝑏2 = 1 . ………......1 分 2 𝑎2 4𝑏2 𝑎2 4 𝑏2 1 【备注 1】见“ = ”或“𝑎2 = 4𝑏2”或“𝑎 = 2𝑏”给 1 分。 𝑎2 4 𝑐2 𝑏2 √3 √3 则𝑒 = √ = √1 − = ,所以椭圆𝐶离心率为 . ………….......…2 分(3 分) 𝑎2 𝑎2 2 2 【备注 2】见结果正确给 2 分,若结果错误,但体现离心率公式正确给 1 分. (2)证明: 由(1)及题意可知𝐶: 𝑥2 + 𝑦2 = 1,𝐴 (−2𝑏 , 0),𝐴 (2𝑏 , 0)……1 分 4𝑏2 𝑏2 1 𝑛 2 𝑛 𝑛 𝑛 𝑥2 𝑦2 【备注 3】写出“ + = 1”给 1 分 4𝑏2 𝑏2 𝑛 𝑛 13 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}设𝑀(𝑥 , 𝑦 ),𝑁(𝑥 , 𝑦 ), 当直线𝑀𝑁斜率为 0 时𝑀,𝑁关于𝑦轴对称, 1 1 2 2 所以𝐴 𝑀斜率与𝐴 𝑁的斜率之商为﹣1.不合题意. ..…………….….1分(5分) 1 2 设𝑀𝑁方程为𝑥 = 𝑡𝑦 + 𝑚, …………………………………….……1 分 【备注 4】正确设出直线𝑀𝑁方程(可以其他形式)给 1 分. 因为𝑀𝑁不过顶点𝐴 ,𝐴 所以𝑚 ≠ ±2𝑏 . 1 2 𝑛 𝑥 = 𝑡𝑦 + 𝑚, 由{𝑥2 𝑦2 得(𝑡2 + 4)𝑦2 + 2𝑡𝑚𝑦 + 𝑚2 − 4𝑏2 = 0. + = 1, 𝑛 4𝑏2 𝑏2 𝑛 𝑛 则△= 4𝑡2𝑚2 − 4(𝑡2 + 4)(𝑚2 − 4𝑏2) = 16(𝑡2𝑏2 − 𝑚2 + 4𝑏2) > 0 𝑛 𝑛 𝑛 2𝑡𝑚 𝑚2−4𝑏2 𝑦 + 𝑦 = − ,𝑦 𝑦 = 𝑛. ……………………………..……1 分(7 分) 1 2 𝑡2+4 1 2 𝑡2+4 【备注 5】至少正确写出韦达定理中一个式子,给 1 分. 4𝑏2−𝑚2 所以𝑡𝑦 𝑦 = 𝑛 (𝑦 + 𝑦 )……………………………………..…1 分 1 2 1 2 2𝑚 【备注 6】写出“𝑦 + 𝑦 ”与“𝑦 𝑦 ”关系，给 1 分 1 2 1 2 则 𝑘 𝐴1𝑀 = 𝑦 1 ⋅ 𝑥 2 −2𝑏 𝑛. ………………………………………..….…1 分 𝑘 𝑥 +2𝑏 𝑦 𝐴2𝑁 1 𝑛 2 【备注 7】正确写出直线斜率公式给 1 分. (𝑡𝑦 + 𝑚 − 2𝑏 )𝑦 𝑡𝑦 𝑦 + (𝑚 − 2𝑏 )𝑦 2 𝑛 1 2 1 𝑛 1 = = (𝑡𝑦 + 𝑚 + 2𝑏 )𝑦 𝑡𝑦 𝑦 + (𝑚 + 2𝑏 )𝑦 1 𝑛 2 2 1 𝑛 2 4𝑏2 − 𝑚2 𝑛 (𝑦 + 𝑦 ) + (𝑚 − 2𝑏 )𝑦 2𝑚 1 2 𝑛 1 = 4𝑏2 − 𝑚2 𝑛 (𝑦 + 𝑦 ) + (𝑚 + 2𝑏 )𝑦 2𝑚 1 2 𝑛 2 2𝑏 −𝑚 (2𝑏 +𝑚)(𝑦 +𝑦 )−2𝑚𝑦 2𝑏 −𝑚 = 𝑛 ⋅ 𝑛 1 2 1 = 𝑛 . ……………………….…1 分(10 分) 2𝑏 +𝑚 (2𝑏 −𝑚)(𝑦 +𝑦 )+2𝑚𝑦 2𝑏 +𝑚 𝑛 𝑛 1 2 2 𝑛 【备注 8】见能化简到“ 𝑘 𝐴1𝑀 = 2𝑏 𝑛 −𝑚 ”或“ 𝑘 𝐴2𝑁 = 2𝑏 𝑛 +𝑚 ”并前面有必要的 𝑘 2𝑏 +𝑚 𝑘 2𝑏 −𝑚 𝐴2𝑁 𝑛 𝐴1𝑀 𝑛 化简过程才给 1 分. 7 1 = 所以𝑚 = − 𝑏 . ………………………………………………1 分(11 分) 𝑛 5 3 则直线𝑀𝑁方程为𝑥 = 𝑡𝑦 − 1 𝑏 ,即𝑀𝑁经过点(− 1 𝑏 , 0)…….….1 分 𝑛 𝑛 3 3 14 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}【备注 9】正确写出“𝑀𝑁经过点(− 1 𝑏 , 0)”给 1 分. 𝑛 3 因为𝑀𝑁与𝑥轴交于点𝑄 (−𝑏 , 0),所以−𝑏 = − 1 𝑏 , 𝑏 𝑛+1 = 1 . 𝑛 𝑛+1 𝑛+1 𝑛 3 𝑏 3 𝑛 1 所以数列{𝑏 }是以 为公比的等比数列. ………………………….....1分(13分) 𝑛 3 𝑛−1 1 (3) 证明: 由(2)可知, 𝑏 = ( ) 𝑏 . ………………………...….1 分(14 分) 𝑛 1 3 𝑛−1 1 所以{𝑏 }是递减数列,则𝑏 = ( ) 𝑏 ⩽ 𝑏 ……………………...1 分 𝑛 𝑛 1 1 3 𝑛−1 1 【备注 10】见“𝑏 = ( ) 𝑏 ⩽ 𝑏 ”给 1 分. 𝑛 1 1 3 顶点𝐴 (−2𝑏 , 0)到直线𝑀𝑁:𝑡𝑦 − 𝑥 − 1 𝑏 = 0距离为 1 𝑛 𝑛 3 1 𝑑 = |2𝑏 𝑛 − 3 𝑏 𝑛 | = 5𝑏 𝑛 ⩽ 5𝑏 𝑛,当𝑡 = 0时取等号; ……………........…1 分(16 分) √𝑡2+1 3√𝑡2+1 3 1 【备注 11】见“𝑑 = |2𝑏 𝑛 − 3 𝑏 𝑛 | ”或“𝑑 ⩽ 5𝑏 𝑛”给 1 分. √𝑡2+1 3 5 故𝑑 ⩽ 𝑏 . …………………........................................................…1 分(17 分) 1 3 15 {#{QQABTYiEogigAoAAARhCEwEYCEIQkBGCCYgGRFAMsAABwAFABAA=}#}