文档内容
2025 届新高三暑期效果联合测评
高三数学试卷
满分150分,考试用时120分钟
注意事项:
1. 答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码贴
在答题卡上的指定位置.
2. 选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.
写在试卷、草稿纸和答题卡上的非答题区域均无效.
3. 非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿
纸和答题卡上的非答题区域均无效.
4. 考试结束后,请将本试卷和答题卡一并上交.
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题所给的四个选项中,只有
一项是符合题目要求的)
1.已知集合 ,则 ( )
A. B.
C. D.
2.若复数 ,则 ( )
A.2 B.3 C. D.
3.若 ,则 ( )
A. B. C. D.
4.设 , , ,则( )
A. B. C. D.
5.在等差数列 中, , , ( )
学学科科网网((北北京京))股股份份有有限限公公司司A. B. C. D.
6.已知函数 ,则( )
A. 有三个极值点 B. 有三个零点
C.点 是曲线 的对称中心 D.直线 是曲线 的切线
7.若 的展开式中二项式系数和为64,则 ( )
A.3 B.4 C.5 D.6
8.已知正三棱锥 的侧棱与底面边长的比值为 ,则三棱锥 的侧棱与底面所成角的正弦
值为( )
A. B. C. D.
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求,全部选对得6分,部分选对的得部分分,有选错的得0分)
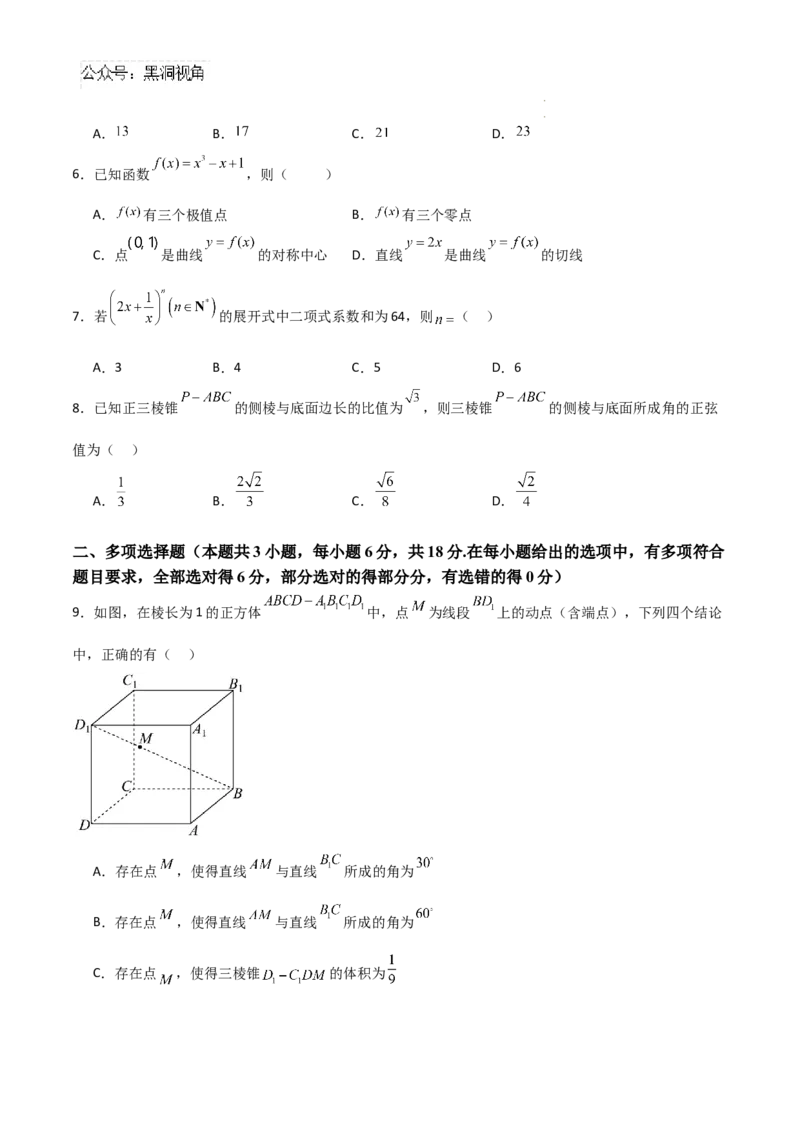
9.如图,在棱长为1的正方体 中,点 为线段 上的动点(含端点),下列四个结论
中,正确的有( )
A.存在点 ,使得直线 与直线 所成的角为
B.存在点 ,使得直线 与直线 所成的角为
C.存在点 ,使得三棱锥 的体积为
学学科科网网((北北京京))股股份份有有限限公公司司D.存在点 ,使得 平面
10.已知函数 , 的定义域均为R,且 , ,
,则下列说法正确的有( )
A. B. 为偶函数
C. 的周期为4 D.
11.已知圆 ,则( )
A.圆 与直线 必有两个交点
B.圆 上存在4个点到直线 的距离都等于1
C.圆 与圆 恰有三条公切线,则
D.动点 在直线 上,过点 向圆 引两条切线, 为切点,则四边形 面积最小值
为2
三、填空题(本大题共3小题,每小题5分,共15分)
12.某同学参加学校组织的数学知识竞赛,在4道四选一的单选题中,有3道有思路,有1道完全没有思
路,有思路的题每道做对的概率均为 ,没有思路的题只好任意猜一个答案.若从这4道题中任选2题作
答,则该同学2道题都做对的概率为 .
13.在 中, ,点D在线段 上, , , ,点M是 外接圆上任
意一点,则 最大值为 .
14.O为坐标原点,双曲线 的左焦点为 ,点P在E上,直线 与直线
学学科科网网((北北京京))股股份份有有限限公公司司相交于点M,若 ,则E的离心率为 .
四、解答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题13分)
已知正项数列 中, ,且 .
(1)求数列 的通项公式;
(2) ,证明: .
16.(本小题15分)
已知函数 .
(1)当 时,求曲线 在点 处的切线方程.
(2)若函数 有两个零点,求实数 的取值范围.
学学科科网网((北北京京))股股份份有有限限公公司司17.(本小题15分)
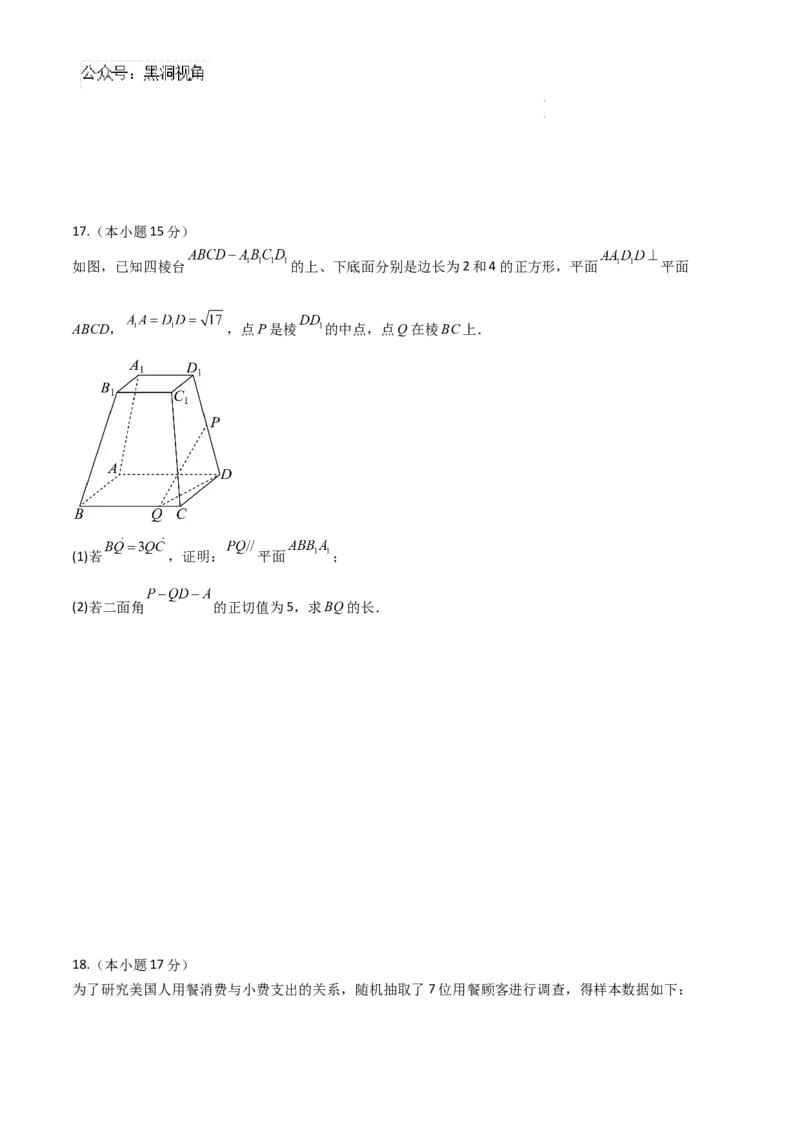
如图,已知四棱台 的上、下底面分别是边长为2和4的正方形,平面 平面
ABCD, ,点P是棱 的中点,点Q在棱BC上.
(1)若 ,证明: 平面 ;
(2)若二面角 的正切值为5,求BQ的长.
18.(本小题17分)
为了研究美国人用餐消费与小费支出的关系,随机抽取了7位用餐顾客进行调查,得样本数据如下:
学学科科网网((北北京京))股股份份有有限限公公司司消费(单元:美
32 40 50 86 63 100 133
元)
小费(单位:美
5 6 7 9 8 9 12
元)
相关公式: , .
参考数据: ,
.
(1)求小费 (单位:美元)关于消费 (单位:美元)的线性回归方程 (其中 的值精确到
0.001);
(2)试用(1)中的回归方程估计当消费200美元时,要付多少美元的小费(结果精确到整数)?
学学科科网网((北北京京))股股份份有有限限公公司司19.(本小题17分)
已知抛物线 : ,圆 : , 为坐标原点.
(1)若直线 : 分别与抛物线 相交于点A, ( 在B的左侧)、与圆 相交于点S,
(S在 的左侧),且 与 的面积相等,求出 的取值范围;
(2)已知 , , 是抛物线 上的三个点,且任意两点连线斜率都存在.其中 , 均与圆 相切,
请判断此时圆心 到直线 的距离是否为定值,如果是定值,请求出定值;若不是定值,请说明理由.
学学科科网网((北北京京))股股份份有有限限公公司司