2025届江西高三10月联考数学试卷+答案（金太阳）(1)_2024-2025高三（6-6月题库）_2024年10月试卷_10252025届江西省金太阳高三10月联考

高三数学试卷 注意事项： 1.答题前，考生务必将自己的姓名､考生号､考场号､座位号填写在答题卡上. 2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改 动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本 试卷上无效. 3.考试结束后，将本试卷和答题卡一并交回. 4.本试卷主要考试内容：集合与常用逻辑用语，不等式，函数与导数，三角函数，解三角形. 一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 1.已知全集U = A∪B={ 0,1,2,3,4,5 } ,A∩(  B )={ 1,3,5 } ，则集合B =（ ） U { } { } { } A. 1,3,5 B. 0,2,4 C.∅ D. 0,1,2,3,4,5 5π 5π 2.sin2 −cos2 =（ ） 12 12 1 3 1 3 A. B. C.− D.− 2 2 2 2 3.已知函数 f ( x ) 的定义域为R，且 f ( x+ y )− f ( x− y )=2f ( y ) ，则 f ( 0 )=（ ） A.0 B.1 C.2 D.−1 1 1 4.已知x>0,y >0，且 +2y =1，则2x+ 的最小值为（ ） x y A.2 B.4 C.6 D.8 5.设函数 f ( x )=ln ( x2 +1 ) +sinx+1，则曲线y = f ( x ) 在点 ( 0,1 ) 处的切线与两坐标轴所围成的三角形的 面积为（ ） 1 1 1 2 A. B. C. D. 2 3 6 3 6.把某种物体放在空气中，若该物体原来的温度是θ′C，空气的温度是θC，则tmin后该物体的温度 0 t θC满足θ=θ +(θ′−θ) e − 4.若θ 0 ,θ′不变，在t 1 min,t 2 min后该物体的温度分别为θ 1 C,θ 2 C，且 0 0 θ >θ，则下列结论正确的是（ ） 1 2 A.t >t 1 2 学科网（北京）股份有限公司B.t θ，则t >t ；若θ′<θ，则t θ，则t t 0 1 2 0 1 2 7.已知log m>1(m,n>0且m≠1,n≠1),m+n=e2，则（ ） n A.(m−n+1)e <1 B.(m−n+1)e >1 C.|m−n|e<1 D.|m−n|e>1 8.在ABC中，AB=4,BC =6,∠ABC =90，点P在ABC内部，且∠BPC =90,AP=2，记 ∠ABP=α，则tan2α=（ ） 3 2 4 3 A. B. C. D. 2 3 3 4 二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目 要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. π  π  π  9.已知命题 p:∃x∈R,x− x > x2；命题q:∀α∈  ,π,cos −α  =sin +α ，则（ ） 2  4  4  A. p是真命题 B. ¬p是真命题 C.q是真命题 D. ¬q是真命题  1 10.已知函数 f ( x )=cosx+ ，则（ ）  x ( ) A. f x 为偶函数 ( ) B. f x 的最大值为cos2 ( ) ( ) C. f x 在 1,2 上单调递减 ( ) ( ) D. f x 在 1,20 上有6个零点 1 11.已知函数 f ( x )= x3+bx2 +cx，下列结论正确的是（ ） 3 A.若x= x 是 f ( x ) 的极小值点，则 f ( x ) 在 (−∞,x ) 上单调递减 0 0 B.若x=b是 f ( x ) 的极大值点，则b<0且c<0 学科网（北京）股份有限公司( ) C.若c=3，且 f ( x ) 的极小值大于0，则b的取值范围为 −2,− 3 D.若c=−3b，且 f ( x ) 在 [ 0,3 ] 上的值域为 [ 0,9 ] ，则b的取值范围为 [−3,0 ] 三､填空题：本题共 3小题，每小题 5分，共 15分. 12.已知函数 f ( x )=sin ( x+ϕ) (0 ϕ<π)的图象关于y轴对称，则ϕ= __________. x2 +ax,x<0,  13.已知函数 f ( x )= x 的最小值为−1，则a=__________.  − ,x0  x+1 14.已知函数 f ( x )=sin ( x+ϕ)+1，若 f ( x )− f ( x ) =1，则 x −x 的最小值为__________. 1 2 1 2 四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤. 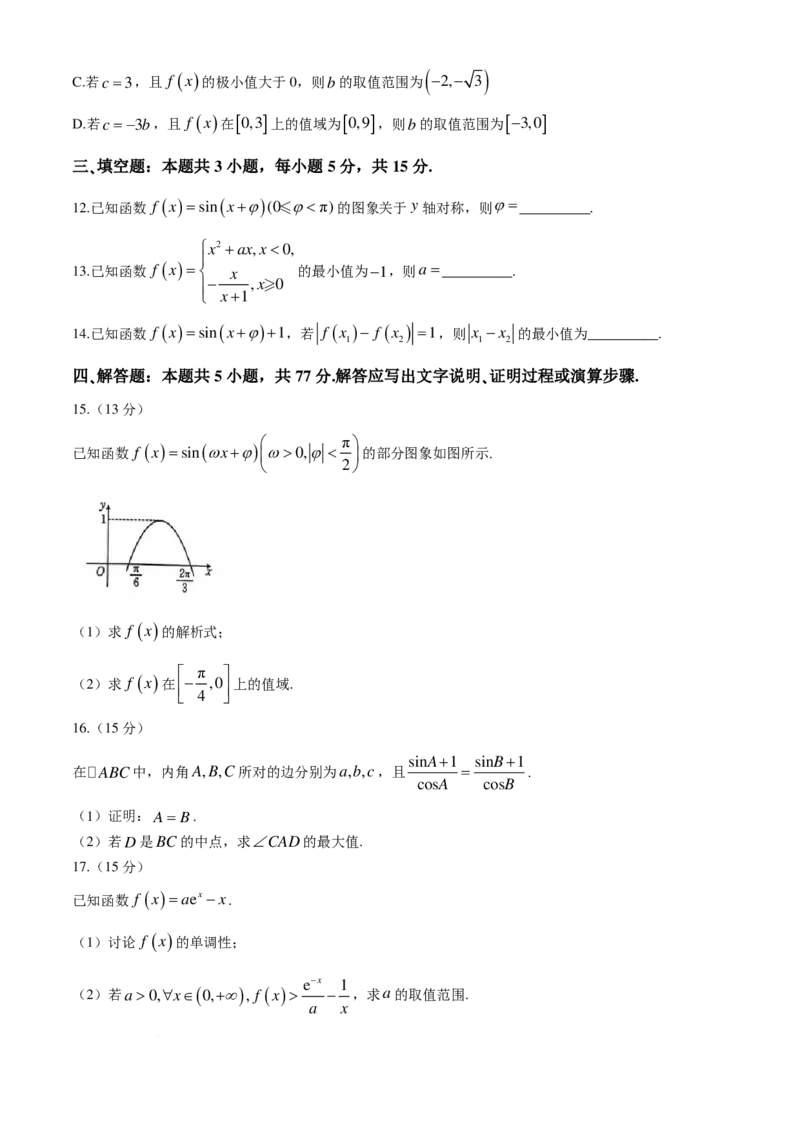15.（13分）  π 已知函数 f ( x )=sin (ωx+ϕ)  ω>0,ϕ< 的部分图象如图所示.  2 ( ) （1）求 f x 的解析式；  π  （2）求 f ( x ) 在  − ,0  上的值域.  4  16.（15分） sinA+1 sinB+1 在ABC中，内角A,B,C所对的边分别为a,b,c，且 = . cosA cosB （1）证明：A= B. （2）若D是BC的中点，求∠CAD的最大值. 17.（15分） 已知函数 f ( x )=aex −x. ( ) （1）讨论 f x 的单调性； e−x 1 （2）若a >0,∀x∈( 0,+∞) , f ( x )> − ，求a的取值范围. a x 学科网（北京）股份有限公司18.（17分） 已知集合A,B中的元素均为正整数，且A,B满足：①对于任意a ,a ∈A，若a ≠ a ，都有aa ∈B； i j i j i j b ②对于任意b ,b ∈B，若b 8 ) ，求t； （3）若A中有4个元素，证明：B中恰有5个元素. 19.（17分） 已知函数 f ( x )= x+( x+a ) lnx. （1）若 f ( x ) 是增函数，求a的取值范围. （2）若 f ( x ) 有极小值，且极小值为m，证明：m1. （3）若 f ( x ) 0，求a的取值范围. 学科网（北京）股份有限公司高三数学试卷参考答案 1.B A∩(  B )= B,B={ 0,2,4 } . U U 5π 5π 5π 3 2.B sin2 −cos2 =−cos = . 12 12 6 2 3.A 令y =0，则 f ( 0 )=0.  1  =4xy, x=2, 1 1  1 1 xy  4.D 2x+ =  +2y2x+  =4+ +4xy4+2 4 =8，当且仅当 即 1 时， y  x  y xy 1 y = +2y =1,  4 x 等号成立. 2x 5.A f′( x )= +cosx，则 f′( 0 )=1，即切线方程为y = x+1. x2 +1 1 令x=0，则y =1，令y =0，则x=−1，故该切线与两坐标轴所围成的三角形的面积为 . 2 θ−θ θ−θ 6.D 因为θ=θ +(θ′−θ) e − 1 4 ，所以t =−4ln θ′−θ 0 .若θ′>θ 0 ，则 f (θ)=−4ln θ′−θ 0 是减函数，因 0 0 0 0 θ−θ 为θ >θ，所以t θ，所以t >t . 1 2 1 2 0 θ′−θ 1 2 1 2 0 7.B 因为log m>1(m,n>0且m≠0,n≠0)，所以m>n>1或0n>1,m−n+1>1,(m−n+1)e >1. 8.C 由题意可得∠BCP=∠ABP=α.在BCP中，BP= BCsinα=6sinα. 在ABP中，AP2 = AB2 +BP2 −2AB⋅BPcosα，即4=36sin2α+16−2× 6sinα⋅4cosα，化简得3cos2α+4sin2α=5，两边平方得9cos22α+16sin22α 9cos22α+16sin22α+24cos2αsin2α +24cos2αsin2α=25，则 =25，所以 cos22α+sin22α 学科网（北京）股份有限公司9+16tan22α+24tan2α 4 =25，解得tan2α= . 1+tan22α 3 0,x0, 9.BC 因为x− x = 所以x− x0，又x2 0，所以x− xx2,p是假命题， 2x,x<0, π  π  π  ¬p是真命题.由诱导公式可得∀α∈  ,π,cos −α  =sin +α ，所以q是真命题， 2  4  4  ¬q是假命题.  1  1 10.AC 因为 f (−x )=cos −x−  =cosx+  = f ( x ) ，所以 f ( x ) 为偶函数，A正确.  x  x ( ) f x 的最大值为1,B错误. 1  5 令函数g ( x )= x+ ,g ( x )在 ( 1,2 ) 上单调递增，且当x∈( 1,2 ) 时，g ( x ) 的值域为2, . x  2  5 因为函数y =cosx在2, 上单调递减，所以 f ( x ) 在 ( 1,2 ) 上单调递减，C正确.  2 当x∈( 1,20 ) 时，g ( x ) 的值域为 ( 2,20.05 ) ,6π<20.05<7π，函数y =cosx在 ( 2,20.05 ) 上有5个零 ( ) ( ) 点，所以 f x 在 1,20 上有5个零点，D错误. 11.BCD 由三次函数的图象可知，若x 是 f ( x ) 的极小值点，则极大值点在x 的左侧， f ( x ) 在 0 0 (−∞,x ) 上不单调，A错误. 0 f′( x )= x2 +2bx+c，若x=b是 f ( x ) 的极大值点，则 f′( b )=b2 +2b2 +c=0，所以 c=−3b2, f′( x )= x2 +2bx−3b2 =( x+3b )( x−b ) .若b=0, f ( x ) 没有极值点. f′( x )=0的解为 x =−3b,x =b.因为x=b是 f ( x ) 的极大值点，所以b<−3b，即b<0,c=−3b2 <0,B正确. 1 2 1 1  若c=3，则 f ( x )= x3+bx2 +3x= x x2 +bx+3, f′( x )= x2 +2bx+3.因为 f ( x ) 的极小值大于 3 3  学科网（北京）股份有限公司1 0，所以 f ( x ) 只有一个零点，且 f ( x ) 的极大值点与极小值点均大于0，所以方程 x2 +bx+3=0无实数 3 根，且方程 f′( x )= x2 +2bx+3=0的2个实数根均大于0， Δ =b2 −4<0, 1  所以Δ =4b2 −12>0解得−20,  1 若c=−3b，则 f ( x )= x3+bx2 −3bx, f′( x )= x2 +2bx−3b, f ( 0 )=0, f ( 3 )=9. 3 令 f′( x )=0，若Δ=4b2 +12b0，即−3b0, f′( x ) 0, f ( x ) 单调递增，符合题意.由 Δ=4b2 +12b>0，解得b<−3或b>0，此时 f′( x )=0的2个解为 x =−b− b2 +3b,x =−b+ b2 +3b .当b>0时，x <0,x >0，所以 f ( x ) 在 ( 0,x ) 上单调递减，即 1 2 1 2 2 当x∈(0，x ) 时， f ( x )<0，不符合题意.当b<−3时，0< x <3，所以 f ( x ) 在 [ 0,3 ] 上的最大值为 2 1 f ( x ) ，且 f ( x )> f ( 3 )=9，不符合题意.综上，若c=−3b，且 f ( x ) 在 [ 0,3 ] 上的值域为 [ 0,9 ] ，则b 1 1 的取值范围为 [−3,0 ] ，D正确. π π π 12. 因为函数 f ( x ) 的图象关于y轴对称，所以ϕ= +kπ,k∈Z.又0 ϕ<π，所以ϕ= . 2 2 2 x 1 13.2 当x0时，y =− = −1>−1.因为 f ( x ) 的最小值为−1，所以函数y = x2 +ax在 x+1 x+1  a − <0,   2 (−∞,0 ) 上取得最小值−1，则 解得a=2.  a2 − =−1,  4 π  π  π  14. 3 根据三角函数的周期性和对称性，不妨设x 1 +ϕ∈   0, 2   ,x 2 +ϕ∈   − 2 ,0   .因为 x +x +2ϕ x −x f ( x )− f ( x ) =1，所以sin ( x +ϕ)−sin ( x +ϕ)=1=2cos 1 2 ⋅sin 1 2 ，即 1 2 1 2 2 2 x −x 1 1 sin 1 2 =  x −x π π 2 x +x +2ϕ 2，所以 1 2  ，即x −x  ，当且仅当 2cos 1 2 2 6 1 2 3 2 学科网（北京）股份有限公司π π x +ϕ= ,x +ϕ=− 时，等号成立. 1 6 2 6 T 2π π π 2π 15.解：（1）由图可得， = − = ，所以T =π= . ω 2 3 6 2 结合ω>0，解得ω=2，则 f ( x )=sin ( 2x+ϕ) . π  π  π π 由 f   =sin2× +ϕ  =0，结合图象可得 +ϕ=2kπ,k∈Z，即ϕ=− +2kπ,k∈Z. 6  6  3 3 π π 因为ϕ< ，所以ϕ=− ， 2 3  π 所以 f ( x )=sin2x− .  3  π  π  5π π （2）因为x∈  − ,0  ，所以2x− ∈  − ,−  ，  4  3  6 3  π   1 所以 f ( x ) 在  − ,0  上的值域为  −1,− .  4   2 2 2  A A  B B sinA+1 sinB+1 sin +cos  sin +cos  16.（1）证明：因为 = ，所以  2 2  =  2 2  , cosA cosB A A B B cos2 −sin2 cos2 −sin2 2 2 2 2 A A B B sin +cos sin +cos 2 2 2 2 则 = . A A B B cos −sin cos −sin 2 2 2 2 A B A B  A B 则sin cos −cos sin =0，即sin −  =0. 2 2 2 2  2 2  A B 因为A,B∈( 0,π ) ，所以 − =0，即A= B. 2 2 AC2 AC2 + AD2 − （2）解： AC2 + AD2 −CD2 4 cos∠CAD= = 2AC⋅AD 2AC⋅AD 3AC2 + AD2 4 3AC AD 3AC AD 3 ， = = + 2 ⋅ = 2AC⋅AD 8AD 2AC 8AD 2AC 2 学科网（北京）股份有限公司π AD 3 所以∠CAD ，当且仅当 = 时，等号成立. 6 AC 2 π 故∠CAD的最大值为 . 6 17.解：（1） f′( x )=aex −1. 当a0时， f′( x )<0, f ( x ) 是减函数. 当a>0时，y = f′( x ) 是增函数.令 f′( x )=0，解得x=−lna. 当x∈(−∞,−lna ) 时， f′( x )<0；当x∈(−lna,+∞) , f′( x )>0. 所以 f ( x ) 在 (−∞,−lna ) 上单调递减，在 (−lna,+∞) 上单调递增. 综上，当a0时， f ( x ) 是减函数；当a>0时， f ( x ) 在 (−∞,−lna ) 上单调递减，在 (−lna,+∞) 上单调 递增. e−x 1 e−x 1 （2） f ( x )> − ，即aex − > x− . a x a x 令函数g ( x )= x− 1 ，则g ( aex ) =aex − e−x ，所以g ( aex) > g ( x ) . x a x 因为g ( x ) 在 ( 0,+∞) 上单调递增，所以aex > x，即a > . ex x 1−x 令函数h ( x )= ( x>0 )，则h′( x )= . ex ex 当x∈( 0,1 ) 时，h′( x )>0；当x∈( 1,+∞) ,h′( x )<0. 所以h ( x ) 在 ( 0,1 ) 上单调递增，在 ( 1,+∞) 上单调递减， 1 1 所以h(x) =h ( 1 )= ,a>h(x) = . 极大值 极大值 e e 1  故a的取值范围为 ,+∞ . e  18.（1）解：由①可得2,4,8都是B中的元素. 下面证明B中除2,4,8外没有其他元素： 假设B中还有其他元素，分两种情况： 学科网（北京）股份有限公司8 第一种情况，B中最小的元素为1，显然 不是A中的元素，不符合题意； 1 第二种情况，B中最小的元素为2，设B中除2,4,8外的元素为b ( b >2 ) ， k k b 因为 k 是A中的元素，所以b 为4或8，而4，8也是B中的元素， k 2 所以B中除2,4,8外没有其他元素. 综上，B={ 2,4,8 } . （2）解：由①可得，8,16,32,2t,4t,8t都是B中的元素. 4t 2t 2t t t t 显然8<4t,8<2t,16<2t，由（2）可得， , , 是A中的元素，即 , , 是A中的元素. 8 8 16 2 4 8 t t t t t t 因为 < < a ，所以 3 1 不可能是A中的元素，不符合题意. 1 aa a 4 aa 1 2 2 1 2 a a a a 若a 1 2，则 a 2 < a 3 a4，与A= { a ,a2,a3,a4} 矛盾. 1 k k 1 1 1 1 1 学科网（北京）股份有限公司k k 若k >a3，因为 ∈A，所以 =ai,i =1,2,3,4，则k =ai+3,i =1,2,3,4， 1 a3 a3 1 1 1 1 即k∈ { a4,a5,a6,a7} ，所以B中除a3,a4,a5,a6,a7外，没有其他元素. 1 1 1 1 1 1 1 1 1 所以B= { a3,a4,a5,a6,a7} ，即B中恰有5个元素. 1 1 1 1 1 a 19.（1）解： f′( x )=lnx+ +2. x a x−a 令函数g ( x )=lnx+ +2，则g′( x )= . x x2 若a>0，则当x∈( 0,a ) 时，g′( x )<0，当x∈( a,+∞) 时，g′( x )>0，所以g ( x ) 在 ( 0,a ) 上单调递 减，在 ( a,+∞) 上单调递增，g(x) = g ( a )=lna+3. min 1 因为 f ( x ) 是增函数，所以 f′(x) 0，即g(x) 0，解得a . min min e3 若a0，则g′( x )>0在 ( 0,+∞) 上恒成立，所以g ( x ) 在 ( 0,+∞) 上单调递增. a a 因为函数y =lnx+2与函数y =− 的图象有1个交点，所以存在x ，使得lnx + +2=0，即当 x 0 0 x 0 x∈( 0,x ) 时，g ( x )<0，当x∈( x ,+∞) 时，g ( x )>0，所以 f ( x ) 在 ( 0,x ) 上单调递减，在 0 0 0 ( x ,+∞) 上单调递增，与题设不符. 0  1  综上，a的取值范围为  ,+∞ . e3  1 ( ) （2）证明：由（1）可得当a 时， f x 是增函数，不存在极小值. e3 1 当00，所以∃x ∈( a,1 ) ,g ( x )=0， 1 1 所以 f ( x ) 在 ( a,x ) 上单调递减，在 ( x ,+∞) 上单调递增. 1 1 f(x) = f ( x )< f ( a )=a+( a+a ) lna0，  e3  e3   1   1  所以h ( x ) 在0, , ( 1,+∞) 上单调递减，在 ,1上单调递增.  e3  e3   1   1 2 5 当x∈ 0, 时，lnx<−3,(lnx)2 +lnx−1= lnx+  − >0，  e3   2 4 所以h ( x )=−x  (lnx)2 +lnx−1  <0. 因为h(x) =h ( 1 )=1，所以h ( x ) 1， 极大值 所以 f(x) 1，当且仅当x =1,a =−2时，等号成立. 极小值 0 综上，m1.  1  1  1  2 （3）解：若a>0, f   = −3 +a =− −3a<0，不符合题意. e3  e3 e3  e3 若a0，要使得 f ( x ) 0，只需要 f(x) 极小值 0，即−x 0   ( lnx 0 )2 +lnx 0 −1  0， 所以( lnx 0 )2 +lnx 0 −10，解得 −1− 2 5 lnx 0  −1+ 2 5 ，即 e −1− 2 5 x 0 e −1+ 2 5 . a =−x lnx −2x ，令函数u ( x )=−xlnx−2x，则u′( x )=−lnx−3. 0 0 0  1  当x∈  ,+∞ 时，u′( x )<0,u ( x ) 单调递减. e3  −1− 5 1 ( )  −1− 5 −1+ 5 因为e 2 > ，所以u x 在e 2 ,e 2 上单调递减. e3    −1− 5  −3+ 5 −1− 5  −1+ 5  3+ 5 −1+ 5 又ue 2 = e 2 ,ue 2 =− e 2 ，     2 2      −1− 5 −1+ 5  3+ 5 −1+ 5 −3+ 5 −1− 5 所以u ( x ) 在e 2 ,e 2 上的值域为− e 2 , e 2 .    2 2  学科网（北京）股份有限公司 3+ 5 −1+ 5 −3+ 5 −1− 5 故a的取值范围为− e 2 , e 2 .  2 2  学科网（北京）股份有限公司