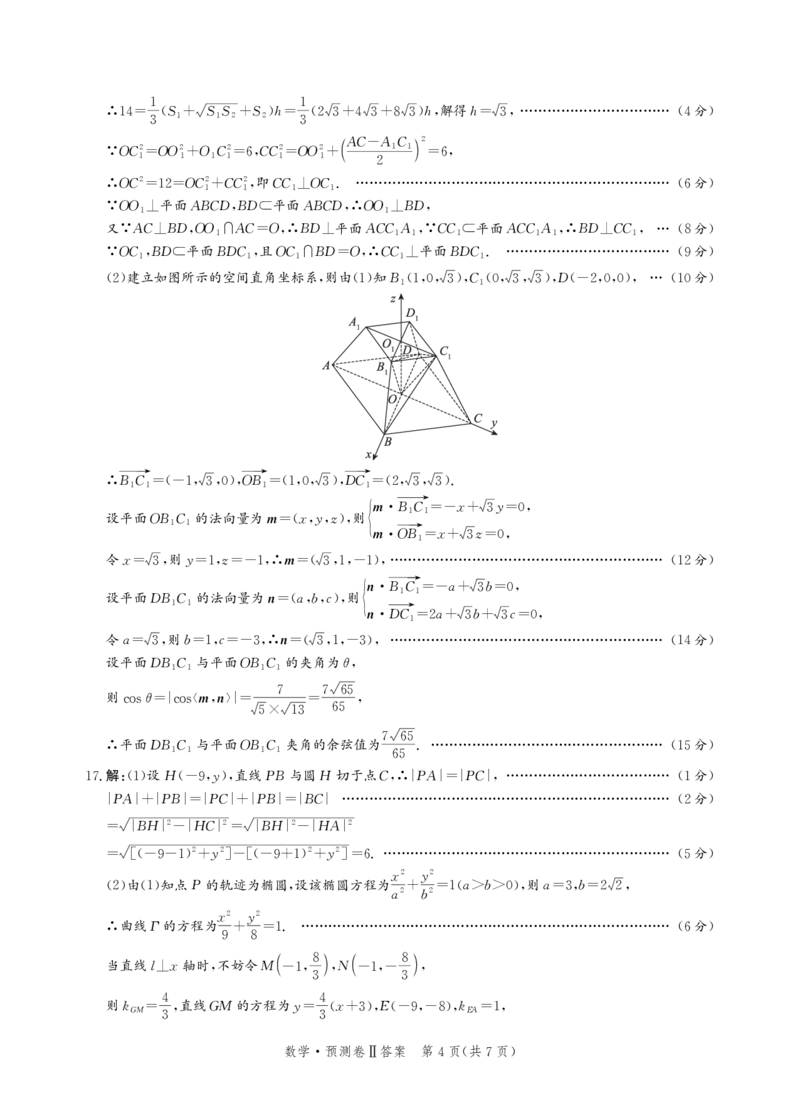文档内容
高三省级联测考试
2024-2025
数学参考答案
本套试卷的命制以拓展思维为主,参照近几年高考数学试卷的新题型进行模拟,以
拒绝模式化试题和套路形试题为命题思路,力争在数学思维延伸、数学思想创新、数学
基本方法拓展和数学技巧应用上均有所突破。 本套试卷全面考查学生的数学素养,以选
拔人才为出发点,兼顾考查学生的数学品质为准则,试题从易到难,层层递进,综合考查
了高中阶段的主干知识。
一、立足数学核心素养
该套试题涵盖了数学的六大核心素养——数学抽象、逻辑推理、数学建模、直观想
象、数学运算和数据分析,引导学生从刷题思维向运用思维、发散思维、拓展思维、创新
思维转化。
二、考查基本方法和基本知识点
本套试题符合高考试题的与时俱进性和创新性。 考查的内容不追求符合全体学生预
期但追求选拔性考查的思路,兼顾试题的基本知识和基本方法的合理性综合延伸。 例
如,第 题利用三角函数的切化弦,延伸到两角和差公式;第 题利用两点的距离延伸到
5 8
焦半径,再与点差法结合求出点P坐标;第 题利用抽象函数与基本初等函数的关系进
13
行创新,考查了学生的数学直觉,是考查学生应变能力非常好的试题。 整套试题包含数
形结合、构造函数等数学思想、方法的考查。
三、命制试题亮点
本套试题中的第 , 题是整套试题的亮点题目,其中,第 题是圆锥曲线的创新试题,
8 19 8
将基本知识和方法从全新的角度去命制;第 题是源于课本又高于课本的不定方程试题,它
19
是和整除、均值方差、排列组合、概率综合在一起的非常新颖的试题,难度大,背景新。
题号
1 2 3 4 5 6 7 8 9 10 11
答案
A B B C A D B C AB ABD ABD
. 解析: M N N N M M 则 a a 此时a N M成立 故选 .
1A ∵ ∩ = ,∴ ⊆ ,-2∈ , -2= -1,=-1, +1=0, ⊆ , A
. 解析:由a b可得 a b 又由 b b 可得 a b 又由 a b 不一定可得a b 反例
2B > 2>2, 2>2-1, 2>2-1, 2>2-1 > , :
当a 1b 时 a b 成立 但a b a b 是a b的必要不充分条件 故选 .
= ,=1 ,2>2-1 , < ,∴“2>2-1” “> ” , B
2
m nm
. 解析:向量n在向量m上的投影向量p · 2 4 故选 .
3B = m m = ,- , B
| || | 5 5
. 解析:设等差数列a 的公差为d a a a a a 又由根与系数的关系得a a
4C {n} ,∵ 1+ 3= 6,∴22= 6, 3+ 5=12=
a a a a d a a n d n a S 1na a 1nn 故选 .
2+ 6,∴ 2=4,6=8,∴ =1,n = 2+(-2)= +2,1=3,n = (1+ n)= (+5), C
2 2
数学·预测卷 答案 第 页(共 页)
Ⅱ 1 7
{#{QQABRQA4wgiQgFbACZ5KAw0GCwmQsJAgLWoMBVCRKAwLQYNABIA=}#}5
.
A
解析:由已知得 1
β =
1
α -
1
α ,
即cos
β
β
=
1-co
α
s
α
,∴cos
β
sin
α
=sin
β
-sin
β
cos
α
,
即
sin(
α
+
tan sin tan sin sin
β β αβ π α β β 即 β α 故选 .
)=sin ,∵ ,∈0, ,∴ + =π- , 2+ =π, A
2
. 解析:设hx x x gx xx 当x 时 x gx
6D ()=1+log a(+1)(>1),()=4-2(≤1), ≤1 ,0<2≤2,()∈[2,4),
fx 的值域为 a hx a 3 故选 .
∵ () [2,+∞),∴ >1,()∈(1+log a 2,+∞),∴2≤1+log a 2<4,∈(2,2], D
h
. 解析:设圆锥的高为h 底面半径为rr 则圆锥内接的圆柱上面的小圆锥的高为h -2
7B , (>1), -2,∴ =
1
h r r3 r2 r
h 2 该圆锥的体积V 1r2h 2π 则V' 2π (2 -3)令V' 则r 3 当 r
r,∴ =r -1 , = 3 π = 3( r -1) , = 3( r -1) 2 , =0, = 2 , 1< <
3时V' 当r 3时V' r 3时V取得最小值为9 故选 .
, <0, > , >0,∴ = , π, B
2 2 2 2
c
. 解析:设Fc Ax y Bx y 弦AB的中点为Mx y 离心率为e 则 AF
8C (,0), (1,1), (2,2), (0,0), =a, | |=
b2 x2 y2 x2
x c2 y2 x2 cx c2 x2 b2 ex a 同理 BF ex a .由 1 1 2
(1- )+ 1= 1-2 1+ +a2 1- =| 1- |, | |=| 2- | a2-b2=1,a2-
y2 y y b2x x b2x
2 两式相减整理得k 1- 2 (1+ 2) 0 弦AB的垂直平分线方程为y y
b2=1 AB =x x =a2y y =a2y,∴ - 0=
1- 2 (1+ 2) 0
a2y
0x x 令y 得x e2x 则Pe2x .AB AF BF ex a ex a ex
-b2x (- 0), =0, = 0, ( 0,0)| |=| |+| |= 1- + 2- =2( 0
0
a 此时P在F的右侧 PF e2x c eex a 由AB PF 得 ex a eex a
- ), ,| |= 0- = ( 0- ),| |=| |, 2( 0- )= ( 0- ),∵
x c ex a e 故选 .
0> ,∴ 0- >0,∴ =2, C
. 解析:z 2 3 其虚部是 正确z 2 3 4 z
9AB 3=i+2i+3i=-2-2i, -2,∴A ;4=i+2i+3i+4i=2-2i,∴|3|=
z
| z 4|,∴B 正确 ; z 6=i+2i 2 +3i 3 +4i 4 +5i 5 +6i 6 =-4+3i, z 6 z 6=| z 6| 2 =25,∴C 不正确 ; z 6 = -4+3i =
-2-i
2
不正确 故选
1-2i,∴D , AB.
. 解析:f'x x a
b
2
x2
+
ax
+
b
f'x x2 x 恒成立 f'x 与x2
10ABD ()=2 + +x= x ,∵ ()( -3 +2)≥0 ,∴ ()=0 -
a b
x 有相同的根 即 x2 ax b 的两个实数根为 即a b .
3 +2=0 , 2 + + =0 1,2,∴- =3, =2, =-6,=4
2 2
a a
fx x2 x x 由f'x 得 x 或x b 5 b
∴ ()= -6 +4ln , ()>0 0< <1 >2,∵ +b= ,∴ +b,+∞ ⊆(2,+∞),
2
正确 当x 时f'x 函数fx 单调递增 当x 时f'x 函数fx 单调递
∴A ; ∈(0,1) , ()>0, () , ∈(1,2) , ()<0, ()
减 当x 时f'x 函数fx 单调递增 fx 在x 处取得极大值f 在
, ∈(2,+∞) , ()>0, () ,∴ () =1 (1)=-5<0,
x 处取得极小值f 又当x 时fx 正确 不正确 正确
=2 (2)=-8+4ln2<0, →+∞ ,()→+∞,∴B ,C ,D ,
故选
ABD.
. 解析:甲获胜的概率为2 2 1 2 1 2 2 1 2 1 1 2 1 2 188
11ABD × +C2× × × +C2× × ×C2× × × = ,∴
3 3 3 3 3 3 3 3 3 3 243
正确 两人比赛 局结束的概率为 1 2 1 2 2 1 2 1 1 2 20 正确 对于
A ; 4 C2× × × +C2× × × = ,∴B ; C,
3 3 3 3 3 3 81
比赛进入第三局 前两局是 平 则在第三局甲赢的条件下乙赢得胜利的概率为
∵ ,∴ 1∶1 ,
数学·预测卷 答案 第 页(共 页)
Ⅱ 2 7
{#{QQABRQA4wgiQgFbACZ5KAw0GCwmQsJAgLWoMBVCRKAwLQYNABIA=}#}2
1 2 1 2 1
C2× × × ×
3 3 3 3 1 不正确 由 知 乙获胜的概率为 188 55 在此条件下 乙赢得
= ,∴C ; A , 1- = , ,
1 2 1 2 9 243 243
C2× × ×
3 3 3
2 2
1 2 1 1 2 1 1 2 1 1
+ × × + × ×C2× × ×
第二局胜利的概率为 3 3 3 3 3 3 3 3 3 41 正确 故选
= ,∴D , ABD.
55 55
243
. π
12 0,
3
数学·预测卷 答案 第 页(共 页)
Ⅱ 3 7
解析:当直线l过圆心C时 两条切线平行 所以夹角为 当直线l不过
, , 0,
圆心C时 如图 设两条切线交于点D 则 D ACB 设点C到直线l的距
, , , ∠ =π-∠ ,
离为d 则d 当d 时 斜率不存在 则 D ACB
, ∈(0,1)( =1 , ), cos∠ =cos(π-∠ )=
ACB d 2 d2
ACB 2 ∠ 1
-cos∠ =1-2cos =1-2· =1- ∈ ,1 ,
2 2 2 2
D π 综上 两条切线夹角的取值范围是 π
∴∠ ∈0, , , 0,
3 3
.
.fx x 答案不唯一 解析:fx y 中间符号为 fxfy f π xf π y 前后
13 ()=cos2 ( ) (- ) “-”,()()+ - -
4 4
两个代数式中间符号为 所以类比两角差的余弦公式 α β α β α β 但
“+”, cos(- )=cos cos +sin sin ,
π α α 故fx 的一个解析式为fx x 按诱导公式与周期性 也可取fx
cos - =sin , () ()=cos2 , , ( )=
2
xfx xfx x .
cos10 ,()=cos18 ,()=cos26 ,…
. 解析:由抛物线的性质知y y y y MN y y y y .直线
143 A =2 M,B =2 N,| |=23=| M - N |,∴| A - B |=43
p
AB的方程为y x 代入抛物线方程整理得 y2 py p2 解得y py
= 3 - , 3 -2 - 3 =0, 1= 3 ,2=
2
3p 不妨设点A在第一象限 则y py 3p y y 43p p .
- , , A =3 ,B =- ,∴| A - B |=43= ,∴ =3
3 3 3
.解:()由余弦定理得 b2 c2 bc,
15 1 49= + -
联立 c b ,解得c (舍)或c ,…………………………………………………………… (分)
2- =2 =-3 =5 4
a c
由正弦定理得 ,
A= C
sin sin
解得 C 53.……………………………………………………………………………………… (分)
sin = 6
14
()由题得 ABC的面积S 1ah 1 123 , 1bc A 3bc ,
ABC
2 △ △ = = ×7× =63 ∴ sin = =63
2 2 7 2 4
bc . ……………………………………………………………………………………………… (分)
∴ =24 9
由余弦定理得 b2 c2 bc,
49= + -
b2 c2 ,………………………………………………………………………………………… ( 分)
∴ + =73 11
(b c) 2 ,b c ,
∴ + =73+48=121∴ + =11
ABC的周长为a b c .…………………………………………………………………… ( 分)
∴△ + + =18 13
.解:()由已知得AC ,AC .
16 1 =43 1 1=23
设OO h,上底面ABCD 的面积S 3 2 ,下底面ABCD的面积S 3 2
1= 1 1 1 1 1=2× ×2=23 2=2× ×4=
4 4
,……………………………………………………………………………………………………… (分)
83 2
{#{QQABRQA4wgiQgFbACZ5KAw0GCwmQsJAgLWoMBVCRKAwLQYNABIA=}#}1(S SS S)h 1( )h,解得h ,…………………………… (分)
∴14= 1+ 1 2+ 2 = 23+43+83 =3 4
3 3
OC2 OO2 OC2 ,CC2 OO2 AC - A 1 C 1 2 ,
∵ 1= 1+ 1 1=6 1= 1+ =6
2
OC2 OC2 CC2 ,即CC OC. …………………………………………………………… (分)
∴ =12= 1+ 1 1⊥ 1 6
OO 平面ABCD,BD 平面ABCD,OO BD,
∵ 1⊥ ⊂ ∴ 1⊥
又 AC BD,OO AC O,BD 平面ACCA ,CC 平面ACCA ,BD CC, … (分)
∵ ⊥ 1∩ = ∴ ⊥ 1 1 ∵ 1⊂ 1 1 ∴ ⊥ 1 8
OC,BD 平面BDC,且OC BD O,CC 平面BDC. ……………………………… (分)
∵ 1 ⊂ 1 1∩ = ∴ 1⊥ 1 9
()建立如图所示的空间直角坐标系,则由()知B (,, ),C(, , ),D( ,,), … ( 分)
2 1 110 3 10 3 3 -200 10
BC→ ( , ,),OB→ (,, ),DC→ (, , ).
∴ 1 1= -1 30 1=10 3 1=2 3 3
m·BC→ x y ,
设平面OBC 的法向量为m (x,y,z),则 1 1=- +3 =0
1 1 = m·OB→ x z ,
1= +3 =0
令x ,则 y ,z ,m ( ,, ),…………………………………………………… ( 分)
=3 =1 =-1∴ = 31-1 12
n·BC→ a b ,
设平面DBC 的法向量为n (a,b,c),则 1 1=- +3 =0
1 1 = n·DC→ a b c ,
1=2 +3 +3 =0
令a ,则b ,c ,n ( ,, ),…………………………………………………… ( 分)
=3 =1 =-3∴ = 31-3 14
设平面DBC 与平面OBC 的夹角为θ,
1 1 1 1
则 θ 7 7 65,
cos =|cos |= =
5× 13 65
平面DBC 与平面OBC 夹角的余弦值为7 65.…………………………………………… ( 分)
∴ 1 1 1 1 15
65
.解:()设H( ,y),直线PB与圆H切于点C, PA PC ,……………………………… (分)
17 1 -9 ∴| |=| | 1
PA PB PC PB BC ……………………………………………………………… (分)
| |+| |=| |+| |=| | 2
BH 2 HC2 BH 2 HA2
= | |-| | = | |-| |
[( ) 2 y2 ] [( ) 2 y2 ] .……………………………………………………… (分)
= -9-1 + - -9+1 + =6 5
()由()知点P的轨迹为椭圆,设该椭圆方程为
x2 y2
(a b ),则a ,b ,
2 1 a2+b2=1 > >0 =3 =22
曲线Γ的方程为
x2 y2
. ……………………………………………………………………… (分)
∴ + =1 6
9 8
当直线l x轴时,不妨令M ,8 ,N , 8 ,
⊥ -1 -1-
3 3
则k 4,直线GM的方程为 y 4(x ),E( , ),k ,
GM EA
= = +3 -9-8 =1
3 3
数学·预测卷 答案 第 页(共 页)
Ⅱ 4 7
{#{QQABRQA4wgiQgFbACZ5KAw0GCwmQsJAgLWoMBVCRKAwLQYNABIA=}#}同理k ,EA FA, 点A在以EF为直径的圆上;……………………………………… (分)
FA
=-1∴ ⊥ ∴ 8
当直线l不垂直于x轴时,设M(x,y),N(x,y),直线l的方程为 y k(x ),…………… (分)
1 1 2 2 = +1 9
代入Γ:x2 y2 中,整理得( k2 )x2 k2x k2 ,
8 +9 =72 8+9 +18 +9 -72=0
x x 18
k2
,xx 9
k2
-72. …………………………………………………………… ( 分)
∴ 1+ 2=- k2 1 2= k2 11
8+9 8+9
y k(x )
直线MG的方程为 y 1 (x ),即 y 1+1 (x ),………………………………… ( 分)
=x +3 = x +3 12
1+3 1+3
k(x ) k(x )
E , 6 1+1 ,同理F , 6 2+1 ,
∴ -9- x -9- x
1+3 2+3
k2 (x )(x ) k2 (xx x x )
A( ,),EA→·FA→ 36 1+1 2+1 36 1 2+ 1+ 2+1 ,EA FA,
∵ -10 ∴ =64+ (x )(x ) =64+ xx (x x) =0∴ ⊥
1+3 2+3 1 2+3 1+ 2 +9
………………………………………………………………………………………………………… ( 分)
14
点A在以EF为直径的圆上.……………………………………………………………………… ( 分)
∴ 15
x
.解:()当a 时,f(x) (x ) 2 ,x ( , ),
18 1 =2 =ln +1-x ∈ -1+∞
+2
f'(x) 1 4
x2
恒成立,…………………………………………… (分)
=x -(x ) 2=(x )(x ) 2≥0 2
+1 +2 +1 +2
f(x)在( , )上单调递增,又 f() ,
∴ -1+∞ 0=0
f(x) 的解集为[, ).……………………………………………………………………… (分)
∴ ≥0 0+∞ 5
()f'(x) 1 2
a x2
+
(
4-2
a)x
+4-2
a
,…………………………………………… (分)
2 =x -(x ) 2= (x )(x ) 2 6
+1 +2 +1 +2
由 f'(x) 得x2 ( a)x a ,
=0 +4-2 +4-2 =0
若Δ ,解得 a ,此时 f'(x) 恒成立,
≤0 0≤ ≤2 ≥0
f(x)在(, )上单调递增,f(x)f() ; ……………………………………………… (分)
∴ 0+∞ ∴ ≥ 0=0 7
若Δ ,解得a 或a ,
>0 <0 >2
x , 当a 时,f'(x) ,f(x)在(, )上单调递增,f(x)f() ;…………… (分)
∵ ≥0∴ <0 ≥0 0+∞ ∴ ≥ 0=0 8
当a 时,由 f'(x) 解得 x a a2 a,
>2 <0 0≤ < -2+ -2
f(x)在(,a a2 a)上单调递减,f(x)f() ,f(x) 不恒成立.…………… (分)
∴ 0 -2+ -2 ∴ < 0=0 ≥0 9
当x 时,f(x) 恒成立,实数a的取值范围是( ,].………………………………… ( 分)
∴ ≥0 ≥0 -∞2 10
x
()取a ,由()知,当x 时,f(x) (x ) 2 ,………………………………… ( 分)
3 =2 1 ≥0 =ln +1-x ≥0 11
+2
(x )x 2
x
x,即 (x )
x2
x.……………………………………………… ( 分)
∴ln +1+ -x ≥ ln +1+x ≥ 12
+2 +2
(n ) x
故只需证明x
≥ n
+1si n
x
, ……………………………………………………………………… (
13
分)
+cos
(n ) x
设 g(x)
=
x
- n
+1si n
x
,
+cos
g'(x)
(n
+1
)
cos
x(n
+cos
x)
+
(n
+1
)
sin
2x
∴ =1- (n x) 2
+cos
(
cos
x
-1
)[
cos
x
-
(n2
-
n
-1
)]
, ……………………………………………………………… ( 分)
= (n x) 2 14
+cos
n ,n2 n ,g'(x) ,g(x)在[, )上单调递增,………………………… ( 分)
∵ ≥2∴ - -1≥1∴ ≥0∴ 0+∞ 15
(n ) x
∴
g(x)
≥
g(
0
)
=0
,
∴
x
≥ n
+1si n
x
成立,……………………………………………………… (
16
分)
+cos
数学·预测卷 答案 第 页(共 页)
Ⅱ 5 7
{#{QQABRQA4wgiQgFbACZ5KAw0GCwmQsJAgLWoMBVCRKAwLQYNABIA=}#}即
ln
(x
+1
)
+x
x2
≥
(n
n
+1
)
si n
x
x
成立.…………………………………………………………… (
17
分)
+2 +cos
.解:() .,
19 1 ∵2025÷6=3375
(x,x,…,x)是 极值时,x,x,…,x 中有三个 和三个 , ……………………… (分)
∴ 1 2 6 1·- 1 2 6 337 338 3
∙∙∙
即有
3
组 极值的解.………………………………………………………………………… (分)
C6=20 1·- 4
∙∙∙
()x 1(x x x x x x) .,…………………………………………………… (分)
2 = 1+ 2+ 3+ 4+ 5+ 6 =3375 5
6
x i (i ,,…,)的方差σ2 1[(x x ) 2 (x x ) 2 … (x x ) 2 ] 1(6x i2 x 2 ) 1(S
=12 6 = 1- + 2- + + 6- = i∑ -6 = -
6 6 =1 6
x 2 ),…………………………………………………………………………………………………… (分)
6 6
S σ2 x 2 ,x 为常数, 当方差σ2 最小时S最小.………………………………………… (分)
∴ =6 +6 ∵ ∴ 7
当k 时,x x … x 不是整数舍去,………………………………………………………… (分)
=0 1= 2= = 6 8
当k 时,即(x,x,…,x)是方程E的 极值的一组解时,方差σ2 最小,即S最小,
=1 1 2 6 1·-
∙∙∙
此时S最小 ( 2 2 ) . …………………………………………………………… (分)
=3×337+338 =683439 9
()考虑(x,x,…,x)是方程E的 极值的一组解时的一种情况( , , , , , ),由
3 1 2 6 1·- 337337337338338338
∙∙∙
()知有 组,
1 20
若化为 极值,只需将个位中的一个 减去 ,加到另一个 上,或是将个位中的一个 减去 ,加到另
2·- 7 1 7 8 1
∙∙∙
一个 上,……………………………………………………………………………………………… ( 分)
8 10
即个位化为 ,,,,,或是 ,,,,,,
678888 777789
则方程E的 极值的个数为
4 2 4 2
.………………………………………………… ( 分)
2·- C6A2+C6A2=60 12
∙∙∙
极值是 极值中的n(n ,,)个个位 减去 ,加到n个 上;或是一个 减去 ,另两个 各加
3·- 1·- =123 7 1 8 7 2 7
∙∙∙ ∙∙∙
;或是两个 各减 加到另一个 上,其个位形式为 ,,,,,或是 ,,,,, 或是 ,,,,,
1 8 1 8 677889 667899 666999
或是 ,,,,,或是 ,,,,,.……………………………………………………………… ( 分)
588888 777770 14
其个数为 , …………………………………………………… ( 分)
2 2 2 2 2 2 3
C6C4A2+C6C4A2+C6+6+6=392 16
在k 的前提下,k 时方程E的k 极值的概率 60 15.………………… ( 分)
∴ ≤3 =2 ·- = = 17
∙∙∙ 20+60+392 118
数学·预测卷 答案 第 页(共 页)
Ⅱ 6 7
{#{QQABRQA4wgiQgFbACZ5KAw0GCwmQsJAgLWoMBVCRKAwLQYNABIA=}#}编写细目表
.能力要求
1 :
. 抽象概括能力 . 推理论证能力 . 运算求解能力
Ⅰ Ⅱ Ⅲ
. 空间想象能力 . 数据处理能力 . 应用意识和创新意识
Ⅳ Ⅴ Ⅵ
.核心素养
2 :
数学抽象 逻辑推理 数学建模 直观想象 数学运算 数据分析
① ② ③ ④ ⑤ ⑥
能力要求 核心素养
题号 题型 分值 知识点 难度
Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ ① ② ③ ④ ⑤ ⑥
选择题 分 集合的运算 易
1 5 √ √
选择题 分 不等式与充要条件 易
2 5 √ √ √ √
选择题 分 向量的坐标运算与投影向量 易
3 5 √ √ √ √
选择题 分 等差数列的性质 易
4 5 √ √ √ √ √
选择题 分 两角和的正弦公式 中
5 5 √ √ √ √
选择题 分 分段函数的性质 中
6 5 √ √ √ √ √
选择题 分 几何体体积与导数 中
7 5 √ √ √ √ √ √ √
选择题 分 双曲线的性质与点差法 难
8 5 √ √ √ √ √ √ √ √ √
选择题 分 复数性质与运算 易
9 6 √ √ √ √ √ √
选择题 分 函数与导数 中
10 6 √ √ √ √ √ √ √
选择题 分 概率与条件概率 难
11 6 √ √ √ √ √ √ √ √
填空题 分 直线与圆 易
12 5 √ √ √ √ √ √ √
填空题 分 抽象函数与三角函数 中
13 5 √ √ √ √ √ √
填空题 分 抛物线及其性质 中
14 5 √ √ √ √ √ √ √
解答题 分 解三角形 易
15 13 √ √ √ √ √ √
解答题 分 空间向量与立体几何 易
16 15 √ √ √ √ √ √
解答题 分 直线与椭圆的位置关系 圆 中
17 15 、 √ √ √ √ √ √ √ √ √
解答题 分 导数与不等式 中
18 17 √ √ √ √ √ √
新定义 均值方差 排列组合
解答题 分 、 、 、 难
19 17 概率 √ √ √ √ √ √ √ √ √
数学·预测卷 答案 第 页(共 页)
Ⅱ 7 7
{#{QQABRQA4wgiQgFbACZ5KAw0GCwmQsJAgLWoMBVCRKAwLQYNABIA=}#}