文档内容
2024-2025 学年吉林省普通高中 G8 教考联盟高二(下)期末考试
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合 , ,则 ( )
2
A. ={2,3,4,6} B . ={ | −10> 0}C. ∩ = D.
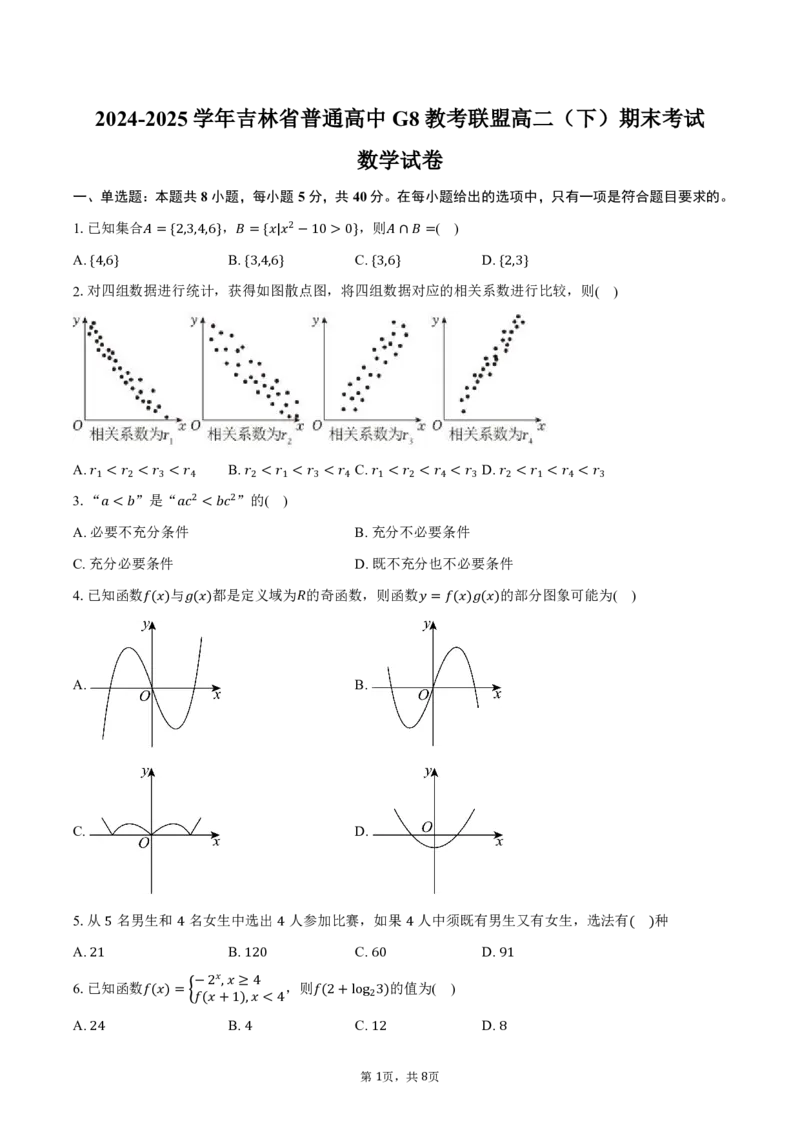
2.对{4四,6}组数据进行统计,获得{3如,4,图6}散点图,将四组{3数,6}据对应的相关系数{2进,3}行比较,则( )
A. B. C. D.
3.“ 1 < 2”<是 3“< 4 ” 的2 <( 1 ) < 3 < 4 1 < 2 < 4 < 3 2 < 1 < 4 < 3
2 2
A.必 要<不 充分条件 < B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
4.已知函数 与 都是定义域为 的奇函数,则函数 的部分图象可能为( )
( ) ( ) = ( ) ( )
A. B.
C. D.
5.从 名男生和 名女生中选出 人参加比赛,如果 人中须既有男生又有女生,选法有 种
A. 5 4 B. 4 C. 4 D. ( )
21 120 60 91
6.已知函数 ,则 的值为( )
−2 , ≥ 4
( )= (2+log23)
A. ( +B1.), <4 C. D.
24 4 12 8
第 页,共 页
1 87.已知正实数 , 满足 ,则 的最小值为( )
2 + =2 +
A. B. C. D.
3 3
2+ 2 2+2 2 2+ 2 2+2 2
8.已知函数 若关于 的方程 有 个不相等的实数根,则
|2 −1|, <2, 2
( )= [ ( )] − ( )− −1=0 4
实数 的取值范围是( −)3, ≥2,
A. B. C. D.
二、−1多<选 题<:0本题共3小题,0共< 18<分1。在每小题−给1出<的 选<项1中,有多0项≤符 合<题1目要求。
9.下列叙述正确的是( )
A.不等式 的解集是
1 1
B.函数 <2 与 { | 是 > 同2一 } 函数
2 2
C.已知函 =数 =的(定 义) 域为 ,则函数 的定义域为
D.若函数 (2 +1) ,[则−1,1] ( ) [−1,3]
2
10.下列叙 述( 正 确−的1)是=( −) 3 ( )= − −2( ≥−1)
A.甲、乙、丙等 人排成一列,若甲与丙不相邻,则共有 种排法
B.用数字 , ,5, 这四个数可以组成没有重复数字的四3位6数共有 个
C. 个人分0别1从 2个3景点中选择一处游览,有 种不同选法 18
D.4正十二边形的对3 角线的条数是 81
11.已知函数 与 的定义域均54为 ,且 , ,若 的图象
关干点 对 (称 ),则 (( )) ( )+ (1− )=3 ( )+ ( −3)=3 = ( )
A. (1,0) B.
(0)=3 (− )= ( )
C. 是奇函数 D.
2025
三、 ( 填 + 空 2 题 ) :本题共3小题,每小题5分,共15 �分 = 。 1 ( )=0
12.在 的展开式中,常数项为______ 用数字作答
1 6
( + ) .( )
13.若函数 是定义在 上的增函数,则实数 的取值范围是______.
2
−( −1) +1, ≥2
( )=
14.甲、乙两名同学
(
参
3
加
+
汉
2)
语
听
−
写
3,
比
<
赛
2
,每次由其中一人听写,规则如下:若听写正确则此人继续听写,若
未听写正确则换对方听写,无论之前听写情况如何,甲每次听写的正确率均为 ,乙每次听写的正确率均
为 ,第 次听写的人是甲、乙的概率各为 ,则第二次听写的人是甲的概率0.6______;第 次听写的人是
甲的0.8概率__1____. 0.5
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
第 页,共 页
2 815. 本小题 分
已知(函数 13 ) .
3 2
求函数 ( )=在 −3 处切−线9 的+方1程;
(1)求函数 ( )的极 =值0.
(126). 本小题 ( ) 分
为了(研究高中15学生)平时的数学成绩和整理数学错题习惯的情况,某校数学建模兴趣小组的同学在本校抽取
名学生进行调查统计,数据如表:
1整00理数学 数学成绩
合计
错题习惯 优秀 非优秀
有
没有 20 30 50
合计 10 40 50
依据小概率值 30的独7立0性检验10,0是否认为数学成绩优秀与整理数学错题集习惯有关联;
(1)在调查统计有整 =理0数.0学5错题集习惯的 名学生中,采用比例分配的分层随机抽样的方法选取 人组建
(研2)讨小组,再从 人研讨小组中随机抽取50 人进行访谈,用 表示访谈时成绩优秀的人数,求 的5分布列及
数学期望. 5 3
附: ,
2 ( − )
=( + )( + )( + )( + )
2
( ≥ ) 0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
17. 本小题 分
已知(函数 15 ) .
求 的( 单)=调(区 间+及2)最 值;
(1)求出 ( 方)程 的解的个数.
(128). 本小题 ( 分)= ( ∈ )
已知(定义域都17为 )的函数 与 满足: 是偶函数, 是奇函数,且 .
求函数 、 的解 (析 )式; ( ) ( ) ( ) ( )+ ( )=2⋅3
(1)直接说明 ( 函)数 ( )的单调性,并解关于 不等式: ;
2
(2) ( ) ( +4 )+ ( −6)> 0
第 页,共 页
3 8设 , ,对于 ,都有 ,使得 ,
3 −2
(求3)实数 ( 的)=取3值 +范2 围ℎ(. )= (2 )−2 ( )+2 −3 ∀ 1 ∈ ∃ 2 ∈[0,+∞) ( 1)= ℎ( 2)
19. 本小 题 分
( 17 )
设随机变量 的概率分布为 , ,其中 是大于 的常数, 为自然对数的底数则称
−
服从参数为 的泊松分布,记 (为 =~ )= . ! ∈ 0 .
若 , 求 ; ( )
(1)已知 =当2 ,( =1) 时,可以用泊松分布近似二项分布,即对于 ~ , ~ ,有
(2) ≥2请0用0泊<松 分≤布0.近05似二项分布解决下列问题:若 ~ , ( , ) , ( ) ( =,
212
求)实≈数 ( 的=取 值).范围; (20, ) 0< ≤0.05 ( ≤ 2)> 223
若 ~ , ~ ,且 , 的任意取值均相互独立,记 ,试判断随机变量 是否服
(从3)泊松 分1 布 ,( 1如)果 服2从 ,( 请2)求出泊 1松分 2布对应的参数,如果不服从, 请=说 1明+理 由2 .
参考数据: .
0.8
=2.23
第 页,共 页
4 8参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10 .
11.
12.
20
13.
2 3
(−3,4]
14.
21 2 −1 1
15.56× 因 ( 为5函 ) 数 +3 ,所以求导得 ′ .
3 2 2
所以(1)′ (又 )= −3, −9 +1 ( )=3 −6 −9
所以函 数(0在)=−9.处的 (0切)线=方1程为 ,即 .
因为 ′ =0 −1=−9( −0) 9 + −.1=0
2 2
(令2) ,( 解)=得3 −6或 −9=3.( −2 −3)=3( −3)( +1)
当 ( )=或0 时=,3 ′ =−1 ;当 时, ′ .
所以 >3 在 <−1 , ( )>0上单调−递1增<, <在3 上单( )调<递0减.
所以 ( )的极(−大∞值,−为1) (3,+∞) (,−极1,小3)值为 .
3 2
16. (零 )假设 :数 学(成−绩1)优=秀−与1−整3理+数9学+错1题=集6习惯无关, (3)= 3 −3×3 −9×3+1=−26
(1) 0
由列联表中的数据可得 ,
2
2 100×(20×40−10×30)
依据小概率值 的=独立性30检×7验0×,50我×5们0推断≈4.不76成2立>,3.841= 0.05
即认为数学成绩 优=秀0.0与5整理数学错题集习惯有关联 ,0 此推断犯错误的概率不超过 ;
0.05
由分层抽样可知, 人研讨小组中,成绩非优秀的人数为 人,成绩优秀的人数为
30 20
(2) 5 5×50=3 5×50=2
第 页,共 页
5 8人,
由题意可知,随机变量 的可能取值有 、 、 ,
0 1 2
, , ,
3 2 1 2 1
3 1 3 2 3 2 3 3
故 ( 随 = 机 0 变 ) 量 = 的5 3 = 分1布0 列 如 ( 下 = 表 1 所 )= 示: 5 3 =5 ( =2)= 5 3 =10
0 1 2
1 3 3
所以,10 5 . 10
1 3 3 6
17. 由 (题 )设= ′ 0×10+1×5+2,×故10=5 时, ′ , 时, ′ ,
所以 (1) 在 ( )=上( 单+调3)递 减,在 <−3 上单( 调)递<增0 , 且 >−3 ( )>0 ,
1
( ) (−∞,−3) (−3,+∞) ( )≥ (−3)=− 3
当 时, , 时, ,故 .
1
→−∞ ( )→ 0 →+∞ ( )→+∞ ( )∈ [− 3,+∞)
综上, 的递减区间为 ,递增区间为 ,最小值为 ,无最大值;
1
由 (分 )析,可得 的(−大∞致,图−象3)如下: (−3,+∞) − 3
(2) (1) ( )
当 时, 无解;
1
<− 3 ( )=
当 时, 有两个不同解;
1
− 3 < <0 ( )=
当 或 时, 有且仅有一个解.
1
18 . =− 由 题 3 设 , ≥ 0 ( )= 且 ,
−
所以(1) (−, )+ (− )= ( )− ( )=2⋅3 ( )+ ( )=2⋅3
−
两式相 ( 减)可=得3 +3 ;
−
由 , ( )= 3 在−3上均单调递增,
−
(故2) 在=3上单 调=递−增3,
由 ( ) ,
2
则 ( +4 )+ ( −6)> 0 ,
2
( +4 )>− ( −6)= (6− )
第 页,共 页
6 8所以 ,
2
即 +4 >6− ,可得 或 ,
2
所以 解+集5 为−6=( +6)( −1)>;0 <−6 >1
(−∞,−6)∪(1,+∞)
时, ,
3 −2 4
(3) ∈ ( )= 3 +2=1−3 +2
因为 ,
4
故 0< 3 +2<2,
当 ( )∈时(,−1,1)
≥ 0 ℎ( )= (2 )−2 ( )+2 −3
2 −2 −
=3 +3 −2(3 −3 )+2 −3 ,
− 2 −
=令(3 −3 ) −,2则(3 −3,)+2 −1
−
则 =3 −3 ≥0 ,
2 2
由ℎ( )=, 都( )= −2 +2, 使−得1=( −1) +2, −2≥2 −2
1 ∈ ∃ 2 ∈[0,+∞) ( 1)= ℎ( 2)
只需 ,即 ,
1
2 −2≤−1 ≤2
所以实数 的取值范围为
1
(−∞,2].
19. 因为随机变量 的概率分布为 , ,
−
(1) ( = )= ! ∈
如果 ,那么可得 ;
1 −2
2 2
=2 ( =1)= 1! = 2
根据 ,
2
0 − 1 − 2 −
⋅ ⋅ ⋅ 1+ +2
(其2)中 ( ≤,2)= ( =.0)+ ( =1)+ ( =2)≈ 0! + 1! + 2! =
=20 0< ≤1
令函数 ,其中 ,那么导函数 ′ ,
2
2
1+ +2
因此函数 ( )=在区 间 上单0调<递 ≤减1, ( )=−2 <0
( ) (0,.1)
又因为 ,
0 82
1+0.8+ 2 212
(0.8)= 0.8 =223
因此对于不等式 ,它的解为 ,
2
1+ +2 212
即 , 所 以>223 ; 0< <0.8
0<20 <0.8 0< <0.04
根据题:
(3) ( = )= ( 1+ 2 = )= � =1 ( 1 = , 2 = − )
− 1 − − 2
1 2
=� ( 1 = ) ( 2 = − )= � ⋅
=1 =1 ! ( − )!
第 页,共 页
7 8
− −( 1+ 2)
− 2− 1 1 2 ! −
= � ⋅ = � ⋅ 1 2
=1 ! ( − )! ! =1 !( − )!
−( 1+ 2) −( 1+ 2)
−
= � ⋅ 1 2 = ( 1+ 2)
! =1 !
因此可得 ~ ,所以随机变量 服从泊松分布,对应的参数是 .
( 1+ 2) 1+ 2
第 页,共 页
8 8