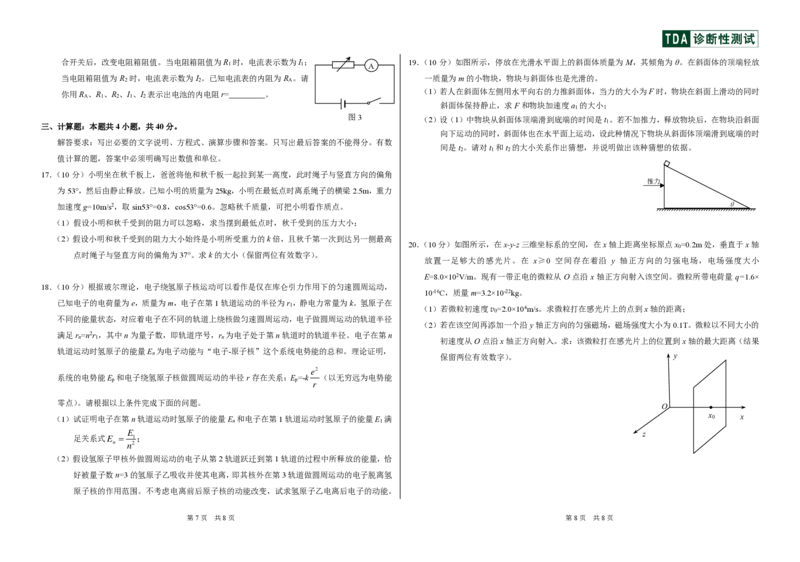文档内容
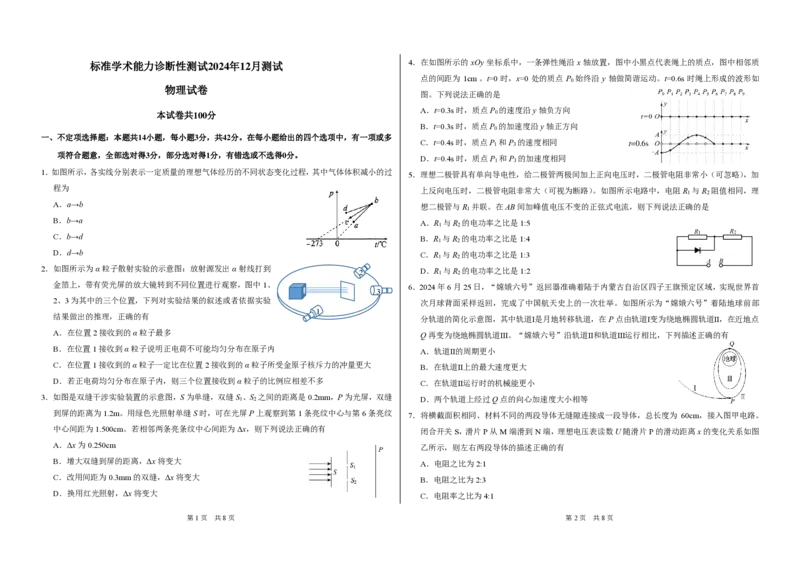
标准学术能力诊断性测试2024年12月测试 4.在如图所示的 xOy 坐标系中,一条弹性绳沿 x 轴放置,图中小黑点代表绳上的质点,图中相邻质
点的间距为 1cm.。t=0 时,x=0 处的质点 P 始终沿 y 轴做简谐运动。t=0.6s 时绳上形成的波形如
0
物理试卷
图。下列说法正确的是
A.t=0.3s时,质点P 的速度沿y轴负方向
本试卷共100分 0
B.t=0.3s时,质点P 的加速度沿y轴正方向
0
一、不定项选择题:本题共14小题,每小题3分,共42分。在每小题给出的四个选项中,有一项或多
C.t=0.4s时,质点P 1 和P 3 的速度相同 t=0.6s
项符合题意,全部选对得3分,部分选对得1分,有错选或不选得0分。
D.t=0.4s时,质点P 和P 的加速度相同
1 3
1.如图所示,各实线分别表示一定质量的理想气体经历的不同状态变化过程,其中气体体积减小的过
5.理想二极管具有单向导电性,给二极管两极间加上正向电压时,二极管电阻非常小(可忽略),加
程为
上反向电压时,二极管电阻非常大(可视为断路)。如图所示电路中,电阻R 与R 阻值相同,理
1 2
A.a→b
想二极管与R 并联。在AB间加峰值电压不变的正弦式电流,则下列说法正确的是
1
B.b→a
A.R 与R 的电功率之比是1:5
1 2
C.b→d
B.R 与R 的电功率之比是1:4
R1 R2
1 2
D.d→b
C.R 与R 的电功率之比是1:3
1 2
A B
2.如图所示为α粒子散射实验的示意图:放射源发出α射线打到
2 D.R 1 与R 2 的电功率之比是1:2
金箔上,带有荧光屏的放大镜转到不同位置进行观察,图中1、
6.2024年6月25日,“嫦娥六号”返回器准确着陆于内蒙古自治区四子王旗预定区域,实现世界首
3
2、3为其中的三个位置,下列对实验结果的叙述或者依据实验
次月球背面采样返回,完成了中国航天史上的一次壮举。如图所示为“嫦娥六号”着陆地球前部
1
结果做出的推理,正确的有
分轨道的简化示意图,其中轨道Ⅰ是月地转移轨道,在P点由轨道Ⅰ变为绕地椭圆轨道Ⅱ,在近地点
A.在位置2接收到的α粒子最多
Q再变为绕地椭圆轨道Ⅲ。“嫦娥六号”沿轨道Ⅱ和轨道Ⅲ运行相比,下列描述正确的有
B.在位置1接收到α粒子说明正电荷不可能均匀分布在原子内
A.轨道Ⅱ的周期更小
C.在位置1接收到的α粒子一定比在位置2接收到的α粒子所受金原子核斥力的冲量更大
B.在轨道Ⅱ上的最大速度更大
D.若正电荷均匀分布在原子内,则三个位置接收到α粒子的比例应相差不多
C.在轨道Ⅱ运行时的机械能更小
3.如图是双缝干涉实验装置的示意图,S为单缝,双缝S
1
、S
2
之间的距离是0.2mm,P为光屏,双缝
D.两个轨道上经过Q点的向心加速度大小相等
到屏的距离为1.2m。用绿色光照射单缝S时,可在光屏P上观察到第1条亮纹中心与第6条亮纹
7.将横截面积相同、材料不同的两段导体无缝隙连接成一段导体,总长度为 60cm,接入图甲电路。
中心间距为1.500cm。若相邻两条亮条纹中心间距为Δx,则下列说法正确的有
闭合开关S,滑片P从M端滑到N端,理想电压表读数U随滑片P的滑动距离x的变化关系如图
A.Δx为0.250cm
乙所示,则左右两段导体的描述正确的有
B.增大双缝到屏的距离,Δx将变大
A.电阻之比为2:1
C.改用间距为0.3mm的双缝,Δx将变大
B.电阻之比为2:3
D.换用红光照射,Δx将变大
C.电阻率之比为4:1
第1页 共8页 第2页 共8页
{#{QQABCQAAggAAQBJAABhCEwXgCACQkhECAagGBBAMMAAByAFABAA=}#}D.电阻率之比为4:3 A.I 沿GE方向
1
B.I 沿NM方向 2
C.电流I 不断减小
2
D.电流I 大小不变
2
12.重离子肿瘤治疗装置中的回旋加速器可发射某种重离子束,其电流强度为1.2×10-5A,在1s内发
射的重离子个数为1.5×1013,则单个重离子带电量为
A.8.0×10-19C B.6.4×10-19C C.4.8×10-19C D.3.2×10-19C
8.世界短跑名将博尔特百米的最大速度可达到12m/s,他的百米运动可简化为以某一加速度匀加速运 13.如图所示,一足够长的木板在水平地面上运动,在t=0时刻将一相对于地面静止的物块轻放到木
动达到最大速度后,以最大速度匀速跑完全程,如果某次训练中要求博尔特百米成绩在10秒以内, 板的右端,己知物块与木板的质量相等,物块与木板间及木板与地面间均有摩擦,物块与木板间
则他加速阶段的加速度至少为 的最大静摩擦力等于滑动摩擦力。在物块放到木板上之后,木板和物块运动的速度-时间图象可
A.3.0m/s2 B.3.2m/s2 C.3.6m/s2 D.4.0m/s2 能是
9.如图所示,旅客用双轮行李小车运送行李。若小车在拉运过程中角度不变,行李总质量为 20kg,
不计行李箱与小车之间的摩擦力,取g=10m/s2。在某一段行程中,旅客拉着小车以2m/s2的加速度
加速直线前进。取 sin53°=0.8,cos53°=0.6。下列对小车两个支撑面对行李箱的支持力的大小的判
定正确的有
A.F =136N
1
B.F =150N 1
C.F =152N
2
D.F =174N 14.把一段导体棒用细导线水平悬挂在竖直向上的匀强磁场间(图中未画出磁场),导体棒通过轻质细
2
10.如图所示,平行板电容器带有等量异种电荷,与静电计相连,静电计金属外壳和电容器下极板都 导线a、b接入恒定电流后开始向右侧摆动,经过时间t到达最高点,此时悬线偏离竖直方向的最
接地,在两极板间有一个固定在P点的点电荷,以E表示两板间的电场强度,E 表示点电荷在P 大摆角为θ,设磁场范围足够大。若导体棒的质量为m,单根悬线的长度为L,重力加速度为g,
p
点的电势能(设大地电势为0),θ表示静电计指针的偏角。若保持下极板不动,将上极板向下移 空气阻力不计。下列说法正确的是
动一小段距离至图中虚线位置,则 A.图中的a接电源正极
A.θ减小 B.E减小 B.导体棒受到的安培力等于
C.E 减小 .D.E 不变
p p
11.图中EF、GH为平行的金属导轨其电阻可不计,R为电阻器,C为电容器;AB为可在EF和GH
上滑动的导体横杆,其电阻可不计;有匀强磁场垂直于导轨平面。若用I 和I 分别表示图中该处
1 2
导线中的电流,则在横杆AB在轨道上向右匀减速运动过程中,下列描述正确的有
第3页 共8页 第4页 共8页
m g (1
s in
c o s )
+
E M A F
I I
1 2
V
0.6
U/V
R
C
x
P
0.4
G N B H
M N
0.2
S E R0 x/cm
0 20 40 60
甲 乙
v
0
v v v v
v 0 v 0 v 0 v 0
F F
1 2
v O t O t 1 t 1 t O t 1 t 1 t O t 1 t 1 t
A B C D
53° 37°
a
b
P L
C.摆动到最高点时,绳的拉力等于mg
D.导体棒从最低点摆动到最高点的过程中,受到绳的拉力的冲量大小
2mgt
等于
1+cos
{#{QQABCQAAggAAQBJAABhCEwXgCACQkhECAagGBBAMMAAByAFABAA=}#}二、实验题:本题共2小题,共18分。 F.开关、导线若干
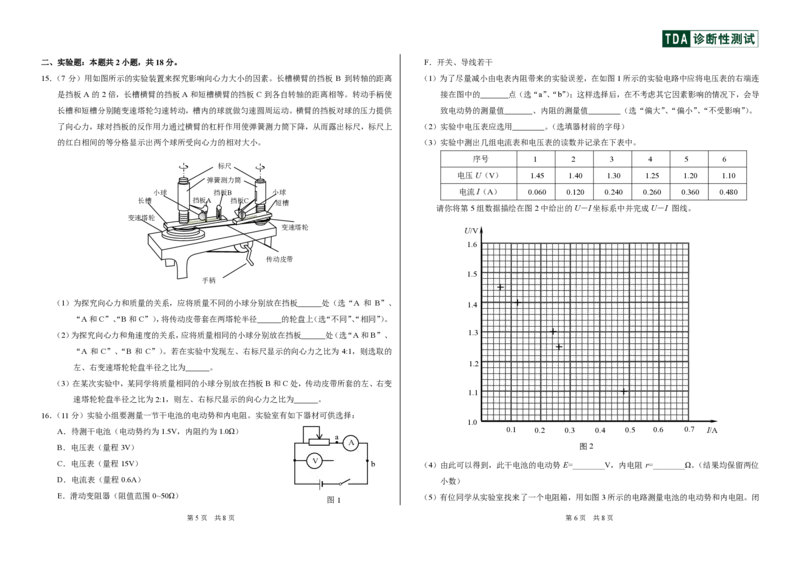
15.(7 分)用如图所示的实验装置来探究影响向心力大小的因素。长槽横臂的挡板 B 到转轴的距离 (1)为了尽量减小由电表内阻带来的实验误差,在如图1所示的实验电路中应将电压表的右端连
是挡板A的2倍,长槽横臂的挡板A和短槽横臂的挡板C到各自转轴的距离相等。转动手柄使 接在图中的 点(选“a”、“b”);这样选择后,在不考虑其它因素影响的情况下,会导
长槽和短槽分别随变速塔轮匀速转动,槽内的球就做匀速圆周运动。横臂的挡板对球的压力提供 致电动势的测量值 、内阻的测量值 (选“偏大”、“偏小”、“不受影响”)。
了向心力,球对挡板的反作用力通过横臂的杠杆作用使弹簧测力筒下降,从而露出标尺,标尺上 (2)实验中电压表应选用 。(选填器材前的字母)
的红白相间的等分格显示出两个球所受向心力的相对大小。 (3)实验中测出几组电流表和电压表的读数并记录在下表中。
序号 1 2 3 4 5 6
标尺
电压U(V) 1.45 1.40 1.30 1.25 1.20 1.10
弹簧测力筒
小球 挡板B 小球 电流I(A) 0.060 0.120 0.240 0.260 0.360 0.480
长槽 挡板A 挡板C 短槽
请你将第5组数据描绘在图2中给出的U-I坐标系中并完成U-I 图线。
变速塔轮
变速塔轮
U/V
1.6
传动皮带
1.5
手柄
+
(1)为探究向心力和质量的关系,应将质量不同的小球分别放在挡板 处(选“A 和 B”、 1.4 +
“A和C”、“B和C”),将传动皮带套在两塔轮半径 的轮盘上(选“不同”、“相同”)。
+
(2)为探究向心力和角速度的关系,应将质量相同的小球分别放在挡板 处(选“A和B”、 1.3
+
“A 和 C”、“B 和 C”)。若在实验中发现左、右标尺显示的向心力之比为 4:1,则选取的
1.2
左、右变速塔轮轮盘半径之比为 。
(3)在某次实验中,某同学将质量相同的小球分别放在挡板B和C处,传动皮带所套的左、右变
+
1.1
速塔轮轮盘半径之比为2:1,则左、右标尺显示的向心力之比为 。
16.(11分)实验小组要测量一节干电池的电动势和内电阻。实验室有如下器材可供选择:
1.0
A.待测干电池(电动势约为1.5V,内阻约为1.0Ω) 0.1 0.2 0.3 0.4 0.5 0.6 0.7 I/A
a
A
B.电压表(量程3V) 图2
C.电压表(量程15V) V b (4)由此可以得到,此干电池的电动势 E=________V,内电阻 r=________Ω。(结果均保留两位
D.电流表(量程0.6A) 小数)
E.滑动变阻器(阻值范围0~50Ω)
图1
(5)有位同学从实验室找来了一个电阻箱,用如图3所示的电路测量电池的电动势和内电阻。闭
第5页 共8页 第6页 共8页
{#{QQABCQAAggAAQBJAABhCEwXgCACQkhECAagGBBAMMAAByAFABAA=}#}合开关后,改变电阻箱阻值。当电阻箱阻值为R 时,电流表示数为I ;
1 1
当电阻箱阻值为 R 时,电流表示数为 I 。已知电流表的内阻为 R 。请
2 2 A
你用R 、R 、R 、I 、I 表示出电池的内电阻r= 。
A 1 2 1 2
三、计算题:本题共4小题,共40分。
解答要求:写出必要的文字说明、方程式、演算步骤和答案。只写出最后答案的不能得分。有数
值计算的题,答案中必须明确写出数值和单位。
17.(10 分)小明坐在秋千板上,爸爸将他和秋千板一起拉到某一高度,此时绳子与竖直方向的偏角
为53°,然后由静止释放。已知小明的质量为25kg,小明在最低点时离系绳子的横梁2.5m,重力
加速度g=10m/s2,取sin53°=0.8,cos53°=0.6。忽略秋千质量,可把小明看作质点。
(1)假设小明和秋千受到的阻力可以忽略,求当摆到最低点时,秋千受到的压力大小;
(2)假设小明和秋千受到的阻力大小始终是小明所受重力的k倍,且秋千第一次到达另一侧最高
点时绳子与竖直方向的偏角为37°。求k的大小(保留两位有效数字)。
18.(10 分)根据玻尔理论,电子绕氢原子核运动可以看作是仅在库仑引力作用下的匀速圆周运动,
已知电子的电荷量为e,质量为m,电子在第1轨道运动的半径为r ,静电力常量为k。氢原子在
1
不同的能量状态,对应着电子在不同的轨道上绕核做匀速圆周运动,电子做圆周运动的轨道半径
满足r =n2r ,其中n为量子数,即轨道序号,r 为电子处于第n轨道时的轨道半径。电子在第n
n 1 n
轨道运动时氢原子的能量E 为电子动能与“电子-原子核”这个系统电势能的总和。理论证明,
n
e2
系统的电势能E 和电子绕氢原子核做圆周运动的半径r存在关系:E =-k (以无穷远为电势能
p p
r
零点)。请根据以上条件完成下面的问题。
(1)试证明电子在第n轨道运动时氢原子的能量E 和电子在第1轨道运动时氢原子的能量E 满
n 1
足关系式
第7页 共8页 第8页 共8页
E
n
=
E
n
12 ;
19.(10 分)如图所示,停放在光滑水平面上的斜面体质量为 M,其倾角为 θ。在斜面体的顶端轻放
A
一质量为m的小物块,物块与斜面体也是光滑的。
(1)若人在斜面体左侧用水平向右的力推斜面体,当力的大小为F时,物块在斜面上滑动的同时
斜面体保持静止,求F和物块加速度a 的大小;
1
图3
(2)设(1)中物块从斜面体顶端滑到底端的时间是t 。若不加推力,释放物块后,在物块沿斜面
1
向下运动的同时,斜面体也在水平面上运动,设此种情况下物块从斜面体顶端滑到底端的时
间是t 。请对t 和t 的大小关系作出猜想,并说明做出该种猜想的依据。
2 1 2
推力
θ
20.(10分)如图所示,在x-y-z三维坐标系的空间,在x轴上距离坐标原点x =0.2m处,垂直于x轴
0
放置一足够大的感光片。在 x≥0 空间存在着沿 y 轴正方向的匀强电场,电场强度大小
E=8.0×102V/m。现有一带正电的微粒从 O 点沿 x 轴正方向射入该空间。微粒所带电荷量 q=1.6×
10-16C,质量m=3.2×10-22kg。
(1)若微粒初速度v =2.0×104m/s。求微粒打在感光片上的点到x轴的距离;
0
(2)若在该空间再添加一个沿y轴正方向的匀强磁场,磁场强度大小为0.1T。微粒以不同大小的
初速度从O点沿x轴正方向射入。求:该微粒打在感光片上的位置到x轴的最大距离(结果
保留两位有效数字)。 y
O
x 0 x
z
(2)假设氢原子甲核外做圆周运动的电子从第2轨道跃迁到第1轨道的过程中所释放的能量,恰
好被量子数n=3的氢原子乙吸收并使其电离,即其核外在第3轨道做圆周运动的电子脱离氢
原子核的作用范围。不考虑电离前后原子核的动能改变,试求氢原子乙电离后电子的动能。
{#{QQABCQAAggAAQBJAABhCEwXgCACQkhECAagGBBAMMAAByAFABAA=}#}标准学术能力诊断性测试 2024 年 12 月测试
物理参考答案
一、不定项选择题:本题共14小题,每小题3分,共42分。在每小题给出的四个选项中,
有一项或多项符合题意,全部选对得3分,部分选对得1分,有错选或不选得0分。
1 2 3 4 5 6 7 8 9 10
AC BC BD AD A BD AC C AC AD
11 12 13 14
BD A BD CD
二、实验题:本题共2小题,共18分。
15.(7分)
(1)A和C(1分) 相同(1分)
(2)A和C(1分) 1:2(2分)
(3)1:2(2分)
16.(11分)
(1)b(1分) 偏小(1分) 偏小(1分)
(2)B(1分)
(3)图略(2分:描点、连线各1分)
(4)1.50(1.49~1.51)(1分) 0.83(0.82~0.84)(2分)
I R −I R
(5) 1 1 2 2 −R (2分)
I −I A
2 1
三、计算题:本题共4小题,共40分。
17.(10分)
(1)从开始释放到最低点的过程中:mgL(1-cos53°)=
第1页 共4页
1
2
mv2(2分)
mv2
=N-mg(2分)
L
带入数值计算可得N=450N(1分)
根据牛顿第三定律,压力等于支持力,大小为450N。(1分)
(2)从释放到另一侧最高点过程,对小明有:
mgL(cos37°-cos53°)=kmg×L× (2分)
2
{#{QQABCQAAggAAQBJAABhCEwXgCACQkhECAagGBBAMMAAByAFABAA=}#}k=0.13(2分)
18.(10分)
(1)设电子在第1轨道上运动的速度大小为v ,根据牛顿第二定律有
1
e2 v2
k =m 1 (1分)
r2 r
1 1
电子在第1轨道运动的动能
第2页 共4页
E
1k
=
1
2
m v 21 =
k
2
2 e
r1
(1分)
e2 ke2
电子在第1轨道运动时氢原子的能量E = -k + =- k
1
r 2r
1 1
e
2
2
r1
(1分)
同理,电子在第n轨道运动时氢原子的能量E =-k
n
2 e
rn
+
k
2
2 e
rn
=-k
e
2
2
rn
(1分)
又因为 r =n2r ,则有E =-k
n 1 n
e
2
2
rn
=-k
2
e
n
2
2 r1
=
E
n
12 ,命题得证。 (1分)
(2)由(1)E =- k
1
e
2
2
r1
、E
n
=
E
n
12
电子在第2轨道运动时氢原子的能量E =
2
E
2
12
e2
=-k (1分)
8r
1
电子从第2轨道跃迁到第1轨道所释放的能量ΔE= E
2
− E
1
=
3 k
8
e
r1
2
(1分)
E
电子在第3轨道运动时氢原子的能量E = 1 =-k
3
32 1
e
8
2
r1
(1分)
设氢原子电离后电子具有的动能为E ,根据能量守恒有
k
E = E +ΔE(1分)
k 3
解得E =
k
k
2
7
3
2
2 e
r1
(1分)
19.(10分)
(1)斜面体和物块的受力情况如图1所示
对物块:垂直于斜面方向F =mgcosθ(1分) 沿斜面方向mgsinθ=ma (1分)
N 1
由于冰车保持静止,有:F=F sinθ(1分)
N
解得:a =gsinθ(1分) F= mgcosθsinθ(1分)
1
{#{QQABCQAAggAAQBJAABhCEwXgCACQkhECAagGBBAMMAAByAFABAA=}#}(2)t >t 。(1分)
1 2
法一:设两种情况下物块的位移分别为l 、l ,如图2所示,有l >l (1分)
1 2 1 2
若不加推力:如图3,由l 的方向可知,物块在沿斜面和垂直于斜面向下均有加速度,
2
且其分加速度a =a =gsinθ(1分)
2x 1
故a > a (1分)
2 1
根据l=
第3页 共4页
1
2
at2(1分),可判定t >t 。
1 2
仅提出因第二种情况下斜面体运动导致物块运动时间短,但未能做出理论分析不得分;
法二:利用答图2中位移关系l >l(1分),将运动沿斜面和垂直于斜面方向分解:得
1 2
x >x (1分)
1 2
如图 3,物块在沿斜面和垂直于斜面向下均有加速度,且其分加速度 a =a =gsinθ(1
2x 1
分)
根据公式x=
1
2
at2(1分),可判定t >t 。
1 2
法三:a =a =gsinθ(1分);故a > a (1分,无此式后面不赋分)
2x 1 2 1
与竖直方向的夹角β >β ,两次物块的加速度的竖直分量a > a (1分)。
2 1 2y 1y
1
根据h= a t2(1分),可判定t >t 。
y 1 2
2
20.(10分)
(1)设带电微粒在电场中运动时间为t ,打在感光片上的点到x轴的距离为y ,则
1 1
qE x
a= (1分) t = 0 (1分)
1
m v
0
y =
1
1
2
FN
F
地
mg F
θ
l
1
FN Mg θ
答图1 答图2 l 2
a
2y
a
2x
a
2
答图3
a t2(1分)得:y =0.02m(1分)
1 1
(2)当粒子在xz平面内做匀速圆周运动的轨迹与感光片相切时该微粒的z坐标最大。
此时:z = x (1分)
m 0
且此时:
2 2m
粒子在xz平面内做匀速圆周运动满足由qvB=m( )2R 得:T = ,恒定。
T qB
如图,设粒子在xz平面内做匀速圆周运动圆心角为θ,则从出发到达到感光片上的时
{#{QQABCQAAggAAQBJAABhCEwXgCACQkhECAagGBBAMMAAByAFABAA=}#}间t=
第4页 共4页
2
T
;
即圆心角越大,运动时间越长。
则当粒子恰好与感光片相切时(θ=
2
),时间t最长,y值最大。
(以上论证共2分)
1 m
t = T = (1分)
m
4 2qB
1
故y = at 2=0.20m(1分)
m m
2
故离x轴的最大距离d= z
m
2 + y
m
2
屏
O
x
x 0
R
θ
z
=0.28m(1分)
{#{QQABCQAAggAAQBJAABhCEwXgCACQkhECAagGBBAMMAAByAFABAA=}#}