文档内容
.
高中数学公式
第一部分:集合、条件、不等式
⑴常用数集:正整数集N(N ),自然数集N ,整数集Z,有理数集Q,实数集R。
1、集合 ⑵子集(包括真子集和相等)、交集、并集、补集、全集、空集(是任何集合的子集,是任何非空集合的真子集)
⑶含n个元素的集合个数:子集有2n个;真子集有2n-1个;非空子集有2n-1个;非空真子集有2n-2个.
定义:可以判断真假的陈述句叫命题。
四种命题:①原命题:若p则q; ②逆命题:若q则p;
2、命题
③否命题:若p则q; ④逆否命题:若q则p
注:原命题与逆否命题同真假;逆命题与否命题同真假。四种命题的真假个数:0个,2个,4个
① p是q的充分不必要条件(p是q的真子集) ② p是q的必要不充分条件(q是p的真子集)
3、条件
③ p是q的充要条件 (p = q相等) ④ p是q的既不充分也不必要条件(p、q互不包含)
技巧:小范围推大范围,大范围不能推小范围,即小的推大的,大的不能推小的
⑴逻辑联词或且非,或命题一真就真,且命题全真才真,非命题真假互换。
4、逻辑连 ①且(交集): pq; ②或(并集): pq; ③非(结论否定):p .
词、量词
⑵量词一般有两个,全称量词所有的,存在量词有一个,若要否定变形式。全称命题 p:x;特称命题p:x;
两项:⑴ 直接开平方;(形如x2 1) ⑵ 提取公因式;(形如x2 2x 0);
b b2 4ac
三项:⑶ 十字相乘法;⑷ 配方法(提;配;括;完) ⑸公式法:求根公式:x
5、二次方 2a
程 b
判别式b24ac:韦达定理:
x
1
x
2
a
x x c
1 2 a
a
>1⇔a>b
b
a-b>0⇔a>b
a
两个实数比较大小的方法:(1)作差法:与0比a-b=0⇔a=b (2)作商法:与1比 =1⇔a=b (b>0)
b
6、不等式
a-b<0⇔ab a>b a>b a>b>0
(1)乘法 ⇒ac>bc ⇒acb+d (3)同向相乘 ⇒ac>bd
c>0 c<0 c>d c>d>0
第 1 页 共 22 页.
⑴ ax2+bx+c>0的解集{x| x x 或x x } “大于取两边”
1 2
7、二次不 ⑵ ax2+bx+c<0的解集{x| x x x } “小于取中间”
1 2
等式
a 0 a 0
若f(x)=ax2+bx+c (a≠0),则当 时,f(x)>0恒成立;当
时,f(x)<0恒成立.
Δ 0 Δ0
一般式:f(x)=ax2+bx+c
(a≠0)
方法:⑴ 配方法,顶点式:f(x)=a(x-m)2+n 对称轴x=m;顶点(m,n)
8、二次函
数
⑵ 十字相乘法,交点式:f(x)=a(x-x
1
)(x-x
2
) 与x轴的交点:x=x
1、
x
2
⑶ 对称轴方程:x b x 1 x 2 顶点坐标:( b , 4acb2 )
2a 2 2a 4a
f(x) f(x)
9、分式不 (1) >0 ⇔ f(x)·g(x)>0. (2) ≥ 0 ⇔ f(x)·g(x) ≥ 0且g(x)≠0.
g(x) g(x)
等式
f(x) f(x)
(3) <0 ⇔ f(x)·g(x)<0. (4) ≤ 0 ⇔ f(x)·g(x) ≤ 0且g(x)≠0.
化整式 g(x) g(x)
若a>0, ⑴ x a a x a “小于取中间”
10、绝对值 ⑵ x a x a 或 x a “大于取两边”
不等式
若c>0, ⑴ |ax+b| < c -c < ax+b < c;
⑵ |ax+b| > c ax+b>c或ax+b <-c
第二部分:函数、导数
根式运算: a b ab; a a a b ab 整数幂:⑴an aaa(n个a相乘) ⑵an 1 ⑶
b b b b b an
1、指数运 a0 1(a0) 分数幂:⑴ an 1 na ⑵ a m n nam ⑶a m n 1
算 nam
指数运算:aman amn;am
amn;abm ambm;(am)n amn
an
⑴ 指数与对数互化:xlog N ax N(a0,a1,N 0)
a
⑵ 对数恒等式:⑴log 10 ⑵log a1 ⑶ alog a N N ⑷log aN=N (指对之后还是N)
a a a
⑶ 常用对数:lgN =log N;自然对数:lnN=log N (e 2.7)
10 e
2、对数运
算 ⑷ 对数的运算: ① 加乘:log M log N log (MN) ② 减除:log M log N log M
a a a a a a N
n
③ 顶在外:log bn nlog b ④ 顶在外,体位不变:log bn log b
a a am m a
log b
⑤ 体位不变:log b c (学名换底公式,常用在对数的乘法运算中,但不常用)
a log a
c
第 2 页 共 22 页.
3、函数的 1
⑴分式: (x≠0) ⑵偶次方根:√𝑥 (𝑥≥0) ⑶零指数幂:𝑥0 (𝑥≠0) 𝑥−𝑛 (𝑥≠0) ⑷对数:log 𝑥 (𝑥>0)
𝑎
定义域 x
求函数解析式的4种方法
4、函数的
1
解析式 (1)换元法(从前到后)(2)配凑法(从后到前)(3)待定系数法.(4)解方程组法:f(x)与f( ) f(-x)解方程组.
x
设x、x [a,b],那么
1 2
f(x )-f(x )
⑴ 若x x,f(x ) f(x ) 0 f(x)为增函数;若 1 2>0 ⇔ f(x)为增函数 (同号为增)
5、函数的 1 2 1 2 x 1 -x 2
单调性 f(x )-f(x )
⑵ 若x x,f(x ) f(x ) 0 f(x)为减函数;若 1 2<0 ⇔ f(x)是减函数 (异号为减)
1 2 1 2 x-x
1 2
复合函数f(g(x))的单调性:f(u)、u=g(x) “同增异减”
偶函数:⑴ 定义域关于原点对称 ⑵ f(x) f(x) 偶函数图象关于y轴对称。
6、函数的
奇函数:⑴ 定义域关于原点对称 ⑵ f(x)f(x) 奇函数图象关于原点对称。
奇偶性
公共定义域内有:奇±奇=奇,偶±偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇.
ab
对称轴:f(a+x)=f(a-x) ⇔ f(x)图像关于直线x=a对称. f(a+x)=f(b-x) ⇔ 对称轴x
7、函数的 2
对称性 ab
对称中心:f(a+x)+f(a-x)=2b ⇔ f(x)图像关于点(a,b)对称. f(a+x)+f(b-x)=0 ⇔ 对称中心( ,0)
2
1 1
(1)f(x+a)=f(x),T=a. (2) f(x+a)=-f(x),T=2a. (3) f(x+a)= ,T=2a. (4) f(x+a)=- ,T=2a.
f(x) f(x)
1
(5)f(a+x)=f(b+x),T=ab.(6) 两个对称轴是半个周期 T:f(x)关于直线x=a,x=b对称,那么T=2ab.
8、函数的 2
周期性 1
(7) 两个对称中心也是半个周期 T:f(x)关于点(a,0)(b,0)对称,那么T=2ab.
2
1
(8) 对称轴与对称点是 个周期:f(x)关于直线x=a、点(b,0)对称,那么T=4ab. 三角函数图像可证明678
4
(1)一次函数:y kx b (k≠0) k:斜率 b:y轴上的截距 ①k>0,递增;②k<0,递减。
(2)二次函数:y=ax2+bx+c (a≠0) ①看a;②看Δ;③画图;④求解
9、常见的 (3)三次函数:y ax3 bx2 cx d 求导
五种函数
k
(4)反比例函数:y (k≠0) ①k>0,图像在一、三象限;②k<0,图像在二、四象限。
x
a
(5)双勾函数:y x (a>0) ①x>0,当x= a时,y min =2 a;②x<0,当x= a 时,y max = 2 a
x
第 3 页 共 22 页.
a b a2 b2
10、基本不 ⑴ab2 ab;a2 b2 2ab; ⑵ ab ( )2
2 2
等式
满足三个条件:“一正二定三相等” 口诀:ab≤均值的平方≤平方的均值 .
方程f(x)=0有实数根⇔函数y=f(x)的图象与x轴有交点⇔函数y=f(x)有零点.
函数零点存在性定理:函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)<0,则存在零点.函数单调,则存在一个零点。
11、零点问
函数零点个数的判断方法:(1)直接求零点;
题
(2)利用零点存在性定理,再结合函数的单调性确定零点个数;
(3)利用函数图象的交点个数判断
幂函数定义:形如y=xα 的函数称为幂函数
当α>0时,y=xα在[0,+∞)上为增函数 当α<0时,y=xα在(0,+∞)上为减函数.
1
性质 y=x y=x2 y=x3 1 y= =x1
y x x2
x
函数
图象
12、幂函数
定义域:x左右 R R R {x|x≥0} {x|x≠0}
值域:y上下 R {y|y≥0} R {y|y≥0} {y|y≠0}
奇偶性 奇 偶 奇 非奇非偶 奇
(-∞,0)减 (-∞,0)和
单调性 增 增 增
(0,+∞)增 (0,+∞)减
公共点 (1,1)
指数函数
①a>1 ②00时,y > 1; 当x> 0时,0 < y < 1;
性质
当x<0时,0 < y < 1 当x < 0时,y > 1
在(-∞,+∞)上是增函数(同号) 在(-∞,+∞)上是减函数(异号) c>d>1>a>b
第 4 页 共 22 页.
对数函数
①a>1 ②01时,y>0; 当x>1时,y<0;
性质
当00
在(0,+∞)上是增函数(同号) 在(0,+∞)上是减函数(异号) 00,右侧f′(x)<0,那么f(x)是极大值;
0 0
②如果在x 附近的左侧f′(x)<0,右侧f′(x)>0,那么f(x)是极小值
0 0
6、函数的最值
①连续函数f(x)在闭区间[a,b]上必有最大值与最小值.
②将函数的极值与端点处的值f(a),f(b)比较,最大的为最大值,最小的为最小值.
第 6 页 共 22 页.
第三部分:三角函数(公式、图像、解三角形)
1、
⑴ 角的概念:任意角的定义;正角(逆)、负角(顺)、零角;象限角轴上角;终边相同的角(代表+周期)
角的概念
与弧度制 ⑵ 角度制与弧度制的互化: 180 ,1 57
⑴ 圆的周长c 2 r;圆的面积S r2
2、
扇形弧长 ⑵ 扇形的弧长公式:𝒍=|𝜶|𝒓;
扇形面积
⑶ 扇形面积公式:𝑺= 𝟏 𝒍𝒓= 𝟏|𝜶|𝒓𝟐.
𝟐 𝟐
⑴ 三角函数的定义:角终边上任一点P(x,y),设|OP|r
则:sin 对 y cos 邻 x tan 对 y
斜 r 斜 r 邻 x
⑵ 三角函数的符号:一全正,二正弦,三正切,四余弦
⑶ 特殊角的三角函数值:(单位圆或查表)
3、三角函 角度 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°
数的定义 弧度 𝜋 𝜋 𝜋 𝜋 2𝜋 3𝜋 5𝜋 3𝜋
0 𝜋 2𝜋
6 4 3 2 3 4 6 2
sin α 1 √2 √3 √3 √2 1
0 1 0 −1 0
2 2 2 2 2 2
cos α √3 √2 1 1 √2 √3
1 0 − − − −1 0 1
2 2 2 2 2 2
tan α √3 √3
0 1 √3 不存在 −√3 −1 − 0 不存在 0
3 3
⑴ sin2θ+cos2θ=1 知一求二sinθ、cosθ、tan θ;平方搭桥(sin α±cos α)2=1±2sin αcos α;
4、同角关
sin θ
系式 ⑵ tan θ= . 弦切互化(分式齐次,分子分母同除以cosθ)
cos θ
⑴ 诱导公式的作用:化简大角化小角,负角化正角,最好化成特殊角.
5、
⑵ 谨记:出现轴上角才用诱导公式
诱导公式
⑶ 口诀:“奇变偶不变,符号看象限”
⑴S :sin(α±β)=sinα cosβ ± cosα sinβ; ⑵C :cos(α±β)=cosα cos β ∓ sinα sinβ;
α±β α±β
6、两角和 tan α±tan β
⑶T :tan(α±β)= .
α±β 1∓tan αtan β
差
配角技巧:所求角表示为已知角和特殊角的和、差、倍的形式。
第 7 页 共 22 页.
⑴ sin22sincos. ⑵cos2cos2sin22cos2112sin2.
7、二倍角、
2tan 1cos2 1cos2
降幂公式 ⑶tan2 . 降幂公式: cos2 ;sin2 .
1tan2 2 2
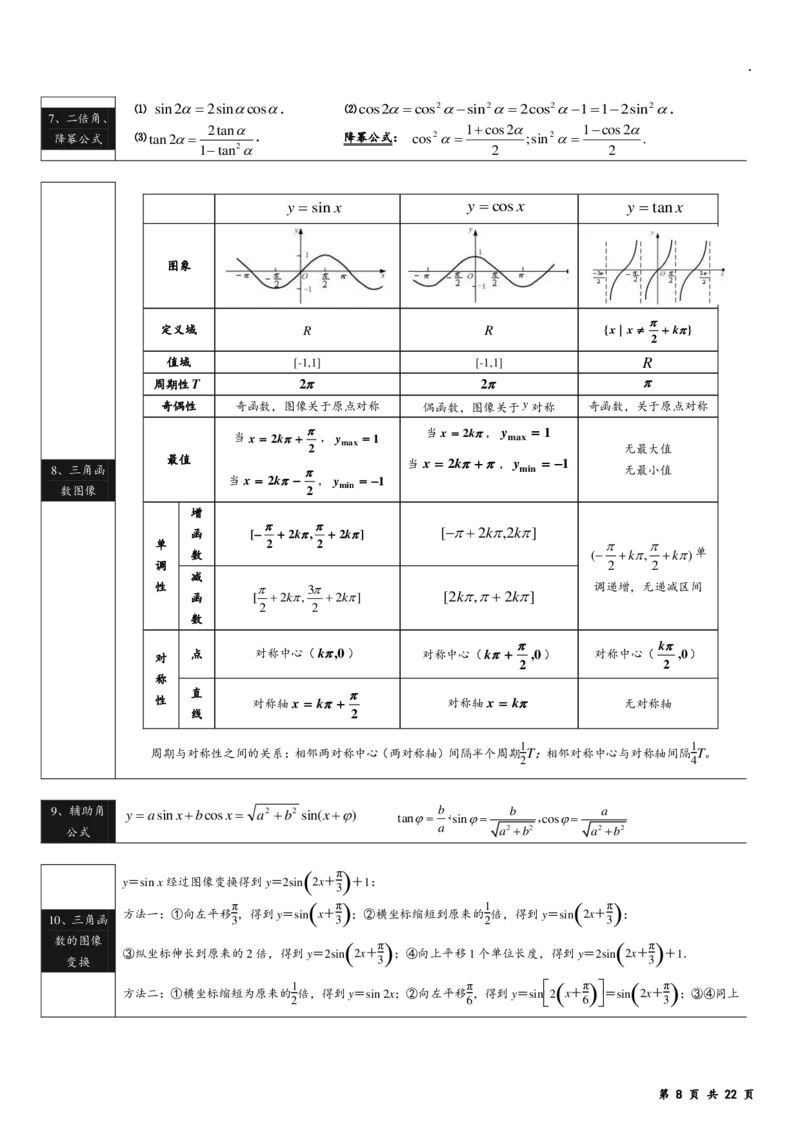
y sinx y cosx y tanx
图象
定义域 R R {x| x k}
2
值域 [-1,1] [-1,1] R
周期性T 2 2
奇偶性 奇函数,图像关于原点对称 偶函数,图像关于y对称 奇函数,关于原点对称
当x 2k ,y 1 当x 2k, y max 1
2 max 无最大值
最值
当x 2k,y 1
8、三角函 min 无最小值
当x 2k ,y 1
数图像 2 min
增
函 [ 2k, 2k] [2k,2k]
单 2 2
数 ( k, k)单
调 2 2
减
性 3 调递增,无递减区间
函 [ 2k, 2k] [2k,2k]
2 2
数
k
对 点 对称中心(k,0) 对称中心(k ,0) 对称中心( ,0)
2 2
称
直
性 对称轴x k 对称轴x k 无对称轴
线 2
1 1
周期与对称性之间的关系:相邻两对称中心(两对称轴)间隔半个周期 T;相邻对称中心与对称轴间隔 T。
2 4
9、辅助角 yasinxbcosx a2 b2 sin(x) tan其 b 中, sin b ,cos a
公式 a a2b2 a2b2
( π)
y=sin x经过图像变换得到y=2sin 2x+ +1:
3
π ( π) 1 ( π)
方法一:①向左平移 ,得到y=sin x+ ;②横坐标缩短到原来的 倍,得到y=sin 2x+ ;
10、三角函 3 3 2 3
数的图像
( π) ( π)
③纵坐标伸长到原来的2倍,得到y=2sin 2x+ ;④向上平移1个单位长度,得到y=2sin 2x+ +1.
变换 3 3
1 π ( π) ( π)
方法二:①横坐标缩短为原来的 倍,得到y=sin 2x;②向左平移 ,得到y=sin 2 x+ =sin 2x+ ;③④同上
2 6 6 3
第 8 页 共 22 页.
M-m M+m 2π
(1)A= ,(2)B= . (3)ω:先求周期T,再由T= 得ω.
2 2 ω
把A、B、ω代入y=Asin(ωx+φ)+B中
11、三角函
(4)φ:代特殊点:上升点(2k,0)、最高点( 2k,1)下降点(2k,0)最低点(3 2k,1)
数的解析 2 2
式 即得统一的形式:y=Asin(ωx+φ)+B
三角函数图像化简思路:
二次化一次(2倍角、降幂公式),一次再统一(辅助角、两角和差) 即化成统一的形式:y=Asin(ωx+φ)+B
正弦型函数y=Asin(ωx+φ) (A 0) 方法:整体代入
2
⑴ 周期:T
π
12、 ⑵ 奇偶性:当φ=kπ+ 时,y=Asin(ωx+φ)=±Acosωx偶函数;当φ=kπ时,y=Asin(ωx+φ)=±sinωx奇函数
2
正弦型函 ⑶ 最值:当ωx+φ= π
2
+2kπ时,y最大;ωx+φ= +2kπ时,y最小。
数的性质 2
3
⑷ 单调性:增区间: 2kx 2k 减区间: 2kx 2k
2 2 2 2
π
⑸ 对称轴:ωx+φ=kπ+ ;对称中心:ωx+φ=kπ
2
⑴ 三角形内角和定理:ABCC(AB)
①sin C=sin(A+B); ②cos C=-cos(A+B); ③tan C=-tan (A+B);
⑵ 三边关系: 两边之和大于第三边 a+b>c ;两边之差小于第三边 a−b0时,λa与a的方向相同;
算
②当λ<0时,λa与a的方向相反;
③当λ=0时,λa=0
共线向量定理
⑴ 若向量a与b共线,则b=λa.(λ唯一)
3、共线向 → 1 → →
⑵ 若P为线段AB的中点,O为平面内任一点,则OP= (OA+OB)
2
量定理、定
比分点 ⑶ O → A=λO → B+μO → C,A,B,C三点共线 ⇔ λ+μ=1.
定比分点:若AP PB,则
0P
1
0A
0B
1 1
平面向量基本定理:a=λe+λe. 不共线的向量e,e 叫做平面内的一组基底,λ,λ 唯一.
1 1 2 2 1 2 1 2
⑴ 原点(0,0)点A(x , y),则OA (x, y)终点减起点,模 OA x2 y2 .
⑵ 点A(x 1 , y 1 ),点B(x 2 , y 2 ),则AB (x 2 x 1 , y 2 y 1 )终点减起点, AB (x 2 x 1 )2 (y 2 y 1 )2
4、坐标运
算 ⑶ OA (x, y),为实数,则OA (x,y)
⑷ ax,y ,bx ,y ,则ab x x ,y y ,a b (x x , y y )
1 1 2 2 1 2 1 2 1 2 1 2
x x y y
⑸ 点A(x , y),点B(x , y )的中点坐标为( 1 2 ,1 2 )
1 1 2 2 2 2
→ →
⑴向量的夹角:OA=a,OB=b,则∠AOB就是向量a与b的夹角,夹角范围[0,π].
a·b
5、数量积 ⑵数量积定义:a·b=|a||b|·cos θ 夹角公式cos θ= 锐角⇔a·b>0;钝角⇔a·b<0
|a||b|
公式
⑶投影:|a|cos θ叫做向量a在b方向上的投影,|b|cos θ叫做向量b在a方向上的投影
⑷a⊥b⇔a·b=0. a·a=|a|2 |a·b|≤|a||b|.
第 19 页 共 22 页吾日三省吾身:看得懂、记得住、用得了.
⑸当a与b同向,a·b=|a||b|;当a与b反向,a·b=-|a||b|
⑹设向量a=(x,y),b=(x,y),则向量的数量积a·b=xx+yy,
1 1 2 2 1 2 1 2
a·b xx+yy
向量垂直:a⊥b ⇔ xx+yy=0. 向量平行: a∥b⇔ x y=x y cos θ= = 1 2 1 2
1 2 1 2 1 2 2 1 |a||b| x2+y2 x2+y2
1 1 2 2
⑺平面向量数量积运算的常用公式:①(a+b)·(a-b)=a2-b2. ②)(a+b)2=a2+2a·b+b2. ③(a-b)2=a2-2a·b+b2.
(1) 复数的定义:形如z=a+bi的数叫做复数,其中a为实部,b为虚部(i为虚数单位).
(2) 规定:i2 1
(3) 𝔦的幂的周期性:周期T=4
𝖎𝟎=𝟏,𝖎𝟏=𝖎, 𝖎𝟐=−𝟏, 𝖎𝟑=−𝖎 ,𝖎𝟒=𝟏 , 𝔦5=𝔦 …
(4)复数的分类:
实数:b 0,z a bi a
6、复数 复数
虚数:b 0,z a bi 纯虚数a 0,z bi
(5)复数相等:a+bi=c+di ⇔ a=c且b=d
(6)共轭复数:z=a+bi的共轭复数为z abi ,且zz (abi)(abi) a2 b2i2 a2 b2
(7)复数的模:复数z=a+bi的模,|z|=|a+bi|= a2+b2.
(8)在复平面的象限:复数z=a+bi与点(a,b)的象限相同.
第 20 页 共 22 页吾日三省吾身:看得懂、记得住、用得了.
第八部分:排列组合、二项式、期望方程
1.加法原理:做一件事有n类办法,则方法数N=m +m +……+m
1、计数原 1 2 n
理 2.乘法原理:做一件事分n步完成,则方法数N=m m …m
1 2 n
排列定义:n中取m,m排一排(有顺序)
n!
⑴ .排列公式:Am=n(n-1)(n-2)…(n-m+1)= ⑵ 全排列 An nn1n2 21n!
n n-m! n
注意:0! 1,A0 1,A1 n
n n
2、排列组
组合定义:n中取m(无顺序)
合
Am nn-1n-2…n-m+1 n!
⑴ 公式:Cm n = A n m = m! = m!n-m! 注意:C n 0 1,C n n 1,C n 1 n
m
⑵ 组合的性质:① Cm =Cnm ;若Ca Cb,则a b或ab n
n n n n
②
Cm +Cm1 =Cm
(头取大,底加1).
n n n1
⑴ 二项展开式共n1项:abn C0an C1an1bC2an2b2 Cranrbr Cnbn
n n n n n
⑵ 展开式中的通项公式: T Cranrbr (第r1项)
r1 n
⑶ 二项式系数:C0,C1, ,Cn , 二项式系数之和:C0C1 Cr Cn 2n;
n n n n n n n
偶(奇)数项的二项式系数之和相等,即C0C2C4 C1C3C5 2n1
n n n n n n
⑷ 中间项的二项式系数最大. 当两项的系数均为1时,各项的系数等于二项式系数。
当n是偶数时,中间项仅有一项为 ;当n是奇数时,中间项有两项T 和T .
T n-1 n1
n 2 1 2 1 2 1
3、二项式 ⑸ 各项的系数:是指未知数前面的系数。(axb)n a a xa xa xn1 a xn
0 1 2 n1 n
赋值法:① 令x0;a (a b)n
0
② 令x1;a a a a (ab)n (各项的系数之和)
0 1 2 n
③ 令x 1;a a a a a (ab)n
0 1 2 3 n
1
由①③得a a a (②+③)
0 2 4 2
1
a a a (②-③)
1 3 5 2
第 21 页 共 22 页吾日三省吾身:看得懂、记得住、用得了.
1.离散型随机变量的均值与方差
随机变量常用字母X,Y,ξ,η,…表示
步骤:第一步列表;第二步代公式
变量X x x … x … x
1 2 i n
概率P p p … p … p
1 2 i n
分布列的性质①: p i0,(i=1,2,3…n) ②: p
1
+p
2
+p
3
+…+p
n
=1.
(1)期望:E(X)=x p +x p +…+xp+…+x p
1 1 2 2 i i n n
(2)方差: DX n x EX2p
i i
i1
期望方差的性质:
(1)E(aX+b)=aE(X)+b
(2)D(aX+b)=a2D(X)
(3)D (𝒙)=E(𝒙𝟐)-[𝑬(𝒙)]𝟐
2.常见的离散型随机变量的分布列
(1)两点分布: X 0 1
P 1-p p
4、
其中p=P(X=1)称为成功概率.若随机变量X服从两点分布,则E(X)=p,D(X)=p(1-p)
期望
(2)超几何分布:在含有M 个特殊元素的N 个元素中,不放回的任取n件,其中含有特殊元素的个数记为X ,
方差
CkCnk
则有PX k M NM ,k 0,1,2, ,m,即:
Cn
N
X 0 1 m
C0Cn0 C1Cn1 CmCnm
P M NM M NM M NM
Cn Cn Cn
N N N
(3)二项分布:在n次独立重复试验中,事件A发生的概率为 p,设在n次试验中事件A发生的次数为随机变量
X,则有PX kCkpk1 pnk,k 0,1,2, n ,即:
n
X 0 1 k n
P C01 pn C1p1pn1 Ckpk1 pnk Cnpn
n n n n
若随机变量X服从二项分布X~B(n,p),则E(X)=np,D(X)=np(1-p).
第 22 页 共 22 页