文档内容
专题 1.2 空间向量的数量积运算【五大题型】
【人教A版(2019)】
【题型1 空间向量数量积的计算】..........................................................................................................................2
【题型2 空间向量的夹角及其应用】......................................................................................................................2
【题型3 利用空间向量的数量积求模】..................................................................................................................3
【题型4 向量垂直的应用】......................................................................................................................................4
【题型5 投影向量的求解】......................................................................................................................................5
【知识点1 空间向量的夹角与数量积】
1.空间向量的夹角
(1)定义:已知两个非零向量a,b,在空间任取一点O,作OA=a,OB=b,则∠AOB叫做向量a,b
的夹角,记作〈a,b〉.
(2)范围:0≤〈a,b〉≤π.
特别地,当〈a,b〉=时,a⊥b.
2.空间向量的数量积
已知两个非零向量a,b,则|a||b|cos 〈a,b〉叫做a,b的数量积,记作
a·b.
定义
即a·b=|a||b|cos〈a,b〉.
规定:零向量与任何向量的数量积都为0.
①a⊥b a·b=0
性质
②a·a=a2=|a|2
⇔
①(λa)·b=λ(a·b),λ∈R.
运算律 ②a·b=b·a(交换律).
③a·(b+c)=a·b+a·c(分配律).
3.空间向量夹角的计算
求两个向量的夹角:利用公式 = 求 ,进而确定 .
学科网(北京)股份有限公司4.空间向量数量积的计算
求空间向量数量积的步骤:
(1)将各向量分解成已知模和夹角的向量的组合形式.
(2)利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积.
(3)代入 求解.
【题型1 空间向量数量积的计算】
【例1】(2023秋·高一单元测试)在空间四边形ABCD中,⃗AB·⃗CD+⃗AC·⃗DB+⃗AD·⃗BC等于( )
A.−1 B.0 C.1 D.不确定
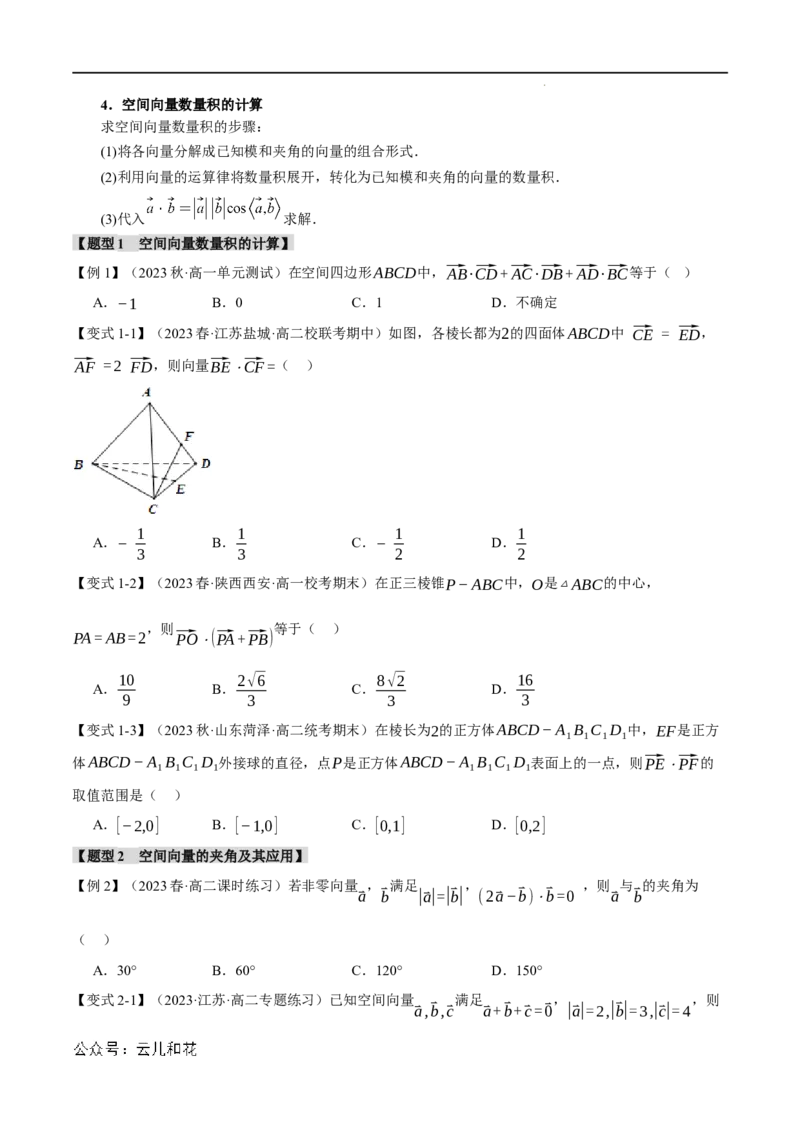
【变式1-1】(2023春·江苏盐城·高二校联考期中)如图,各棱长都为2的四面体ABCD中 ⃗CE = ⃗ED,
⃗AF =2 ⃗FD,则向量⃗BE⋅⃗CF=( )
1 1 1 1
A.− B. C.− D.
3 3 2 2
【变式1-2】(2023春·陕西西安·高一校考期末)在正三棱锥P−ABC中,O是△ABC的中心,
,则 等于( )
PA=AB=2 ⃗PO⋅(⃗PA+⃗PB)
10 2√6 8√2 16
A. B. C. D.
9 3 3 3
【变式1-3】(2023秋·山东菏泽·高二统考期末)在棱长为2的正方体ABCD−A B C D 中,EF是正方
1 1 1 1
体ABCD−A B C D 外接球的直径,点P是正方体ABCD−A B C D 表面上的一点,则⃗PE⋅⃗PF的
1 1 1 1 1 1 1 1
取值范围是( )
A.[−2,0] B.[−1,0] C.[0,1] D.[0,2]
【题型2 空间向量的夹角及其应用】
【例2】(2023春·高二课时练习)若非零向量 , 满足 , ,则 与 的夹角为
⃑a ⃑b |⃑a|=|⃑b| (2⃑a−⃑b)⋅⃑b=0 ⃑a ⃑b
( )
A.30° B.60° C.120° D.150°
【变式2-1】(2023·江苏·高二专题练习)已知空间向量 满足 , ,则
⃑a,⃑b,⃑c ⃑a+⃑b+⃑c=0⃑ |⃑a|=2,|⃑b|=3,|⃑c|=4
学科网(北京)股份有限公司⃑a与⃑b的夹角为( )
A.30° B.45°
C.60° D.以上都不对
π
【变式2-2】(2023春·高二课时练习)空间四边形OABC中,OB=OC,∠AOB=∠AOC= ,则
3
cos⟨⃑OA,⃑BC⟩的值是( )
1 √2 1
A. B. C.− D.0
2 2 2
【变式2-3】(2023春·高二课时练习)已知⃑e ,⃑e 是夹角为60°的两个单位向量,则⃑a=⃑e +⃑e 与
1 2 1 2
的夹角为( )
⃑b=⃑e −2⃑e
1 2
A.60° B.120°
C.30° D.90°
【题型3 利用空间向量的数量积求模】
【例3】(2023春·福建宁德·高二校联考期中)已知单位向量 , , 中, , ,
⃗a ⃗b ⃗c ⃗a⊥⃗b ⟨⃗a,⃗c⟩=⟨⃗b,⃗c⟩=60°
则 ( )
|⃗a−⃗b+2⃗c|=
A.√5 B.5 C.6 D.√6
【变式3-1】(2023·江苏·高二专题练习)已知在平行六面体ABCD−A B C D 中,向量⃗AB,⃗AD,
1 1 1 1
两两的夹角均为 ,且 , , ,则 ( )
⃗A A 60° |⃗AB|=1 |⃗AD|=2 |⃗A A |=3 |⃗AC |=
1 1 1
A.5 B.6 C.4 D.8
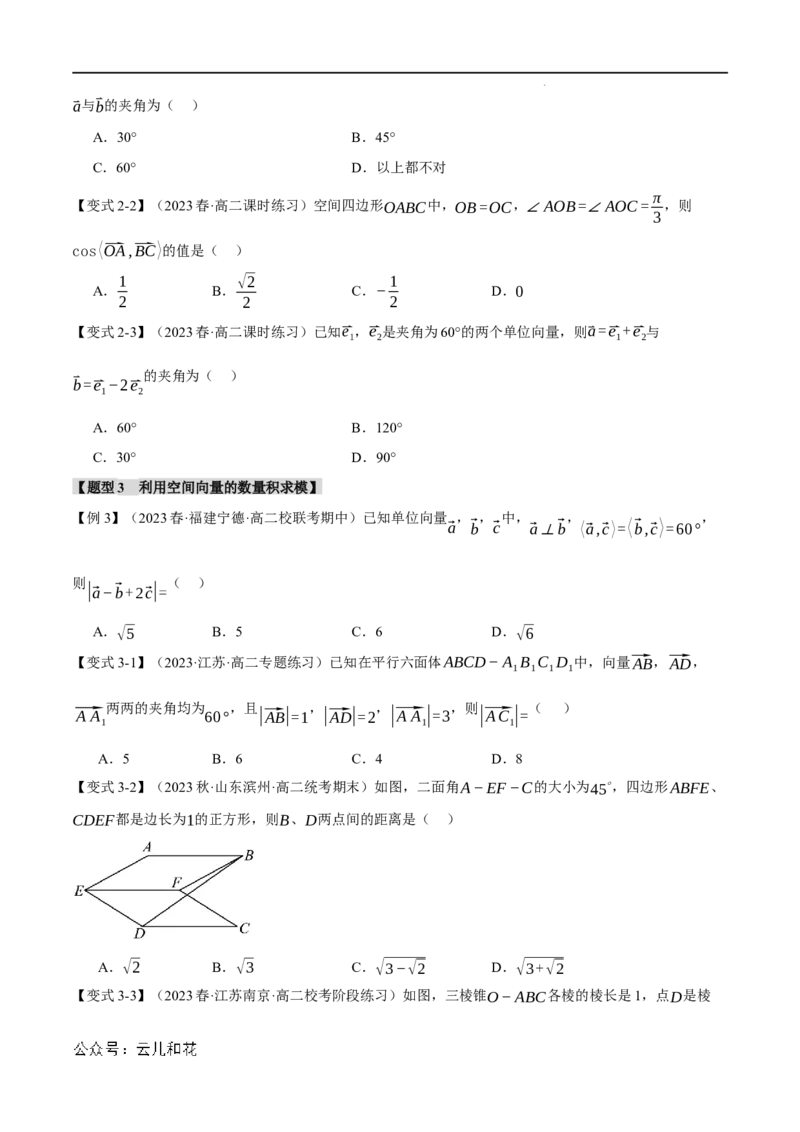
【变式3-2】(2023秋·山东滨州·高二统考期末)如图,二面角A−EF−C的大小为45∘,四边形ABFE、
CDEF都是边长为1的正方形,则B、D两点间的距离是( )
A.√2 B.√3 C.√3−√2 D.√3+√2
【变式3-3】(2023春·江苏南京·高二校考阶段练习)如图,三棱锥O−ABC各棱的棱长是1,点D是棱
学科网(北京)股份有限公司AB的中点,点E在棱OC上,且⃗OE=λ⃗OC,则DE的最小值为( )
1 √2 √3
A. B. C. D.1
2 2 2
【题型4 向量垂直的应用】
【例4】(2023春·甘肃武威·高二统考期中)在空间,已知⃗e ,⃗e 为单位向量,且⃗e ⊥⃗e ,若⃗a=2⃗e +3⃗e ,
1 2 1 2 1 2
⃗a=k⃗e −4⃗e ,⃗a⊥⃗b,则实数k的值为( )
1 2
A.-6 B.6
C.3 D.-3
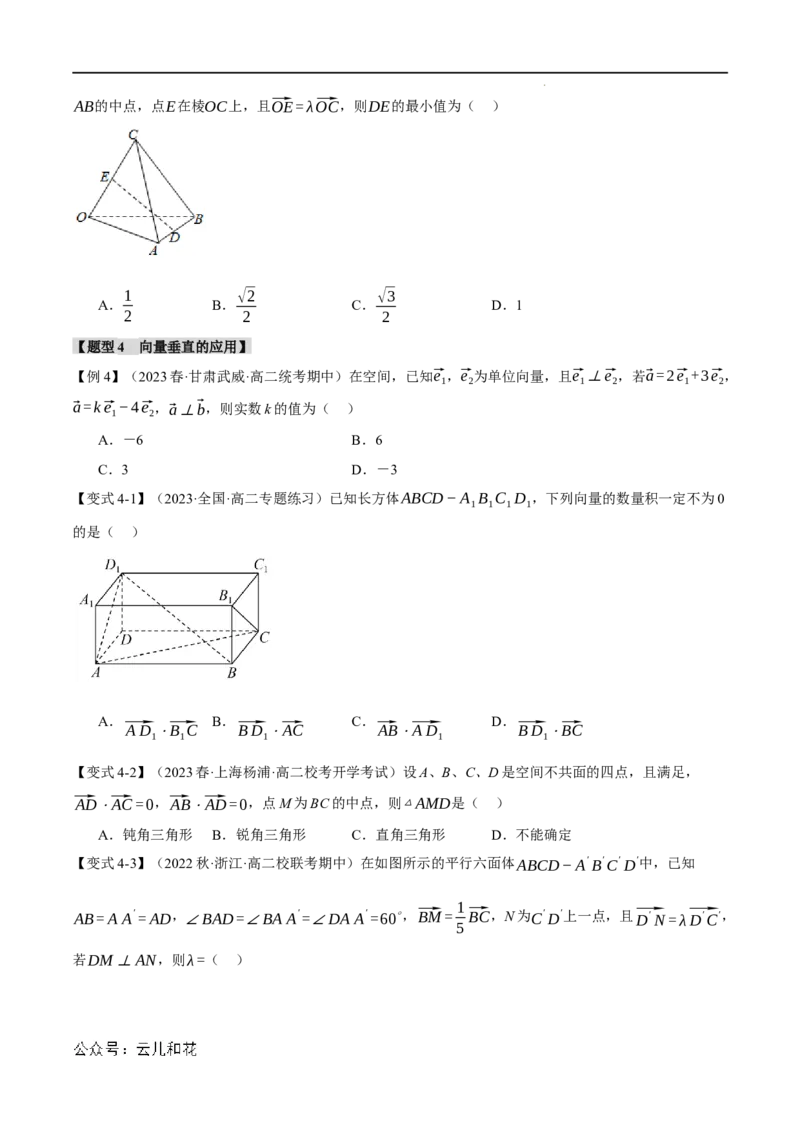
【变式4-1】(2023·全国·高二专题练习)已知长方体ABCD−A B C D ,下列向量的数量积一定不为0
1 1 1 1
的是( )
A. B. C. D.
⃗AD ⋅⃗B C ⃗BD ⋅⃗AC ⃗AB⋅⃗AD ⃗BD ⋅⃗BC
1 1 1 1 1
【变式4-2】(2023春·上海杨浦·高二校考开学考试)设A、B、C、D是空间不共面的四点,且满足,
⃗AD⋅⃗AC=0,⃗AB⋅⃗AD=0,点M为BC的中点,则△AMD是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.不能确定
【变式4-3】(2022秋·浙江·高二校联考期中)在如图所示的平行六面体ABCD−A′B′C′D′中,已知
1
AB=A A′=AD,∠BAD=∠BA A′=∠DA A′=60∘,⃗BM= ⃗BC,N为C′D′上一点,且⃗ D′N=λ ⃗ D′C′,
5
若DM⊥AN,则λ=( )
学科网(北京)股份有限公司1 1 1 1
A. B. C. D.
2 3 4 5
【知识点2 向量的投影】
1.向量 的投影
(1)如图(1),在空间,向量a向向量b投影,由于它们是自由向量,因此可以先将它们平移到同一个平
面α内,进而利用平面上向量的投影,得到与向量b共线的向量c,c=|a|cos〈a,b〉,向量c称为向量a
在向量b上的投影向量.类似地,可以将向量a向直线l投影(如图(2)).
(2)如图(3),向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为
A′,B′,得到A′B′,向量A′B′称为向量a在平面β上的投影向量.这时,向量a,A′B′的夹角就是向量a
所在直线与平面β所成的角.
【题型5 投影向量的求解】
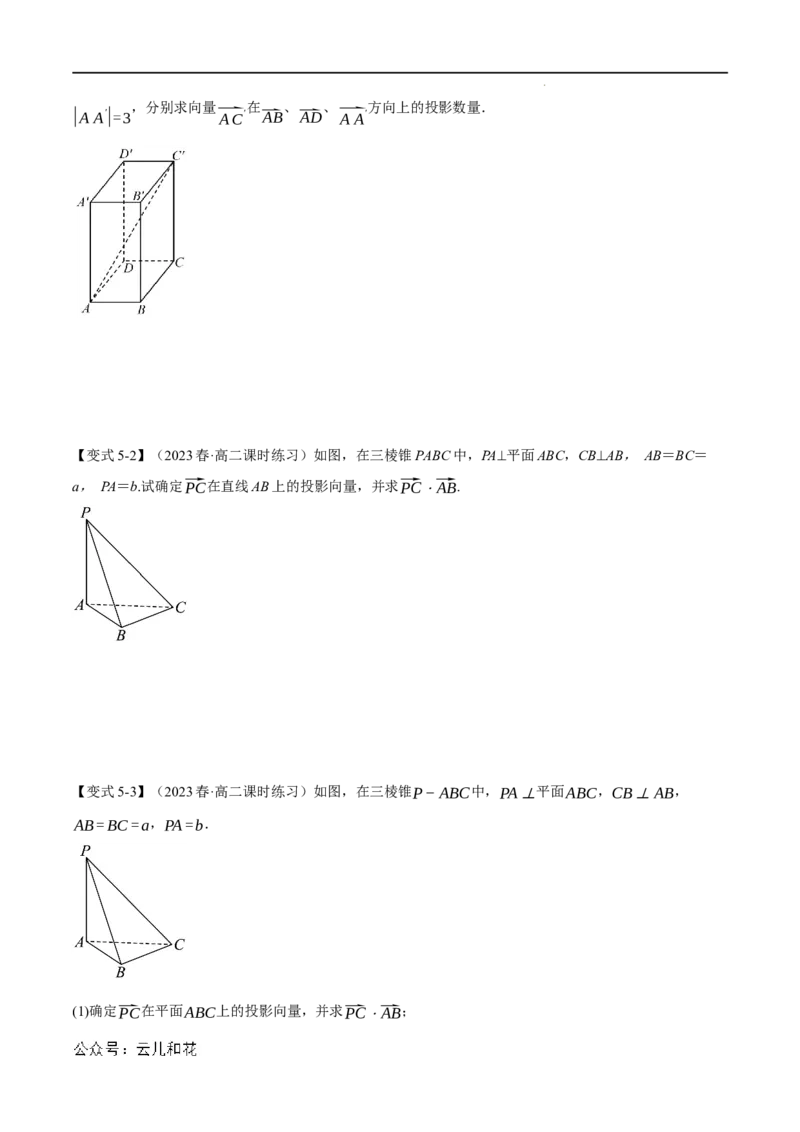
【例5】(2023春·高二课时练习)如图,在三棱锥P−ABC中,PA⊥平面ABC,CB⊥AB,
AB=BC=a,PA=b.试确定⃗PC在⃗AB上的投影向量,并求⃗PC⋅⃗AB.
【变式5-1】(2022·全国·高三专题练习)如图,在长方体ABCD−A′B′C′D′中,已知|AB|=1,|AD|=2,
学科网(北京)股份有限公司,分别求向量 在 、 、 方向上的投影数量.
|A A′|=3 ⃑AC′ ⃑AB ⃑AD ⃑A A′
【变式5-2】(2023春·高二课时练习)如图,在三棱锥PABC中,PA⊥平面ABC,CB⊥AB, AB=BC=
a, PA=b.试确定⃗PC在直线AB上的投影向量,并求⃗PC⋅⃗AB.
【变式5-3】(2023春·高二课时练习)如图,在三棱锥P−ABC中,PA⊥平面ABC,CB⊥AB,
AB=BC=a,PA=b.
(1)确定⃑PC在平面ABC上的投影向量,并求⃑PC⋅⃑AB;
学科网(北京)股份有限公司(2)确定⃑PC在⃑AB上的投影向量,并求⃑PC⋅⃑AB.
学科网(北京)股份有限公司