文档内容
专题 1.3 空间向量基本定理【八大题型】
【人教A版(2019)】
【题型1 空间向量基底的判断】..............................................................................................................................1
【题型2 用空间基底表示向量】..............................................................................................................................2
【题型3 由空间向量基本定理求参数】..................................................................................................................3
【题型4 正交分解】..................................................................................................................................................4
【题型5 利用空间向量基本定理证明平行、共线、共面问题】.........................................................................5
【题型6 利用空间向量基本定理求夹角】..............................................................................................................7
【题型7 利用空间向量基本定理证明垂直问题】.................................................................................................9
【题型8 利用空间向量基本定理求距离(长度)问题】.........................................................................................10
【知识点1 空间向量基本定理】
1.空间向量基本定理
如果三个向量a,b,c不共面,那么对任意一个空间向量p,存在唯一的有序实数组(x,y,z),使得p
=xa+yb+zc.
我们把{a,b,c}叫做空间的一个基底,a,b,c都叫做基向量.
2.用基底表示向量的步骤:
(1)定基底:根据已知条件,确定三个不共面的向量构成空间的一个基底.
(2)找目标:用确定的基底(或已知基底)表示目标向量,需要根据三角形法则及平行四边形法则,结
合
相等向量的代换、向量的运算进行变形、化简,最后求出结果.
(3)下结论:利用空间的一个基底{ , , }可以表示出空间所有向量.表示要彻底,结果中只能含
有 , , ,不能含有其他形式的向量.
【题型1 空间向量基底的判断】
【例1】(2023春·河南开封·高二统考期末)若 构成空间的一个基底,则下列向量可以构成空间基
{⃗a,⃗b,⃗c}
底的是( )
学科网(北京)股份有限公司A.⃗a+⃗b,⃗a−⃗b,⃗a B.⃗a+⃗b,⃗a−⃗b,⃗b C.⃗a+⃗b,⃗a−⃗b,⃗b+⃗c D.⃗a+⃗b,⃗a+⃗b+⃗c,⃗c
【变式1-1】(2023春·湖南·高一校联考期末)已知 是空间的一个基底,若 , ,则
{⃗a,⃗b,⃗c} ⃗p=⃗a+⃗b ⃗q=⃗a+⃗c
下列与⃗p,⃗q构成一组空间基底的是( )
A.r⃗=2⃗b−3⃗c B.r⃗=⃗a−⃗b+2⃗c
C.r⃗=⃗a+2⃗b−⃗c D.r⃗=2⃗a+⃗b+⃗c
【变式1-2】(2023春·内蒙古兴安盟·高二校考阶段练习)若⃗a,⃗b,⃗c构成空间的一个基底,则下列向量
能构成空间的一个基底的是( )
A.⃗a+⃗b,⃗a−⃗c,⃗b B.⃗c,⃗b+⃗c,⃗b−⃗c
C.⃗b+⃗c,⃗a+⃗b+⃗c,⃗a D.⃗a,⃗a+⃗b,⃗a−⃗b
【变式1-3】(2023秋·云南大理·高二统考期末)若 是空间的一个基底,且向量
{⃗e ,⃗e ,⃗e }
1 2 3
不能构成空间的一个基底,则 ( )
{⃗OA=⃗e +⃗e +⃗e ,⃗OB=⃗e −2⃗e +2⃗e ,⃗OC=⃗ke +3⃗e +⃗2e } k=
1 2 3 1 2 3 1 2 3
8 5 1 9
A. B. C.− D.
3 2 4 4
【题型2 用空间基底表示向量】
【例2】(2023·全国·高二专题练习)在四面体O−ABC中,⃗PA=2⃗OP,Q是BC的中点,且M为PQ的
中点,若⃗OA=⃗a,⃗OB=⃗b,⃗OC=⃗c,则⃗OM=( )
1 1 1 1 1 1
A. ⃗a+ ⃗b+ ⃗c B. ⃗a+ ⃗b+ ⃗c
6 4 4 6 2 2
1 1 1 1 1 1
C. ⃗a+ ⃗b+ ⃗c D. ⃗a+ ⃗b+ ⃗c
3 2 2 3 4 4
【变式2-1】(2023春·福建龙岩·高二校联考期中)如图,在直三棱柱ABC−A B C 中,E为棱A C 的
1 1 1 1 1
中点.设 , , ,则 ( )
⃗BA=⃗a ⃗BB =⃗b ⃗BC=⃗c ⃗BE=
1
学科网(北京)股份有限公司1 1 1 1
A. ⃗a+⃗b+ ⃗c B. ⃗a+ ⃗b+⃗c
2 2 2 2
1 1 1
C.⃗a+ ⃗b+ ⃗c D. ⃗a+⃗b+⃗c
2 2 2
1
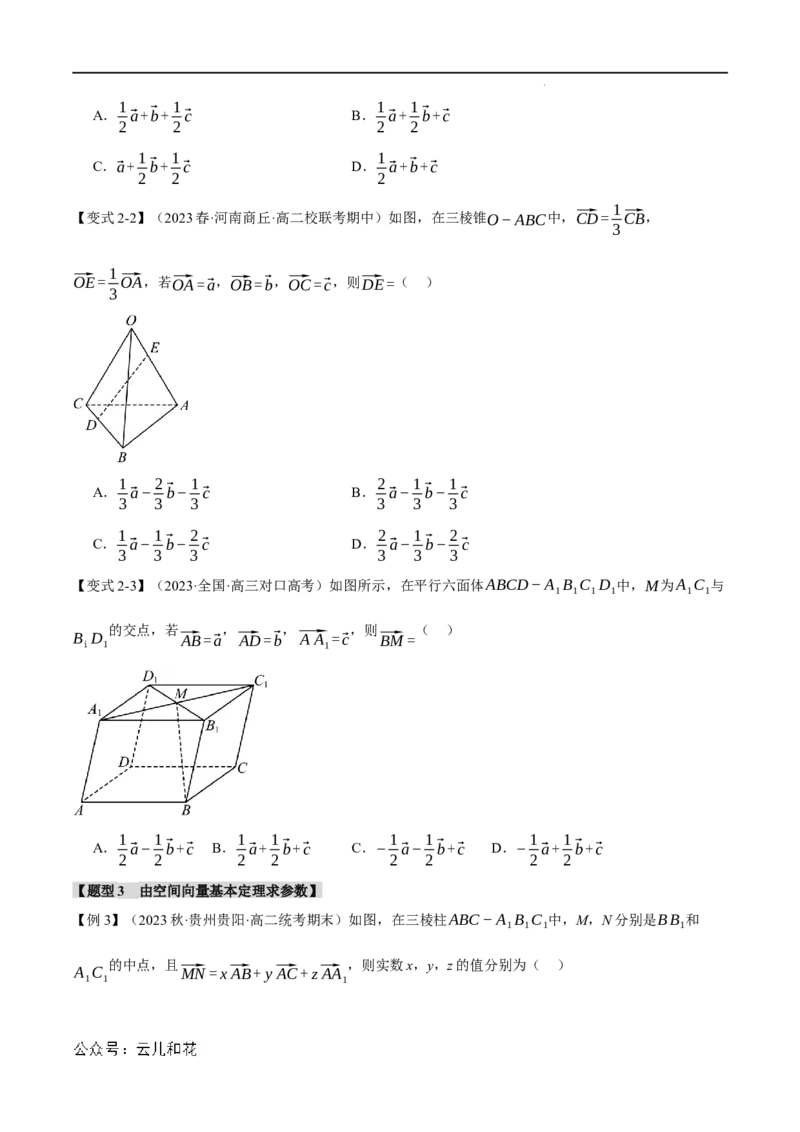
【变式2-2】(2023春·河南商丘·高二校联考期中)如图,在三棱锥O−ABC中,⃗CD= ⃗CB,
3
1
⃗OE= ⃗OA,若⃗OA=⃗a,⃗OB=⃗b,⃗OC=⃗c,则⃗DE=( )
3
1 2 1 2 1 1
A. ⃗a− ⃗b− ⃗c B. ⃗a− ⃗b− ⃗c
3 3 3 3 3 3
1 1 2 2 1 2
C. ⃗a− ⃗b− ⃗c D. ⃗a− ⃗b− ⃗c
3 3 3 3 3 3
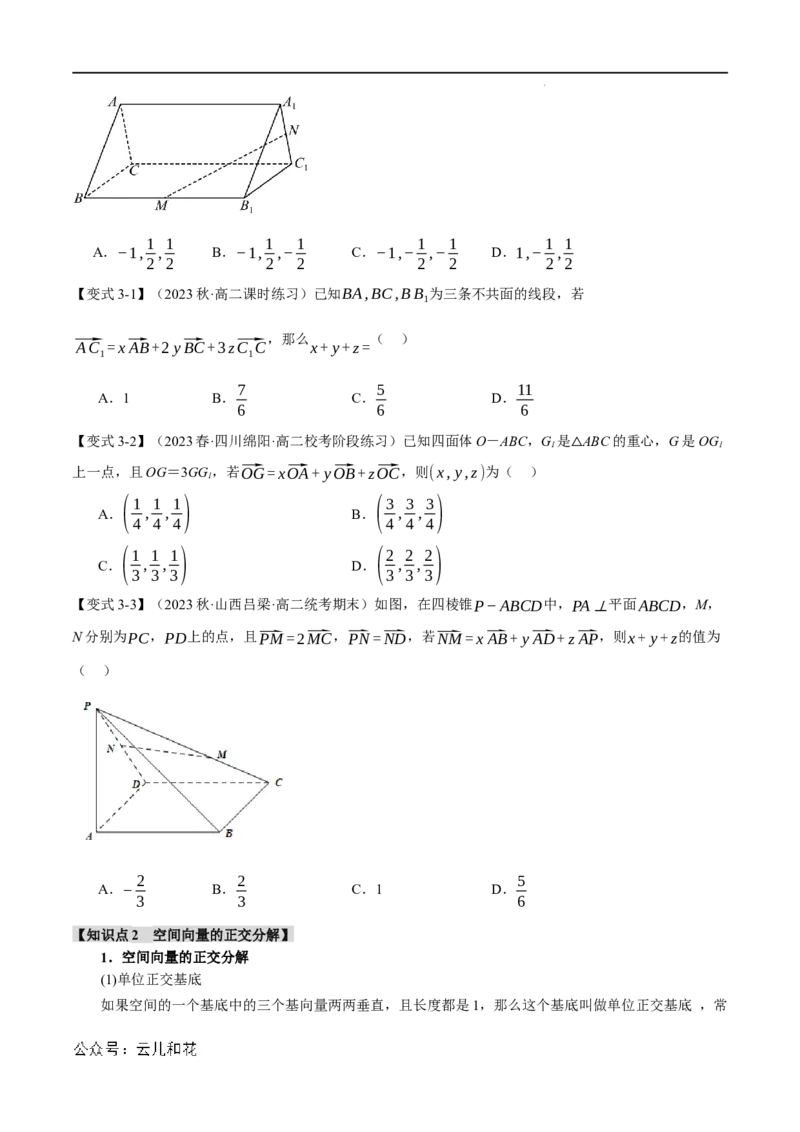
【变式2-3】(2023·全国·高三对口高考)如图所示,在平行六面体ABCD−A B C D 中,M为A C 与
1 1 1 1 1 1
的交点,若 , , ,则 ( )
B D ⃗AB=⃗a ⃗AD=⃗b ⃗A A =⃗c ⃗BM=
i 1 1
1 1 1 1 1 1 1 1
A. ⃗a− ⃗b+⃗c B. ⃗a+ ⃗b+⃗c C.− ⃗a− ⃗b+⃗c D.− ⃗a+ ⃗b+⃗c
2 2 2 2 2 2 2 2
【题型3 由空间向量基本定理求参数】
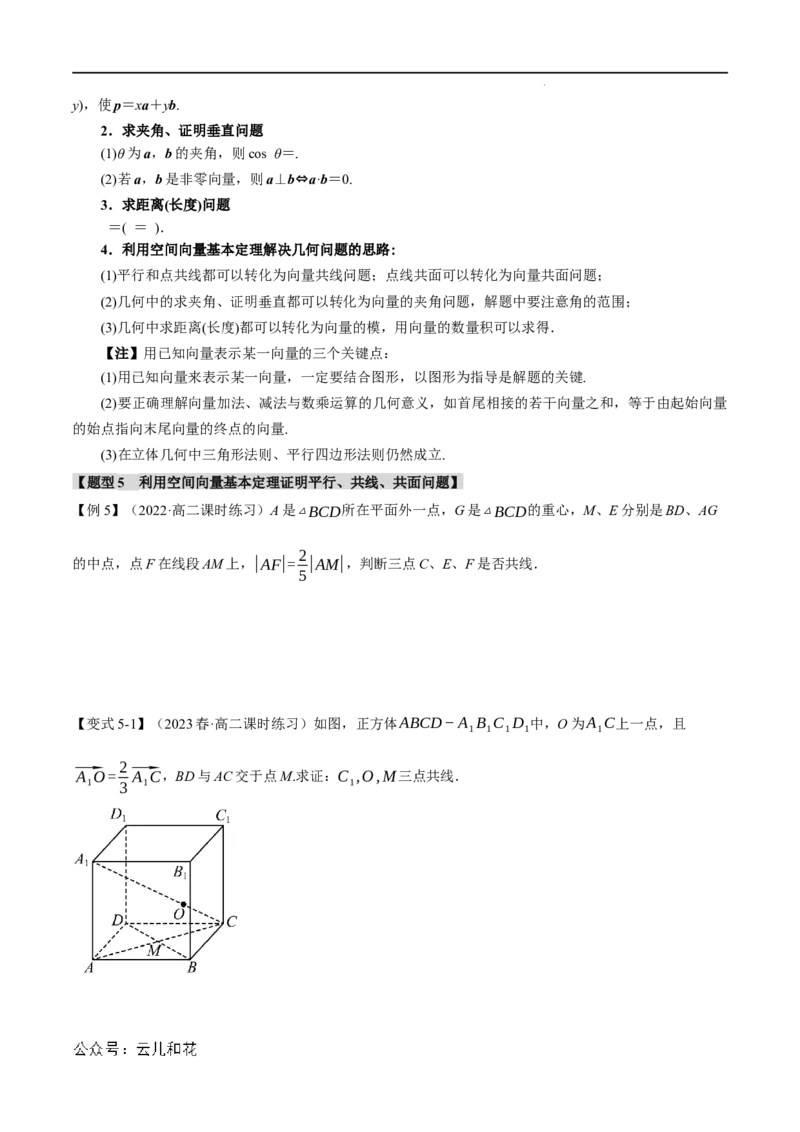
【例3】(2023秋·贵州贵阳·高二统考期末)如图,在三棱柱ABC−A B C 中,M,N分别是BB 和
1 1 1 1
的中点,且 ,则实数x,y,z的值分别为( )
A C ⃗MN=x⃗AB+ y⃗AC+z⃗AA
1 1 1
学科网(北京)股份有限公司1 1 1 1 1 1 1 1
A.−1, , B.−1, ,− C.−1,− ,− D.1,− ,
2 2 2 2 2 2 2 2
【变式3-1】(2023秋·高二课时练习)已知BA,BC,BB 为三条不共面的线段,若
1
,那么 ( )
⃗AC =x⃗AB+2y⃗BC+3z⃗C C x+ y+z=
1 1
7 5 11
A.1 B. C. D.
6 6 6
【变式3-2】(2023春·四川绵阳·高二校考阶段练习)已知四面体O-ABC,G 是 ABC的重心,G是OG
1 1
上一点,且OG=3GG ,若⃗OG=x⃗OA+ y⃗OB+z⃗OC,则(x,y,z)为( ) △
1
(1 1 1) (3 3 3)
A. , , B. , ,
4 4 4 4 4 4
(1 1 1) (2 2 2)
C. , , D. , ,
3 3 3 3 3 3
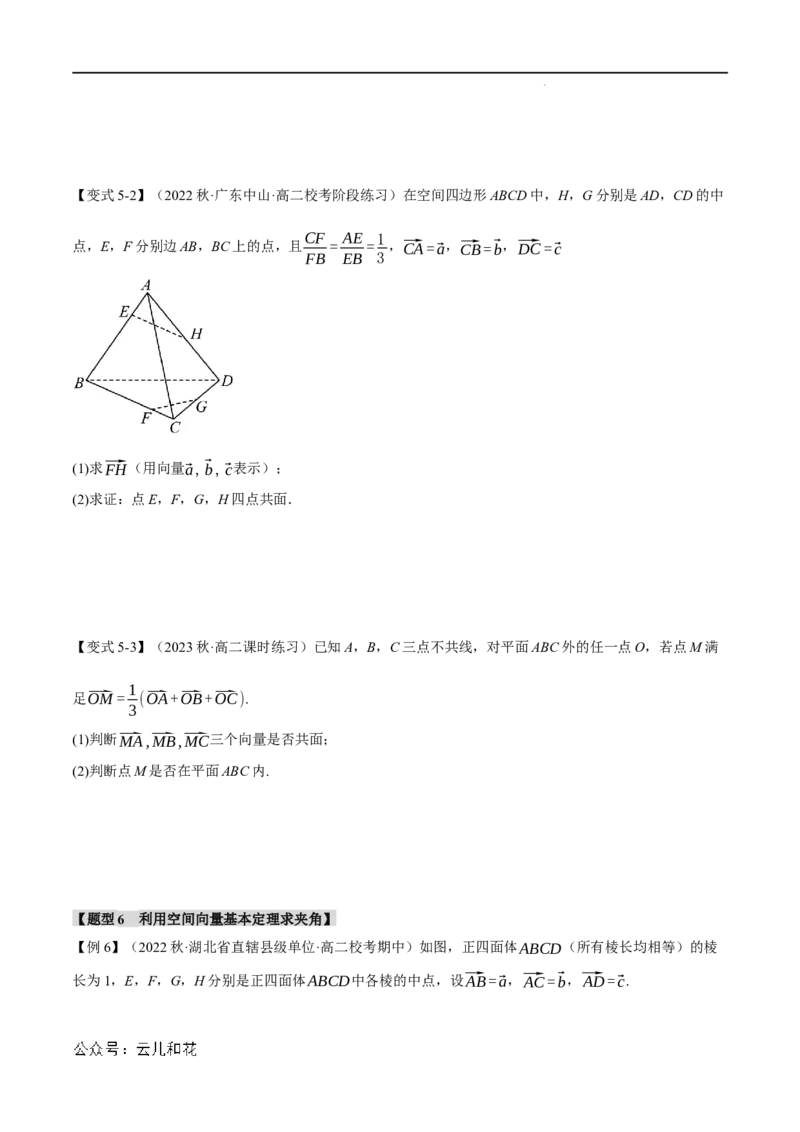
【变式3-3】(2023秋·山西吕梁·高二统考期末)如图,在四棱锥P−ABCD中,PA⊥平面ABCD,M,
N分别为PC,PD上的点,且⃑PM=2⃑MC,⃑PN=⃑ND,若⃑NM=x⃑AB+ y⃑AD+z⃑AP,则x+ y+z的值为
( )
2 2 5
A.− B. C.1 D.
3 3 6
【知识点2 空间向量的正交分解】
1.空间向量的正交分解
(1)单位正交基底
如果空间的一个基底中的三个基向量两两垂直,且长度都是1,那么这个基底叫做单位正交基底 ,常
学科网(北京)股份有限公司用{i,j,k}表示.
(2)向量的正交分解
由空间向量基本定理可知,对空间任一向量a,均可以分解为三个向量xi,yj,zk使得a=xi+yj+zk.
像这样把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
【题型4 正交分解】
【例4】(2022·全国·高一假期作业)设 是单位正交基底,已知向量 在基底 下的坐标为
{i⃗,⃗j,⃗k} ⃗p {⃗a,⃗b,⃗c}
,其中 , , ,则向量 在基底 下的坐标是( )
(8,6,4) ⃗a=i⃗+⃗j ⃗b=⃗j+⃗k ⃗c=⃗k+i⃗ ⃗p {i⃗,⃗j,⃗k}
A.(10,12,14) B.(12,14,10) C.(14,12,10) D.(4,3,2)
【变式4-1】(2023春·高二课时练习)已知 是空间的一个单位正交基底,向量 ,
{⃗a,⃗b,⃗c} ⃗p=⃗a+2⃗b+3⃗c
是空间的另一个基底,向量 在基底 下的坐标为( )
{⃗a+⃗b,⃗a−⃗b,⃗c} ⃗p {⃗a+⃗b,⃗a−⃗b,⃗c}
(3 1 ) ( 3 1 ) (1 3 ) ( 1 3 )
A. ,− ,3 B. − , ,3 C. ,− ,3 D. − , ,3
2 2 2 2 2 2 2 2
【变式4-2】(2023秋·河北邯郸·高二统考期末)已知SA⊥平面ABC,AB⊥AC,SA=AB=1,
BC=√5,则空间的一个单位正交基底可以为( )
{ 1 }
A. ⃗AB, ⃗AC,⃗AS B.{⃗AB,⃗AC,⃗AS}
2
C.{ 1 1 } D.{ √5 }
⃗AB, ⃗AC, ⃗AS ⃗AS,⃗AB, ⃗BC
2 2 5
【变式4-3】(2022秋·山西大同·高二校考阶段练习)已知向量⃗a,⃗b,⃗c是空间的一个单位正交基底,向量
⃗a+⃗b,⃗a−⃗b,⃗a+⃗c是空间的另一个基底,若向量⃗p在基底⃗a,⃗b,⃗c下的坐标为(2,3,4),则⃗p在⃗a+⃗b,⃗a−⃗b,
⃗a+⃗c下的坐标为( )
( 1 5 ) (5 1 )
A. − , ,4 B. , ,4
2 2 2 2
(1 5 ) (5 1 )
C. ,− ,4 D. ,− ,4
2 2 2 2
【知识点3 用空间向量基本定理解决相关的几何问题】
1.证明平行、共线、共面问题
(1)对于空间任意两个向量a,b(b≠0),a∥b的充要条件是存在实数λ,使a=λb.
(2)如果两个向量a,b不共线,那么向量p与向量a,b共面的充要条件是存在唯一的有序实数对(x,
学科网(北京)股份有限公司y),使p=xa+yb.
2.求夹角、证明垂直问题
(1)θ为a,b的夹角,则cos θ=.
(2)若a,b是非零向量,则a⊥b⇔a·b=0.
3.求距离(长度)问题
=( = ).
4.利用空间向量基本定理解决几何问题的思路:
(1)平行和点共线都可以转化为向量共线问题;点线共面可以转化为向量共面问题;
(2)几何中的求夹角、证明垂直都可以转化为向量的夹角问题,解题中要注意角的范围;
(3)几何中求距离(长度)都可以转化为向量的模,用向量的数量积可以求得.
【注】用已知向量表示某一向量的三个关键点:
(1)用已知向量来表示某一向量,一定要结合图形,以图形为指导是解题的关键.
(2)要正确理解向量加法、减法与数乘运算的几何意义,如首尾相接的若干向量之和,等于由起始向量
的始点指向末尾向量的终点的向量.
(3)在立体几何中三角形法则、平行四边形法则仍然成立.
【题型5 利用空间向量基本定理证明平行、共线、共面问题】
【例5】(2022·高二课时练习)A是△BCD所在平面外一点,G是△BCD的重心,M、E分别是BD、AG
2
的中点,点F在线段AM上,|AF|= |AM|,判断三点C、E、F是否共线.
5
【变式5-1】(2023春·高二课时练习)如图,正方体ABCD−A B C D 中,O为A C上一点,且
1 1 1 1 1
2
⃗A O= ⃗A C,BD与AC交于点M.求证:C ,O,M三点共线.
1 3 1 1
学科网(北京)股份有限公司【变式5-2】(2022秋·广东中山·高二校考阶段练习)在空间四边形ABCD中,H,G分别是AD,CD的中
CF AE 1
点,E,F分别边AB,BC上的点,且 = = ,⃗CA=⃗a,⃗CB=⃗b,⃗DC=⃗c
FB EB 3
(1)求⃗FH(用向量⃗a,⃗b,⃗c表示);
(2)求证:点E,F,G,H四点共面.
【变式5-3】(2023秋·高二课时练习)已知A,B,C三点不共线,对平面ABC外的任一点O,若点M满
1
足⃑OM= (⃑OA+⃑OB+⃑OC).
3
(1)判断⃑MA,⃑MB,⃑MC三个向量是否共面;
(2)判断点M是否在平面ABC内.
【题型6 利用空间向量基本定理求夹角】
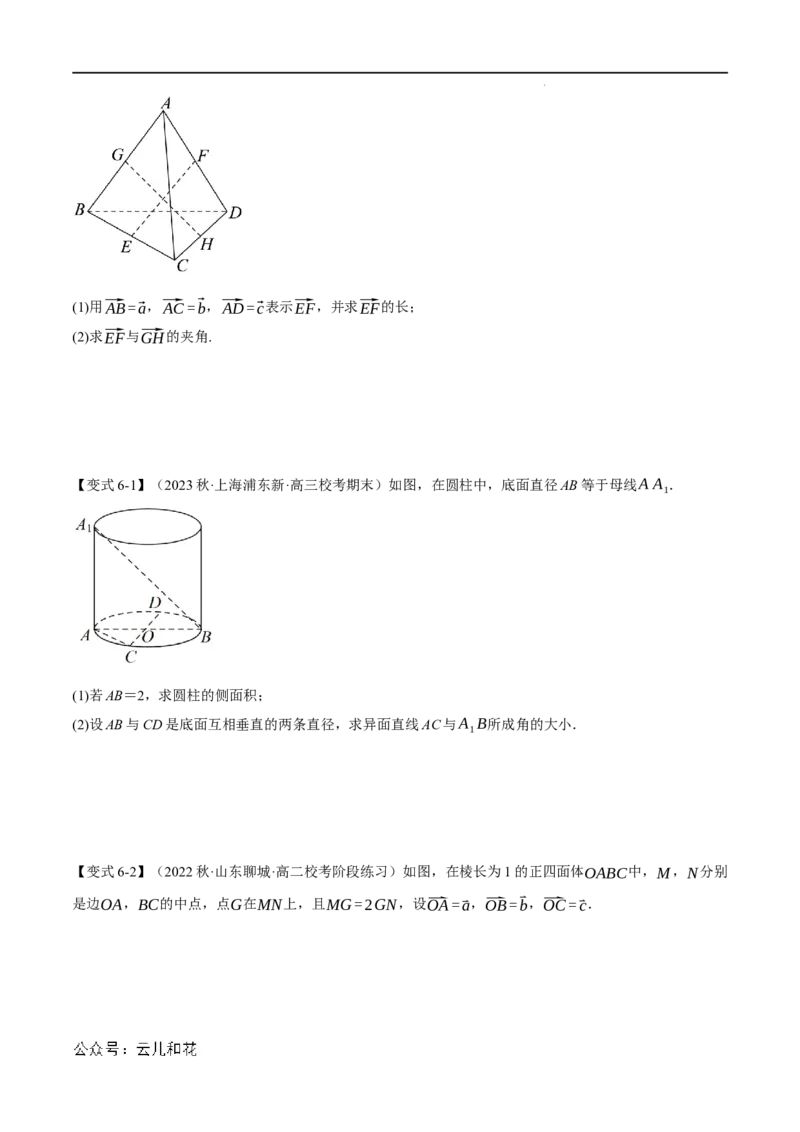
【例6】(2022秋·湖北省直辖县级单位·高二校考期中)如图,正四面体ABCD(所有棱长均相等)的棱
长为1,E,F,G,H分别是正四面体ABCD中各棱的中点,设⃗AB=⃗a,⃗AC=⃗b,⃗AD=⃗c.
学科网(北京)股份有限公司(1)用⃗AB=⃗a,⃗AC=⃗b,⃗AD=⃗c表示⃗EF,并求⃗EF的长;
(2)求⃗EF与⃗GH的夹角.
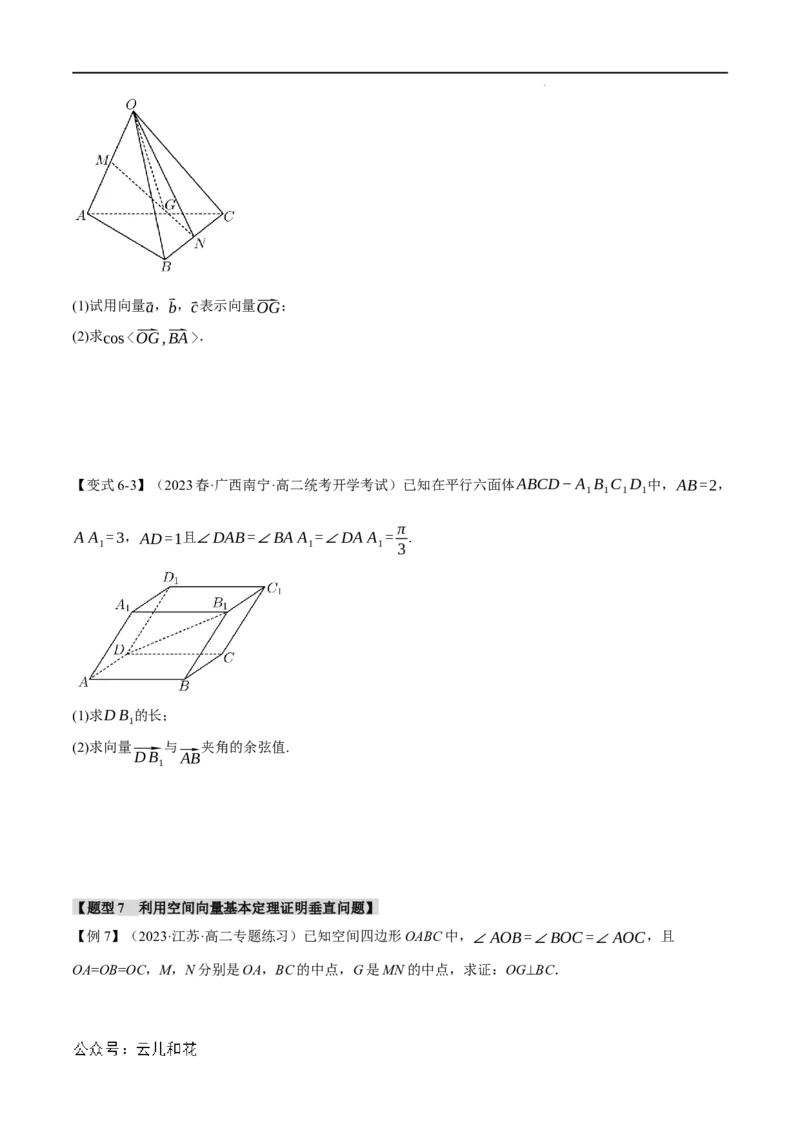
【变式6-1】(2023秋·上海浦东新·高三校考期末)如图,在圆柱中,底面直径AB等于母线A A .
1
(1)若AB=2,求圆柱的侧面积;
(2)设AB与CD是底面互相垂直的两条直径,求异面直线AC与A B所成角的大小.
1
【变式6-2】(2022秋·山东聊城·高二校考阶段练习)如图,在棱长为1的正四面体OABC中,M,N分别
是边OA,BC的中点,点G在MN上,且MG=2GN,设⃑OA=⃑a,⃑OB=⃑b,⃑OC=⃑c.
学科网(北京)股份有限公司(1)试用向量⃑a,⃑b,⃑c表示向量⃑OG;
(2)求cos<⃑OG,⃑BA>.
【变式6-3】(2023春·广西南宁·高二统考开学考试)已知在平行六面体ABCD−A B C D 中,AB=2,
1 1 1 1
π
A A =3,AD=1且∠DAB=∠BA A =∠DA A = .
1 1 1 3
(1)求DB 的长;
1
(2)求向量 与 夹角的余弦值.
⃗DB ⃗AB
1
【题型7 利用空间向量基本定理证明垂直问题】
【例7】(2023·江苏·高二专题练习)已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且
OA=OB=OC,M,N分别是OA,BC的中点,G是MN的中点,求证:OG⊥BC.
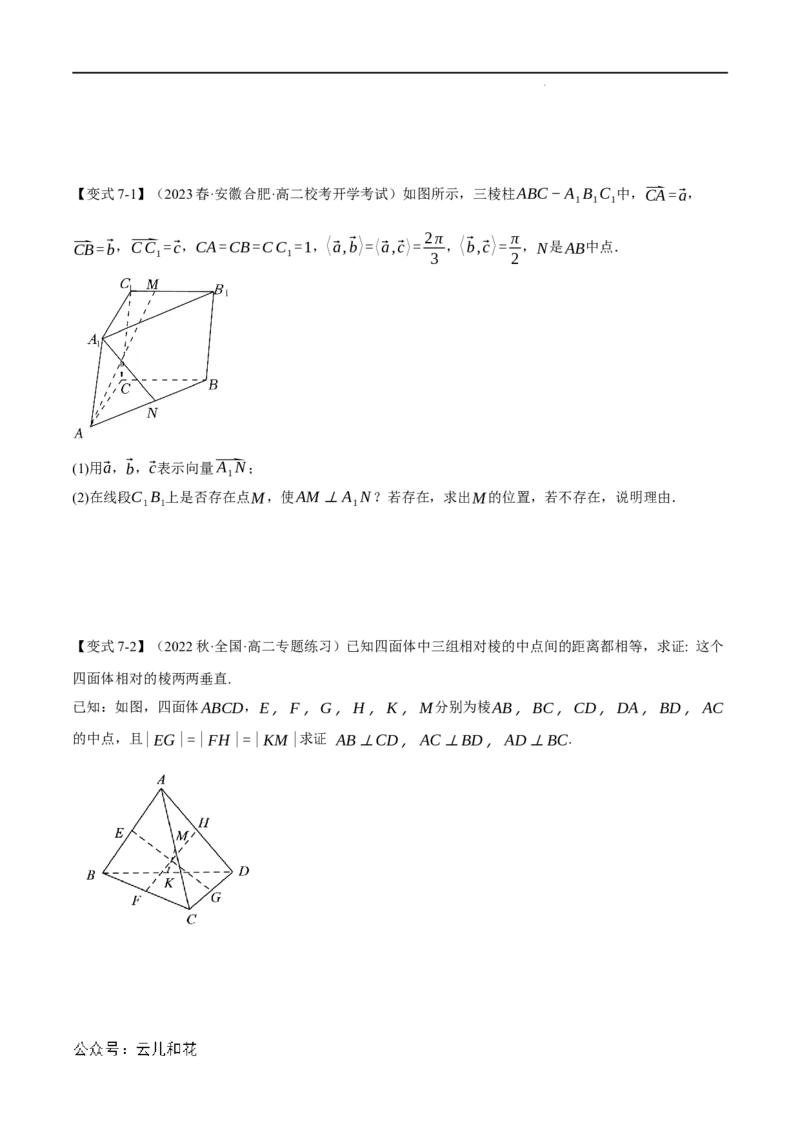
学科网(北京)股份有限公司【变式7-1】(2023春·安徽合肥·高二校考开学考试)如图所示,三棱柱ABC−A B C 中,⃑CA=⃗a,
1 1 1
2π π
⃑CB=⃗b,⃑CC =⃗c,CA=CB=CC =1,⟨⃗a,⃗b⟩=⟨⃗a,⃗c⟩= ,⟨⃗b,⃗c⟩= ,N是AB中点.
1 1 3 2
(1)用⃗a,⃗b,⃗c表示向量⃑A N;
1
(2)在线段C B 上是否存在点M,使AM⊥A N?若存在,求出M的位置,若不存在,说明理由.
1 1 1
【变式7-2】(2022秋·全国·高二专题练习)已知四面体中三组相对棱的中点间的距离都相等,求证: 这个
四面体相对的棱两两垂直.
已知:如图,四面体ABCD,E,F,G,H,K,M分别为棱AB,BC,CD,DA,BD,AC
的中点,且|EG|=|FH|=|KM|求证 AB⊥CD,AC⊥BD,AD⊥BC.
学科网(北京)股份有限公司【变式7-3】(2022秋·北京顺义·高二校考阶段练习)如图,在底面ABCD为菱形的平行六面体
1 1
ABCD−A B C D 中,M,N分别在棱A A ,CC 上,且A M= A A ,CN= CC ,且
1 1 1 1 1 1 1 3 1 3 1
.
∠A AD=∠A AB=∠DAB=60∘
1 1
(1)用向量 表示向量 ;
⃗A A ,⃗AD,⃗AB ⃗MN
1
(2)求证:D,M,B ,N共面;
1
A A
(3)当 1为何值时,AC ⊥A B.
AB 1 1
【题型8 利用空间向量基本定理求距离(长度)问题】
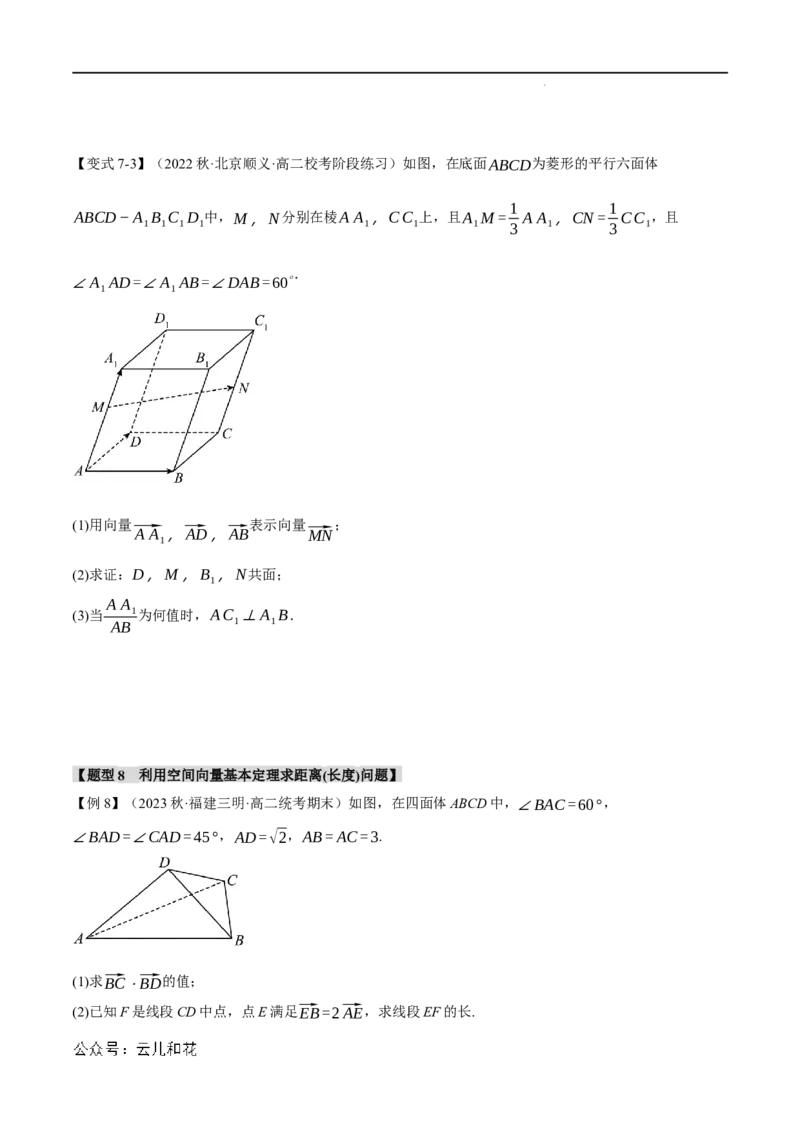
【例8】(2023秋·福建三明·高二统考期末)如图,在四面体ABCD中,∠BAC=60°,
∠BAD=∠CAD=45°,AD=√2,AB=AC=3.
(1)求⃗BC⋅⃗BD的值;
(2)已知F是线段CD中点,点E满足⃗EB=2⃗AE,求线段EF的长.
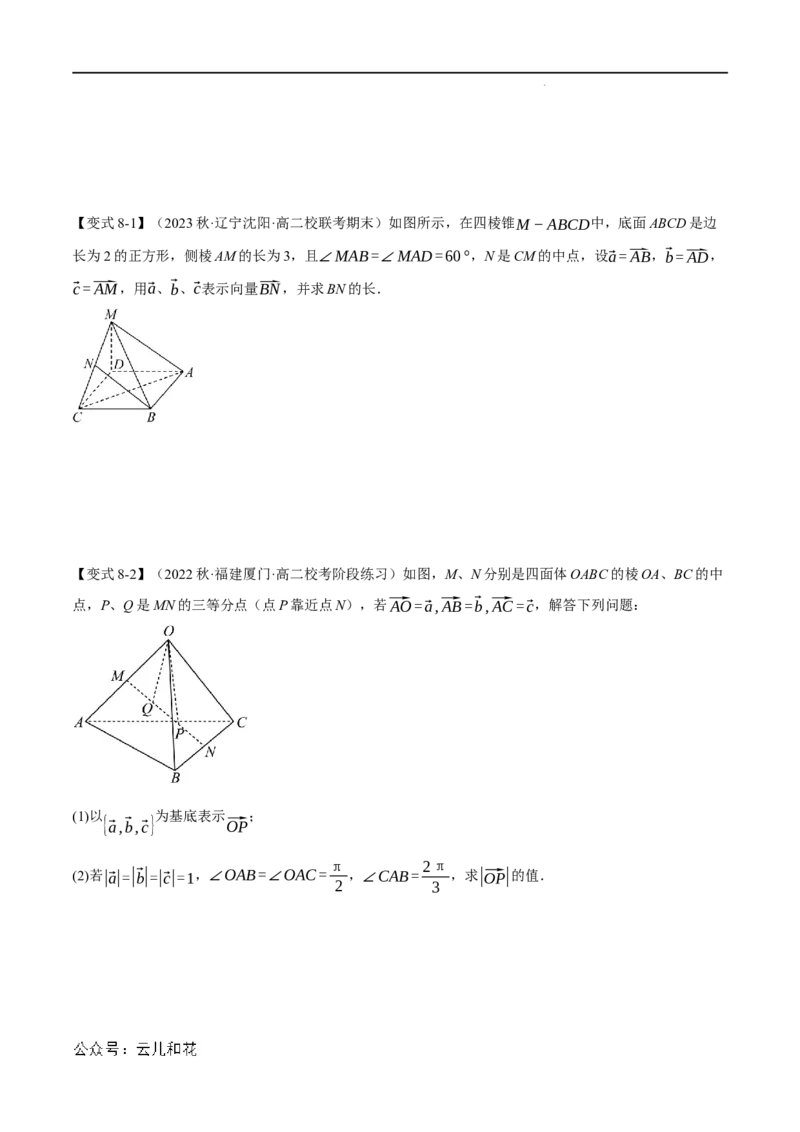
学科网(北京)股份有限公司【变式8-1】(2023秋·辽宁沈阳·高二校联考期末)如图所示,在四棱锥M−ABCD中,底面ABCD是边
长为2的正方形,侧棱AM的长为3,且∠MAB=∠MAD=60°,N是CM的中点,设⃗a=⃑AB,⃗b=⃑AD,
⃗c=⃑AM,用⃗a、⃗b、⃗c表示向量⃑BN,并求BN的长.
【变式8-2】(2022秋·福建厦门·高二校考阶段练习)如图,M、N分别是四面体OABC的棱OA、BC的中
点,P、Q是MN的三等分点(点P靠近点N),若⃗AO=⃗a,⃗AB=⃗b,⃗AC=⃗c,解答下列问题:
(1)以 为基底表示 ;
{⃗a,⃗b,⃗c} ⃗OP
π 2π
(2)若|⃗a|=|⃗b|=|⃗c|=1,∠OAB=∠OAC= ,∠CAB= ,求|⃗OP|的值.
2 3
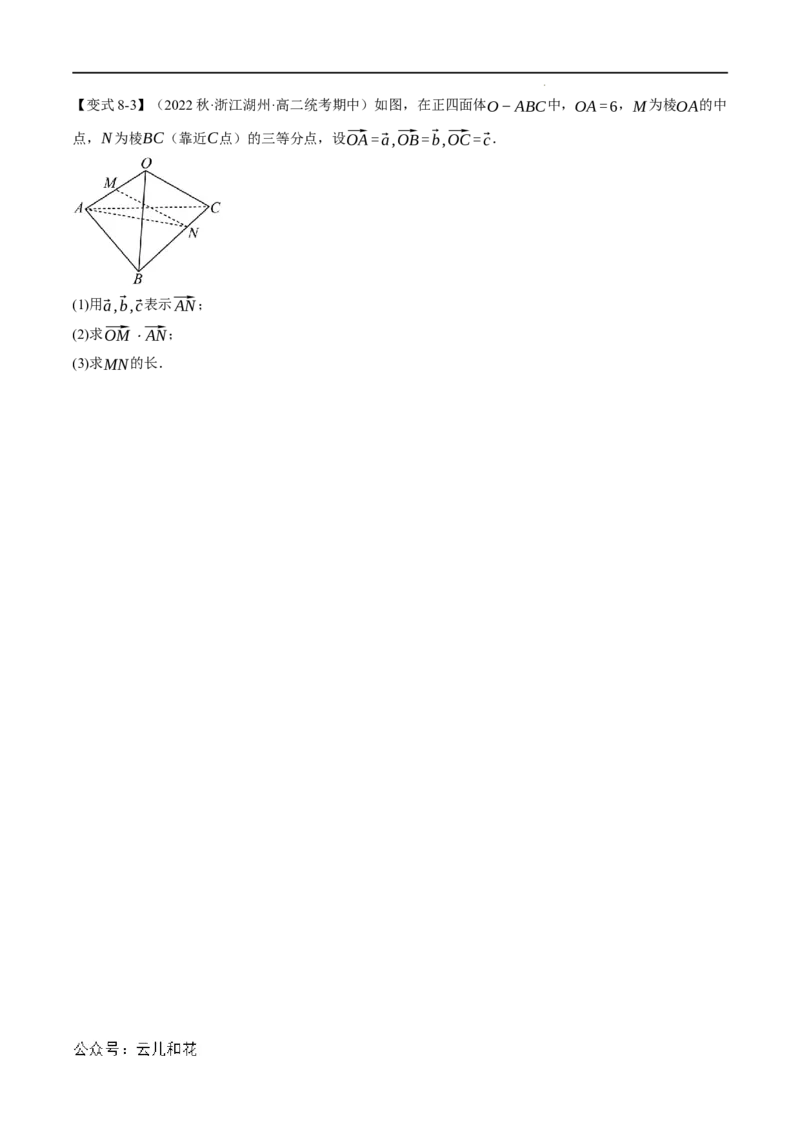
学科网(北京)股份有限公司【变式8-3】(2022秋·浙江湖州·高二统考期中)如图,在正四面体O−ABC中,OA=6,M为棱OA的中
点,N为棱BC(靠近C点)的三等分点,设⃗OA=⃗a,⃗OB=⃗b,⃗OC=⃗c.
(1)用⃗a,⃗b,⃗c表示⃗AN;
(2)求⃗OM⋅⃗AN;
(3)求MN的长.
学科网(北京)股份有限公司