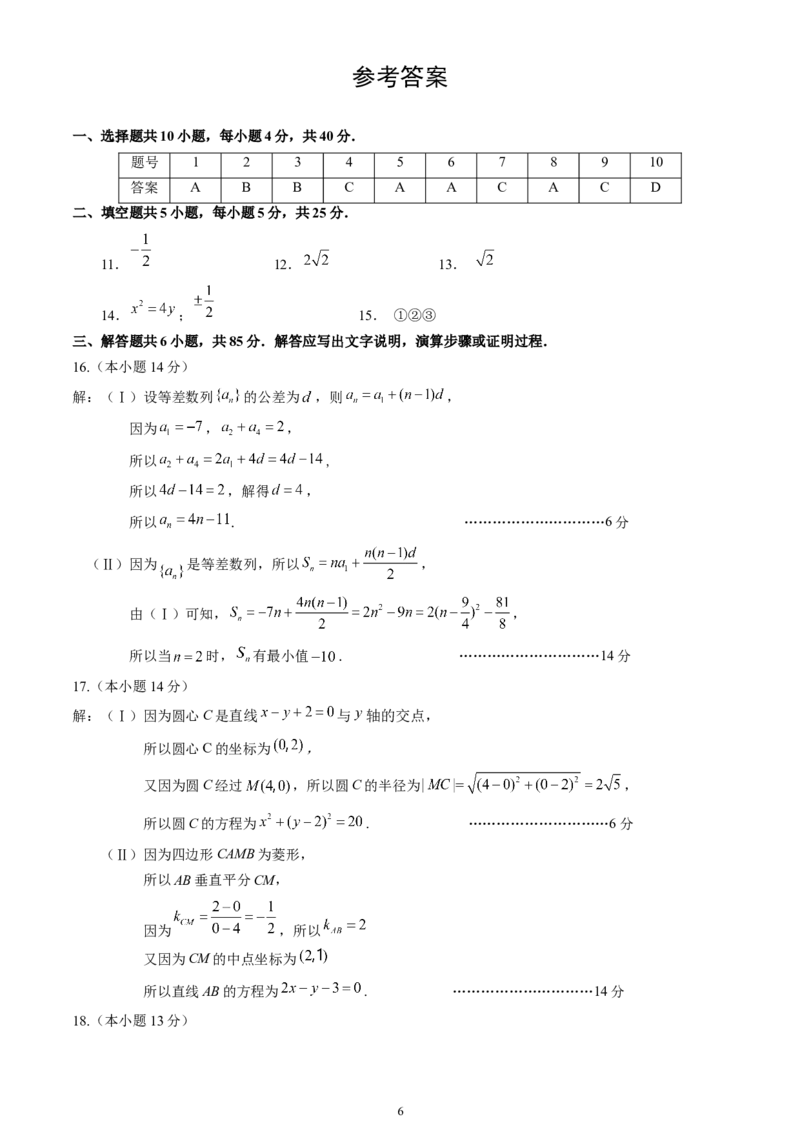文档内容
北京市丰台区 2024-2025 学年高二上学期期末考试
数 学
2025.01
1. 答题前,考生务必先将答题卡上的学校、班级、姓名、教育ID号用黑色字
迹签字笔填写清楚,并认真核对条形码上的教育ID号、姓名,在答题卡的
“条形码粘贴区”贴好条形码。
考 2. 本次练习所有答题均在答题卡上完成。选择题必须使用 2B铅笔以正确填涂
生 方式将各小题对应选项涂黑,如需改动,用橡皮擦除干净后再选涂其它选
须 项。非选择题必须使用标准黑色字迹签字笔书写,要求字体工整、字迹清
知 楚。
3. 请严格按照答题卡上题号在相应答题区内作答,超出答题区域书写的答案无
效,在练习卷、草稿纸上答题无效。
4. 本练习卷满分共150分,作答时长120分钟。
第一部分 选择题(共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知向量 , ,则
(A) (B) (C) (D)
2.直线 的倾斜角为
(A) (B) (C) (D)
3.与直线 关于x轴对称的直线方程为
(A) (B)
(C) (D)
4.已知圆 与圆 外切,则
(A) (B) (C)7 (D)13
5.已知向量 , ,则向量 在向量 上的投影向量为
(A) (B) (C) ( D )
6.已知圆 及点 ,在圆 上任取一点 ,连接
1,将点 折叠到点A,记 与折痕 的交点为 (如图). 当点 在圆 上运动时,点 的
轨迹方程为
(A) (B)
(C) (D)
7.在空间直角坐标系 中, , , ,D 是平面 ABC 内一点,若
,则 的最小值为
(A) (B) (C) (D)3
8.设椭圆 与双曲线 的离心率分别为 , ,若双曲线渐近线的斜率均
小于 ,则 的取值范围是
(A) (B) (C) (D)
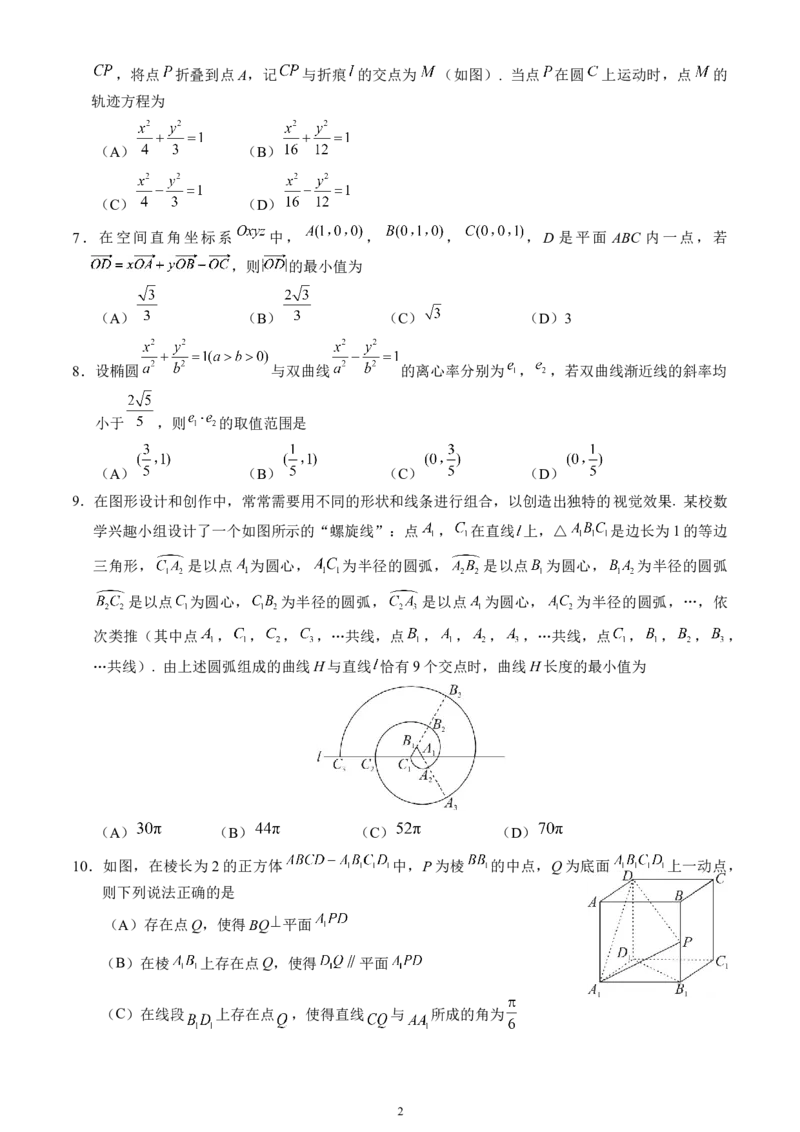
9.在图形设计和创作中,常常需要用不同的形状和线条进行组合,以创造出独特的视觉效果. 某校数
学兴趣小组设计了一个如图所示的“螺旋线”:点 , 在直线 上,△ 是边长为1的等边
三角形, 是以点 为圆心, 为半径的圆弧, 是以点 为圆心, 为半径的圆弧
是以点 为圆心, 为半径的圆弧, 是以点 为圆心, 为半径的圆弧,…,依
次类推(其中点 , , , ,…共线,点 , , , ,…共线,点 , , , ,
…共线). 由上述圆弧组成的曲线H与直线 恰有9个交点时,曲线H长度的最小值为
(A) (B) (C) (D)
10.如图,在棱长为2的正方体 中,P为棱 的中点,Q为底面 上一动点,
则下列说法正确的是
(A)存在点Q,使得BQ 平面
(B)在棱 上存在点Q,使得 平面
(C)在线段 上存在点 ,使得直线 与 所成的角为
2(D)存在点 ,使得三棱锥 的体积为2
第二部分 非选择题(共110分)
二、填空题共5小题,每小题5分,共25分。
11.已知平面a的一个法向量为 ,平面b的一个法向量为 ,若 ,则
_______.
12.直线 : 被圆 : 截得的弦AB的长为 .
13.在棱长为2的正四面体ABCD中,M,N分别是AB,CD的中点,则|MN|= .
14.已知点 ,直线 ,动圆P过点F,且与直线l相切,则圆心P的轨迹C的方程为
_______;若直线 及 分别与曲线C交于异于原点的M,N两点. 当直线MN过点F
时, .
15.已知方程 所表示的曲线为C. 给出以下四个结论:
①曲线C与y轴有两个不同交点;
②曲线C关于原点对称;
③x轴及直线 为曲线C的两条渐近线;
④若曲线C与圆 有公共点,则r的最小值为 .
其中,所有正确结论的序号是________.
三、解答题共6小题,共85分。解答应写出文字说明,演算步骤或证明过程。
16.(本小题14分)
已知数列 是等差数列, ,且 .
(Ⅰ)求 的通项公式;
(Ⅱ)求 的前n项和 的最小值,以及 取得最小值时n的值.
317.(本小题14分)
已知圆C经过点 ,且圆心C是直线 与 轴的交点.
(Ⅰ)求圆C的方程;
(Ⅱ)若直线l与圆C交于A,B两点,且四边形CAMB为菱形,求直线l的方程.
18.(本小题13分)
已知抛物线 的焦点为F,过点F的直线l与C交于A,B两点(其中点A在第一
象限),点A到抛物线C的准线的距离为 .
(Ⅰ)求直线l的斜率;
(Ⅱ)若 ,求 的值.
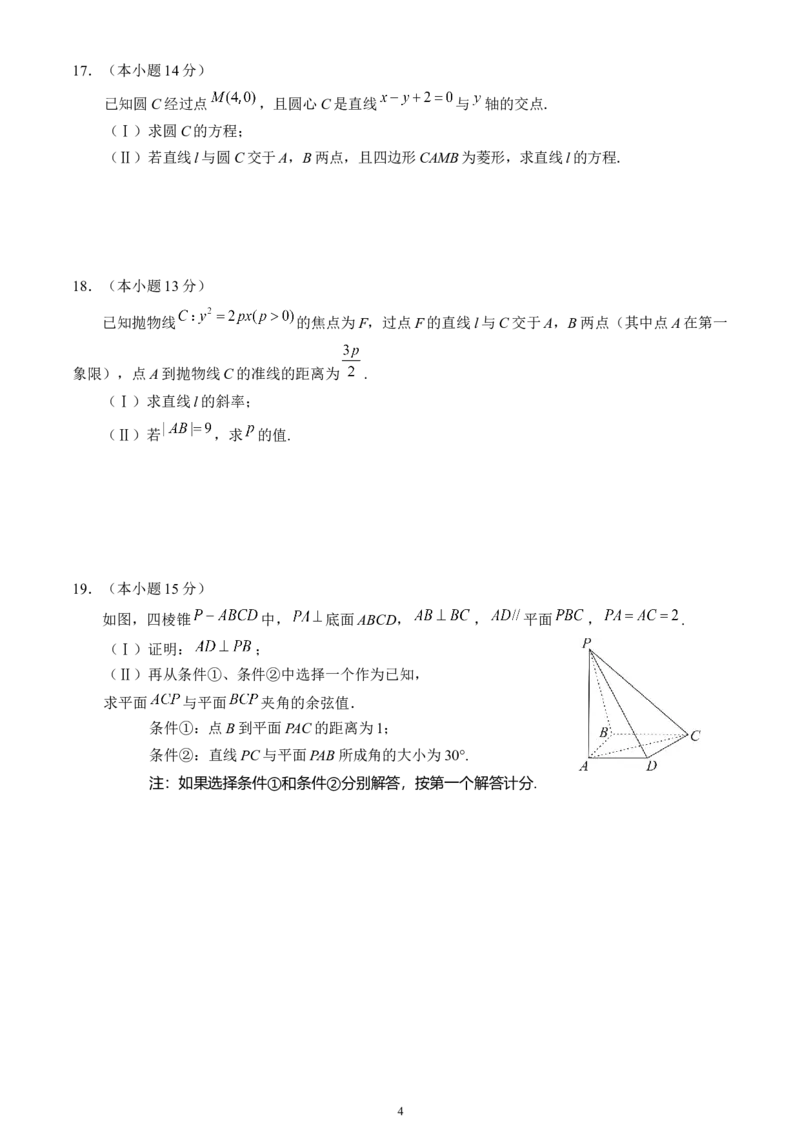
19.(本小题15分)
如图,四棱锥 中, 底面ABCD, , 平面 , .
(Ⅰ)证明: ;
(Ⅱ)再从条件①、条件②中选择一个作为已知,
求平面 与平面 夹角的余弦值.
条件①:点B到平面PAC的距离为1;
条件②:直线PC与平面PAB所成角的大小为30°.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
420.(本小题15分)
已知椭圆 过点 ,长轴长为4.
(Ⅰ)求椭圆E的方程及离心率;
(Ⅱ)若直线l: 与椭圆E交于A,B两点,过点B作斜率为0的直线与椭圆的另一个
交点为D. 求证:直线AD过定点.
21.(本小题共14分)
已知无穷数列 各项均为正数,且 .
(Ⅰ)请判断如下两个结论是否正确:
① ;② ;
(Ⅱ)当 时,证明: ;
(Ⅲ)记数列 的前 项和为 ,若 ,证明: .
(考生务必将答案答在答题卡上,在试卷上作答无效)
5参考答案
一、选择题共10小题,每小题4分,共40分.
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B C A A C A C D
二、填空题共5小题,每小题5分,共25分.
11. 12. 13.
14. ; 15. ①②③
三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.
16.(本小题14分)
解:(Ⅰ)设等差数列 的公差为 ,则 ,
因为 , ,
所以 ,
所以 ,解得 ,
所以 . …………………………6分
(Ⅱ)因为 是等差数列,所以 ,
由(Ⅰ)可知, ,
所以当 时, 有最小值 . …………………………14分
17.(本小题14分)
解:(Ⅰ)因为圆心C是直线 与 轴的交点,
所以圆心C的坐标为 ,
又因为圆C经过 ,所以圆C的半径为 ,
所以圆C的方程为 . …………………………6分
(Ⅱ)因为四边形CAMB为菱形,
所以AB垂直平分CM,
因为 ,所以
又因为CM的中点坐标为
所以直线AB的方程为 . …………………………14分
18.(本小题13分)
6(Ⅰ)设点A的坐标 ,
因为点A到抛物线准线的距离是 ,
所以 ,所以 ,代入抛物线方程得:
所以点 ,又因为点 ,
所以直线l的斜率 . …………………………6分
(Ⅱ)因为抛物线C的焦点F ,所以直线l的方程为:
由 得: ,
可知 恒成立,
设点B的坐标 ,则 ,
,所以 . …………………………13分
19.(本小题15分)
解:(Ⅰ)因为 底面ABCD, 平面ABCD,
所以 , ,
因为 , , 平面PAB,
所以 平面 ,
因为PB⊂平面 ,所以 ,
因为 平面 , 平面ABCD,平面ABCD∩平面PBC=BC,
所以 ,
所以 . …………………………7分
(Ⅱ)由(Ⅰ)可知,PA,AB,AD两两垂直,以A为原点, AB,AD,AP所在直线分别为x轴,y轴,
z轴,建立如图所示坐标系.
若选条件①:
方法1:过点B作BM^AC,交AC于点M,
因为PA^底面ABCD,BM⊂平面ABC,
所以PA^ BM,
7因为AC∩PA=A,
所以BM^平面PAC,
又点B到平面PAC的距离为1,所以BM=1,
在Rt△ABC中,AC=2,所以 .
因此 , , ,
又 , ,
所以 , .
设 是平面PBC的法向量,则 , ,即
取 ,则 , ,所以 是平面PBC的一个法向量.
因为BM^平面PAC,所以 是平面PAC的一个法向量.
设平面ACP与平面BCP的夹角为 ,则
,
所以平面ACP与平面BCP夹角的余弦值为 .
方法2: , ,设 ,则
可求得平面PAC的法向量为 ,则
,得 .以下同方法1
若选条件②:
方法1:由(Ⅰ)知BC^平面PAB,
因为直线PC与平面PAB所成角的大小为30°,
所以 即为PC与平面PAB所成的角,即 =30°.
在Rt△PAC中,AC=PA=2,所以 ,
在Rt△PBC中, , =30°,所以 ,
方法2:由条件①方法2得到 ,
是平面的PAB的一个法向量,
8所以 ,得 .以下同条件①. …………………………15分
20.(本小题15分)
解:(Ⅰ)因为椭圆E过点(0,1),所以 ,
又因为长轴长为4,所以 ,所以 ,
所以 .
椭圆E的方程为: ,离心率 . …………………………6分
(Ⅱ)由 得: ,
由 得: 或
设点A的坐标 ,点B的坐标 ,则点D的坐标 ,
由已知得直线AD有斜率,直线AD的方程为: ,
令 得:
,
所以直线AD过定点 . …………………………15分
21.(本小题14分)
解:(Ⅰ)①,②均正确; …………………………4分
(Ⅱ)因为 ,均有
所以当 时,有 ,
所以
9,
所以 ,
当 时,有 ,
所以
,
所以 ,
所以 ,即 ,
所以 ,
整理得 . …………………………9分
(Ⅲ)由(Ⅱ)得,当 时,有 ,
所以 ,均有 ,
即 ,
所以
所以
,
即 ,
又因为 ,所以 . …………………………14分
10