文档内容
专题 1.7 空间向量与立体几何全章八类必考压轴题
【人教A版(2019)】
【考点1 空间向量的线性运算】
1
1.(2023·全国·高三对口高考) (⃗a+2⃗b−3⃗c)−3(⃗a−2⃗b−⃗c)=( )
2
5 5 5 3 5 9
A.− ⃗a−4⃗c B.− ⃗a+4⃗b−2⃗c C.− ⃗a+7⃗b+ ⃗c D.− ⃗a−5⃗b− ⃗c
2 2 2 2 2 2
2.(2023春·安徽合肥·高二校考期末)已知 , ,则 等于( )
⃗a=(1,2,1) ⃗b=(2,−4,1) 2⃗a+⃗b
A.(4,−2,0) B.(4,0,3)
C.(−4,0,3) D.(4,0,−3)
3.(2023春·高二课时练习)已知向量 , , ,则 的坐标为
⃗a=(−2,−3,1) ⃗b=(2,0,3) ⃗c=(0,0,2) ⃗a+6⃗b−⃗c
.
4.(2023春·高二课时练习)已知 , ,求 , , .
⃗a=(1,−3,8) ⃗b=(3,10,−4) ⃗a+⃗b ⃗a−⃗b 3⃗a
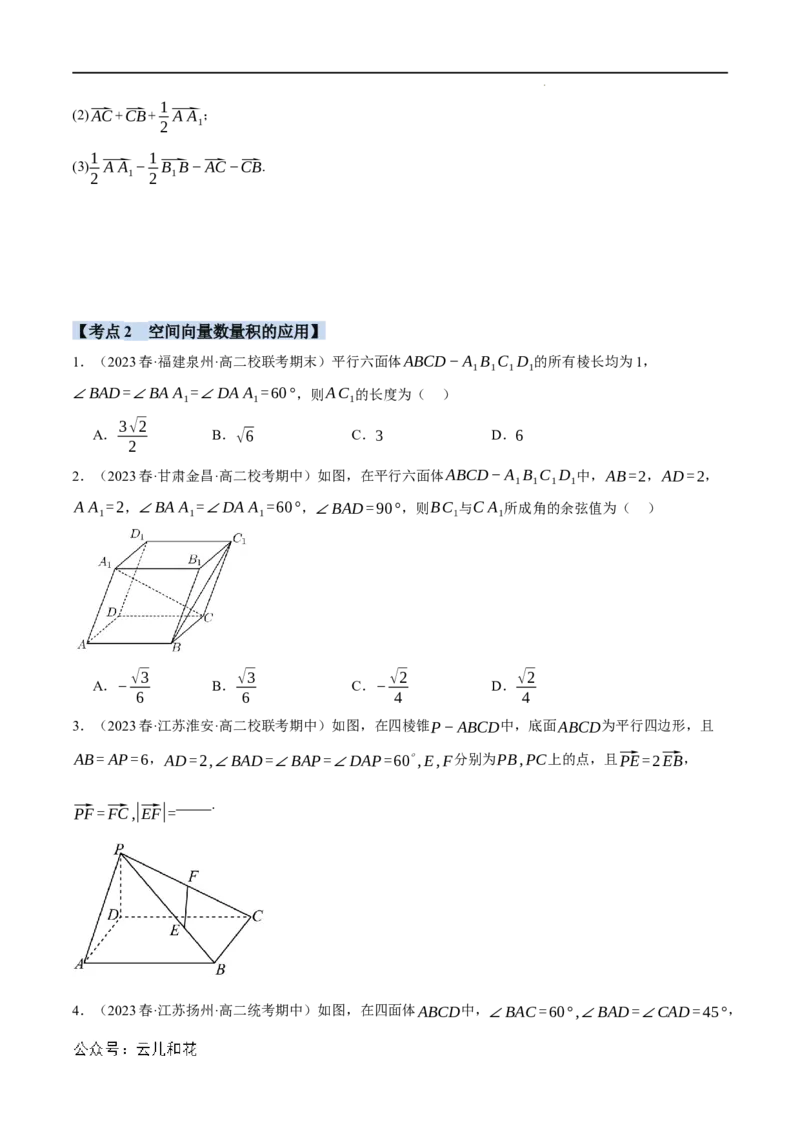
5.(2023春·高二课时练习)如图所示,在三棱柱ABC−A B C 中,M是BB 的中点,化简下列各式,
1 1 1 1
并在图中标出化简得到的向量.
(1)⃑CB+⃑BA ;
1
学科网(北京)股份有限公司1
(2)⃑AC+⃑CB+ ⃑A A ;
2 1
1 1
(3) ⃑A A − ⃑B B−⃑AC−⃑CB.
2 1 2 1
【考点2 空间向量数量积的应用】
1.(2023春·福建泉州·高二校联考期末)平行六面体ABCD−A B C D 的所有棱长均为1,
1 1 1 1
∠BAD=∠BA A =∠DA A =60°,则AC 的长度为( )
1 1 1
3√2
A. B.√6 C.3 D.6
2
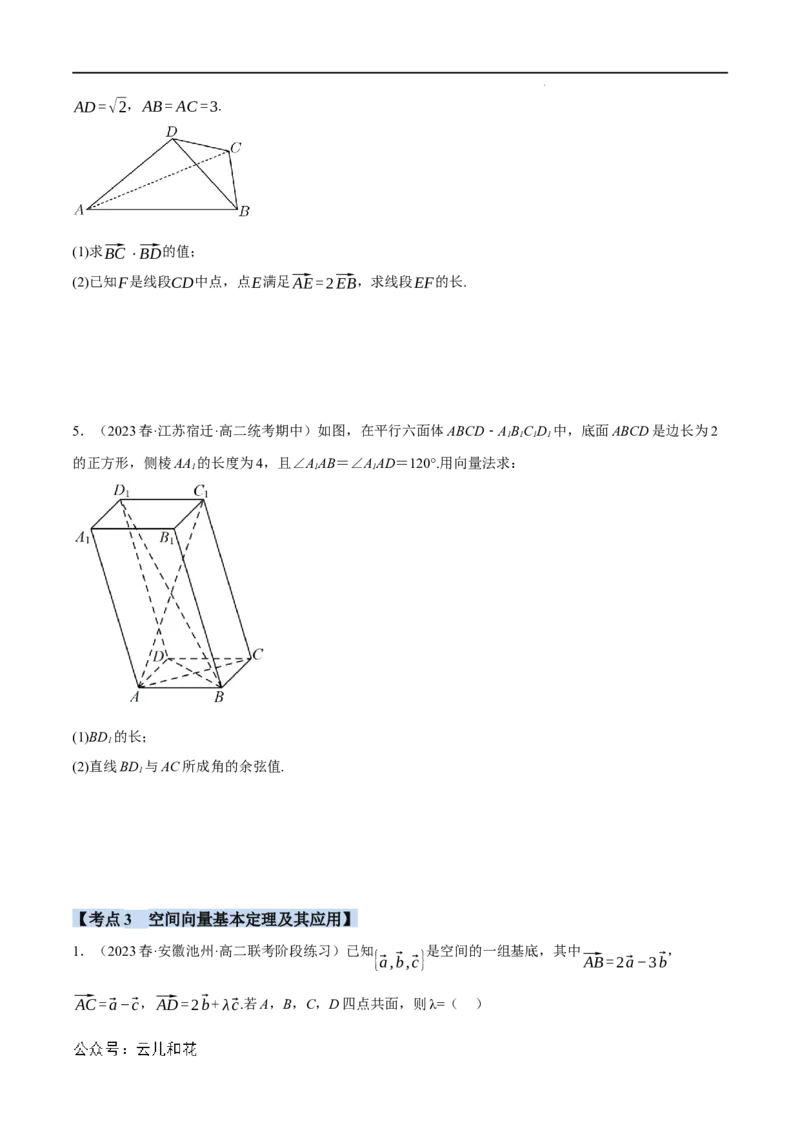
2.(2023春·甘肃金昌·高二校考期中)如图,在平行六面体ABCD−A B C D 中,AB=2,AD=2,
1 1 1 1
A A =2,∠BA A =∠DA A =60°,∠BAD=90°,则BC 与C A 所成角的余弦值为( )
1 1 1 1 1
√3 √3 √2 √2
A.− B. C.− D.
6 6 4 4
3.(2023春·江苏淮安·高二校联考期中)如图,在四棱锥P−ABCD中,底面ABCD为平行四边形,且
AB=AP=6,AD=2,∠BAD=∠BAP=∠DAP=60∘,E,F分别为PB,PC上的点,且⃗PE=2⃗EB,
.
⃗PF=⃗FC,|⃗EF|=
4.(2023春·江苏扬州·高二统考期中)如图,在四面体ABCD中,∠BAC=60°,∠BAD=∠CAD=45°,
学科网(北京)股份有限公司AD=√2,AB=AC=3.
(1)求⃗BC⋅⃗BD的值;
(2)已知F是线段CD中点,点E满足⃗AE=2⃗EB,求线段EF的长.
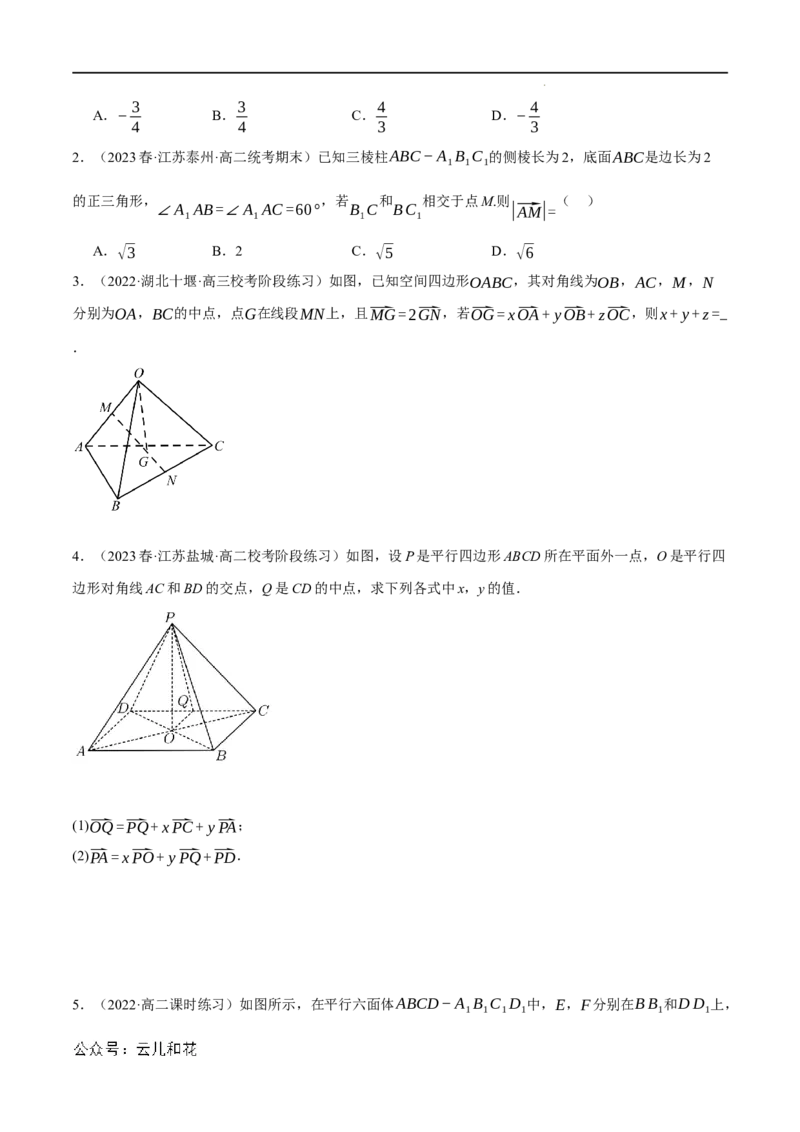
5.(2023春·江苏宿迁·高二统考期中)如图,在平行六面体ABCD﹣ABC D 中,底面ABCD是边长为2
1 1 1 1
的正方形,侧棱AA 的长度为4,且∠AAB=∠AAD=120°.用向量法求:
1 1 1
(1)BD 的长;
1
(2)直线BD 与AC所成角的余弦值.
1
【考点3 空间向量基本定理及其应用】
1.(2023春·安徽池州·高二联考阶段练习)已知 是空间的一组基底,其中 ,
{⃗a,⃗b,⃗c} ⃗AB=2⃗a−3⃗b
⃗AC=⃗a−⃗c,⃗AD=2⃗b+λ⃗c.若A,B,C,D四点共面,则λ=( )
学科网(北京)股份有限公司3 3 4 4
A.− B. C. D.−
4 4 3 3
2.(2023春·江苏泰州·高二统考期末)已知三棱柱ABC−A B C 的侧棱长为2,底面ABC是边长为2
1 1 1
的正三角形, ,若 和 相交于点M.则 ( )
∠A AB=∠A AC=60° B C BC |⃗AM|=
1 1 1 1
A.√3 B.2 C.√5 D.√6
3.(2022·湖北十堰·高三校考阶段练习)如图,已知空间四边形OABC,其对角线为OB,AC,M,N
分别为OA,BC的中点,点G在线段MN上,且⃑MG=2⃑GN,若⃑OG=x⃑OA+ y⃑OB+z⃑OC,则x+ y+z=
.
4.(2023春·江苏盐城·高二校考阶段练习)如图,设P是平行四边形ABCD所在平面外一点,O是平行四
边形对角线AC和BD的交点,Q是CD的中点,求下列各式中x,y的值.
(1)⃑OQ=⃑PQ+x⃑PC+ y⃑PA;
(2)⃑PA=x⃑PO+ y⃑PQ+⃑PD.
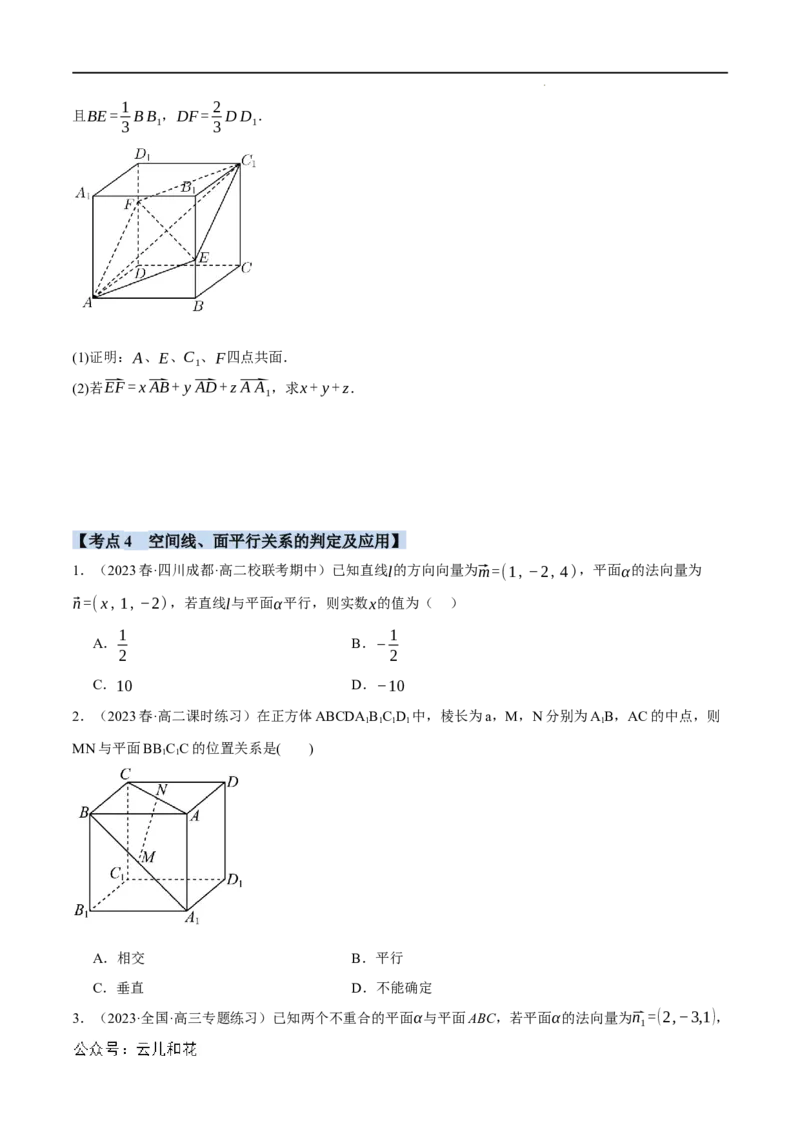
5.(2022·高二课时练习)如图所示,在平行六面体ABCD−A B C D 中,E,F分别在BB 和DD 上,
1 1 1 1 1 1
学科网(北京)股份有限公司1 2
且BE= BB ,DF= DD .
3 1 3 1
(1)证明:A、E、C 、F四点共面.
1
(2)若⃑EF=x⃑AB+ y⃑AD+z⃑A A ,求x+ y+z.
1
【考点4 空间线、面平行关系的判定及应用】
1.(2023春·四川成都·高二校联考期中)已知直线l的方向向量为⃗m=(1,−2,4),平面α的法向量为
⃗n=(x,1,−2),若直线l与平面α平行,则实数x的值为( )
1 1
A. B.−
2 2
C.10 D.−10
2.(2023春·高二课时练习)在正方体ABCDAB C D 中,棱长为a,M,N分别为AB,AC的中点,则
1 1 1 1 1
MN与平面BB C C的位置关系是( )
1 1
A.相交 B.平行
C.垂直 D.不能确定
3.(2023·全国·高三专题练习)已知两个不重合的平面α与平面ABC,若平面α的法向量为⃑n =(2,−3,1),
1
学科网(北京)股份有限公司⃑AB=(1,0,−2),⃑AC=(1,1,1),则平面α和平面ABC的位置关系是 .
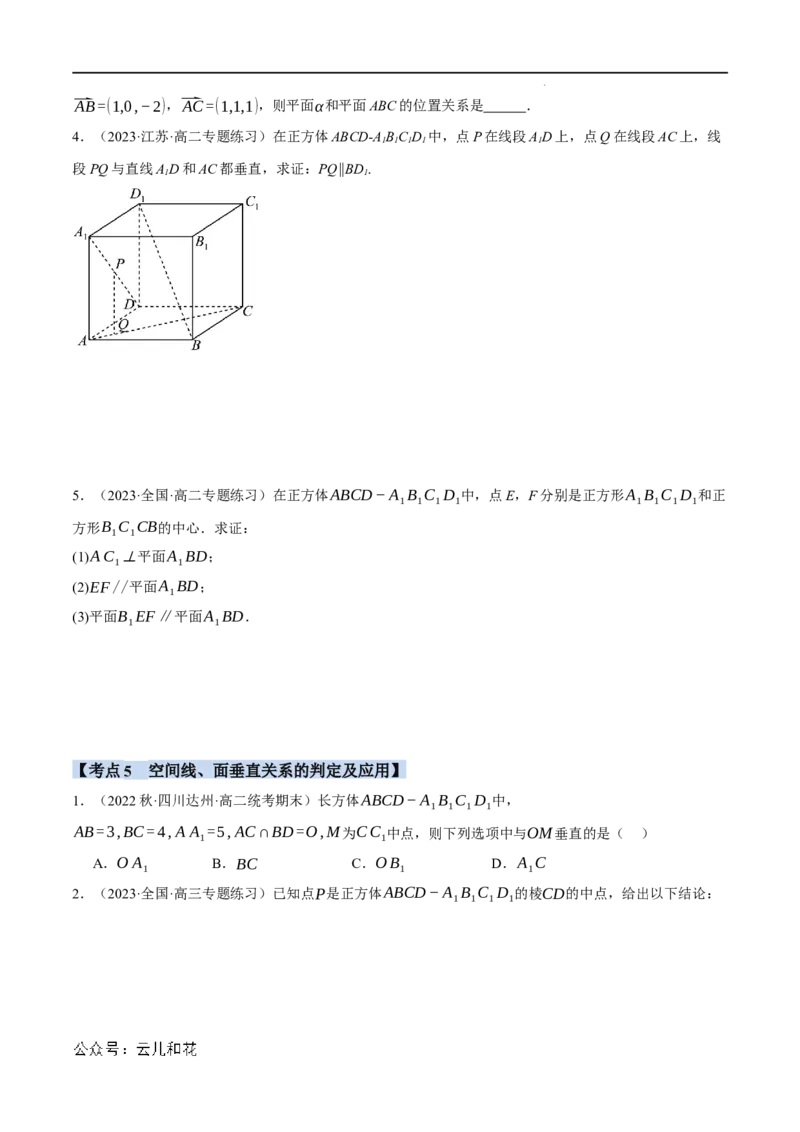
4.(2023·江苏·高二专题练习)在正方体ABCD-ABC D 中,点P在线段AD上,点Q在线段AC上,线
1 1 1 1 1
段PQ与直线AD和AC都垂直,求证:PQ∥BD.
1 1
5.(2023·全国·高二专题练习)在正方体ABCD−A B C D 中,点E,F分别是正方形A B C D 和正
1 1 1 1 1 1 1 1
方形B C CB的中心.求证:
1 1
(1)AC ⊥平面A BD;
1 1
(2)EF//平面A BD;
1
(3)平面B EF∥平面A BD.
1 1
【考点5 空间线、面垂直关系的判定及应用】
1.(2022秋·四川达州·高二统考期末)长方体ABCD−A B C D 中,
1 1 1 1
AB=3,BC=4,A A =5,AC∩BD=O,M为CC 中点,则下列选项中与OM垂直的是( )
1 1
A.OA B.BC C.OB D.A C
1 1 1
2.(2023·全国·高三专题练习)已知点P是正方体ABCD−A B C D 的棱CD的中点,给出以下结论:
1 1 1 1
学科网(北京)股份有限公司①A P⊥C D;
1 1
②A P⊥BD;
1
③A P⊥BC ;
1 1
④A P⊥平面BC D
1 1
其中正确命题的序号是( )
A.① B.② C.③ D.④
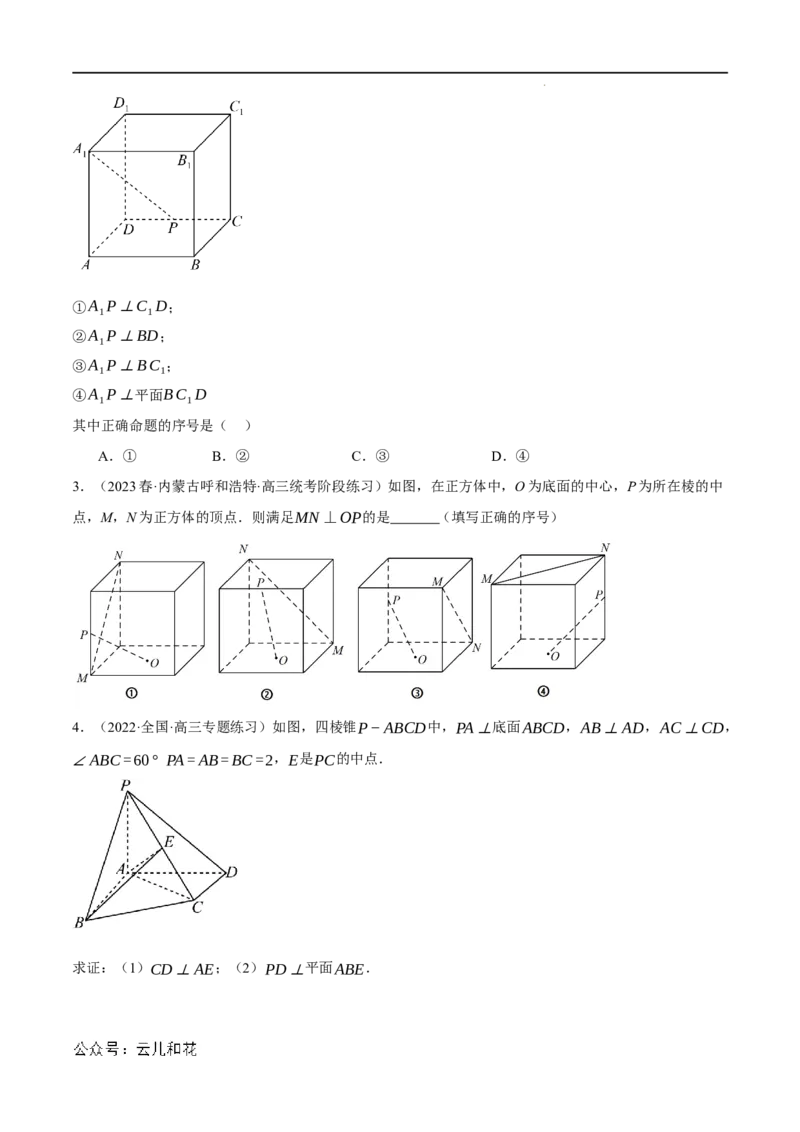
3.(2023春·内蒙古呼和浩特·高三统考阶段练习)如图,在正方体中,O为底面的中心,P为所在棱的中
点,M,N为正方体的顶点.则满足MN⊥OP的是 (填写正确的序号)
4.(2022·全国·高三专题练习)如图,四棱锥P−ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,
∠ABC=60° PA=AB=BC=2,E是PC的中点.
求证:(1)CD⊥AE;(2)PD⊥平面ABE.
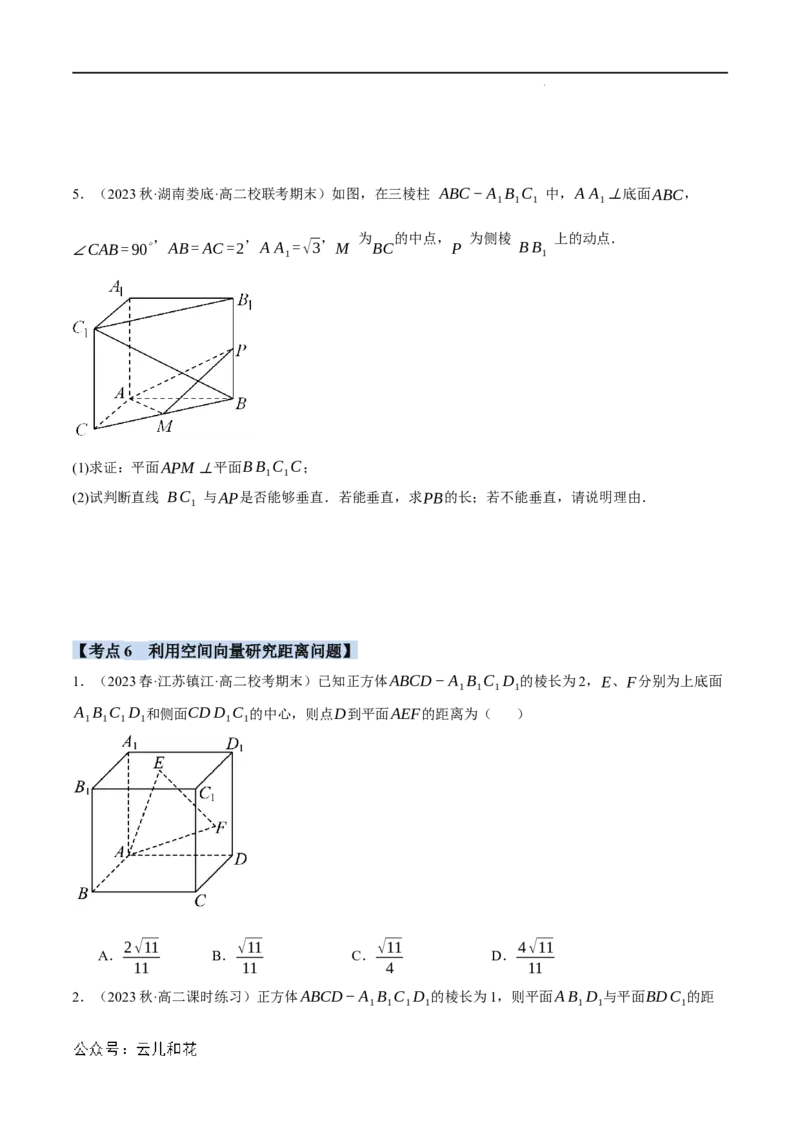
学科网(北京)股份有限公司5.(2023秋·湖南娄底·高二校联考期末)如图,在三棱柱 ABC−A B C 中,A A ⊥底面ABC,
1 1 1 1
, , , 为 的中点, 为侧棱 上的动点.
∠CAB=90∘ AB=AC=2 A A =√3 M BC P BB
1 1
(1)求证:平面APM⊥平面BB C C;
1 1
(2)试判断直线 BC 与AP是否能够垂直.若能垂直,求PB的长;若不能垂直,请说明理由.
1
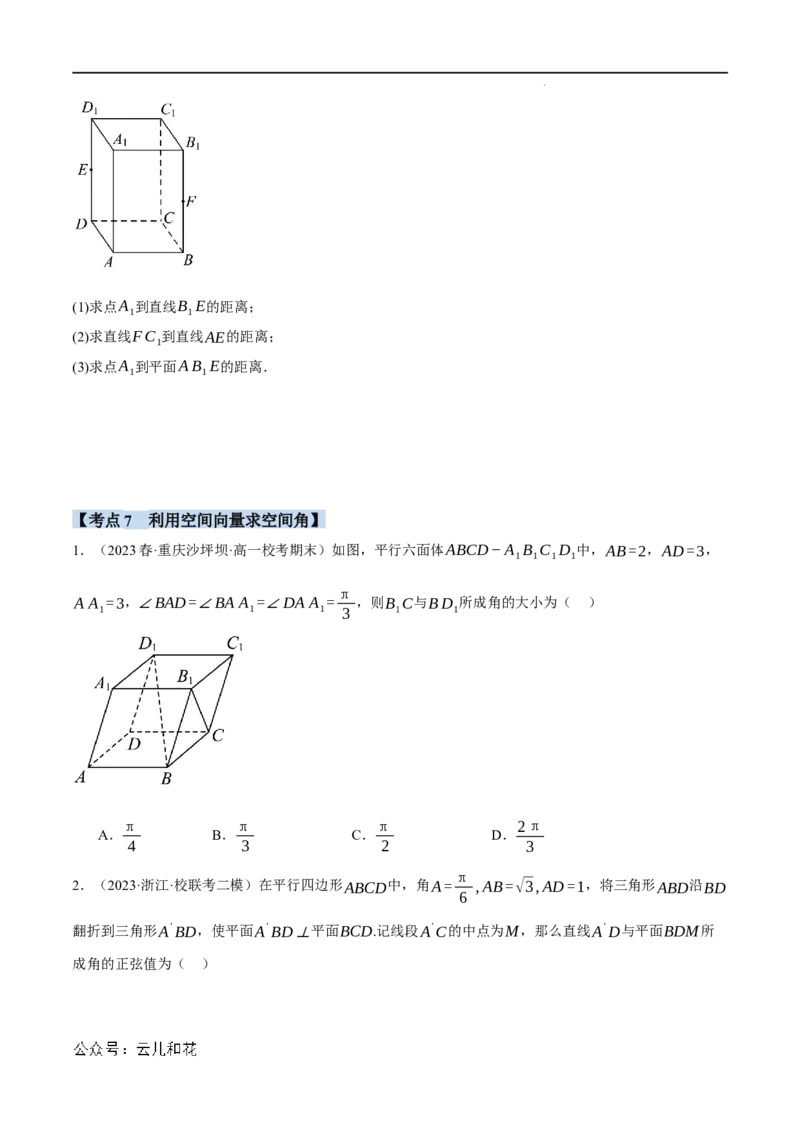
【考点6 利用空间向量研究距离问题】
1.(2023春·江苏镇江·高二校考期末)已知正方体ABCD−A B C D 的棱长为2,E、F分别为上底面
1 1 1 1
A B C D 和侧面CDD C 的中心,则点D到平面AEF的距离为( )
1 1 1 1 1 1
2√11 √11 √11 4√11
A. B. C. D.
11 11 4 11
2.(2023秋·高二课时练习)正方体ABCD−A B C D 的棱长为1,则平面AB D 与平面BDC 的距
1 1 1 1 1 1 1
学科网(北京)股份有限公司离为( )
√2 √3
A.√2 B.√3 C. D.
3 3
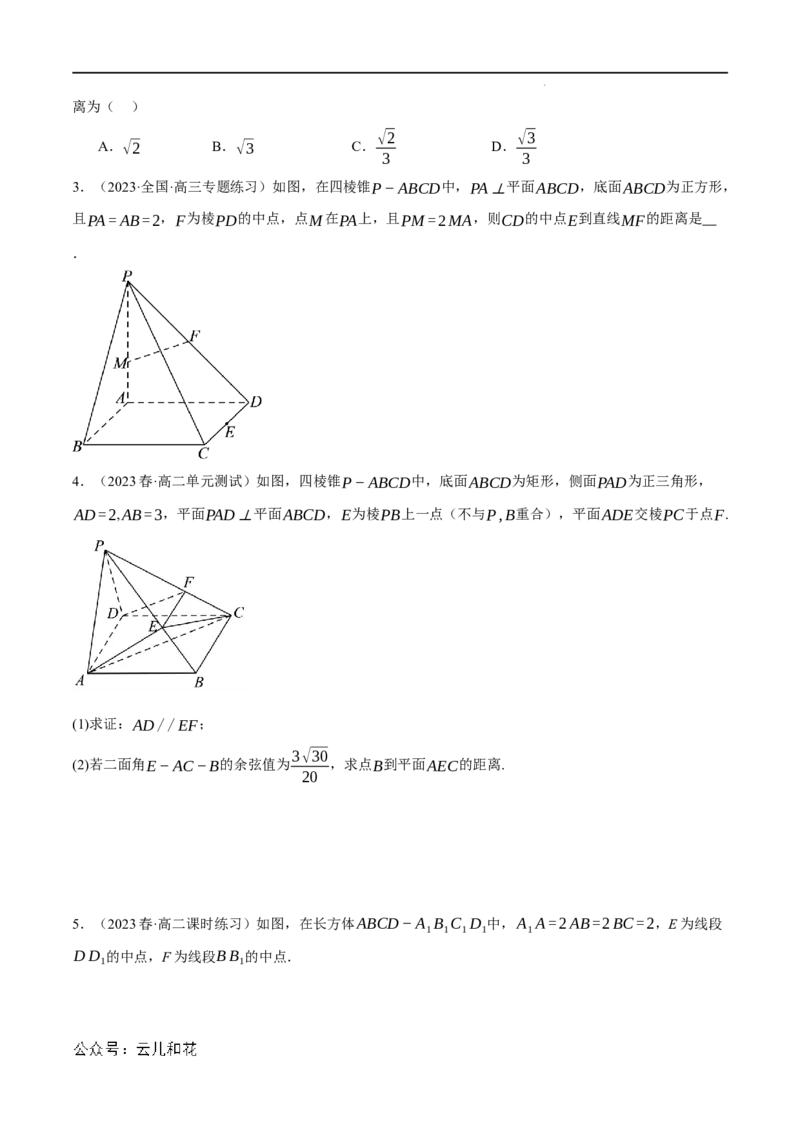
3.(2023·全国·高三专题练习)如图,在四棱锥P−ABCD中,PA⊥平面ABCD,底面ABCD为正方形,
且PA=AB=2,F为棱PD的中点,点M在PA上,且PM=2MA,则CD的中点E到直线MF的距离是
.
4.(2023春·高二单元测试)如图,四棱锥P−ABCD中,底面ABCD为矩形,侧面PAD为正三角形,
AD=2,AB=3,平面PAD⊥平面ABCD,E为棱PB上一点(不与P,B重合),平面ADE交棱PC于点F.
(1)求证:AD//EF;
3√30
(2)若二面角E−AC−B的余弦值为 ,求点B到平面AEC的距离.
20
5.(2023春·高二课时练习)如图,在长方体ABCD−A B C D 中,A A=2AB=2BC=2,E为线段
1 1 1 1 1
DD 的中点,F为线段BB 的中点.
1 1
学科网(北京)股份有限公司(1)求点A 到直线B E的距离;
1 1
(2)求直线FC 到直线AE的距离;
1
(3)求点A 到平面AB E的距离.
1 1
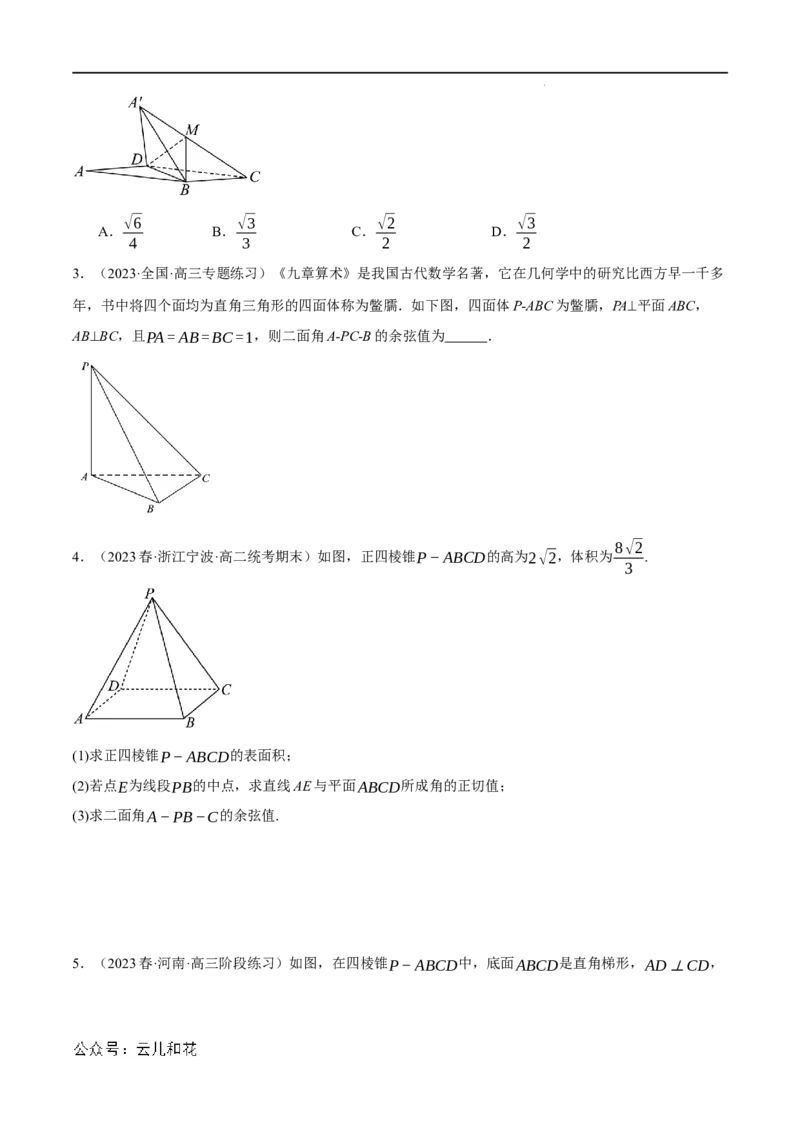
【考点7 利用空间向量求空间角】
1.(2023春·重庆沙坪坝·高一校考期末)如图,平行六面体ABCD−A B C D 中,AB=2,AD=3,
1 1 1 1
π
A A =3,∠BAD=∠BA A =∠DA A = ,则B C与BD 所成角的大小为( )
1 1 1 3 1 1
π π π 2π
A. B. C. D.
4 3 2 3
π
2.(2023·浙江·校联考二模)在平行四边形ABCD中,角A= ,AB=√3,AD=1,将三角形ABD沿BD
6
翻折到三角形A′BD,使平面A′BD⊥平面BCD.记线段A′C的中点为M,那么直线A′D与平面BDM所
成角的正弦值为( )
学科网(北京)股份有限公司√6 √3 √2 √3
A. B. C. D.
4 3 2 2
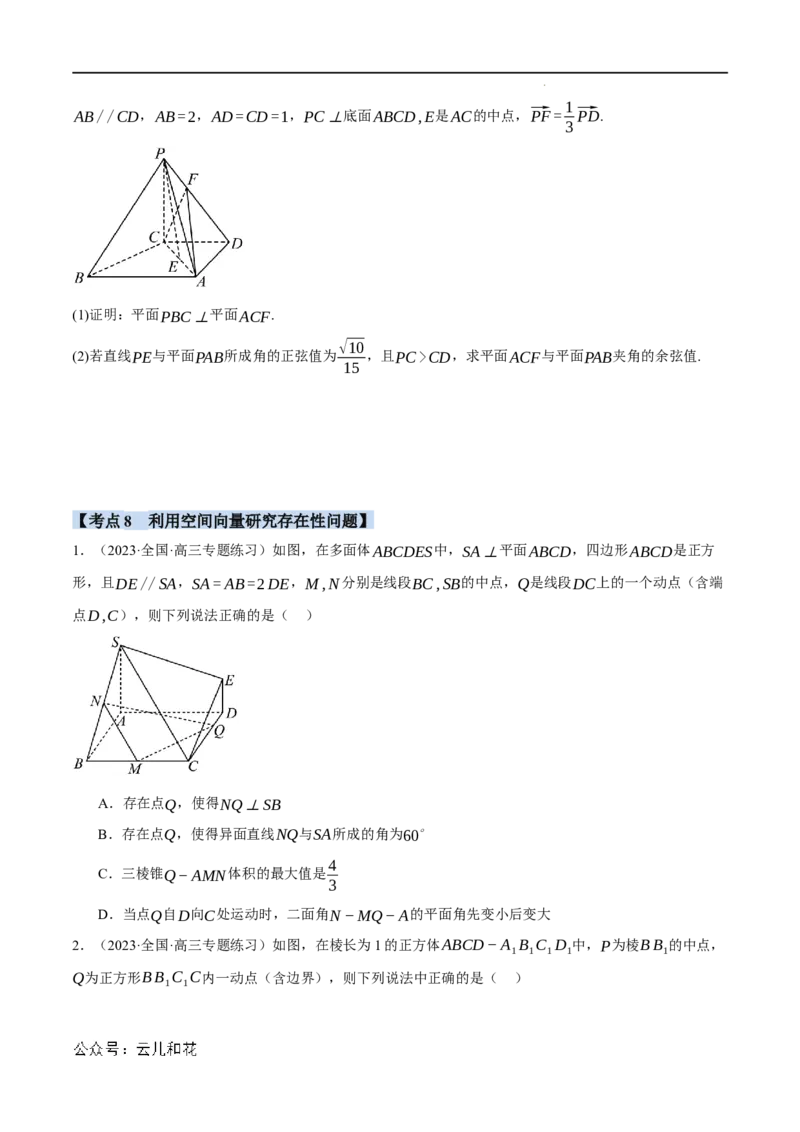
3.(2023·全国·高三专题练习)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多
年,书中将四个面均为直角三角形的四面体称为鳖臑.如下图,四面体P-ABC为鳖臑,PA⊥平面ABC,
AB⊥BC,且PA=AB=BC=1,则二面角A-PC-B的余弦值为 .
8√2
4.(2023春·浙江宁波·高二统考期末)如图,正四棱锥P−ABCD的高为2√2,体积为 .
3
(1)求正四棱锥P−ABCD的表面积;
(2)若点E为线段PB的中点,求直线AE与平面ABCD所成角的正切值;
(3)求二面角A−PB−C的余弦值.
5.(2023春·河南·高三阶段练习)如图,在四棱锥P−ABCD中,底面ABCD是直角梯形,AD⊥CD,
学科网(北京)股份有限公司1
AB//CD,AB=2,AD=CD=1,PC⊥底面ABCD,E是AC的中点,⃗PF= ⃗PD.
3
(1)证明:平面PBC⊥平面ACF.
√10
(2)若直线PE与平面PAB所成角的正弦值为 ,且PC>CD,求平面ACF与平面PAB夹角的余弦值.
15
【考点8 利用空间向量研究存在性问题】
1.(2023·全国·高三专题练习)如图,在多面体ABCDES中,SA⊥平面ABCD,四边形ABCD是正方
形,且DE//SA,SA=AB=2DE,M,N分别是线段BC,SB的中点,Q是线段DC上的一个动点(含端
点D,C),则下列说法正确的是( )
A.存在点Q,使得NQ⊥SB
B.存在点Q,使得异面直线NQ与SA所成的角为60∘
4
C.三棱锥Q−AMN体积的最大值是
3
D.当点Q自D向C处运动时,二面角N−MQ−A的平面角先变小后变大
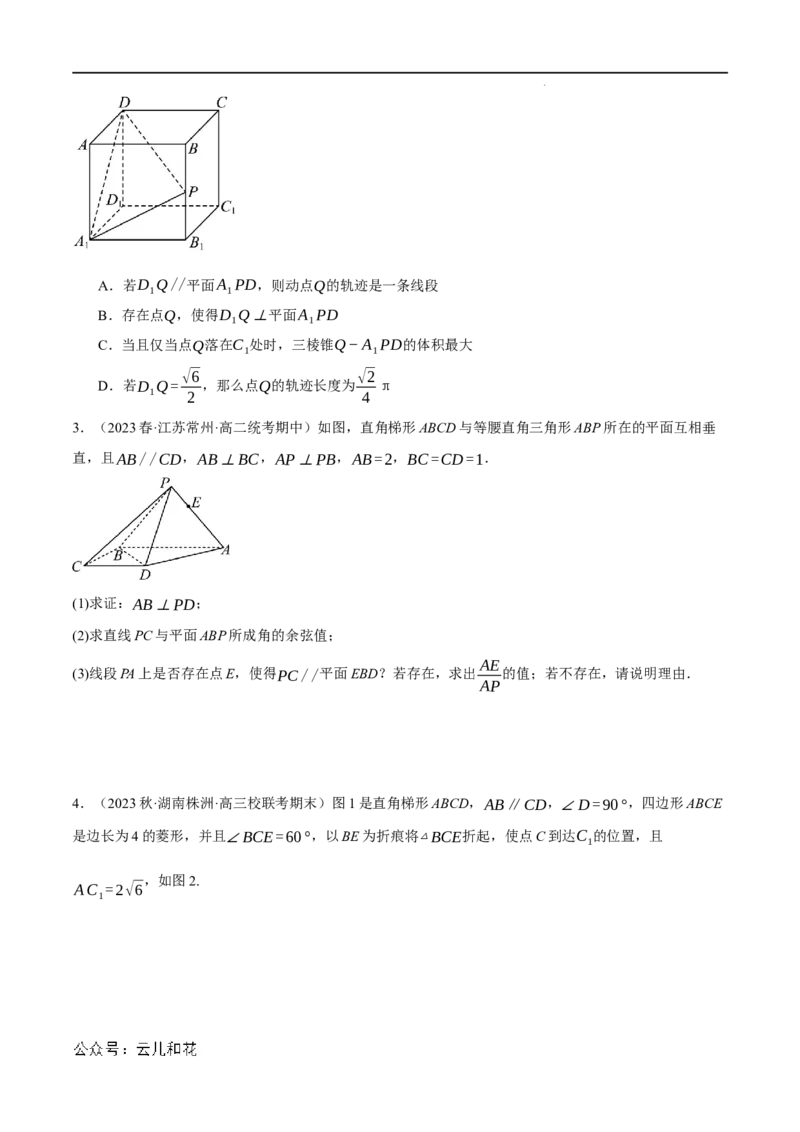
2.(2023·全国·高三专题练习)如图,在棱长为1的正方体ABCD−A B C D 中,P为棱BB 的中点,
1 1 1 1 1
Q为正方形BB C C内一动点(含边界),则下列说法中正确的是( )
1 1
学科网(北京)股份有限公司A.若D Q//平面A PD,则动点Q的轨迹是一条线段
1 1
B.存在点Q,使得D Q⊥平面A PD
1 1
C.当且仅当点Q落在C 处时,三棱锥Q−A PD的体积最大
1 1
√6 √2
D.若D Q= ,那么点Q的轨迹长度为 π
1 2 4
3.(2023春·江苏常州·高二统考期中)如图,直角梯形ABCD与等腰直角三角形ABP所在的平面互相垂
直,且AB//CD,AB⊥BC,AP⊥PB,AB=2,BC=CD=1.
(1)求证:AB⊥PD;
(2)求直线PC与平面ABP所成角的余弦值;
AE
(3)线段PA上是否存在点E,使得PC//平面EBD?若存在,求出 的值;若不存在,请说明理由.
AP
4.(2023秋·湖南株洲·高三校联考期末)图1是直角梯形ABCD,AB∥CD,∠D=90°,四边形ABCE
是边长为4的菱形,并且∠BCE=60°,以BE为折痕将△BCE折起,使点C到达C 的位置,且
1
,如图2.
AC =2√6
1
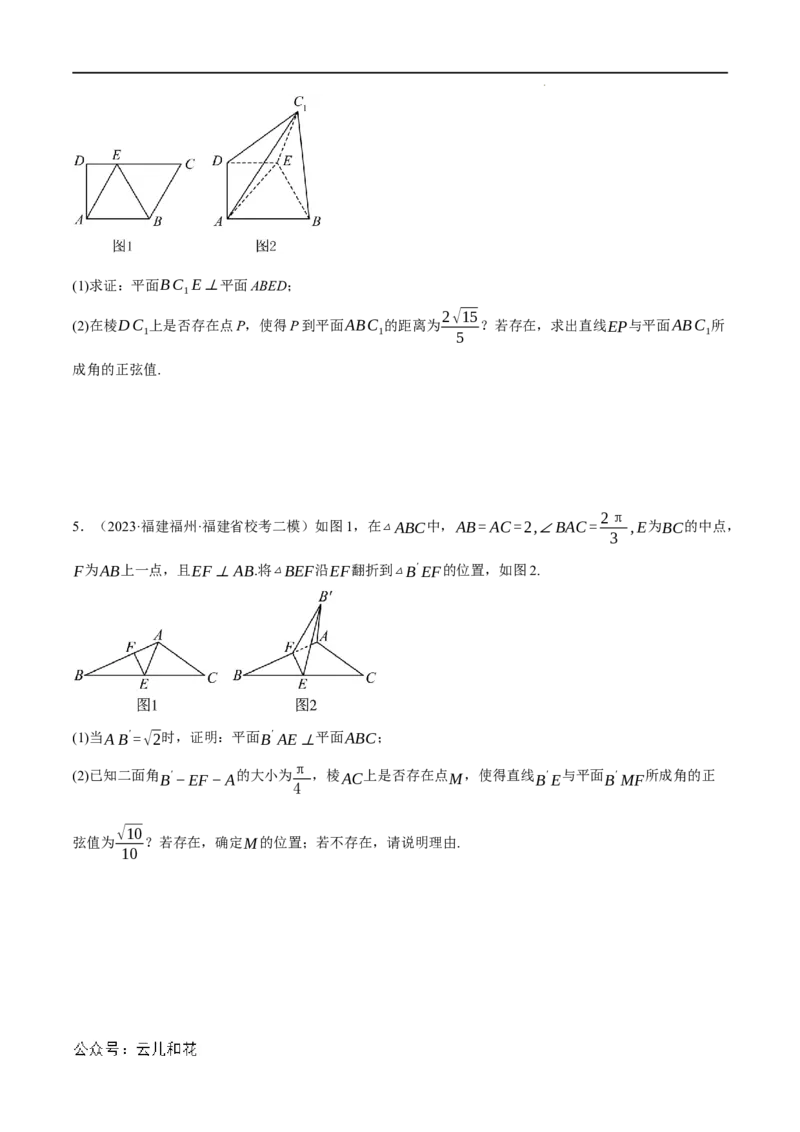
学科网(北京)股份有限公司(1)求证:平面BC E⊥平面ABED;
1
2√15
(2)在棱DC 上是否存在点P,使得P到平面ABC 的距离为 ?若存在,求出直线EP与平面ABC 所
1 1 5 1
成角的正弦值.
2π
5.(2023·福建福州·福建省校考二模)如图1,在△ABC中,AB=AC=2,∠BAC= ,E为BC的中点,
3
F为AB上一点,且EF⊥AB.将△BEF沿EF翻折到△B′EF的位置,如图2.
(1)当AB′=√2时,证明:平面B′ AE⊥平面ABC;
π
(2)已知二面角 B′−EF−A 的大小为 ,棱AC上是否存在点M,使得直线 B′E 与平面 B′MF 所成角的正
4
√10
弦值为 ?若存在,确定M的位置;若不存在,请说明理由.
10
学科网(北京)股份有限公司