文档内容
第一章 空间向量与立体几何全章综合测试卷(提高篇)
参考答案与试题解析
一.选择题(共8小题,满分40分,每小题5分)
1.(5分)(2023秋·河北保定·高二统考期末)在以下命题中:
①三个非零向量⃗a,⃗b,⃗c不能构成空间的一个基底,则⃗a,⃗b,⃗c共面;
②若两个非零向量⃗a,⃗b与任何一个向量都不能构成空间的一个基底,则⃗a,⃗b共线;
③对空间任意一点O和不共线的三点A,B,C,若⃗OP=2⃗OA−⃗2OB−⃗2OC,则P,A,B,C四点共面
④若⃗a,⃗b是两个不共线的向量,且⃗c=λ⃗a+μ⃗b(λ,μ∈R,λ,μ≠0),则{⃗a,⃗b,⃗c}构成空间的一个基底
⑤若{⃗a,⃗b,⃗c}为空间的一个基底,则{⃗a+⃗b,⃗b+⃗c+2⃗a,⃗c+⃗a}构成空间的另一个基底;其中真命题的个数是
( )
A.0 B.1 C.2 D.3
【解题思路】直接利用空间基底,共面向量,共线向量的基础知识的应用求出结果.
【解答过程】空间任意三个不共面的向量都可以作为空间的一个基底.
①根据空间基底的定义,三个非零向量⃗a,⃗b,⃗c不能构成空间的一个基底,则⃗a,⃗b,⃗c共面;故命题①正
确.
②由空间基底的定义,若两个非零向量⃗a,⃗b与任何一个向量都不能构成空间的一个基底,则⃗a,⃗b共线,
若⃗a,⃗b不共线,则⃗a,⃗b共面,一定有向量与⃗a,⃗b不共面;故命题②正确.
③对空间任意一点O和不共线的三点A,B,C,当⃗OP=2⃗OA−⃗2OB−⃗2OC时,若P,A,B,C四点共
面,则⃗AP=λ⃗AB+μ⃗AC,⃗OP−⃗OA=λ(⃗OB−⃗OA)+μ(⃗OC−⃗OA),⃗OP=(1−λ−μ)⃗OA+λ⃗OB+μ⃗OC,
¿,方程组无解,故P,A,B,C四点不共面;故命题③错误.
④若⃗a,⃗b是两个不共线的向量,且⃗c=λ⃗a+μ⃗b(λ,μ∈R,λ,μ≠0),则向量⃗c与⃗a,⃗b构成共面向量,
{⃗a,⃗b,⃗c}不能构成空间的一个基底;故命题④错误.
⑤利用反证法:若{⃗a+⃗b,⃗b+⃗c,⃗c+⃗a}不能构成空间的一个基底,则这三个向量共面,
1−y 1−x
设⃗a+⃗b=x(⃗b+⃗c)+ y(⃗c+⃗a)(x,y∈R),当x+ y=0,⃗a与⃗b共线,当x+ y≠0,得⃗c= ⃗a+ ⃗b,
x+ y x+ y
学科网(北京)股份有限公司都有⃗a,⃗b,⃗c共面,由于{⃗a,⃗b,⃗c}为空间的一个基底,得出矛盾,所以{⃗a+⃗b,⃗b+⃗c,⃗c+⃗a}能够成空间的一个
基底,故命题⑤正确.
真命题有3个.
故选:D.
2.(5分)(2023·全国·高三专题练习)已知MN是棱长为4的正方体内切球的一条直径,点P在正方体
表面上运动,则⃑PM⋅⃑PN的最大值为( )
A.4 B.12 C.8 D.6
【解题思路】设正方体内切球的球心为O,则⃑OM=−⃑ON,⃑PM⋅⃑PN=(⃑OM−⃑OP)⋅(⃑ON−⃑OP)
=|⃑OP| 2 −4,将问题转化为求|⃑OP|的最大值.
【解答过程】设正方体内切球的球心为O,则|OM|=|ON|=2,⃑OM=−⃑ON,
2 2
∴⃑PM⋅⃑PN=(⃑OM−⃑OP)⋅(⃑ON−⃑OP)=|⃑OP| −⃑OP⋅(⃑OM+⃑ON)+⃑OM⋅⃑ON==|⃑OP| −4,
又点P在正方体表面上运动,∴当P为正方体顶点时,|⃑OP|最大,且最大值为正方体体对角线的一半,
1
|⃑OP| = ×√3×42= 2√3,∴⃑PM⋅⃑PN的最大值为(2√3) 2 −4=8.
max 2
故选:C.
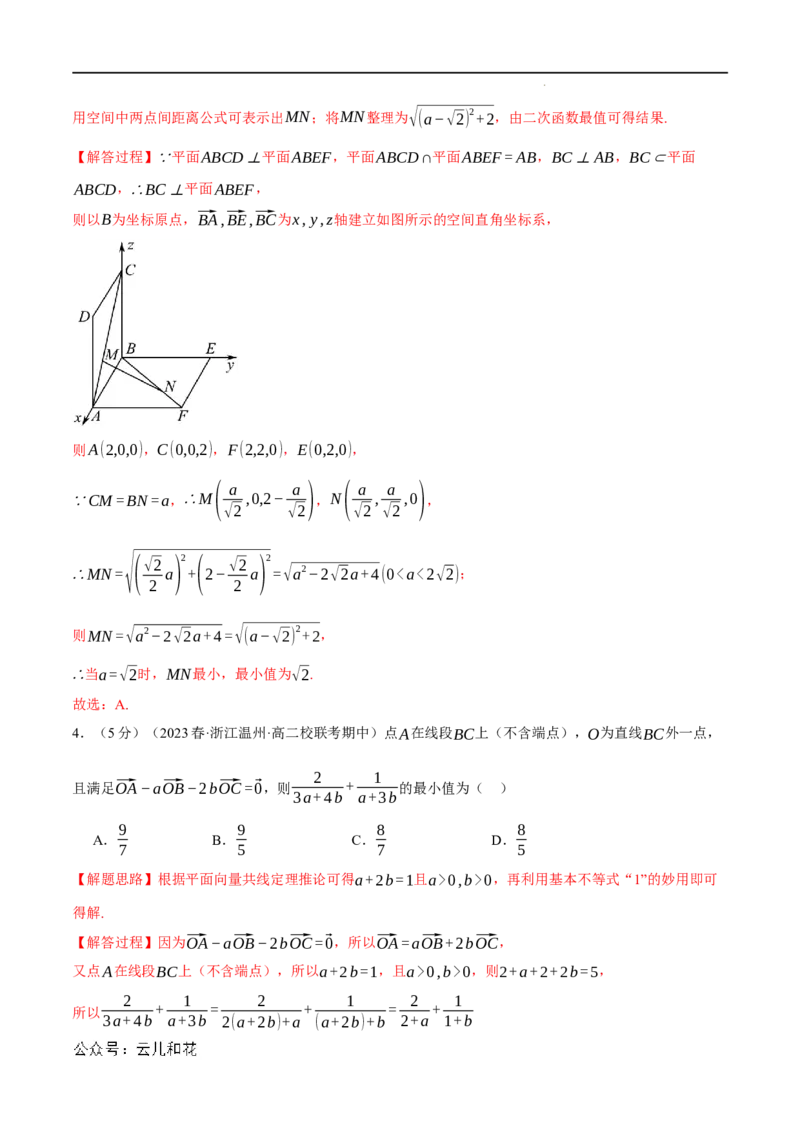
3.(5分)(2023春·江苏徐州·高二统考期中)在如图所示的试验装置中,两个正方形框架ABCD,ABEF
的边长都是2,且它们所在的平面互相垂直,活动弹子M,N分别在正方形对角线AC和BF上移动,且
CM和BN的长度保持相等,记CM=BN=a,其中00,b>0,再利用基本不等式“1”的妙用即可
得解.
【解答过程】因为⃗OA−a⃗OB−2b⃗OC=0⃗,所以⃗OA=a⃗OB+2b⃗OC,
又点A在线段BC上(不含端点),所以a+2b=1,且a>0,b>0,则2+a+2+2b=5,
2 1 2 1 2 1
+ = + = +
所以
3a+4b a+3b 2(a+2b)+a (a+2b)+b 2+a 1+b
学科网(北京)股份有限公司2 2 1
= + = (2+a+2+2b)¿
2+a 2+2b 5
1[ 2(2+a) 2(2+2b)] 1[ √2(2+a) 2(2+2b)] 8
= 4+ + ≥ 4+2 ⋅ = ,
5 2+2b 2+a 5 2+2b 2+a 5
当且仅当¿,即¿时,等号成立,
2 1 8
故 + 的最小值为 .
3a+4b a+3b 5
故选:D.
5.(5分)(2023春·高二课时练习)设空间两个单位向量⃗OA=(m,n,0),⃗OB=(0,n,p)与向量
π
⃗OC=(1,1,1)的夹角都等于 ,则cos∠AOB=( )
4
2−√3 2+√3
A. B.
4 2
2−√3 2+√3 2−√3 2+√3
C. 或 D. 或
4 4 2 2
π √6
【解题思路】首先根据⃗OA为单位向量得到m2+n2=1,再利用⃗OA与⃗OC的夹角等于 ,得m+n= .联立
4 2
方程求解出m与n的值,最后再利用向量的夹角公式进行求解即可.
π
【解答过程】∵空间两个单位向量⃗OA=(m,n,0),⃗OB=(0,n,p)与向量⃗OC=(1,1,1)的夹角都等于 ,
4
π
∴∠AOC=∠BOC= ,|⃗OC|=√3,
4
√6
∵⃗OA⋅⃗OC=|⃗OA|⋅|⃗OC|⋅cos∠AOC= ,
2
√6
又⃗OA⋅⃗OC=m+n,∴m+n= ,
2
又⃗OA为单位向量,∴m2+n2=1,
联立¿,得¿或¿,
∵ ⃗OA=(m,n,0),⃗OB=(0,n,p),
2±√3
∴cos∠AOB=n2=
.
4
故选:C.
6.(5分)(2023春·高二课时练习)在四棱锥P−ABCD中,底面ABCD是直角梯形,AD//BC,
学科网(北京)股份有限公司AB⊥BC,侧面PAB⊥底面ABCD.若PA=AD=AB=kBC(01,与k∈(0,1)矛盾,故D错误,
cosθ cosθ
故选:A.
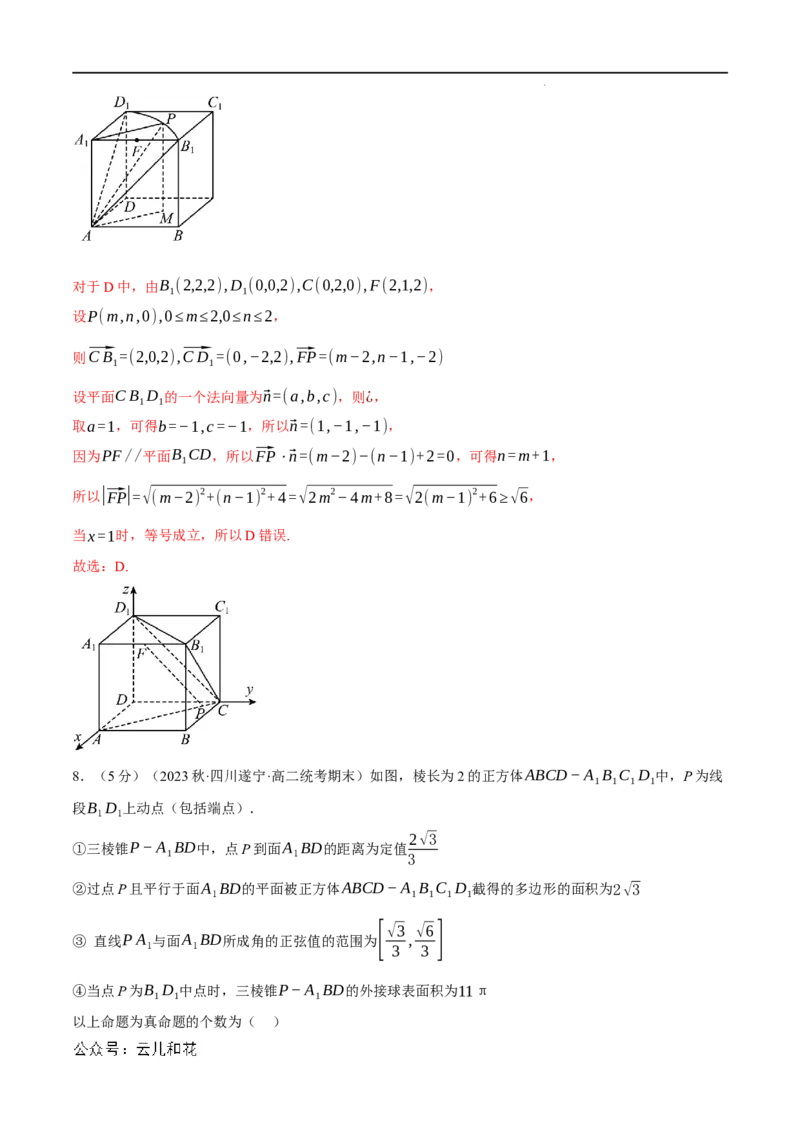
7.(5分)(2023·陕西咸阳·校考模拟预测)如图,点P是棱长为2的正方体ABCD−A B C D 的表面
1 1 1 1
上一个动点,则以下不正确的是( )
A.当P在平面BCC B 上运动时,四棱锥P−A A D D的体积不变
1 1 1 1
[π π]
B.当P在线段AC上运动时,D P与A C 所成角的取值范围是 ,
1 1 1 3 2
C.使直线AP与平面ABCD所成的角为45o的点P的轨迹长度为π+4√2
D.若F是A B 的中点,当P在底面ABCD上运动,且满足PF//平面B CD 时,PF长度的最小值是
1 1 1 1
√5
【解题思路】由底面正方形ADD A 的面积不变,点P到平面A A D D的距离不变,可判定A正确;
1 1 1 1
以D为原点,建立空间直角坐标系,设P(x,2−x,0),则⃗D P=(x,2−x,−2),⃗A C =(−2,2,0),结合
1 1 1
向量的夹角公式,可判定B正确;
由直线AP与平面ABCD所成的角为45∘,作PM⊥平面ABCD,得到点P的轨迹,可判定C正确;
设P(m,m,0),求得平面CB D 的一个法向量为⃗n=(1,−1,−1),得到|⃗FP|=√2(x−1) 2+6,可判定D
1 1
错误.
【解答过程】对于A中:底面正方形ADD A 的面积不变,点P到平面A A D D的距离为正方体棱长,
1 1 1 1
所以四棱锥P−A A D D的体积不变,所以A选项正确;
1 1
对于B中:以D为原点,DA,DC,DD 所在的直线分别为x轴、y轴和z轴,建立空间直角坐标系,可得
1
A (2,0,2),D (0,0,2),C (0,2,2),
1 1 1
设P(x,2−x,0),0≤x≤2,则⃗D P=(x,2−x,−2),⃗A C =(−2,2,0),
1 1 1
学科网(北京)股份有限公司|⃗D P⋅⃗A C | |x−1|
设直线D P与A C 所成角为θ,则cosθ=cos⟨⃗D P,⃗A C ⟩= 1 1 1 = ,
1 1 1 1 1 1 |⃗D P||⃗A C | √(x−1) 2+3
1 1 1
π
因为0≤|x−1|≤1,当|x−1|=0时,可得cosθ=0,所以θ=
;
2
|x−1| 1 1
cosθ= = ≤ π π
当0<|x−1|≤1时, √(x−1) 2+3 √ 3 2 ,所以 ≤θ< ,
1+ 3 2
2
|x−1|
[π π]
所以异面直线D P与A C 所成角的取值范围是 , ,所以B正确;
1 1 1 3 2
对于C中:因为直线AP与平面ABCD所成的角为45∘,
若点P在平面DCC D 和平面BCC B 内,
1 1 1 1
因为∠B AB=45∘,∠D AD=45∘最大,不成立;
1 1
在平面ADD A 内,点P的轨迹是AD =2√2;
1 1 1
在平面ABB A 内,点P的轨迹是AB =2√2;
1 1 1
在平面A B C D 时,作PM⊥平面ABCD,如图所示,
1 1 1 1
因为∠PAM=45∘,所以PM=AM,又因为PM=AB,所以AM=AB,所以A P=AB,
1
所以点P的轨迹是以A 点为圆心,以2为半径的四分之一圆,
1
1
所以点P的轨迹的长度为 ×2π×2=π,
4
综上,点P的轨迹的总长度为π+4√2,所以C正确;
学科网(北京)股份有限公司对于D中,由B (2,2,2),D (0,0,2),C(0,2,0),F(2,1,2),
1 1
设P(m,n,0),0≤m≤2,0≤n≤2,
则⃗CB =(2,0,2),⃗CD =(0,−2,2),⃗FP=(m−2,n−1,−2)
1 1
设平面CB D 的一个法向量为⃗n=(a,b,c),则¿,
1 1
取a=1,可得b=−1,c=−1,所以⃗n=(1,−1,−1),
因为PF//平面B CD,所以⃗FP⋅⃗n=(m−2)−(n−1)+2=0,可得n=m+1,
1
所以|⃗FP|=√(m−2) 2+(n−1) 2+4=√2m2−4m+8=√2(m−1) 2+6≥√6,
当x=1时,等号成立,所以D错误.
故选:D.
8.(5分)(2023秋·四川遂宁·高二统考期末)如图,棱长为2的正方体ABCD−A B C D 中,P为线
1 1 1 1
段B D 上动点(包括端点).
1 1
2√3
①三棱锥P−A BD中,点P到面A BD的距离为定值
1 1 3
②过点P且平行于面A BD的平面被正方体ABCD−A B C D 截得的多边形的面积为2√3
1 1 1 1 1
[√3 √6]
③ 直线PA 与面A BD所成角的正弦值的范围为 ,
1 1 3 3
④当点P为B D 中点时,三棱锥P−A BD的外接球表面积为11π
1 1 1
以上命题为真命题的个数为( )
学科网(北京)股份有限公司A.1 B.2 C.3 D.4
【解题思路】建立空间直角坐标系,对于①③用空间向量求解;对于②可证明三角形B D C为截面多边
1 1
形,求其面积即可;对于④设球心O(x ,y ,z ),由|OA |=|OB|=|OD|=|OP|求解球心坐标即可.
0 0 0 1
【解答过程】
以A为坐标原点,分别以AB,AD,A A 为x,y,z轴建系如图:
1
A(0,0,0),B(2,0,0),D(0,2,0),A (0,0,2),B (2,0,2),D (0,2,2),
1 1 1
⃗A P=(t,2−t,0),⃗BD=(−2,2,0),⃗A B=(2,0,−2),
1 1
t
设⃗B P= ⃗B D (0≤t≤2),
1 2 1 1
t t t
则⃗AP=⃗AB + (⃗AD −⃗AB )=(1− )⃗AB + ⃗AD =(2−t,t,2),
1 2 1 1 2 1 2 1
所以P(2−t,t,2)(0≤t≤2)
设面A BD的一个法向量为⃗n=(x ,y ,z ),
1 1 1 1
则¿
令x =1得y =1,z =1,∴⃗n=(1,1,1),
1 1 1
|⃗A P⋅⃗n| |t+2−t| 2√3
对于①:P到平面A BD的距离为d= 1 = = ,故①正确;
1 |⃗n| √3 3
学科网(北京)股份有限公司对于②:连接B C,D C,因为四边形BB D D为平行四边形,
1 1 1 1
∴BD//B D ,又BD⊂面A BD,B D ⊄面A BD,
1 1 1 1 1 1
∴B D //面A BD,
1 1 1
同理可证B C//面A BD,
1 1
又B D ∩B C=B ,所以面B D C//面A BD,
1 1 1 1 1 1 1
所以过点P且平行于面A BD的平面被正方体ABCD−A B C D 截得的多边形为△B D C,
1 1 1 1 1 1 1
√3
它是边长为2√2的等边三角形,故面积为 (2√2)
2=2√3,故②正确;
4
|⃗A P⋅⃗n|
√2
对于③:设直线PA 与面A BD所成角为θ,则sinθ=|cos⟨⃗A P,⃗n⟩|= 1 = ,
1 1 1 |⃗A P|⋅|⃗n| √3⋅√t2−2t+2
1
[√3 √6]
∵0≤t≤2,∴t2−2t+2∈[1,2],∴sinθ∈ , ,
3 3
[√3 √6]
所以直线PA 与面A BD所成角的正弦值的范围为 , ,故③正确;
1 1 3 3
对于④:当点P为B D 中点时P(1,1,2),设三棱锥P−A BD的外接球球心O(x ,y ,z ),
1 1 1 0 0 0
∵|OA |=|OB|=|OD|=|OP|,
1
∴x2+ y2+(z −2) 2=(x −2) 2+ y2+z2=x2+(y −2) 2+z2 =(x −1) 2+(y −1) 2+(z −2) 2 ,
0 0 0 0 0 0 0 0 0 0 0 0
1
解得x = y =z = ,
0 0 0 2
所以外接球半径R满足:R2=|OB|2= (1 −2 ) 2 + 1 + 1 = 11 ,
2 4 4 4
三棱锥P−A BD的外接球表面积为S=4πR2=11π,故④正确;
1
综上:①②③④均正确.
故选:D.
二.多选题(共4小题,满分20分,每小题5分)
9.(5分)(2023·高二单元测试)已知空间向量⃗m=(−1,2,5),⃗n=(2,−4,x),则下列选项中正确的是
( )
A.当⃗m⊥⃗n时,x=2 B.当⃗m//⃗n时,x=−10
学科网(北京)股份有限公司√10−2
C.当|⃗m+⃗n|=√5时,x=−4 D.当x=√10时,cos⟨⃗m,⃗n⟩=
6
【解题思路】对于A,利用空间向量垂直的坐标表示即可判断;对于B,利用空间向量平行的性质即可判
断;对于C,先根据空间向量运算法则计算出⃗m+⃗n,再利用模长公式列出方程,从而得以判断;对于D,
利用空间向量夹角余弦的坐标表示即可判断.
【解答过程】对于A,因为⃗m⊥⃗n,⃗m=(−1,2,5),⃗n=(2,−4,x),
所以⃗m·⃗n=(−1)×2+2×(−4)+5x=−10+5x=0,解得x=2,故A正确;
对于B,因为⃗m//⃗n,所以存在λ∈R,使得⃗m=λ⃗n,
则(−1,2,5)=λ(2,−4,x)=(2λ,−4λ,λx),即¿,解得¿,故B正确;
对于C,因为⃗m+⃗n=(−1+2,2−4,5+x)=(1,−2,5+x),
所以|⃗m+⃗n|=√12+(−2) 2+(5+x) 2=√5+(5+x) 2=√5,解得x=−5,故C错误;
对于D,因为x=√10,则⃗m=(−1,2,5),⃗n=(2,−4,√10),
⃗m·⃗n −1×2+2×(−4)+5×√10 √10−2
所以cos⟨⃗m,⃗,n⟩= = = ,故D正确.
|⃗m|·|⃗n| √1+4+25×√4+16+10 6
故选:ABD.
10.(5分)(2023·全国·高二专题练习)在自然界中,金刚石是天然存在的最硬的物质.如图1,这是组
成金刚石的碳原子在空间中排列的结构示意图,组成金刚石的每个碳原子都与其相邻的4个碳原子以完全
相同的方式连接.从立体几何的角度来看,可以认为4个碳原子分布在一个正四面体的四个顶点处,而中
间的那个碳原子处于与这4个碳原子距离都相等的位置,如图2所示.这就是说,图2中有AE=BE=CE
=DE,若正四面体ABCD的棱长为4,则( )
8√6
A.|⃗DE|= B.⃗EA+⃗EB+⃗EC+⃗ED=0⃗
9
C.⃗AE⋅⃗BC=0 D.⃗AC⋅⃗AE=8
【解题思路】由题意得E是正四面体ABCD外接球的球心.设点O是顶点A在底面的射影,取CD的中点
学科网(北京)股份有限公司G,AB的中点F,求得OB,AO,AE,由|⃗DE|=AE可判断A;求得EF=EG,结合⃗EA+⃗EB=2⃗EF,
√6
⃗EC+⃗ED=2⃗EG,可判断B;由AE⊥BC可判断C;求出cos〈⃗AC,⃗AE〉= ,进而求得⃗AC⋅⃗AE,可判
3
断D.
【解答过程】由题意得E是正四面体ABCD外接球的球心.
设点O是顶点A在底面的射影,则AO是正四面体ABCD的高,OB是△BCD的外接圆半径,
取CD的中点G,AB的中点F,连接BG,GF,则O在BG上,E在FG上,
2 2 √3 4√3 4√6
则OB= BG= × ×4= ,AO=√AB2−OB2= ,
3 3 2 3 3
因为BE2=(AO−AE) 2+BO2,即AE2=(AO−AE) 2+OB2,
2 2
则AE2= (4√6 −AE ) + (4√3) ,解得AE=√6.
3 3
对于A,|⃗DE|=AE=√6,故A错误;
√3
对于B,因为AG=BG= ×4=2√3,FG⊥AB,EG⊥CD,
2
所以EF=√AE2−AF2=√6−4=√2,EG=√DE2−DG2=√6−4=√2,
则EF=EG,又⃗EA+⃗EB=2⃗EF,⃗EC+⃗ED=2⃗EG,则⃗EA+⃗EB=−(⃗EC+⃗ED),
所以⃗EA+⃗EB+ ⃗EC+⃗ED=0⃗,故B正确;
对于C,因为AE⊥底面BCD,CD⊂底面BCD,所以AE⊥BC,所以⃗AE⋅⃗BC=0,故C正确;
AO √6
对于D,因为cos〈⃗AC,⃗AE〉=cos〈⃗AC,⃗AO〉= = ,
AC 3
√6
所以⃗AC⋅⃗AE=|⃗AC||⃗AE|cos⟨⃗AC,⃗AE⟩=4×√6× =8,故D正确.
3
故选:BCD.
学科网(北京)股份有限公司11.(5分)(2023·全国·高三专题练习)已知棱长为1的正方体ABCD−A B C D ,以正方体中心O为
1 1 1 1
球心的球O与正方体的各条棱相切,点P为球面上的动点,则下列说法正确的是( )
√2
A.球O在正方体外部分的体积为 π−1
3
[ 1 7]
B.若点P在球O的正方体外部(含正方体表面)运动,则⃗PA⋅⃗PB∈ − ,
4 4
2√2
C.若点P在平面ABCD下方,则直线AP与平面A B C D 所成角的正弦值最大为
1 1 1 1 3
1
D.若点P、M、N在球O的正方体外部(含正方体表面)运动,则⃗PM⋅⃗PN最小值为−
4
【解题思路】对于A,结合球的体积和正方体体积公式或利用球缺的体积公式即可判断;对于B,可取AB
中点E,可将⃗PA⋅⃗PB利用向量运算转化为⃗PA⋅⃗PB=(⃗PE+⃗EA)⋅(⃗PE+⃗EB)=(⃗PE) 2 −(⃗EA) 2 =|⃗PE| 2 − 1 ,
4
再结合|⃗PE|的范围即可判断;对于C,直线AP与平面A B C D 所成角最大时直线AP正好与平面ABCD
1 1 1 1
下方球O相切,根据几何关系即可求出所成角的最大正弦值,即可判断;对于D,可将⃗PM⋅⃗PN转化为
⃗PM⋅⃗PN=(⃗OM−⃗OP)⋅(⃗ON−⃗OP)=⃗OM⋅⃗ON−⃗OP⋅(⃗OM+⃗ON)+⃗OP2,再利用不等式进行转化求解,
即可判断.
√2
【解答过程】对于A,正方体的棱切球O的半径R= ,如下图所示,
2
3
4 (√2) √2
球O在正方体外部的体积V >V −V = π⋅ −1= π−1,
球O 正方体 3 2 3
或者可根据球O在平面A B C D 上方球缺部分的体积
1 1 1 1
学科网(北京)股份有限公司V = 1 π(3R−ℎ)⋅ℎ 2= 1 π⋅ [3√2 − (√2 − 1)] ⋅ (√2 − 1) 2 = (√2 − 5 ) π , ℎ 为球缺的高,
3 3 2 2 2 2 2 6 24
(√2 5 ) ( 5)
所以球O在正方体外部的体积为6V =6 − π= √2− π, A选项错误;
6 24 4
1
对于B,取AB中点E,可知E在球面上,可得⃗EB=−⃗EA= ⃗BA,所以
2
⃗PA⋅⃗PB=(⃗PE+⃗EA)⋅(⃗PE+⃗EB)=(⃗PE) 2 −(⃗EA) 2 =|⃗PE| 2 − 1 ,点P在球O的正方体外部(含正方体表
4
[ 1 7]
面)运动,所以0≤|⃗PE|≤√2(当PE为直径时,|⃗PE|=√2),所以⃗PA⋅⃗PB∈ − , ,B选项正确;
4 4
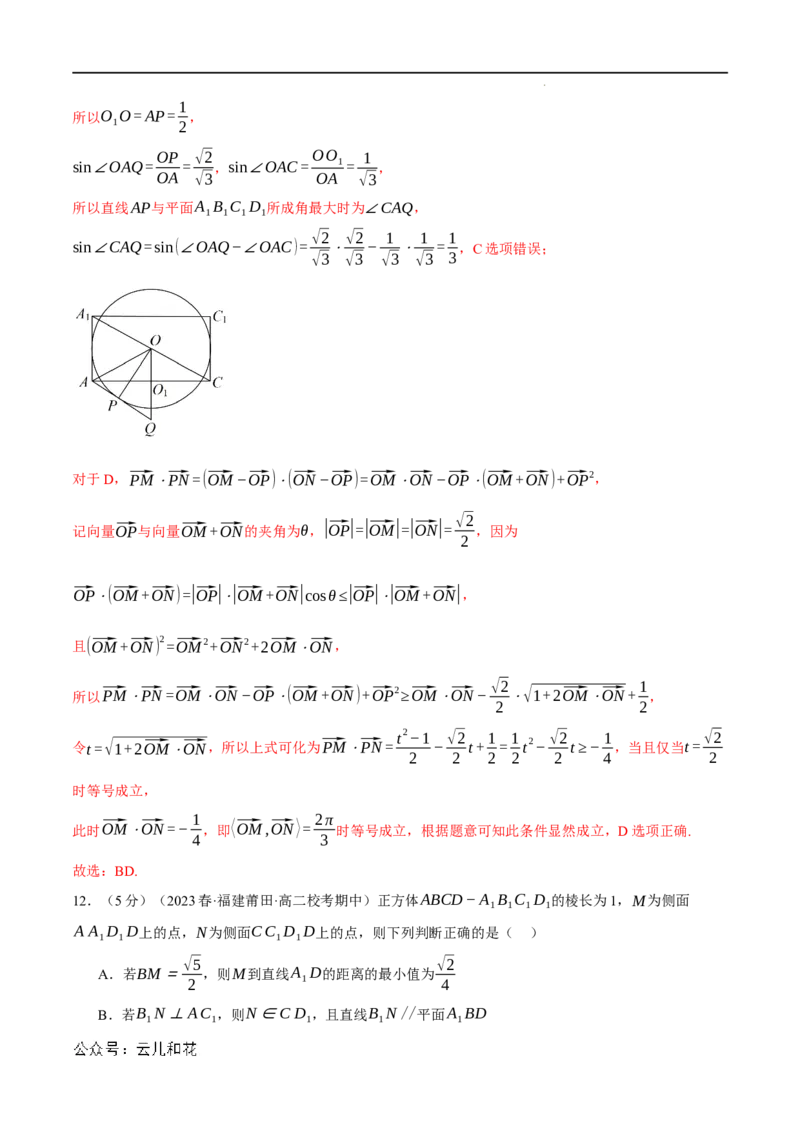
对于C,
若正方体上底面字母为ABCD,则直线AP与平面A B C D 所成角的正弦值最大时,如上图所示P点位
1 1 1 1
置,此时正弦值最大为1,
若正方体下底面字母为ABCD,设平面ABCD的中心为O ,直线AP与平面A B C D 所成角即为直线AP
1 1 1 1 1
与平面ABCD所成角,
则直线AP与平面A B C D 所成角最大时,直线AP正好与平面ABCD下方球O相切,过A作平面ABCD
1 1 1 1
√3
下方球O的切线,切点为P,将正方体及其棱切球的截面画出,如下图所示,可得OA= ,
2
√2 1
O A=OP= ,O O= ,∠OO A=∠APO=90∘,△APO≅△OO A,
1 2 1 2 1 1
学科网(北京)股份有限公司1
所以O O=AP= ,
1 2
OP √2 OO 1
sin∠OAQ= = ,sin∠OAC= 1= ,
OA √3 OA √3
所以直线AP与平面A B C D 所成角最大时为∠CAQ,
1 1 1 1
√2 √2 1 1 1
sin∠CAQ=sin(∠OAQ−∠OAC)= ⋅ − ⋅ = ,C选项错误;
√3 √3 √3 √3 3
对于D,⃗PM⋅⃗PN=(⃗OM−⃗OP)⋅(⃗ON−⃗OP)=⃗OM⋅⃗ON−⃗OP⋅(⃗OM+⃗ON)+⃗OP2,
√2
记向量⃗OP与向量⃗OM+⃗ON的夹角为θ,|⃗OP|=|⃗OM|=|⃗ON|= ,因为
2
⃗OP⋅(⃗OM+⃗ON)=|⃗OP|⋅|⃗OM+⃗ON|cosθ≤|⃗OP|⋅|⃗OM+⃗ON|,
且(⃗OM+⃗ON) 2 =⃗OM2+⃗ON2+2⃗OM⋅⃗ON,
√2 1
所以⃗PM⋅⃗PN=⃗OM⋅⃗ON−⃗OP⋅(⃗OM+⃗ON)+⃗OP2≥⃗OM⋅⃗ON− ⋅√1+2⃗OM⋅⃗ON+ ,
2 2
t2−1 √2 1 1 √2 1 √2
令t=√1+2⃗OM⋅⃗ON,所以上式可化为⃗PM⋅⃗PN= − t+ = t2− t≥− ,当且仅当t=
2 2 2 2 2 4 2
时等号成立,
1 2π
此时⃗OM⋅⃗ON=− ,即 ⟨⃗OM,⃗ON⟩= 时等号成立,根据题意可知此条件显然成立,D选项正确.
4 3
故选:BD.
12.(5分)(2023春·福建莆田·高二校考期中)正方体ABCD−A B C D 的棱长为1,M为侧面
1 1 1 1
A A D D上的点,N为侧面CC D D上的点,则下列判断正确的是( )
1 1 1 1
√5 √2
A.若BM= ,则M到直线A D的距离的最小值为
2 1 4
B.若B N⊥AC ,则N∈CD ,且直线B N//平面A BD
1 1 1 1 1
学科网(北京)股份有限公司√3
C.若M∈A D,则B M与平面A BD所成角正弦的最小值为
1 1 1 3
√3
D.若M∈A D,N∈CD ,则M,N两点之间距离的最小值为
1 1 3
1
【解题思路】由已知可推得M为以A点为圆心, 为半径的圆上.作图,即可根据圆的性质得出最小值,判
2
断A项;先证明AC ⊥平面A BD,结合B N⊥AC ,即可得出B N//平面A BD;建立空间直角坐
1 1 1 1 1 1
1
标系,求出平面A BD的法向量,表示出cos⟨⃗n ,⃗B M⟩ = ,根据不等式的性质,即可
1 1 1 √3√2λ2−4λ+3
判断C项;MN为直线DA 与CD 的公垂线段时,MN最小.设⃗n =(x ,y ,z ),且⃗n ⊥⃗D A ,
1 1 2 2 2 2 2 1
⃗n ⊥⃗CD ,求出⃗n ,即可根据投影向量,求出最小值.
2 1 2
√5 √5
【解答过程】对于A项,因为BM= ,所以M在以B为球心, 为半径的球上.
2 2
又M为侧面A A D D上的点,所以M在球被平面A A D D截得的交线上.
1 1 1 1
√5 1
因为,AB⊥平面A A D D,AB=1,BM= ,所以AM=√BM2−AB2= ,
1 1 2 2
1
所以,M为以A点为圆心, 为半径的圆上.
2
√2 √2 1
如图1,AM ⊥A D,则AM = ,M到直线A D的距离的最小值为 − ,故A项错误;
1 1 1 2 1 2 2
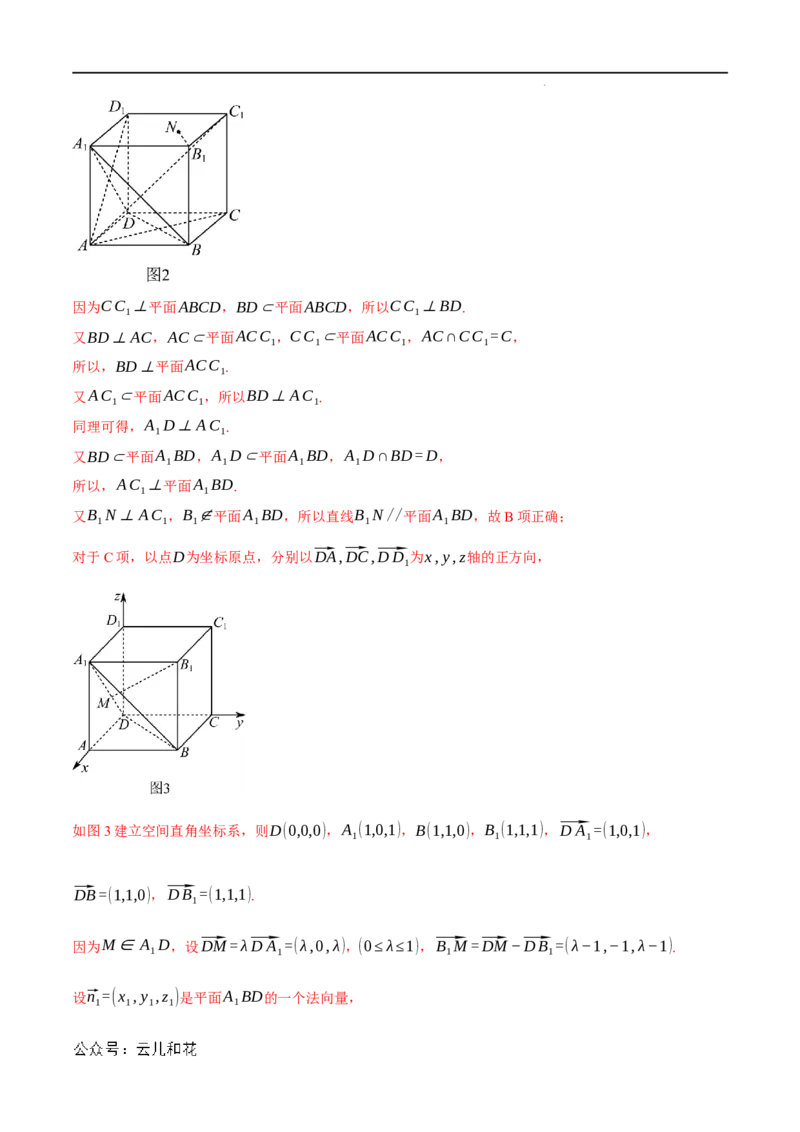
对于B项,如图2,连结AC,AD .
1
学科网(北京)股份有限公司因为CC ⊥平面ABCD,BD⊂平面ABCD,所以CC ⊥BD.
1 1
又BD⊥AC,AC⊂平面ACC ,CC ⊂平面ACC ,AC∩CC =C,
1 1 1 1
所以,BD⊥平面ACC .
1
又AC ⊂平面ACC ,所以BD⊥AC .
1 1 1
同理可得,A D⊥AC .
1 1
又BD⊂平面A BD,A D⊂平面A BD,A D∩BD=D,
1 1 1 1
所以,AC ⊥平面A BD.
1 1
又B N⊥AC ,B ∉平面A BD,所以直线B N//平面A BD,故B项正确;
1 1 1 1 1 1
对于C项,以点D为坐标原点,分别以⃗DA,⃗DC,⃗DD 为x,y,z轴的正方向,
1
如图3建立空间直角坐标系,则D(0,0,0),A (1,0,1),B(1,1,0),B (1,1,1),⃗DA =(1,0,1),
1 1 1
⃗DB=(1,1,0),⃗DB =(1,1,1).
1
因为M∈A D,设⃗DM=λ⃗DA =(λ,0,λ),(0≤λ≤1),⃗B M=⃗DM−⃗DB =(λ−1,−1,λ−1).
1 1 1 1
设⃗n =(x ,y ,z )是平面A BD的一个法向量,
1 1 1 1 1
学科网(北京)股份有限公司则¿,即¿,
取x =1,则y =z =−1,⃗n =(1,−1,−1)是平面A BD的一个法向量.
1 1 1 1 1
⃗n ⋅⃗B M λ−1+1−(λ−1) 1
则cos⟨⃗n ,⃗B M⟩= 1 1 = =
,
1 1 |⃗n||⃗B M| √3√(λ−1) 2+1+(λ−1) 2 √3√2λ2−4λ+3
1 1
又2λ2−4λ+3=2(λ−1) 2+1≥1,当λ=1时,有最小值1,
1 1 √3 √3
所以, ≤ = ,即cos⟨⃗n ,⃗B M⟩≤ ,
√3√2λ2−4λ+3 √3 3 1 1 3
√3
所以,B M与平面A BD所成角正弦的最大值为 ,故C项错误;
1 1 3
对于D项,由C项知,⃗DA =(1,0,1),⃗CD =(0,−1,1).
1 1
当MN⊥DA ,MN⊥CD ,即MN为直线DA 与CD 的公垂线段时,MN最小.
1 1 1 1
设⃗n =(x ,y ,z ),且⃗n ⊥⃗DA ,⃗n ⊥⃗CD ,
2 2 2 2 2 1 2 1
则¿,即¿,
取x =1,则⃗n =(1,−1,−1).
2 2
|⃗DC⋅⃗n | 1 √3
⃗DC在⃗n 方向上的投影向量的模为 2 = = ,
2 |⃗n | √3 3
2
√3
所以,M,N两点之间距离的最小值为d= ,故D项正确.
3
故选:BD.
三.填空题(共4小题,满分20分,每小题5分)
13.(5分)(2023秋·重庆长寿·高二统考期末)已知空间三点坐标分别为A(1,1,1),B(0,3,0),
学科网(北京)股份有限公司11
C(−2,−1,4),点P(−3,x,1)在平面ABC内,则实数x的值为 .
3
【解题思路】根据题意,存在实数λ,μ使得等式⃗AP=λ⃗AB+μ⃗AC成立,将各点坐标代入,列出方程组求解即
可.
【解答过程】∵点P(−3,x,1)在平面ABC内,
∴存在实数λ,μ使得等式⃗AP=λ⃗AB+μ⃗AC成立,
∴(−4,x−1,0)=λ(−1,2,−1)+μ(−3,−2,3),
∴¿,解得¿.
11
故答案为: .
3
√10
14.(5分)(2023春·高二课时练习)已知向量⃗a=(1,1,0),⃗b=(m,0,2),cos⟨⃗a,⃗b⟩=− ,若向量
10
⃗a+k⃗b与2⃗a+⃗b所成角为钝角,则实数k的范围是 k<−1 .
⃗a⋅⃗b
【解题思路】根据cos⟨⃗a,⃗b⟩= 求出m的值,再求出⃗a+k⃗b与2⃗a+⃗b的坐标,依题意可得
|⃗a|⋅ |⃗b|
(⃗a+k⃗b)⋅(2⃗a+⃗b)<0,根据数量积的坐标表示得到不等式求出参数的取值范围,再检验两向量共线的情况.
√10
【解答过程】解:因为⃗a=(1,1,0),⃗b=(m,0,2),cos⟨⃗a,⃗b⟩=− ,
10
⃗a⋅⃗b m √10
所以cos⟨⃗a,⃗b⟩= = =− ,解得m=−1,
|⃗a|⋅ |⃗b| √2×√m2+4 10
所以⃗b=(−1,0,2),
所以⃗a+k⃗b=(1−k,1,2k),2⃗a+⃗b=(1,2,2),
因为向量⃗a+k⃗b与2⃗a+⃗b所成角为钝角,
所以(⃗a+k⃗b)⋅(2⃗a+⃗b)=1−k+2+4k<0,解得k<−1,
1−k 1 2k 1
若向量⃗a+k⃗b与2⃗a+⃗b共线,则 = = ,解得k= ,
1 2 2 2
1
此时⃗a+ ⃗b与2⃗a+⃗b共线同向,
2
综上可得k<−1.
学科网(北京)股份有限公司故答案为:k<−1.
15.(5分)(2023春·江苏常州·高二校联考期中)一种糖果的包装纸由一个边长为6的正方形和2个等腰
直角三角形组成(如图1),沿AD,BC将2个三角形折起到与平面ABCD垂直(如图2),连接EF,
AE,CF,AC,若点P满足⃗DP=x⃗DA+ y⃗DC+z⃗DF且x+ y+z=1,则|⃗EP|的最小值为 4√3 .
【解题思路】由向量⃗DP满足条件可知P是平面ACF上的动点,转化为求E到平面ACF的距离,利用补形
及等体积法求解即可.
【解答过程】因为点P满足⃗DP=x⃗DA+ y⃗DC+z⃗DF且x+ y+z=1,
所以A,C,F,P四点共面,即P是平面ACF上的动点,
所以|⃗EP|的最小值即为E到平面ACF的距离.
由题意,几何体可补成边长为6的正方体,如图,
则可知AF=AC=CF=AE=FE=CE=6√2,
设E到平面ACF的距离为
ℎ
,
1
则V = ⋅S ⋅ℎ =V −4V ,
E−ACF 3 △ACF 正方体 E−ABC
1 √3 1 1
即 × ×(6√2) 2 ⋅ℎ =63−4× × ×6×6×6,
3 4 3 2
解得
ℎ
=4√3,
所以|⃗EP|的最小值为4√3.
学科网(北京)股份有限公司故答案为:4√3.
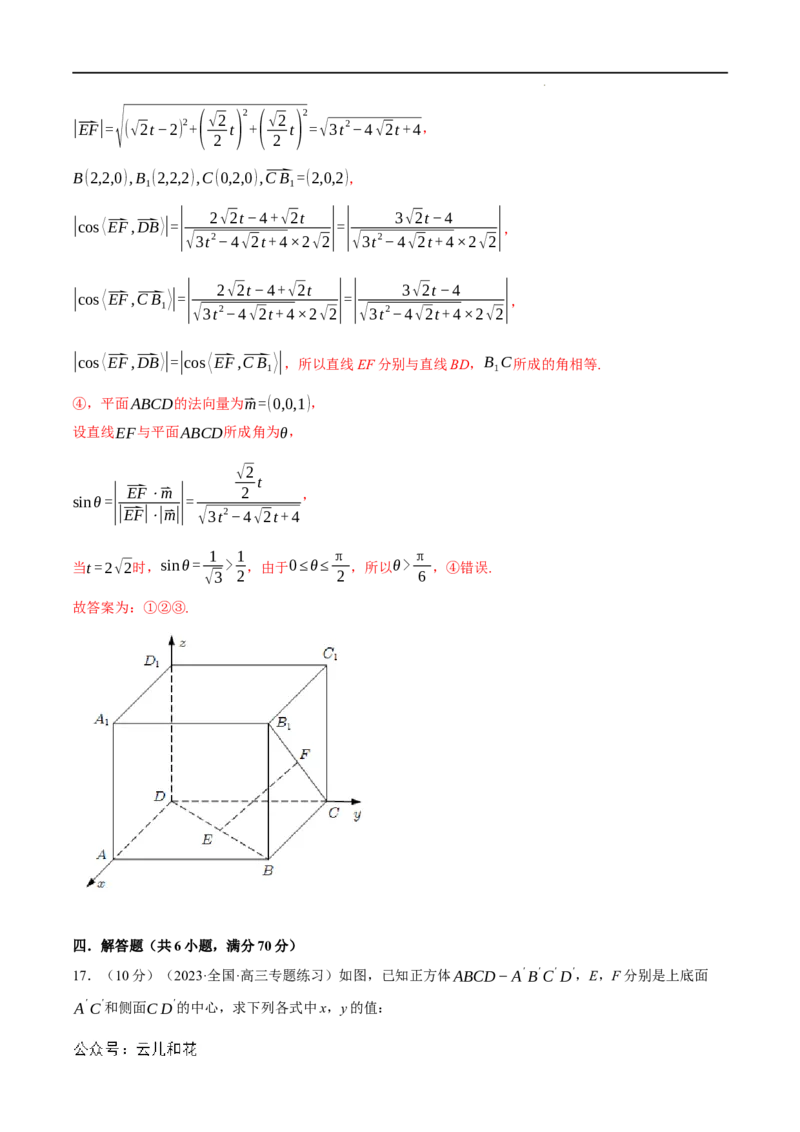
16.(5分)(2022·贵州贵阳·统考一模)如图,在正方体ABCD−A B C D 中,点E在BD上,点F在
1 1 1 1
B C上,且BE=CF.则下列四个命题中所有真命题的序号是 ①②③ .
1
①当点E是BD中点时,直线EF//平面DCC D ;
1 1
②当DE=2EB时,EF⊥BD;
③直线EF分别与直线BD,B C所成的角相等;
1
π
④直线EF与平面ABCD所成的角最大为 .
6
【解题思路】建立空间直角坐标系,利用向量法对四个命题逐一分析,从而确定其中的真命题.
【解答过程】设正方体的边长为2,建立如图所示空间直角坐标系,
设BE=CF=t,0≤t≤2√2,
①,当E是BD的中点时,F是B C的中点,
1
E(1,1,0),F(1,2,1),⃑EF=(0,1,1),
平面DCC D 的一个法向量为⃑n =(1,0,0),⃑n⋅⃑EF=0,
1 1 1
由于EF⊂平面DCC D ,所以EF//平面DCC D ,①为真命题.
1 1 1 1
1 1
②,当DE=2EB时,BE= BE,CF= CB ,
3 3 1
(4 4 ) (2 2) ( 2 2 2)
E , ,0 ,F ,2, ,⃑EF= − , , ,B(2,2,0),
3 3 3 3 3 3 3
⃑EF⋅⃑DB=0,所以EF⊥BD,所以②正确.
( √2 √2 ) ( √2 √2 )
③,E (2√2−t)× ,(2√2−t)× ,0 = 2− t,2− t,0 ,
2 2 2 2
(√2 √2 ) ( √2 √2 )
F t,2, t ,⃑EF= √2t−2, t, t ,
2 2 2 2
学科网(北京)股份有限公司|⃑EF|= √ (√2t−2) 2+ (√2 t ) 2 + (√2 t ) 2 =√3t2−4√2t+4,
2 2
B(2,2,0),B (2,2,2),C(0,2,0),⃑CB =(2,0,2),
1 1
| 2√2t−4+√2t | | 3√2t−4 |
|cos⟨⃑EF,⃑DB⟩|= =
,
√3t2−4√2t+4×2√2 √3t2−4√2t+4×2√2
| 2√2t−4+√2t | | 3√2t−4 |
|cos⟨⃑EF,⃑CB ⟩|= =
,
1 √3t2−4√2t+4×2√2 √3t2−4√2t+4×2√2
|cos⟨⃑EF,⃑DB⟩|=|cos⟨⃑EF,⃑CB ⟩|,所以直线EF分别与直线BD,B C所成的角相等.
1 1
④,平面ABCD的法向量为⃑m=(0,0,1),
设直线EF与平面ABCD所成角为θ,
√2
t
| ⃑EF⋅⃑m | 2 ,
sinθ= =
|⃑EF|⋅|⃑m| √3t2−4√2t+4
1 1 π π
当t=2√2时,sinθ= > ,由于0≤θ≤ ,所以θ> ,④错误.
√3 2 2 6
故答案为:①②③.
四.解答题(共6小题,满分70分)
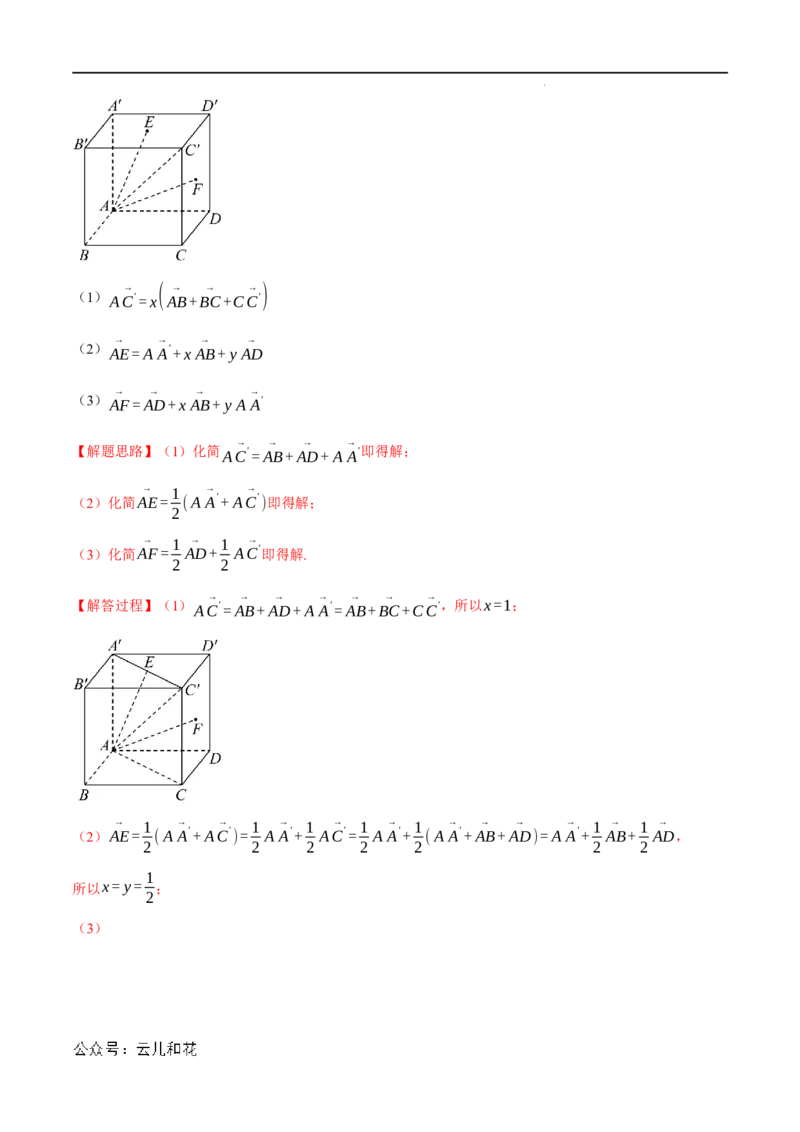
17.(10分)(2023·全国·高三专题练习)如图,已知正方体ABCD−A′B′C′D′,E,F分别是上底面
A′C′和侧面CD′的中心,求下列各式中x,y的值:
学科网(北京)股份有限公司(1) AC → ′=x ( A → B+B → C+CC → ′ )
→ → → →
(2) AE=A A′+x AB+ y AD
→ → → →
(3) AF=AD+x AB+ y A A′
→ → → →
【解题思路】(1)化简 AC′=AB+AD+A A′即得解;
→ 1 → →
(2)化简AE= (A A′+AC′ )即得解;
2
→ 1 → 1 →
(3)化简AF= AD+ AC′即得解.
2 2
→ → → → → → →
【解答过程】(1) AC′=AB+AD+A A′=AB+BC+CC′,所以x=1;
→ 1 → → 1 → 1 → 1 → 1 → → → → 1 → 1 →
(2)AE= (A A′+AC′ )= A A′+ AC′= A A′+ (A A′+AB+AD)=A A′+ AB+ AD,
2 2 2 2 2 2 2
1
所以x= y= ;
2
(3)
学科网(北京)股份有限公司→ 1 → 1 → 1 → 1 → → → → 1 → 1 →
AF= AD+ AC′= AD+ (AB+A A′+AD)=AD+ AB+ A A′ ,
2 2 2 2 2 2
1
所以x= y=
.
2
18.(12分)(2023春·四川成都·高二校联考期中)已知空间向量⃗a=(1,0,1),⃗b=(2,−1,0),
⃗c=(λ+4,−λ,λ).
(1)若(⃗a+⃗b) //⃗c,求λ;
(2)若k⃗a+⃗b与2⃗a−⃗b相互垂直,求k.
【解题思路】(1)根据空间向量共线公式列式求参即可;
(2)根据空间向量垂直数量积为0列式求参即可.
【解答过程】(1)∵⃗a+⃗b=(3,−1,1),(⃗a+⃗b)//⃗c
∴(⃗a+⃗b)=μ⃗c,μ∈R,
即3=μ(λ+4),且−1=−μλ,1=μλ,解得λ=2;
(2)∵k⃗a+⃗b=(k+2,−1,k),2⃗a−⃗b=(0,1,2),
1
又∵(k⃗a+⃗b)⋅(2⃗a−⃗b)=2k−1=0,解得k= .
2
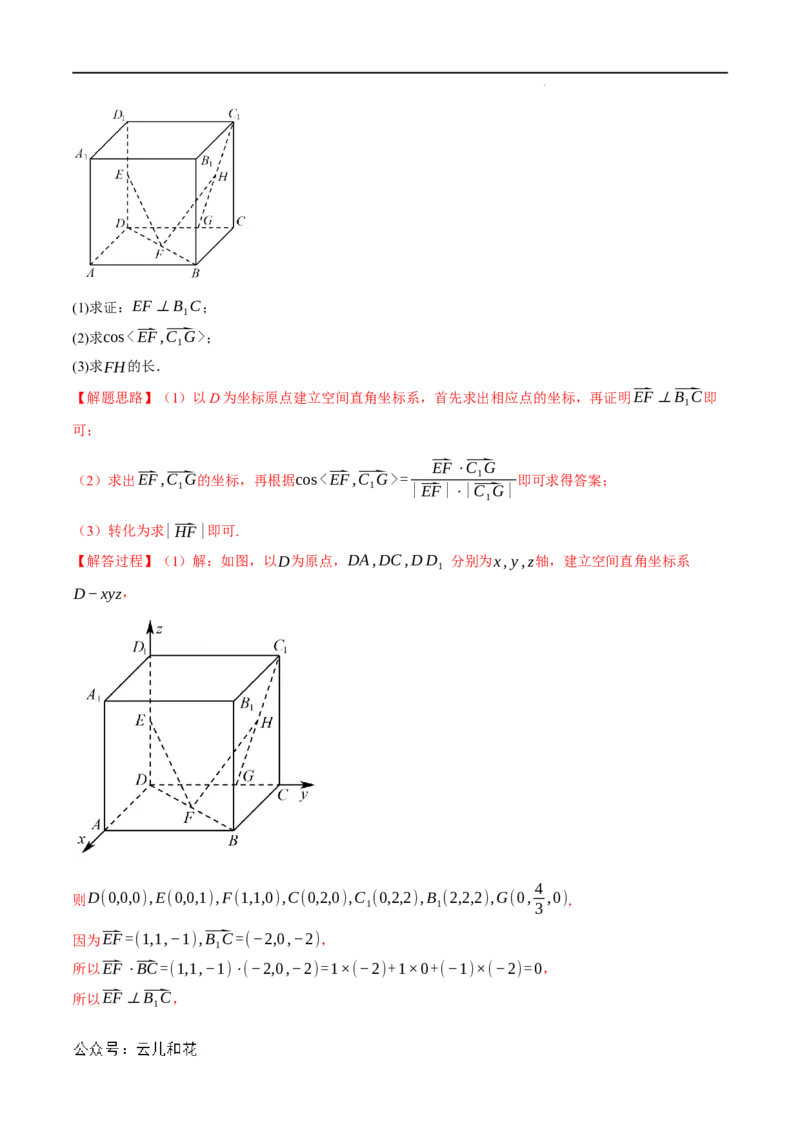
19.(12分)(2023·江苏·高二专题练习)棱长为2的正方体中,E、F分别是DD 、DB的中点,G在棱
1
1
CD上,且CG= CD,H是C G的中点.建立适当的空间直角坐标系,解决下列问题:
3 1
学科网(北京)股份有限公司(1)求证:EF⊥B C;
1
(2)求cos<⃑EF,⃑C G>;
1
(3)求FH的长.
【解题思路】(1)以D为坐标原点建立空间直角坐标系,首先求出相应点的坐标,再证明⃑EF⊥⃑B C即
1
可;
⃑EF⋅⃑C G
(2)求出⃑EF,⃑C G的坐标,再根据cos<⃑EF,⃑C G>= 1 即可求得答案;
1 1 |⃑EF|⋅|⃑C G|
1
(3)转化为求|⃑HF|即可.
【解答过程】(1)解:如图,以D为原点,DA,DC,DD 分别为x,y,z轴,建立空间直角坐标系
1
D−xyz,
4
则D(0,0,0),E(0,0,1),F(1,1,0),C(0,2,0),C (0,2,2),B (2,2,2),G(0, ,0),
1 1 3
因为⃑EF=(1,1,−1),⃑B C=(−2,0,−2),
1
所以⃑EF⋅⃑BC=(1,1,−1)⋅(−2,0,−2)=1×(−2)+1×0+(−1)×(−2)=0,
所以⃑EF⊥⃑B C,
1
学科网(北京)股份有限公司故EF⊥B C;
1
2 2√10
(2)解:因为⃑C G=(0,− ,−2),所以|⃑C G|=
1 3 1 3
2 2 4
因为|⃑EF|=√3,且⃑EF⋅⃑C G=(1,1,−1)⋅(0,− ,−2)=2− = ,
1 3 3 3
4
⃑EF⋅⃑C G 3 4 3 2 √30
所以cos<⃑EF,⃑C G>= 1 = = ⋅ = = ;
1 |⃑EF||⃑C G| 2√10 3 2√30 √30 15
1 √3⋅
3
5
(3)解:因为H是C G的中点,所以H(0, ,1)
1 3
又因为F(1,1,0),
2
所以⃑HF=(1,− ,−1),
3
√ 2 2 √22 √22
|⃑FH|= 12+(− ) +(−1) 2= = .
3 9 3
√22
即FH= .
3
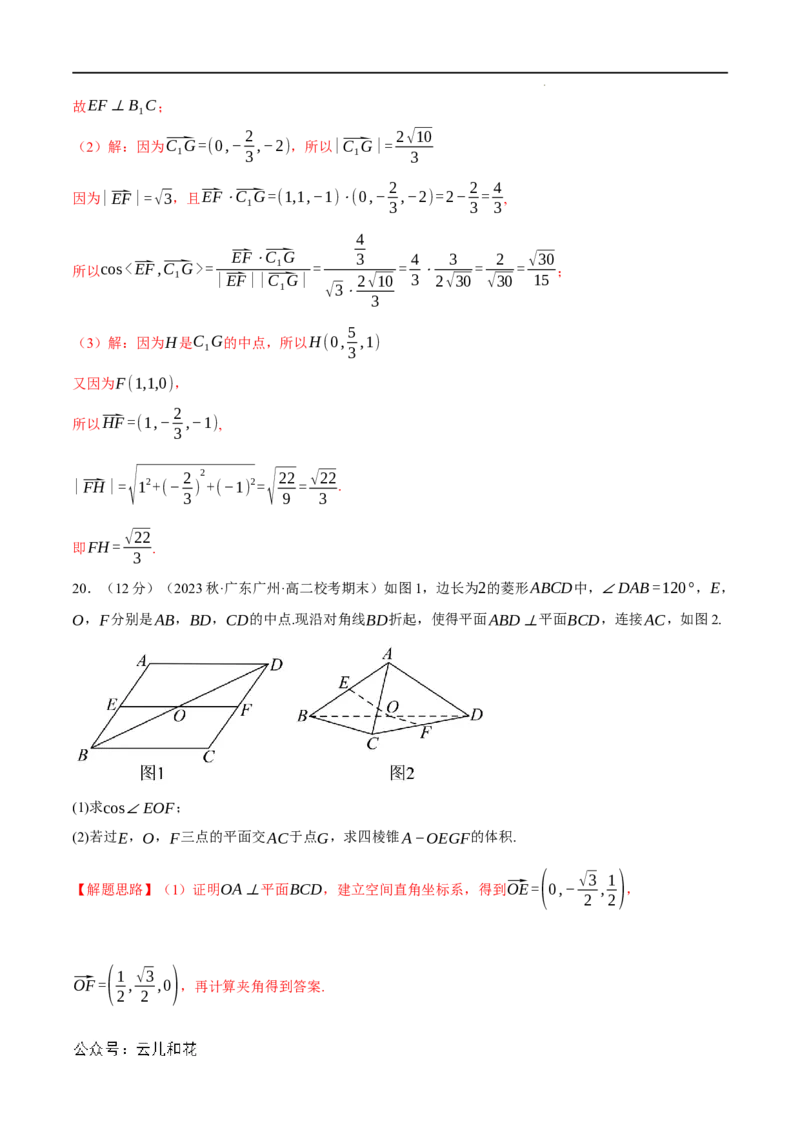
20.(12分)(2023秋·广东广州·高二校考期末)如图1,边长为2的菱形ABCD中,∠DAB=120°,E,
O,F分别是AB,BD,CD的中点.现沿对角线BD折起,使得平面ABD⊥平面BCD,连接AC,如图2.
(1)求cos∠EOF;
(2)若过E,O,F三点的平面交AC于点G,求四棱锥A−OEGF的体积.
( √3 1)
【解题思路】(1)证明OA⊥平面BCD,建立空间直角坐标系,得到⃗OE= 0,− , ,
2 2
(1 √3 )
⃗OF= , ,0 ,再计算夹角得到答案.
2 2
学科网(北京)股份有限公司√21
(2)计算平面OEGF的法向量为⃗n=(−3,√3,3),再计算A到平面OEGF的距离为ℎ = ,最后计算体
7
积得到答案.
【解答过程】(1)连接OA,OC,平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,
OA⊥BD,OA⊂平面ABD,故OA⊥平面BCD,
分别以OC,OD,OA所在直线为x,y,z轴建立空间直角坐标系,
则A(0,0,1),B(0,−√3,0),C(1,0,0),D(0,√3,0),
( √3 1) (1 √3 )
因为E,F分别是AB,CD的中点,所以⃗OE= 0,− , ,⃗OF= , ,0 ,
2 2 2 2
3
−
所以 cos∠EOF= ⃗OE⋅⃗OF = 4 =− 3 .
|⃗OE|⋅|⃗OF| 1×1 4
(2)连接EG,FG,AF,
设平面OEGF的法向量为⃗n=(x,y,z),则⃗n⋅⃗OE=0,⃗n⋅⃗OF=0,
即¿,令y =√3,则x =−3,z =3,所以⃗n=(−3,√3,3),
1 1 1
( √3 1) |⃗AE⋅⃗n| 3 √21
设A到平面OEGF的距离为ℎ,而⃗AE= 0,− ,− ,ℎ = = = ,
2 2 |⃗n| √21 7
√ 9 √7
依题意得四边形OEGF是一个菱形,∠EOF∈(0,π),sin∠EOF= 1− = ,
16 4
√7
所以S =2S =OE⋅OF⋅sin∠EOF= ,
四边形OEGF △OEF 4
1 1 √7 √21 √3
所以V = ×S ×ℎ = × × = .
A−OEGF 3 四边形OEGF 3 4 7 12
学科网(北京)股份有限公司21.(12分)(2023春·江苏扬州·高二统考期中)如图,在三棱柱ABC−A B C 中,底面是边长为2的
1 1 1
等边三角形,CC =2,D,E分别是线段AC,CC 的中点,C 在平面ABC内的射影为D.
1 1 1
(1)求证:A C⊥平面BDE;
1
(2)若点F为棱B C 的中点,求点F到平面BDE的距离;
1 1
(3)若点F为线段B C 上的动点(不包括端点),求锐二面角F−BD−E的余弦值的取值范围.
1 1
【解题思路】(1)法一:利用线面垂直、面面垂直的性质定理与判定定理可证;
法二:建立空间直角坐标系,利用数量积为0,可证BD⊥A C,DE⊥A C,从而得证;
1 1
法三:如法二建立空间直角坐标系,求出平面BDE的一个法向量,证明其与A C平行,从而得证;
1
(2)利用空间向量法求点到面的距离;
(3)利用空间向量求出二面角的余弦值,再借助函数性质求值域.
【解答过程】(1)法一:连结AC ,因为△ABC为等边三角形,D为AC中点,∴BD⊥AC,
1
又C D⊥平面ABC,BD⊂平面ABC,∴C D⊥BD
1 1
∵AC∩C D=D,AC,C D⊂平面A A C C
1 1 1 1
∴BD⊥平面A A C C,又A C⊂平面A A C C,∴BD⊥A C,
1 1 1 1 1 1
由题设知四边形A A C C为菱形,∴A C⊥AC ,
1 1 1 1
∵D,E分别为AC,CC 中点,∴DE∥AC ,∴A C⊥DE,
1 1 1
又BD∩DE=D, BD∩DE=D,BD,DE⊂平面BDE,∴A C⊥平面BDE.
1
法二:由C D⊥平面ABC,BD,AC⊂平面ABC,∴C D⊥BD,C D⊥AC,
1 1 1
又△ABC为等边三角形,D为AC中点,∴BD⊥AC,则以D为坐标原点,⃗DB,⃗DA,⃗DC 所在直线为
1
x,y,z轴,可建立如图所示空间直角坐标系,则
( 1 √3)
D(0,0,0),B(√3,0,0),C(0,−1,0),C (0,0,√3),E 0,− , ,B (√3,1√3),A (0,2,√3),
1 2 2 1 1
学科网(北京)股份有限公司( 1 √3)
∴⃗DB=(√3,0,0),⃗DE= 0,− , , ⃗A C=(0,−3,−√3)
2 2 1
∵⃗DB·⃗A C=0,⃗DE·⃗A C=0 ∴ BD⊥A C,DE⊥A C
1 1 1 1
又BD∩DE=D, BD∩DE=D,BD,DE⊂平面BDE,∴A C⊥平面BDE.
1
法三:(同法二建系)设平面BDE的一个法向量为⃗m=(x,y,z)
∵ ¿,即¿
不妨取z=1,则y=√3,则⃗m=(0,√3,1)
所以平面BDE的一个法向量为⃗m=(0,√3,1)
∵ ⃗A C=(0,−3,−√3),∴⃗A C=−√3⃗m,∴⃗A C//⃗m,∴ A C⊥平面BDE
1 1 1 1
(√3 1 )
(2)由(1)坐标法得F , ,√3 ,平面BDE的一个法向量为⃗m=(0,√3,1)(或⃗m=⃗CA =(0,3,√3)
2 2 1
(√3 1 )
)∵⃗DF= , ,√3
2 2
√3
+√3
∴点到F到平面BDE的距离= |⃗m⋅⃗DF| 2 3√3
= =
|⃗m| 2 4
(3)⃗C B =(√3,1,0),⃗C A =(0,3,√3)
1 1 1
设F(x,y,z),⃗C F=λ⃗C B (0<λ<1),则(x,y,z−√3)=(√3λ,λ,0),
1 1 1
学科网(北京)股份有限公司∴x=√3λ,y=λ,z=√3,∴F(√3λ,λ,√3),∴⃗DF=(√3λ,λ,√3);
由(1)知:A C⊥平面BDE,∴平面BDE的一个法向量⃗m=⃗CA =(0,3,√3)
1 1
(或者由(1)中待定系数法求出法向量);
设平面FBD的法向量⃗n=(a,b,c),
则¿,令b=√3,则a=0,c=−λ,∴⃗n=(0,√3,−λ);
|⃗m⋅⃗n| |3√3−√3λ| |3−λ| 1√(3−λ) 2
∴|cos⟨⃗m,⃗n⟩|= = = = ,
|⃗m|⋅|⃗n| 2√3×√3+λ2 2√3+λ2 2 3+λ2
1√ t2 1√ 1
∴|cos⟨⃗m,⃗n⟩|= =
令3−λ=t∈(2,3),则λ=3−t 2 12−6t+t2 2 12 6 ;
− +1
t2 t
1 (1 1) 12 6 (1 ) (1 √3)
∵ ∈ , ,∴ − +1∈ ,1 ,∴|cos⟨⃗m,⃗n⟩|∈ , ,
t 3 2 t2 t 3 2 2
(1 √3)
即锐二面角F−BD−E的余弦值的取值范围为 , .
2 2
22.(12分)(2023·天津和平·统考三模)如图,四棱台ABCD−A B C D 中,上、下底面均是正方形,
1 1 1 1
且侧面是全等的等腰梯形,AB=2A B =4,E、F分别为DC、BC的中点,上下底面中心的连线O O垂直
1 1 1
于上下底面,且O O与侧棱所在直线所成的角为45∘.
1
(1)求证:BD ∥平面C EF;
1 1
(2)求点A 到平面C EF的距离;
1 1
3√22
(3)边BC上是否存在点M,使得直线A M与平面C EF所成的角的正弦值为 ,若存在,求出线段
1 1 22
BM的长;若不存在,请说明理由.
【解题思路】(1)建立空间直角坐标系后,用直线的方向向量和平面的法向量垂直即可证明线面平行;
学科网(北京)股份有限公司(2)建立空间直角坐标系后,用点到平面的距离公式即可求解;(3)假设存在,列出方程求解即可.
【解答过程】(1)
因为OO ⊥平面ABCD,以点O为坐标原点,⃗DA,⃗OF,⃗OO 的方向分别为x轴,y轴,z轴的正方向,建
1 1
立如图所示的空间直角坐标系.
因为侧棱所在直线与上下底面中心的连线OO 所成的角为45°,则
1
B(2,2,0),D (−1,−1,√2),C (−1,1,√2),F(0,2,0),E(−2,0,0),A (1,−1,√2)
1 1 1
所以⃗BD =(−3,−3,√2),⃗CE =(−1,−1,√2),⃗EF=(2,2,0)
1 1
设平面C EF的一个法向量为⃗n=(x,y,z),则
1
¿,令x=1,则⃗n=(1,−1,0).
因为⃗BD =(−3,−3,√2),所以⃗n⋅⃗BD =0,所以⃗n⊥⃗BD ,
1 1 1
又因为BD ⊄平面C EF,所以BD ∥平面C EF.
1 1 1 1
(2)由(1)知,⃗A E=(−3,1,−√2),
1
|⃗A E⋅⃗n| |−4|
所以点A 到平面C EF的距离为d= 1 = =2√2.
1 1
|⃗n| √2
(3)假设边BC上存在点M(x,2,0)满足条件,x∈[−2,2],
则⃗A M=(x−1,3,−√2),
1
设直线A M与平面C EF所成角为θ,
1 1
|⃗A M⋅⃗n|
|x−4| 3√22
由题意可得sinθ=|cos<⃗A M,⃗n>|= 1 = =
,
1 ⃗
|A M|⋅|⃗n|
√2√x2−2x+12 22
1
化简得x2−35x+34=0,则x=1或x=34(舍去),
即存在点M符合题意,此时BM=1.
学科网(北京)股份有限公司学科网(北京)股份有限公司