文档内容
2024 届高三级 11 月四校联考 数学 试题
佛山市第一中学、广州市第六中学
汕头市金山中学、中山市第一中学
试卷总分: 分 考试时间: 分钟
注意事项:
答卷前,考生务必将自己的姓名15、0准考证号填写在答题1卡20上。本次考试采用特殊编排
考号,请考生正确填涂。
1. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如
需改动用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡
2. 上。写在本试卷上无效。
第一部分 选择题
(共60分)
一、单选题(本大题共8小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1.已知集合 , ,则A∩B= ( )
A. A B. B C. ∁ A D. ∁ B
R R
2.已知向量 , ,若 ,则m的值为( )
A. −6 B. −4 C. 0 D. 6
{ ax−3,x≥4,
3.若函数f (x)= (a>0,a≠1)是R上的单调函数,则a的取值范围为( )
−ax+4,x<4
( 5] ( 5] ( 4] [4 )
A. (0,1)∪ 1, B. 1, C. 0, D. ,1
4 4 5 5
4.若复数z满足(1+i)z=|1+i|,则 z 的虚部为( )
√2 √2 √2
A. −√2i B. − C. i D.
2 2 2
5.数列{a }满足a =2019,且对∀n∈N∗恒有a =a +2n ,则a =( )
n 1 n+3 n 7
A. 2037 B. 2035 C. 2023 D. 2021
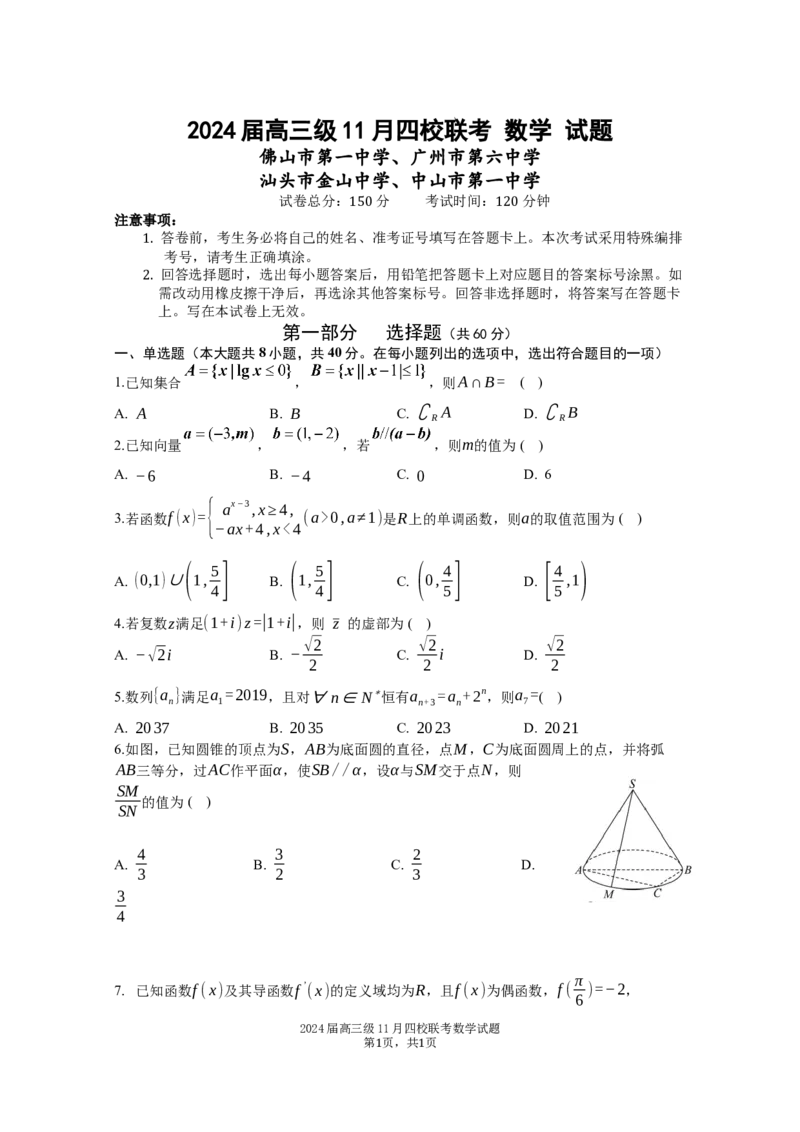
6.如图,已知圆锥的顶点为S,AB为底面圆的直径,点M,C为底面圆周上的点,并将弧
AB三等分,过AC作平面α,使SB//α,设α与SM交于点N,则
SM
的值为( )
SN
4 3 2
A. B. C. D.
3 2 3
3
4
π
7. 已知函数f(x)及其导函数f’ (x)的定义域均为R,且f(x)为偶函数,f( )=−2,
6
2024届高三级11月四校联考数学试题
第 页,共 页
1 1π 1
且3f(x)cosx+f’ (x)sinx>0,则不等式f(x+ )cos3x− >0的解集为( )
2 4
π π 2π π 2π
A. (− ,+∞) B.( ,+∞) C. (− , ) D. (− ,+∞)
3 3 3 3 3
8.已知函数f(x)=√3sin2
ωx
+
1
sinωx−
√3
(ω>0),若f(x)在
(π
,
3π)
上无零点,则ω
2 2 2 2 2
的取值范围是( )
2 8 2 8 2 2 8
A. (0, ]∪[ ,+∞) B.(0, ]∪[ ,1] C. (0, ]∪[ , ] D.
9 9 9 9 9 3 9
2 8
( , ]∪[1,+∞)
9 9
二、多选题(本大题共4小题,共20分。每小题有多项符合题目要求)
9.若{a }是公比为q的等比数列,记S 为{a }的前n项和,则下列说法正确的是( )
n n n
A. 若{a }是递增数列,则q>1
n
B. 若a >0,00,则S +S >2S
4 6 5
1
D. 若b = ,则{b }是等比数列
n a n
n
10.已知 ,若 ,且 ,则( )
A. B. 在 上的投影向量的坐标为
C. D.
11.定义 为a,b中较大的数,已知函数 ,给出下列结论,
其中正确的是( )
A. 的值域为
B. 是周期函数
C. 图象既有对称轴又有对称中心
D. 不等式 的解集为{x| }
2024届高三级11月四校联考数学试题
第 页,共 页
2 1(90分)
第二部分非选择题
三、填空题(本大题共4小题,共20分)
13.已知y=f(x)−x2为奇函数,且f(1)=3,则f(−1)= .
n
14.设S 是数列{a }的前n项和,且S =n2−cos π,则a = .
n n n 3 6
15.在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线
交AC于点D,且BD=1,则4a+3c的最小值为 .
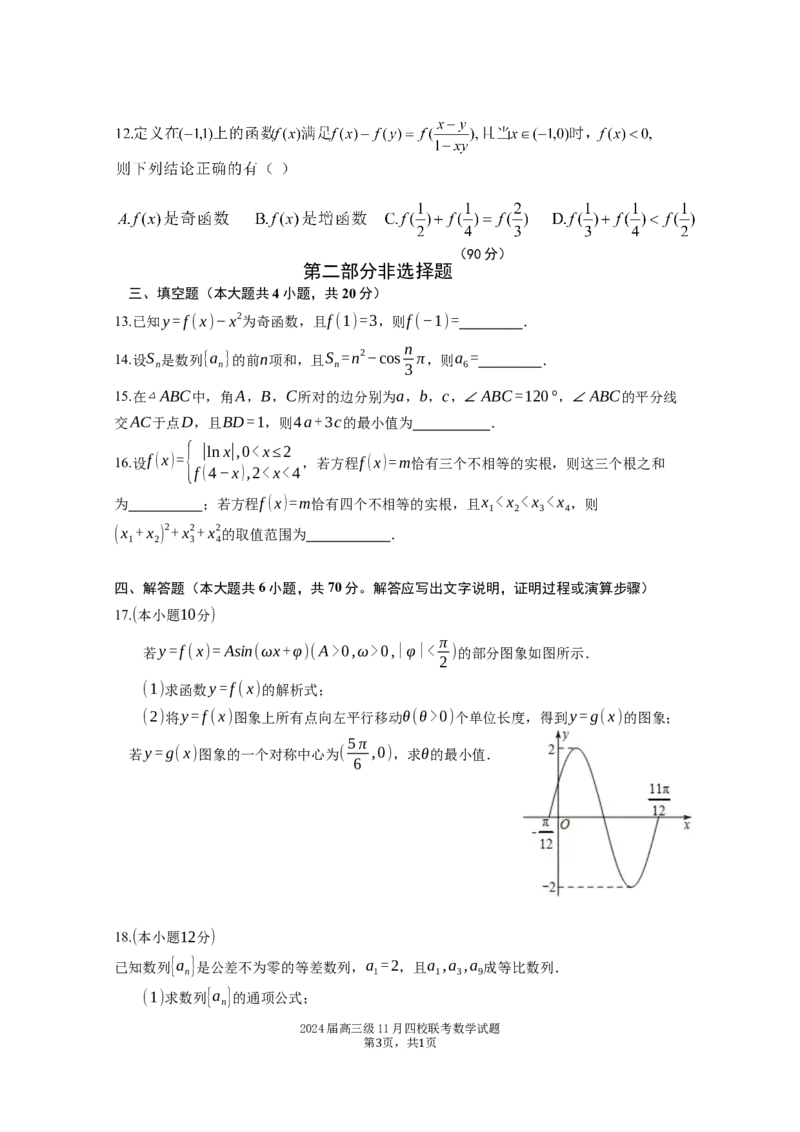
{ |lnx|,00,ω>0,|φ|< )的部分图象如图所示.
2
(1)求函数y=f(x)的解析式;
(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象;
5π
若y=g(x)图象的一个对称中心为( ,0),求θ的最小值.
6
18.(本小题12分)
已知数列{a }是公差不为零的等差数列,a =2,且a ,a ,a 成等比数列.
n 1 1 3 9
(1)求数列{a }的通项公式;
n
2024届高三级11月四校联考数学试题
第 页,共 页
3 11 1 1
(2)数列{b }满足b = , − =a ,求数列{b }的前n项和S .
n 1 2 b b n n n
n n−1
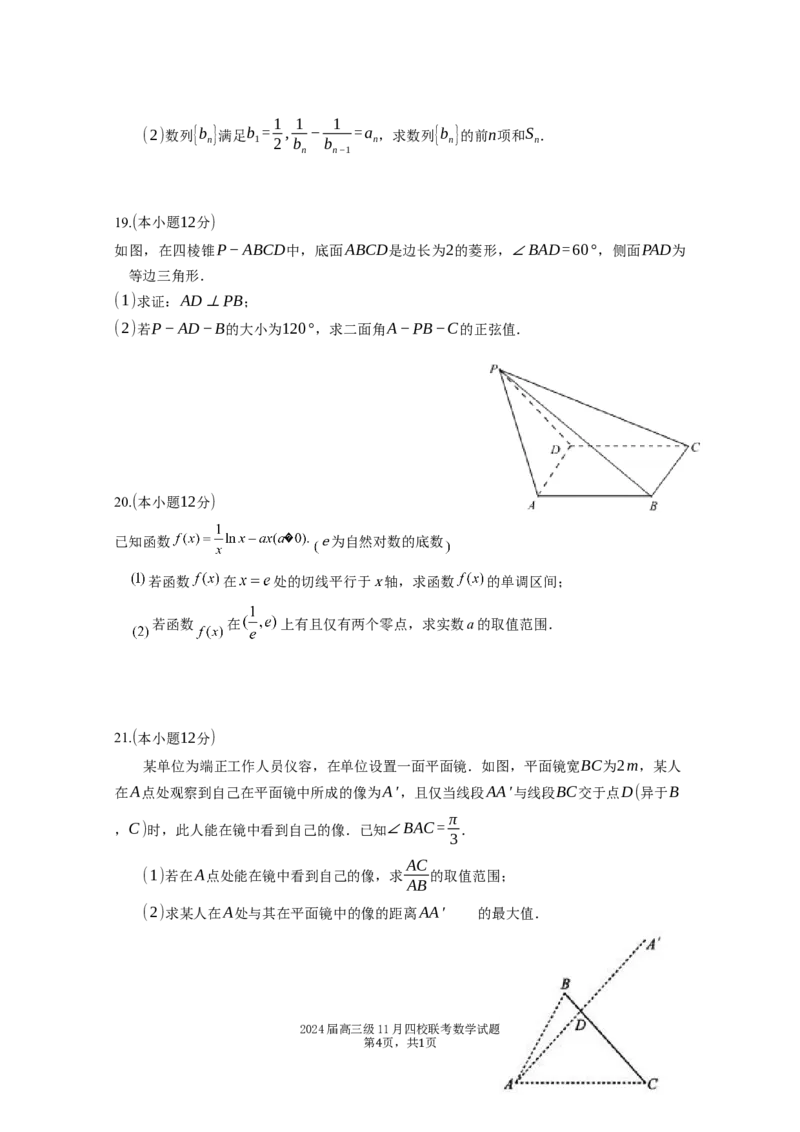
19.(本小题12分)
如图,在四棱锥P−ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,侧面PAD为
等边三角形.
(1)求证:AD⊥PB;
(2)若P−AD−B的大小为120°,求二面角A−PB−C的正弦值.
20.(本小题12分)
已知函数 为自然对数的底数
e
若函数 在 处的切线平行于 轴,求函数 的单调区间;
x
若函数 在 上有且仅有两个零点,求实数a的取值范围.
21.(本小题12分)
某单位为端正工作人员仪容,在单位设置一面平面镜.如图,平面镜宽BC为2m,某人
在A点处观察到自己在平面镜中所成的像为A′,且仅当线段AA′与线段BC交于点D(异于B
π
,C)时,此人能在镜中看到自己的像.已知∠BAC= .
3
AC
(1)若在A点处能在镜中看到自己的像,求 的取值范围;
AB
(2)求某人在A处与其在平面镜中的像的距离AA′ 的最大值.
2024届高三级11月四校联考数学试题
第 页,共 页
4 122、(本小题12分)
设函数 , ,
(1)当 时,求函数 的最小值;
(2)当 时,证明: ;
(3)证明:
2024届高三级11月四校联考数学试题
第 页,共 页
5 1