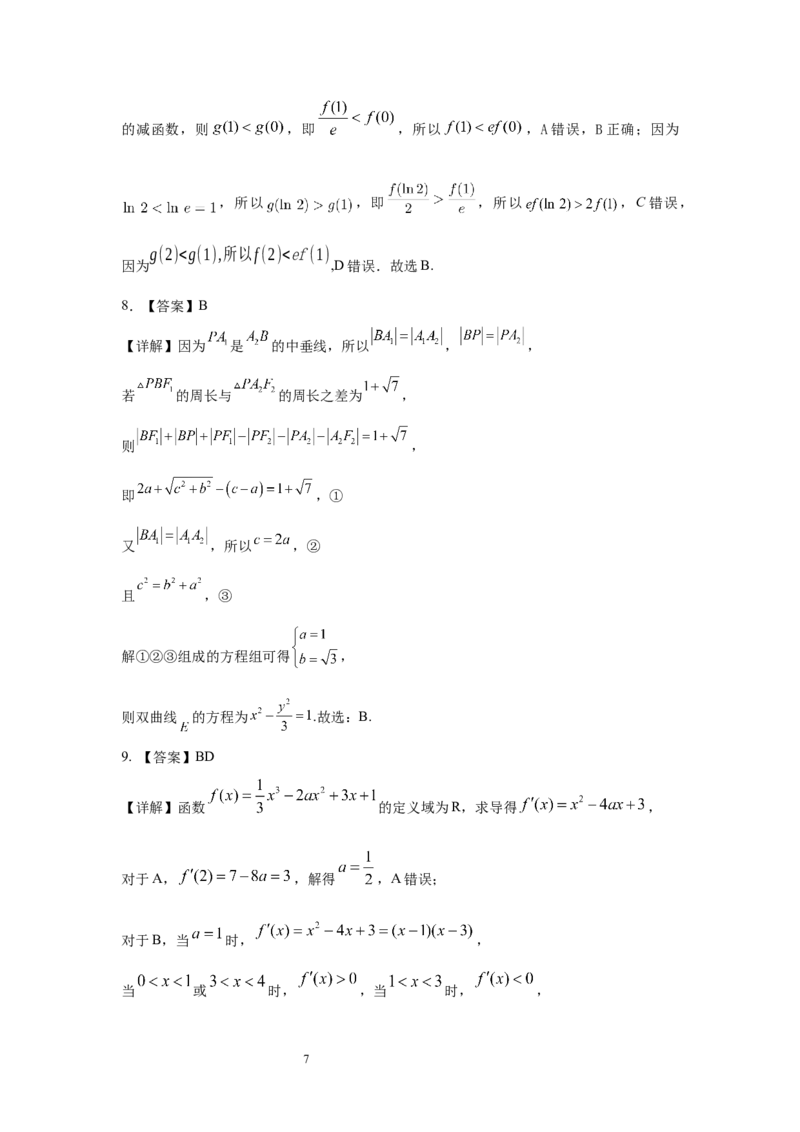文档内容
玉溪一中高 2026 届高二下学期月考试卷
数 学
考试时间:120分钟 满分:150分
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是
符合题目要求的.
1.已知 ,则 ( )
A. B. C. D.
2.已知等比数列 的前 项和为 ,若公比 , ,则 ( )
A.49 B.56 C.63 D.112
3.玉溪市正在创建全国文明城市,现有甲、乙、丙、丁 4人,平均分成两组,其中一组
指挥交通,一组打扫街道卫生,则甲、乙不在同一组的概率为( )
A. B. C. D.
4.设直线 的方向向量为 ,平面 的法向量为 ,则 是 的( )条件
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
5.已知点 是圆 上的动点,则点 到直线 距离的
最小值是( )
A.4 B.3 C.2 D.1
6.已知函数 ,若 恒成立,则实数a的取值范围是
A. B. C. D.
7.已知函数 的定义域为R,其导函数 满足 ,则
f(2)>ef(1)
A. B. C. D.
11
8.已知双曲线 的左,右焦点分别为 ,左,右顶点分别为
,点B的坐标为 在双曲线 上, 是 的中垂线,若 的周长与
的周长之差为 ,则双曲线 的方程为( )
A. B. C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.
9. 已知函数 ,则下列结论正确的是( )
A. 若 在 处的瞬时变化率为3,则
B. 当 时,函数 在区间 上的最小值为1
C. 若 在R上单调递增,则
5
D. 当 时,函数 图象的对称中心是(2, )
3
10.设等差数列 的前 项和为 , ,公差为 , , ,则下列结论正
确的是( )
A. B.当 时, 取得最大值
C. D.使得 成立的最大自然数 是17
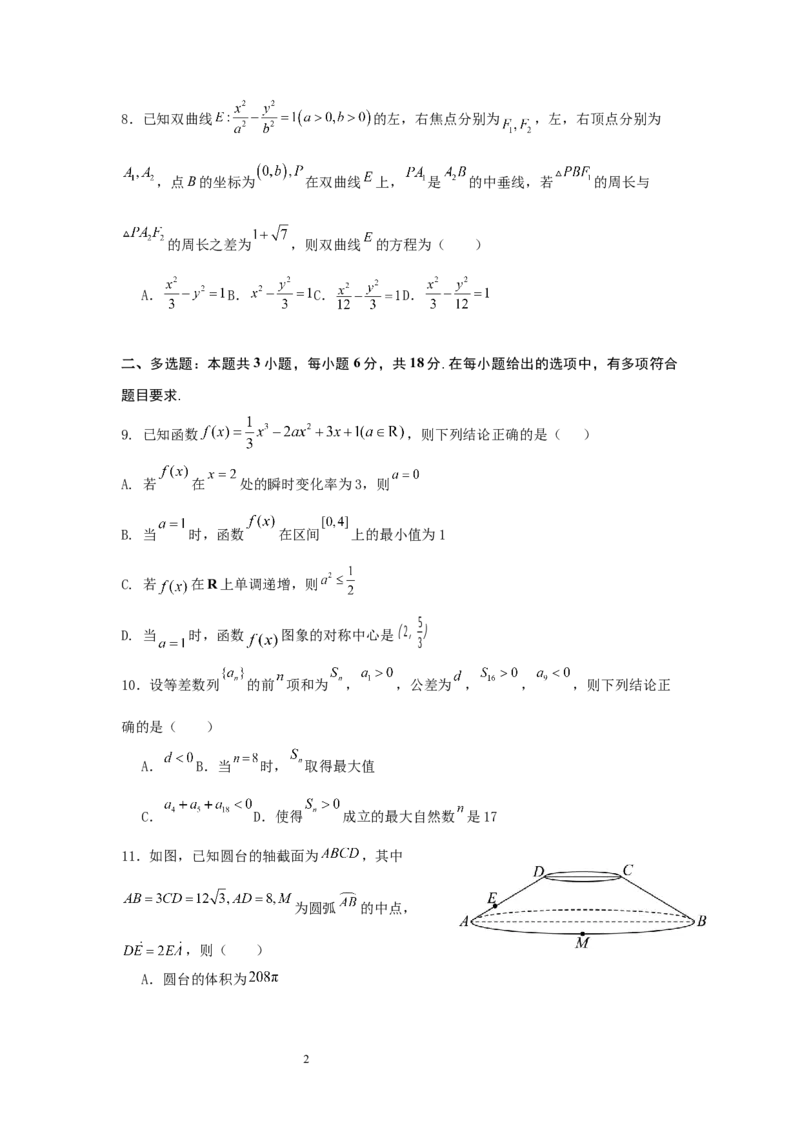
11.如图,已知圆台的轴截面为 ,其中
为圆弧 的中点,
,则( )
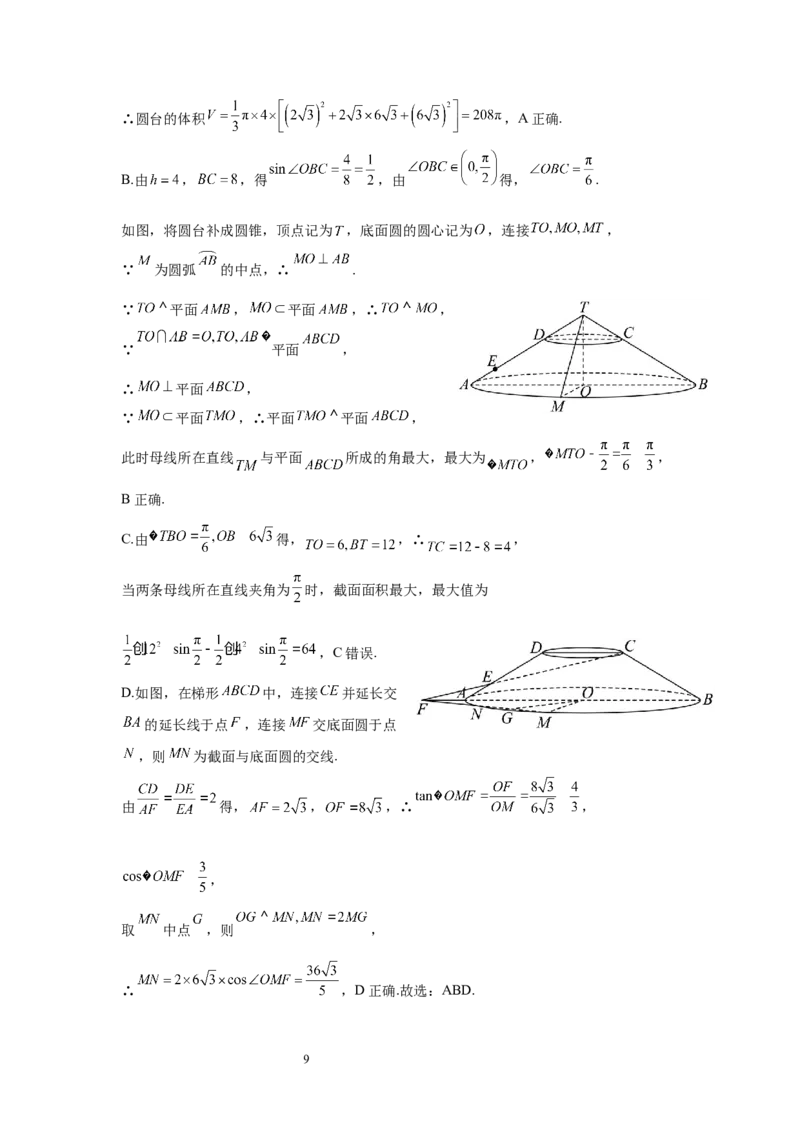
A.圆台的体积为
22
B.圆台母线所在直线与平面 所成角的最大值为
C.过任意两条母线作圆台的截面,截面面积的最大值为
D.过 三点的平面与圆台下底面的交线长为
三、填空题:本题共3小题,每小题5分,共15分.
12.抛物线 的焦点坐标是.
13.已知数列 满足 且 则 的通项公式 .
的
14. 若曲线 有两条过坐标原点 切线,则a的取值范围是________________.
四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(13分)在 中,角A,B,C的对边分别为a,b,c.已知 .
(1)求角A的大小;
(2)若 , ,求 的面积.
16.(15分)已知函数 .
(1)当 时,求函数 的极值;
(2)求 在 上的最大值 .
g(a)
33
17.(15分)已知椭圆 经过点
(1)求 的方程和离心率;
(2)若过点A且斜率为1的直线 与 的另一个交点为 ,求 的面积.
18.(17分)已知等差数列 满足 , 是关于 的方程 的两个根.
(1)求 和 ;
(2)求 和 ;
(3)设 ,求数列 的前 项和 .
19.(17分) 对于函数 的导函数 ,若在其定义域内存在实数 和 ,
使得 成立,则称 是“跃点”函数,并称 是函数
44
的“ 跃点”.
(1)若函数 是“ 跃点”函数,求实数 的取值范围;
(2)若函数 是定义在 上的“1跃点”函数,且在定义域内存在两个
不同的“1跃点”,求实数 的取值范围;
(3)若函数 是“1跃点”函数,且在定义域内恰存在一个“1跃点”,
求实数 的取值范围.
玉溪一中高 2026 届高二下学期月考试卷
数 学
参考答案
1.【答案】B
【详解】因为 ,所以 .故选:B
2.【答案】B
【详解】∵ ,∴ .故选:B.
3.【答案】C
【详解】根据指挥交通组选人打扫街道组选人,基本事件总数为6,
55
甲乙在同一组包含基本事件总数为2,其概率为 ,
其对立事件:“甲、乙不在同一组”
所以甲、乙不在同一组概率为 .故答案为:C
4.【答案】B
【详解】已知直线 的方向向量为 ,平面 的法向量为 ,则由 得到 或 ,
故 是 的非充分条件;
由 可得 ,故 是 的必要条件.故选:B
5.【答案】C
【详解】因为圆 可化为 ,
所以圆心坐标为 ,半径 ,
因为圆心 到直线 的距离 ,
所以直线 与圆 相离,
所以点 到直线 距离的最小值是 .故选:C.
6.【答案】A
【详解】若 恒成立,则 ,
, 由 ,得 ;由 ,得 ,
在 上单调递减,在 上单调递增, ,
由 ,得 ,故选:A
7.【答案】B
【详解】构造函数 , R,则 ,所以函数 为R上
66
的减函数,则 ,即 ,所以 ,A错误,B正确;因为
,所以 ,即 ,所以 ,C错误,
g(2)0,f(x)单调递增,当x∈(1,+∞)时, {f¿ ' (x)<0,f(x)单调递减¿
当
∴f(x)的极大值为f(1)=0,无极小值;
(2)由(1)知,当 时,函数 在 上单调递减,
此时, ;
当 时,函数 在 上单调递增,在 上单调递减,
此时, ;
当 时,函数 在 上单调递增,此时, .
1111
综上所述, .
17.【答案】(1) , ; (2)
【详解】(1)由题意得 解得
所以 的方程为 .
的离心率为 .
(2)由题意知直线 的方程为 ,
联立得 得 或 所以
观察可知 是等腰三角形,且 与 轴平行,所以
.
18.【答案】(1) , ; (2) , ;(2)
【详解】(1)设等差数列 的公差为 .
当 时, 是方程 的两根,
由韦达定理得 ,①
当 时, 是方程 的两根,
由韦达定理得 ,②
1212
由①②,解得 ;
(2)由(1)知 ,所以 ,
则 ,对于方程 ,
由韦达定理得 ,即 ,
(3) ,
所以
.
19.【答案】(1) ;(2) ; (3) .
【详解】(1)函数 的导函数为 ,
因为函数 , 是“ 跃点”函数,
则方程 有解,即 有解,
而 ,因此 ,解得 ,
所以实数 的取值范围是 .
(2)函数 的导函数为 ,
在
依题意,方程 ,即 上
有两个不等实根,
令 ,因此函数 在 上有两个不同零点,
则 ,解得 或 ,
1313
所以实数 的取值范围是 .
(3)函数 的导函数为 ,
因为函数 是“1跃点”函数,且在定义域内恰存在一个 “1跃点”,
则方程 ,显然 ,所以 在上恰有一个实根,
令 ,求导得 ,
由 ,得 ;由 ,得 且 , ,
于是函数 在 上单调递减, 恒成立,函数 的取值集合是
;函数 在 上单调递减,函数 的取值集合是 ;
函数 在 上单调递增,函数 的取值集合是 ,
函数 的图象,如图,
当 时,直线 与函数 的图象有唯一
公共点,即方程 恰有一个实数根,从而 ,
所以b的取值范围为 .
14