文档内容
保密★使用前
泉州市 2025 届高中毕业班质量监测(一)
2024.08
高 三 数 学
本试卷共 19 题,满分 150 分,共 8 页。考试用时 120 分钟。
注意事项:
1 .答题前,考生先将自己的姓名、准考证号填写在答题卡上。
2 .考生作答时,将答案答在答题卡上。请按照题号在各题的答题区域(黑色线框)
内 作答,超出答题区域书写的答案无效。在草稿纸、试题卷上答题无效。
3 .选择题答案使用 2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标
号; 非选择题答案使用 0.5 毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清
楚。
4.保持答题卡卡面清洁,不折叠、不破损。考试结束后,将本试卷和答题卡一并交回。
一、选择题: 本题共 8 小题,每小题 5 分,共 40 分。在每小题给出的四个选项中,只有一
项
是符合题目要求的。
1 .设集合
A . {0,1} B . {0,1, 4} C . {0,1, 4,9} D . {1, 4,9,16}
【命题意图】本小题主要考查集合的运算、不等式等知识;考查运算求解能力等;考查函数
与方程思想、化归与转化思想等;体现基础性,导向对发展数学运算等核心素
养的关注.
【试题解析】解法一:(排除法)因x = 0 符合题意,排除 D;因为x = 9 符合题意,排除
A,B; 故选 C .
解法二:因为A = = {x ∈ R ,所以A
, 故选 C .
2 .若复数z 满足z(1一 i) = 1+ i ,则 z4 =
A .1 B .一1 C .i D .16
【命题意图】本小题主要考查复数的概念、四则运算等基础知识;考查运算求解能力、推理
论证能力;考查化归与转化思想、函数与方程思想;体现基础性,导向对数学
运算等核心素养的关注.
高三数学试题 第 1 页(共 8 页)【试题解析】解法一:设z = a + bi(a, b ∈ R ) ,则(a + bi)(1一 i) = a + b+ (b一 a)i =
1+ i , 解得a = 0 ,b = 1 ,所以z = i ,所以 z4 = 1,故选 A .
解法二:因为z = 1 + i ,所以z = = i ,z4 = 1,故选 A .
解法三:方程两边同时平方,有 z2 . (一2i) = 2i ,所以 z2 = 一1 , z4 = 1 ,故选 A .
3 .已知向量a, b, c 满足| a |=| b| , a 与b 的夹角为 ,a + b + c = 0 ,则a 与c 的夹角为
A . B . C . D .
【命题意图】本小题主要考查向量的数量积等基础知识,考查运算求解等能力,考查化归与
转化,数形结合等思想,体现基础性,导向对发展数学运算等核心素养的关注.
【试题解析】解法一:设| a |=| b|= 1 ,由题得c = 一a一 b ,所以
a . c = a . (一a 一 b) = 一a 一 a . b = 一 | a | 一 | a | . | b |τ c o s = 1一 1 一
2 2
= 一 , 3
2 2
c2 = (一a 一 b)2 = a2 + 2a . b + b2 = 3 ,所以| c |= 3 ,
所以cos < a, c >= = 一 ,又< a, c >∈ 所以< a, c >=
故选 D .
解法二:建立直角坐标系,设| a |=| b|= 1 ,则a = (1,0) ,b = ( 1 , ) ,
2 2
所以c = 一a 一 b = ,所以a . c = 一 ,| c |=
所以cos < a, c >= = 一 ,又< a, c >∈
所以< a, c >=
故选 D .
解法三:运用向量运算的几何表示,构造平面图形,观察图形可快速得解.
4 .若sinθ + cosθ = 2 ,则 tanθ =
A .一 B .一 C . D .
高三数学试题 第 2 页(共 8 页)【命题意图】本小题主要考查三角函数的定义、三角恒等变换等知识,考查运算求解能力
等, 考查函数与方程思想、特殊与一般思想等,体现基础性,导向对发展直观
想象、
高三数学试题 第 2 页(共 8 页)数学运算、逻辑推理等核心素养的关注.
【试题解析】解法一:(特殊法)由题知sinθ = , cosθ = 满足条件,所以tanθ =
.
故选 C .
解法二:由题得 sinθ + cosθ = 1 ,所以
所以 = 2kτ + k ∈ Z ,所以θ =
2kτ + k ∈ Z tanθ = tan = tan .故
选 C .
解法三:由题得sin2 θ + 2 sinθcosθ + 3cos2 θ = 4 ,
所以3sin2 θ — 2 sinθcosθ + cos2 θ = 0,即 2 =
0 , 所以 sinθ — cosθ = 0 ,即tanθ = .故选 C .
解法四:由题得sinθ = 2 — cosθ , 所以(2 — 3 cosθ)2 + cos2 θ =
1 , 所以4cos2 θ — 4 cosθ + 3 = 0,即 ,
所以cosθ = ,sinθ = 2 — cosθ = 所以tanθ = .故选 C .
解法五:观察sinθ + cosθ = 2 ,知sin cosθ 同正,θ 为第一象限角,其
正 切值为正,排除 A ,B . 若 tanθ = ,可取 则sinθ + cosθ
= ,
不符合已知条件,排除 D,故应选 C .
4,
5 .若函数 在R 上单调递增,则实数 a 的取值范围是
A. (0,1) B .(1, 4] C .(1,8] D .(1,16]
【命题意图】本小题主要考查分段函数、基本初等函数、函数的单调性等知识,考查运算求
解能力、抽象概括能力等,考查函数与方程思想、转化和化归的思想等,体现
基础性和综合性,导向对发展数学运算、逻辑推理、数学抽象等核心素养的关
注.
高三数学试题 第 3 页(共 8 页)【试题解析】由指数函数的底数要求只讨论a > 0 且a ≠ 1,
高三数学试题 第 3 页(共 8 页)由题意得 一 3 为单调递增,故0 < a≤16 ,
又x < 4 时,f (x) = ax一3 为单调递增,故a > 1 ,
再由a1 ≤4+ 一1 ,即得a≤4 ,综上,1 < a≤4 ,
故选 B .
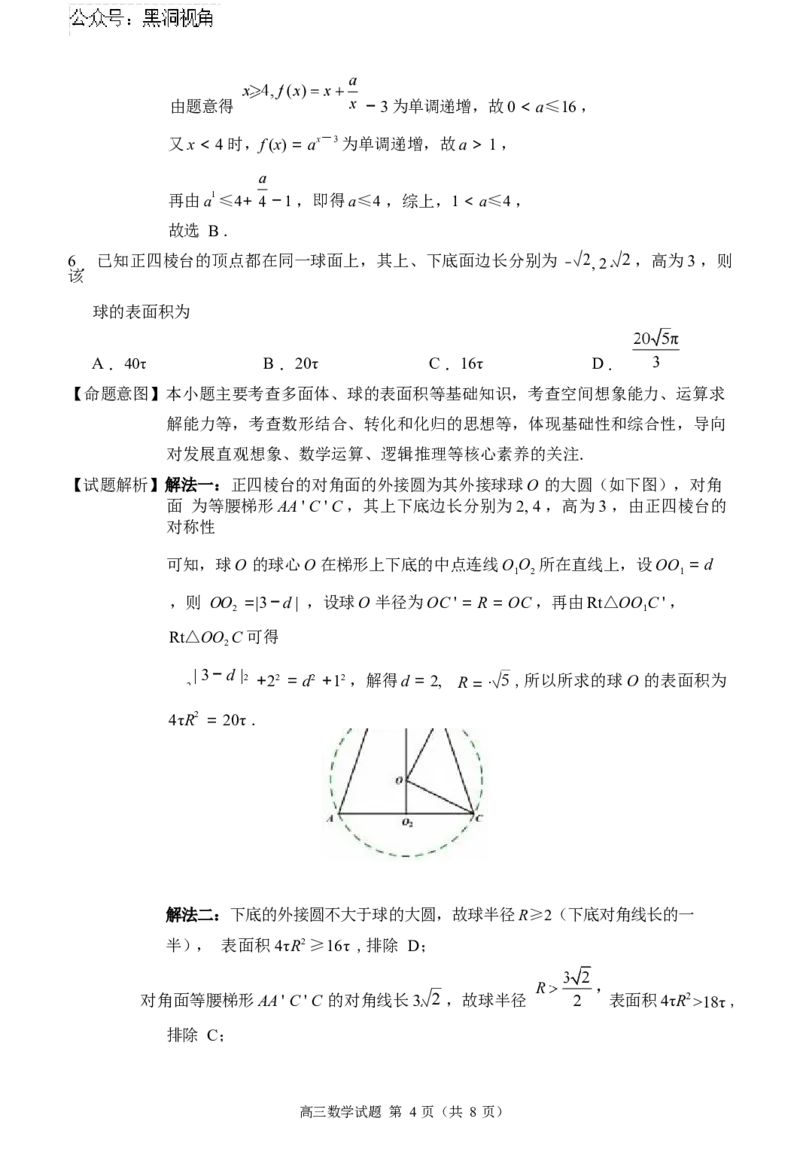
6 .已知正四棱台的顶点都在同一球面上,其上、下底面边长分别为 , 2 ,高为3 ,则
该
球的表面积为
A .40τ B .20τ C .16τ D .
【命题意图】本小题主要考查多面体、球的表面积等基础知识,考查空间想象能力、运算求
解能力等,考查数形结合、转化和化归的思想等,体现基础性和综合性,导向
对发展直观想象、数学运算、逻辑推理等核心素养的关注.
【试题解析】解法一:正四棱台的对角面的外接圆为其外接球球O 的大圆(如下图),对角
面 为等腰梯形AA ' C ' C ,其上下底边长分别为2, 4 ,高为3 ,由正四棱台的
对称性
可知,球O 的球心O 在梯形上下底的中点连线OO 所在直线上,设OO = d
1 2 1
,则 OO =|3 一d | ,设球O 半径为OC ' = R = OC ,再由Rt△OO C ' ,
2 1
Rt△OO C 可得
2
R2 | 3 一 d | 2 +22 = d2 +12 ,解得d = 2, R = · ,所以所求的球O 的表面积为
4τR2 = 20τ .
解法二:下底的外接圆不大于球的大圆,故球半径R≥2(下底对角线长的一
半), 表面积4τR2 ≥16τ ,排除 D;
对角面等腰梯形AA ' C ' C 的对角线长3 ,故球半径 表面积4τR2 >18τ ,
排除 C;
高三数学试题 第 4 页(共 8 页)若4τR2 =40τ , 则R = 易求球心到A ’ C ’的距离为d = 3 ,球心到AC 的
1
距
高三数学试题 第 4 页(共 8 页)离为d = · ,无法满足|d + d |= h = 3 ,或|d 一 d |= h = 3 ,故 A 不正
2 1 2 1 2
确. 故选 B .
7 .已知函数f (x) 满足f (x + y) = f (x) + f (y) + 2xy ,若f (1) = 1 ,则 f (25) =
A . 25 B .125 C .625 D .15625
【命题意图】本小题主要考查函数的基本性质、递推数列等基础知识;考查推理论证、运算
求解等能力;考查化归与转化、特殊与一般的函数思想;体现基础性,综合
性, 导向对逻辑推理、数学运算等核心素养的关注.
【试题解析】解法一:由题意取x = n(n∈ N), y = 1 ,可
得 f (n +1) = f (n) + f (1) + 2n
= f (n 一1) + 2f (1) + 2(n 一1) + 2n
= f (n 一 2) + 3f (1) + 2(n 一 2) + 2(n 一1) + 2n
= . . .
= (n +1)f (1) + 2(1 + 2 + . . .
+ n) = (n +1)f (1) + n(n + 1)
即知f (n) = nf (1) + n(n 一1) = n + n(n 一1) = n2 ,则f (25) =
625 . 故选 C .
解法二:令g(x)=f (x) 一 x2 , 则g(x + y) = f (x + y) 一 (x + y)2
= f (x) + f (y) + 2xy 一 (x + y)2 = f (x) + f (y) 一 x2 一 y2 = g(x) + g(y)
, 所以g(n) = g(n 一1) + g(1) = . . . = ng(1) = n(f (1) 一12 ) = 0 ,
即g(n) = f (n) 一 n2 = 0 ,所以f (n) = n2 ,则 f (25) = 625 .故选 C .
解法三:由f (x + y) = f (x) + f (y) + 2xy 可构造满足条件的函数f (x) = x2 ,
可以快速得到f (25) = 625
. 故选 C .
8 .已知函数 = cos x + cos 2x + cos 3x ,则
A . τ 是f(x) 的一个周期 B .x = τ 是f(x) 图象的一条对称轴
C . ( , 0) 是f (x) 图象的一个对称中心 D .f (x) 在区间(0, τ) 内单调递减
【命题意图】本小题主要考查三角函数的图象与性质、三角恒等变换等知识;考查推理论
高三数学试题 第 5 页(共 8 页)证能力、运算求解能力等,考查特殊与一般思想、函数与方程思想、化归与转化
思想等;体现基础性、综合性,导向对发展直观想象、逻辑推理、数学运算、数
学抽象等核心素养的关注.
【试题解析】解法一:(排除法)因为f = cos τ + cos 2τ + cos 3τ = 一1+ 一 = 一
= cos 0 + cos 0 + cos 0 = 1 + ,所以f ,故 A 错
误;
同理f (τ) ≠ 一f (0) ,故 C 错误;
因为 = cos cos τ + =
一
所以 ,故 D 错误.
故选 B .
解法二:因为f = cos cos 2 cos 3
所以f (x + τ) ≠ f (x) ,故 A 错误;
= 一 cos x + cos 2x 一 cos 3x ,所以f ,故 B 正确;
因为 = cos cos 2 cos 3 = cos x + cos 2x + cos 3x ,
所以一f (一x) ≠ f (x + τ) ,故 C 错误;
因为f ’(x) = 一sin x 一 sin 2x 一 sin 3x = 一[sin(2x 一 x) + sin(2x + x)] 一 sin 2x
= 一2sin 2x.cos x 一 sin 2x = 一sin 2x. (2cos x +1)
所以当 时,sin 2x > 0 ,2 cos x + 1 > 0 ,此时f ’
同理当 时,f ’ 当x∈ ( , τ)
时,f ’(x) < 0 ;
高三数学试题 第 6 页(共 8 页)τ τ 2τ
所以f (x) 在(0, ) 上单调递减,在( , ) 上单调递增,
2 2 3
高三数学试题 第 6 页(共 8 页)在 上单调递减,故 D 错误;
故选 B .
二、选择题:本题共 3 小题,每小题 6 分,共 18 分。在每小题给出的选项中,有多项符合
题
目要求。全部选对的得 6 分,部分选对的得部分分,有选错的得 0 分。
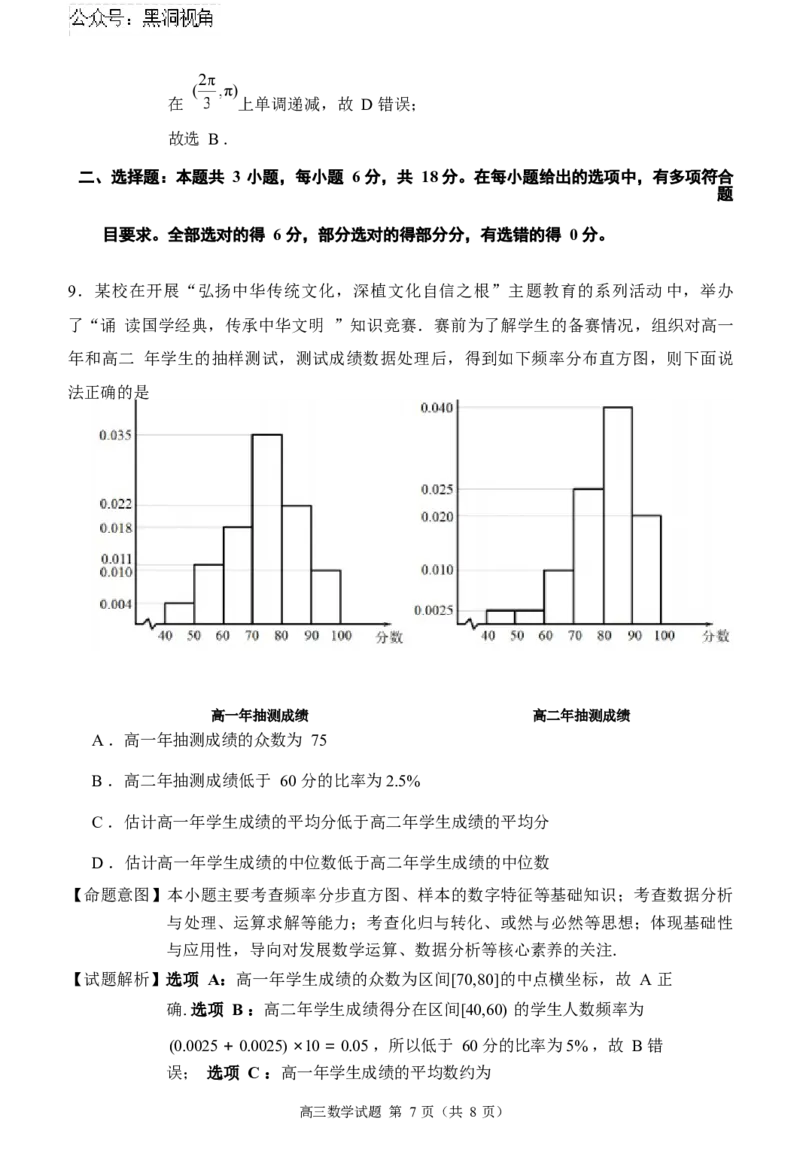
9.某校在开展“弘扬中华传统文化,深植文化自信之根”主题教育的系列活动中,举办
了“诵 读国学经典,传承中华文明 ”知识竞赛.赛前为了解学生的备赛情况,组织对高一
年和高二 年学生的抽样测试,测试成绩数据处理后,得到如下频率分布直方图,则下面说
法正确的是
高一年抽测成绩 高二年抽测成绩
A .高一年抽测成绩的众数为 75
B .高二年抽测成绩低于 60 分的比率为2.5%
C .估计高一年学生成绩的平均分低于高二年学生成绩的平均分
D .估计高一年学生成绩的中位数低于高二年学生成绩的中位数
【命题意图】本小题主要考查频率分步直方图、样本的数字特征等基础知识;考查数据分析
与处理、运算求解等能力;考查化归与转化、或然与必然等思想;体现基础性
与应用性,导向对发展数学运算、数据分析等核心素养的关注.
【试题解析】选项 A:高一年学生成绩的众数为区间[70,80]的中点横坐标,故 A 正
确. 选项 B :高二年学生成绩得分在区间[40,60) 的学生人数频率为
(0.0025 + 0.0025) ×10 = 0.05 ,所以低于 60 分的比率为5% ,故 B 错
误; 选项 C :高一年学生成绩的平均数约为
高三数学试题 第 7 页(共 8 页)45 × 0.04 + 55 × 0.11 + 65 × 0.18 + 75 × 0.35 + 85 × 0.22 + 95 × 0.1 =
74 分; 高二年学生成绩的平均数约为
45 × 0.025 + 55 × 0.025 + 65 × 0.1 + 75 × 0.25 + 85 × 0.4 + 95 × 0.2 =
80.75 分. 因为74< 80.75 ,故 C 正确.
选项 D :高一年学生成绩的中位数位于[70,80) ,高二年学生成绩的中位数位
于
[80,90) ,故 D 正
确. 故选 ACD .
10 .已知函数f (x) = ax3 - bx + 1 ,则
A .f (x) 的值域为R
B .f (x) 图象的对称中心为(0,1)
C .当ab < 0 时,f (x) 无极值
D .当b - 3a > 0 时,f (x) 在区间(-1,1) 内单调递减
【命题意图】本小题主要考查导数的应用、函数的基本性质等基础知识;考查推理论证、运
算求解等能力;考查数形结合、化归与转化等思想;体现基础性与综合性,导
向对发展直观想象、逻辑推理、数学运算等核心素养的关注.
【试题解析】A 选项:当a, b至少一个不为 0 ,则函数f (x) 为三次函数或者一次函
数, 值域均为R ;当a, b 均为 0 时,值域为{1} ,故 A 错误.
B 选项:函数g(x) = f (x) -1 = ax3 - bx 满足g(-x) = -ax3 + bx = -g(x)
, 可知g(x) 为奇函数,其图象关于 (0, 0) 中心对称,
所以f (x) 的图象为g(x) 的图象向上移动一个单位后得到的,
即关于(0,1) 中心对称,【或者用f (x) = 2 - f (-x)验证】,故 B 正确.
C 选项:f ’(x) = 3ax2 - b ,当 ab < 0 时,3ax2 - b恒大于0 或者恒小于0 ,
所以 函数f (x) 在R 上单调,无极值.故 C 正确.
D 选项:f ’(x) = 3ax2 - b ,当b - 3a > 0 时,取a = -1, b = -1 ,当x∈(-1,1)
时, f ’(x) = -3x2 + 1 ,f (x) 在区间(-1,1) 上不单调.D 选项错误;
另一方面,当b < 0 时,f ' = 3ax2 - b≥0 -1< - < 1 ,f 在
高三数学试题 第 8 页(共 8 页)[
b ]( (—1,1)) 单调递增. 故 D 错误.
3a 3a
故选 BC .
11 .在平面直角坐标系xOy 中,已知 F (—1,0), F (1,0) ,M(x, y) 是动点.下列命题正确的是
1 2
A .若| MF | + | MF |= 2 ,则 M 的轨迹的长度等于 2
1 2
B .若 MF — MF = 1 ,则 M 的轨迹方程为4x2 —
1 2
C .若| MF | . | MF |= 4 ,则 M 的轨迹与圆x2 + y2 = 6 没有交点
1 2
= 2 ,则 的最大值为 3
【命题意图】本小题主要考查曲线与方程、向量数量积等基础知识;考查运算求解、推理论
证等能力;考查化归与转化、数形结合、函数与方程等思想;体现基础性、综
合性与创新性,导向对发展数学运算、直观想象、逻辑推理、数学抽象等核心
素养的关注.
【试题解析】选项 A:因为| MF | + | MF |= 2 =| FF | ,所以M 的轨迹为线段
1 2 1 2
FF , 从而M 的轨迹的长度等于 2,故 A 正确.
1 2
选项 B :因为 MF MF ,由双曲线的定义知,
1— 2
=
M 的轨迹是以F, F 为焦点的双曲线的右支,而结论的方程中未限制范围,故
1 2
B
错误.(由c = 1, 2a = 1 ,得M 的轨迹方程为
选项 C:解法一:由|MF | . | MF |= 4 ,得 · (x +1) 2 + y2 . (x—1) 2 + y2 = 4 ,
化简 1 2
2 — 4x2 = 16,
得 2 — 4x2 = 16 ,联立 得x2 =
这与x2 ≤6 矛盾,所以方程组无解,故M 的轨迹与圆x2 + y2 = 6 没有交
点, 故 C 正确.
解法二:若有交点M(x, y) ,则MF . MF = (—1 — x, — y) . (1 — x, — y) = x2 + y2 —1 = 5 ,
1 2
又MF . MF =| MF | . | MF | cos < MF , MF >= 4 | cos < MF , MF > ≤4 ,矛
1 2 1 2 1 2 1 2
盾,所 以M 的轨迹与圆x2 + y2 = 6 没有交点,故 C 正确.
选项 D:
解法一:由 = 2 得,
高三数学试题 第 9 页(共 8 页)化简得 2 十 y2 =
所以M 的轨迹是以( , 0) 为圆心,半径为 的圆.
OM . OF 等于OM 在x 轴上的投影的长
2
度, 由图知其最大值为 3 ,故 D 正确.
解法二:同法一得M 的轨迹是以( , 0) 为圆心,半径为 的圆.
OM . OF = (x ,y) . (1,0) = x ,由圆的方程知x 可取到最大值
2
3, 故 D 正确.
解法三:由 = 2 得,
| MF | 一 | MF |=| MF | ≤| FF |= 2,| MO| ≤| OF | 十 | MF | ≤3 ,当M 在FF
1 2 2 1 2 2 2 2 1
的反向 延长线上时取等号.
① OM . OF =| MO | cos 7MOF ≤| MO |≤3 ;
2 2
②当M 在FF 的反向延长线上,且| MF |= 2 时,
2 1 2
满足条件 = 2 ,此时 .
所以OM . OF 的最大值为 3,故 D 正
2
确. 故选 ACD .
三、填空题:本题共 3 小题,每小题 5 分,共 15 分。
12 .若曲线y = ln x 在x = 2 处的切线与直线ax 一 y 十1 = 0 垂直,则a = .
【命题意图】本小题主要考查导数的几何意义、直线的位置关系等基础知识;考查运算求解、
推理论证等能力;考查化归与转化、数形结合、函数与方程等思想;体现基础
性与应用性,导向对数学运算、逻辑推理等核心素养的关注.
【试题解析】由题意得函数y = ln x 的导函数为 ,故在x = 2 处切线的斜率为
, 直线ax 一 y 十1 = 0 的斜率存在为a ,根据题意得 . a = 一1 ,解
得a = 一2 .
故答案为一2 .
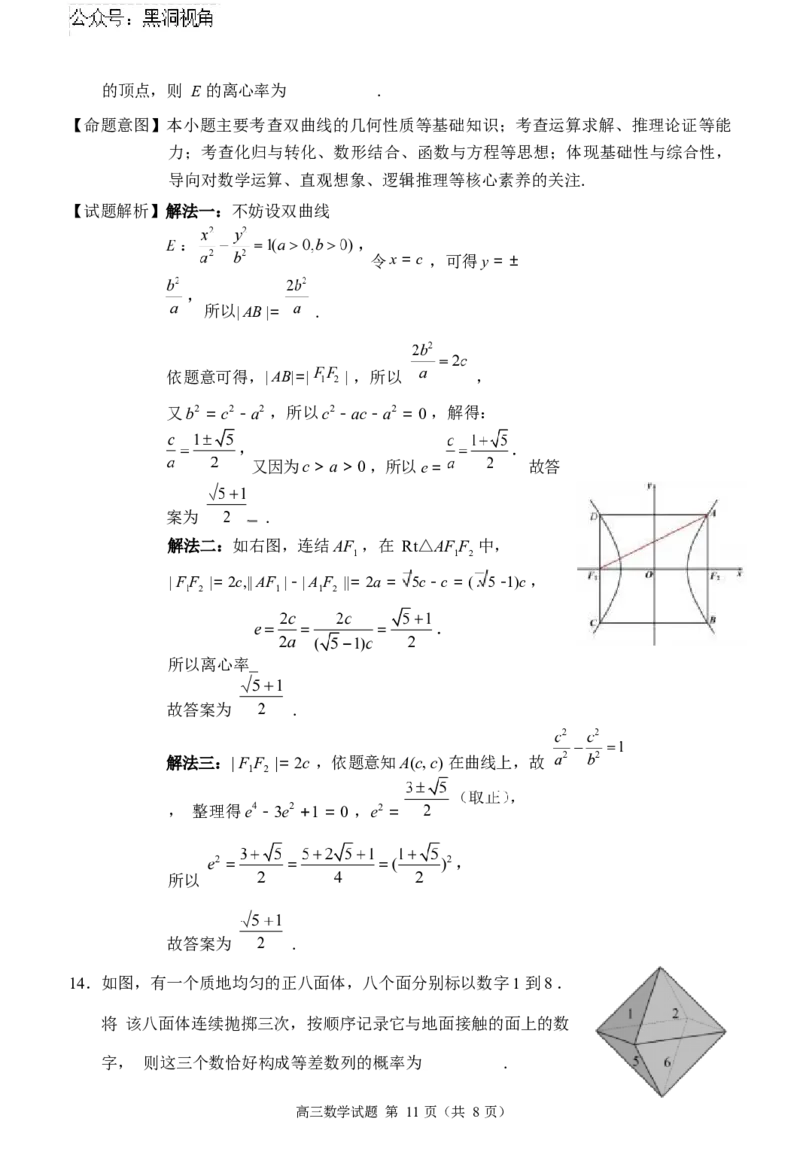
13 .过双曲线E 的两个焦点分别作实轴的垂线,交 E 于四个点,若这四个点恰为一个正方
形
高三数学试题 第 10 页(共 8 页)的顶点,则 E 的离心率为 .
【命题意图】本小题主要考查双曲线的几何性质等基础知识;考查运算求解、推理论证等能
力;考查化归与转化、数形结合、函数与方程等思想;体现基础性与综合性,
导向对数学运算、直观想象、逻辑推理等核心素养的关注.
【试题解析】解法一:不妨设双曲线
令x = c ,可得y = ±
所以| AB |= .
依题意可得,| AB|=| | ,所以 ,
又b2 = c2 - a2 ,所以c2 - ac - a2 = 0 ,解得:
又因为c > a > 0 ,所以e = 故答
案为 .
解法二:如右图,连结AF ,在 Rt△AFF 中,
1 1 2
| FF |= 2c,|| AF | - | A F ||= 2a = 5c - c = ( 5 -1)c ,
1 2 1 1 2
所以离心率
故答案为 .
解法三:| F F |= 2c ,依题意知A(c, c) 在曲线上,故
1 2
, 整理得e4 - 3e2 +1 = 0 ,e2 =
所以
故答案为 .
14.如图,有一个质地均匀的正八面体,八个面分别标以数字1 到8 .
将 该八面体连续抛掷三次,按顺序记录它与地面接触的面上的数
字, 则这三个数恰好构成等差数列的概率为 .
高三数学试题 第 11 页(共 8 页)【命题意图】本小题主要考查古典概型、计数原理等基础知识;考查推
理论证、运算求解等能力;考查分类与整合、或然与必然等思想;体现基础性
高三数学试题 第 11 页(共 8 页)与应用性,导向对发展数据分析、逻辑推理、数学运算、数学建模等核心素养
的关注.
【试题解析】由题意可知所有可能情况共有83 种,按顺序记录的三个数恰好构成等差数列,
可以按照公差为—3, —2, —1,0,1, 2,3 分类,其中公差为—3, —2, —1 和3, 2,1 的做
法数对 应相等.
公差为 0 的有(1,1,1),(2, 2, 2),...,(8,8,8) 共8 种做法;
公差为1 的有(1, 2,3),(2,3, 4), (6,7,8) 共 6 种做法,同公差为 —1 的;
公差为 2 的有(1,3,5),(2, 4,6),(3,5,7),(4,6,8) 共 4 种做法,同公差为 —2
的; 公差为3 的有(1, 4,7),(2,5,8) 共 2 种做法,同公差为 —3 的;
所以三个数恰好构成等差数列的概率
故答案为 .
高三数学试题 第 12 页(共 8 页)四、解答题:本题共 5 小题,共 77 分。解答应写出文字说明,证明过程或演算步骤。
15 .(13 分)
△ABC 的内角 A, B, C 所对的边分别为a, b, c ,已知
(1)求 A ;
(2)若 7BAC 的角平分线与BC 交于点D ,AD = 2 , AC = 2 ,求a + c .
【命题意图】本小题主要考查正弦定理、余弦定理等基础知识,考查逻辑推理能力、运算求
解能力等,考查函数与方程思想、数形结合思想等,体现基础性和综合性,导
向对发展直观想象、逻辑推理、数学运算等核心素养的关注。
【试题解析】(1)依题意,由正弦定理可得 ····1 分
所以sin C sinB sin( A B) , ·······················································2 分
又sin C sin[τ (A B)] sin(A B) , ···············································3 分
所以sin B sin(A B) sin(A B) 2cosAsin B , ································4 分
因为B e (0, τ) ,所以 sin B 0 ,所以cosA , ······························· 5 分
又A e (0, τ) ,所以 A . ·····························································6 分
(2)解法一:如图,由题意得,S S S , ·····················8 分
△ABD △ACD △ABC
1 τ 1 τ 1 τ
所以 c ADsin b ADsin b csin , ··································10 分
2 6 2 6 2 3
又 所以 , ·····················································11 分
所以a2 b2 c2 2bccos 9 ,即 a - 3 , ········································12 分
高三数学试题 第 13 页(共 8 页)所以 a c 3 . ·····································································13 分
解法二:如图, △ACD 中,因为AD 2 , AC 2 , ,
由余弦定理得, CD2 4 , ·····················8
分
所以 CD AD 2 , ······································································9
分
所以 , ···································································10
分
所以 , ·······························································11
分
所以 , ··············································12
分
所以 a c 3 . ·····································································13 分
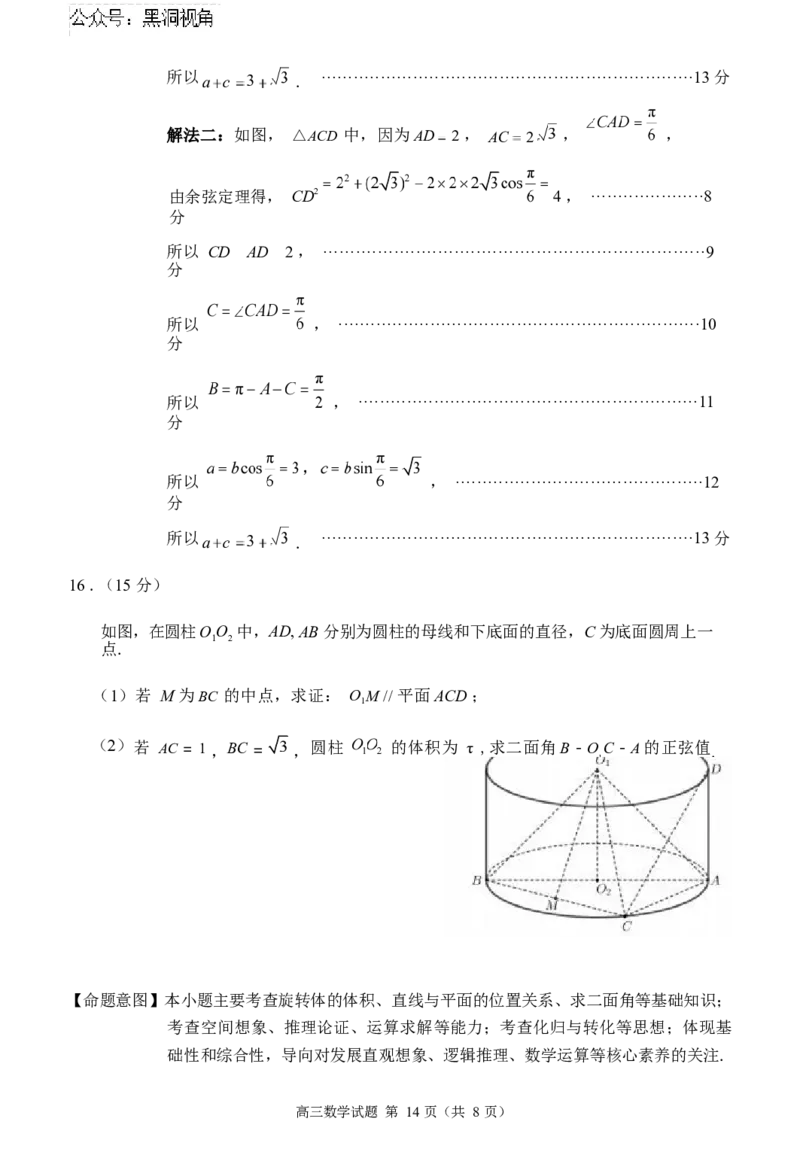
16 .(15 分)
如图,在圆柱OO 中,AD, AB 分别为圆柱的母线和下底面的直径,C 为底面圆周上一
1 2
点.
(1)若 M 为BC 的中点,求证: O M // 平面ACD ;
1
若 AC = 1 ,BC = ,圆柱 的体积为 τ ,求二面角B - O C - A的正弦值.
1
【命题意图】本小题主要考查旋转体的体积、直线与平面的位置关系、求二面角等基础知识;
考查空间想象、推理论证、运算求解等能力;考查化归与转化等思想;体现基
础性和综合性,导向对发展直观想象、逻辑推理、数学运算等核心素养的关注.
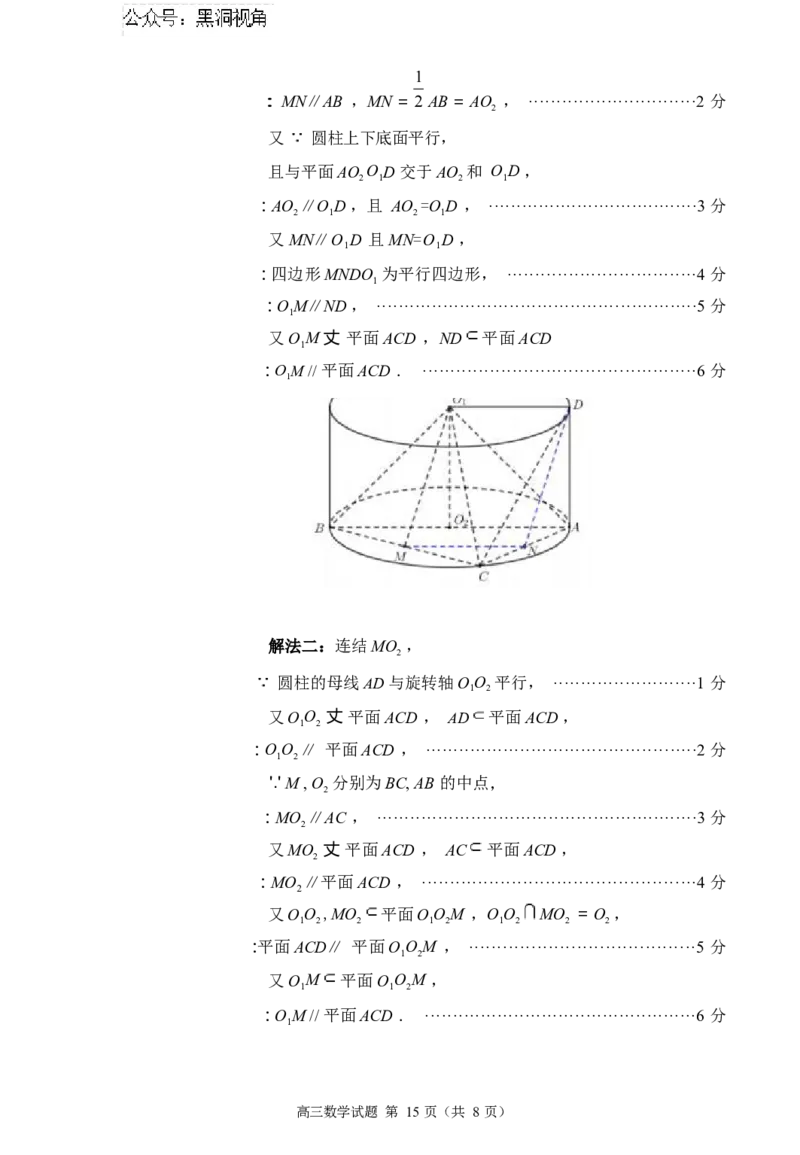
高三数学试题 第 14 页(共 8 页)【试题解析】(1)解法一:如下图,取AC 中点N ,连结MN, O D, DN ,
1
M, N 分别为BC, AC 的中点, ································1
分
高三数学试题 第 14 页(共 8 页): MN∥AB ,MN = AB = AO , ······························2 分
2
又 圆柱上下底面平行,
且与平面AO O D 交于AO 和 O D ,
2 1 2 1
: AO ∥O D ,且 AO =O D , ······································3 分
2 1 2 1
又MN∥O D 且MN=O D ,
1 1
: 四边形MNDO 为平行四边形, ··································4 分
1
: O M∥ND , ··························································5 分
1
又O M 丈 平面ACD ,ND 平面ACD
1
: OM // 平面ACD . ·················································6 分
1
解法二:连结MO ,
2
圆柱的母线AD 与旋转轴O O 平行, ··························1 分
1 2
又OO 丈 平面ACD , AD 平面ACD ,
1 2
: O O ∥ 平面ACD , ·················································2 分
1 2
'.' M , O 分别为BC, AB 的中点,
2
: MO ∥AC , ··························································3 分
2
又MO 丈 平面ACD , AC 平面ACD ,
2
: MO ∥平面ACD , ·················································4 分
2
又OO ,MO 平面OOM ,OO MO = O ,
1 2 2 1 2 1 2 2 2
:平面ACD∥ 平面O O M , ········································5 分
1 2
又O M 平面O O M ,
1 1 2
: O M // 平面ACD . ·················································6 分
1
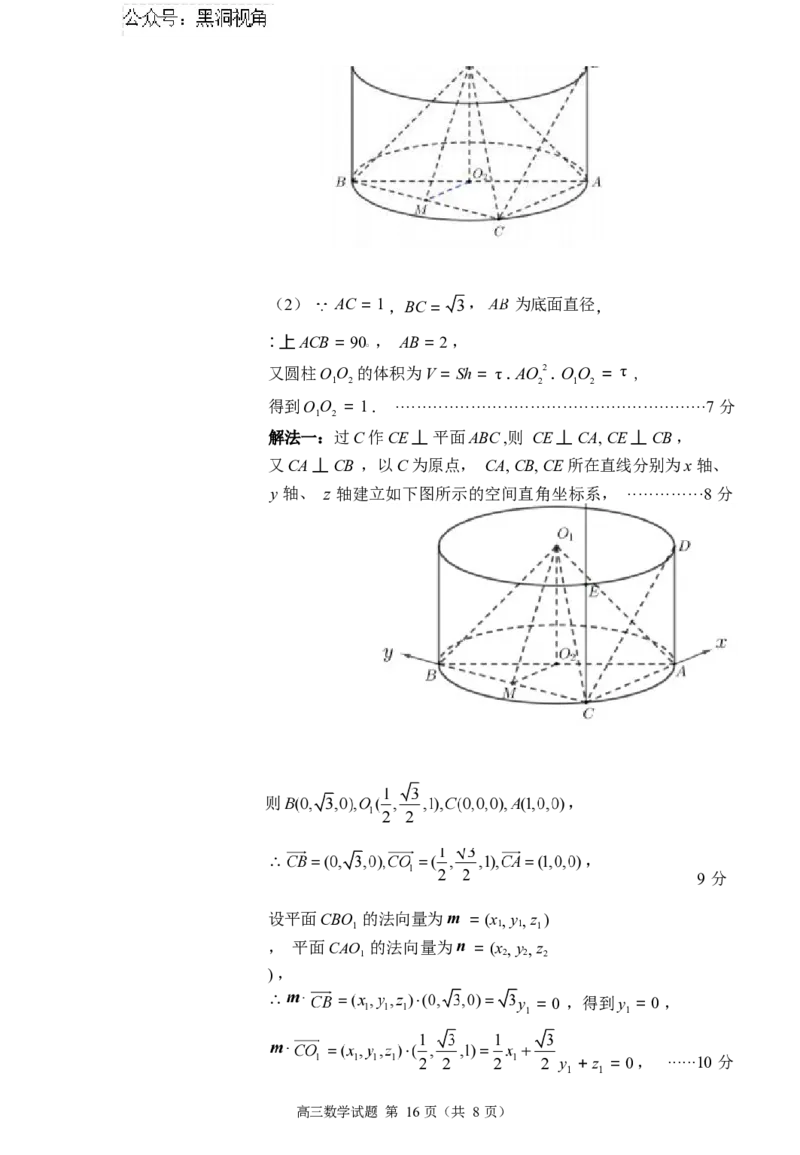
高三数学试题 第 15 页(共 8 页)(2) AC = 1 ,BC = 为底面直径,
: 上ACB = 90 , AB = 2 ,
又圆柱OO 的体积为V = Sh = τ . AO 2 . OO = τ ,
1 2 2 1 2
得到OO = 1 . ··························································7 分
1 2
解法一:过C 作CE 丄 平面ABC ,则 CE 丄 CA, CE 丄 CB ,
又CA 丄 CB ,以C 为原点, CA, CB, CE 所在直线分别为x 轴、
y 轴、 z 轴建立如下图所示的空间直角坐标系, ··············8 分
9 分
··············
设平面CBO 的法向量为m = (x, y, z )
1 1 1 1
, 平面CAO 的法向量为n = (x , y , z
1 2 2 2
) ,
y = 0 ,得到y = 0 ,
1 1
y + z = 0 , ······10 分
1 1
高三数学试题 第 16 页(共 8 页)取x = 2, z = -1 ,可得m =(2,0, -1) , ···························11 分
1 1
又n . CA = (x, y, z ) . (1,0,0) = 0 ,得到x = 0 ,
2 2 2 2
y + z = 0 , ···12 分
2 2
取y = 2 , z = - 可得 , ·······················13 分
2 2
设二面角B - O C - A 的大小为θ ,
1
则| cosθ |= , ······························14 分
即二面角B - O C - A 的正弦值为 . ·······················15 分
1
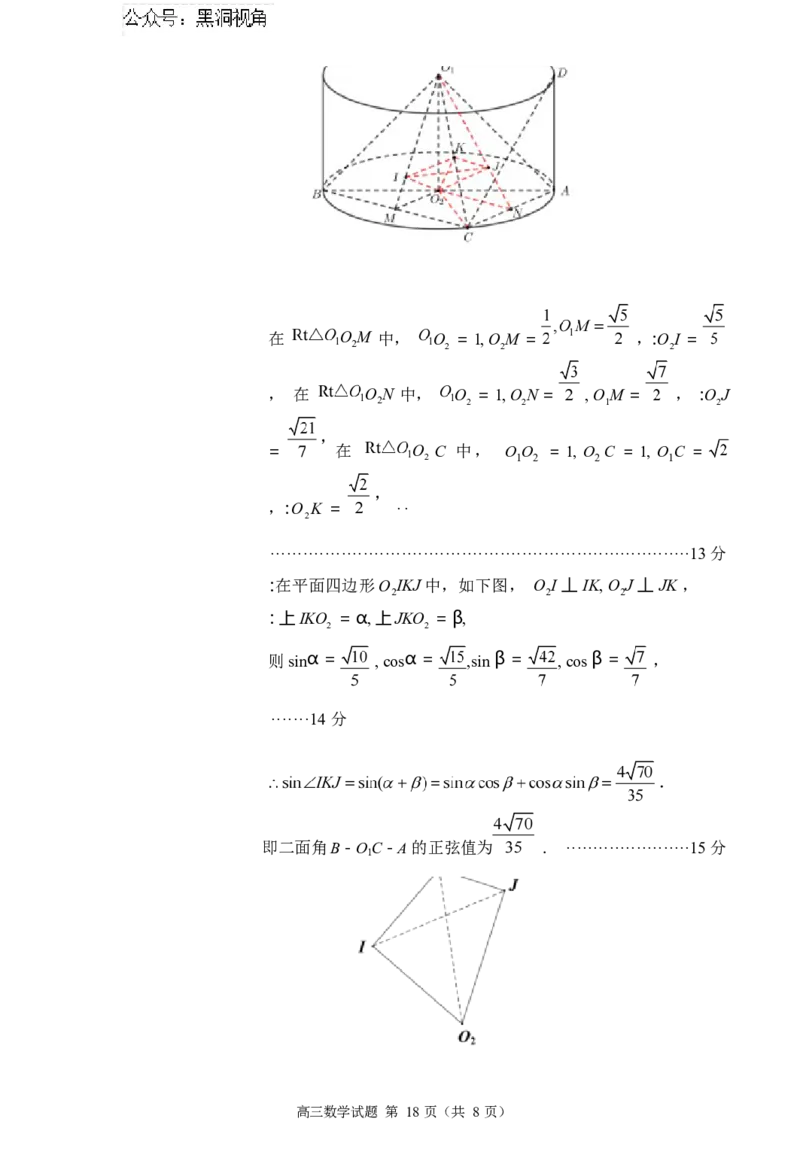
解法二:如下图,连结MO ,过O 作OI 丄 OM ,垂足 I
2 2 2 1
, 取 AC 中点N ,连结O N ,过O 作O J 丄 O N ,垂足
1 2 2 1
J ,
平面O IJ 交直线O C 于点K ,连结O K, IJ ,
2 1 2
M , O 分别为BC ,AB 的中点,
2
: MO ∥AC ,又 AC 丄 BC ,
2
: MO 丄 BC , ·························································8 分
2
OO 丄 平面ABC ,
1 2
: O O 丄 BC ,又MO O O = O ,
1 2 2 1 2 2
: BC 丄 平面O O M , ···············································9 分
1 2
O I 平面O O M , : BC 丄 O I
2 1 2 2
, 又OI 丄 OM ,BC OM = M ,
2 1 1
: O I 丄 平面BCO ,
2 1
同理可证O J 丄 平面ACO ,
2 1
: O I 丄 O C, O J 丄 O C, ,又O I O J = O ,
2 1 2 1 2 2 2
: O C 丄 平面O IJ ,即O C 丄 平面O IKJ , ···················10 分
1 2 1 2
: O C 丄 IK, O C 丄 JK , ·············································11 分
1 1
: 上IKJ 为二面角B - O C - A 的平面角, ·······················12 分
1
高三数学试题 第 17 页(共 8 页)在 O M 中, O = 1, O M = ,:O I =
2 2 2 2
, 在 O N 中, O = 1, ON = , OM = , :O J
2 2 2 1 2
= 在 O C 中, O O = 1, O C = 1, O C =
2 1 2 2 1
,:O K = ··
2
·············································································13 分
:在平面四边形O IKJ 中,如下图, O I 丄 IK, O J 丄 JK ,
2 2 2
: 上IKO = α, 上JKO = β,
2 2
则sinα = , cosα = ,sin β = , cos β = ,
·······14 分
即二面角B - O C - A 的正弦值为 . ·······················15 分
1
高三数学试题 第 18 页(共 8 页)17.(15 分)
已知椭圆 的左、右焦点分别为F , F ,离心率为 ,且经过点
1 2
(1)求 E 的方程;
(2)过F 且不垂直于坐标轴的直线l 交E 于 A, B 两点,点M为 AB 的中点,记△MF F
1 1 2
的
面积为S , △BFF 的面积为S ,求 的取值范围.
1 1 2 2
2
【命题意图】本题主要考查椭圆的标准方程、直线与椭圆的位置关系等基础知识;考查运算
求解、推理论证等能力;考查化归与转化、数形结合、函数与方程等思想;体
现基础性与综合性,导向对数学运算、直观想象、逻辑推理等核心素养的关注.
【试题解析 因为e2 = , ······················································1
分
所以5a2 = 9b2 , ···········································································2
分
因为点(2, ) 在椭圆上,所以 = 1 , ·······································3
分
即 = 1 ,解得a2 = 9 , ·························································4
分
所以b2 = 5 , ···············································································5
分
所以椭圆E 的方程为 . ·····················································6 分
【若方程求错,能体现 = 1, c2 = a2 - b2 各得 1 分】
(1)解法一:
由(1)得F (-2,0) ,依题意设l : x = my - 2(m≠0), ·····························7
1
分
1,
由 消去x ,得 y2 - 20my - 25 = 0 , ·························8 分
高三数学试题 第 19 页(共 8 页),
设 ,则 ······································9 分
设 ,则y =
o
高三数学试题 第 19 页(共 8 页), ·········································10 分
即 ································································11 分
因为m2 > 0,所以 0 < < ,所以- < < 0 ··················12 分
所以- 1 6< y 1 + + 2< 0 ,
5 y y
2 1
令 = t(t < 0且t ≠ -1) , ·······························································13 分
16 1 1
则- < t + + 2 < 0 ,解得-5 < t < - ,且t ≠ -1 , ................14 分
5 t 5
所以0 < t + 1 < 2 ,所以 的取值范围为(0, 2) . ·····························15 分
解法二:
由(1)得F (-2,0) ,依题意设l : y = k(x + 2)(k ≠ 0) , ····························7 分
1
由 消去y ,得 x2 + 36k2x + 36k2 - 45 = 0 , ················8 分
设 ,则 ,
,
所以 ·············································9 分
设M(x o, y
o
) ,则 y
o
= ,
高三数学试题 第 20 页(共 8 页), ····························10 分
令 , ·······························································11
分
,
则y = ty 代入 可得,
1 2
消去y 得: , ······················································12
2
分
因为k2 > 0 ,所以- < 0 , ··············································13
分
所以 解得-5< t < - ,且t ≠ -1 , ·························14
分
所以 所以 的取值范围为(0, 2) . ·····························15
分
18 .(17 分)
已知曲线 C : y = ln x , C : y = ex .
1 2
(1)证明:ex > ln x ;
(2)若曲线E 关于直线l 对称的曲线为E ,则称l 为E 与E 的一条对称轴.请写出C
1 2 1 2 1
与 C 的一条对称轴,并探究是否存在其它的对称轴;
2
(3)已知 A, B 是C 上的两点,A, B 是C 上的两点,若四边形ABB A 为正方形,其周
1 1 1 2 2 2 1 1 2 2
长为L ,证明:L > 4 - 2 .(参考数据:ln 2 ≈ 0.693, ≈ 1.649 )
【命题意图】本题主要考查基本初等函数、函数的单调性与对称性、导数的几何意义、导数
的应用等基础知识;考查运算求解、推理论证等能力;考查化归与转化、数形
高三数学试题 第 21 页(共 8 页)结合、函数与方程等思想;体现基础性、综合性与应用性,导向对数学运算、
直观想象、逻辑推理等核心素养的关注.
【试题解析】解法一:(1)要证原命题,只需证ex - ln x> 0 ,
设函数F(x) = ex - ln x ,其导函数为 = ex - , x > 0 , ···························1
分
高三数学试题 第 21 页(共 8 页)显然F’(x) 在(0, +∞) 单调递增,
且F’( ) = — 2 < 0 ,F’(1) = e —1 > 0 , ··············································2 分
1
x
故存在唯一的x ∈ ( ,1) 满足F (x ) =’ 0 , 即 e = 0 , ··························3 分
0 2 0 x
0
从而可得在(0, x ) F’(x) < 0 F(x) 单调递
0
减; 在(x , +∞) F’(x) > 0 F(x) 单调递
0
增;
所以F(x) 在x = x 处取到最小值F(x ) = ex0 — ln x , ·····························4 分
0 0 0
x
其中e0 = ,即x = — ln x ,
0 0
所以 + x ≥2> 0 . ·······························································5 分
0
故本题得证.
(2) C 与C 的一条对称轴为直线l : y = x , ·······································6 分
1 2
且l 是C 与C 的唯一对称轴, ··························································7 分
1 2
证明如下:由(1)分析得ex ≥1+ x ,当且仅当x = 0 时取等
号, 即曲线C 与直线l : y = x + 1相切于点Q(0,1) ,
2 2
且曲线C 在直线l 的上方(除点Q ); ···············································8 分
2 2
同理曲线C 与直线l : y = x —1 相切于点P(1,0)
1 1
, 且曲线C 在直线l 的下方(除点P );
1 1
而平行线l , l 的距离为 , ····························································9 分
1 2
故曲线C 上的任意点与C 上任意点的距离不小于
1 2
, 注意到P, Q 两点距离恰为 ,
故可得结论①:曲线C 上的任意点与C 上任意点的距离最小值为 ,
1 2
当且仅当这两点分别为P, Q 时取到. ·················································10 分
反证法:假设C 与C 存在除l 以外的其它对称轴
1 2
l’, 那么P 关于l’的对称点P’,
注意到P, Q 两点关于直线l : y = x 对称,故 P’在C 上且异于点Q ,
2
同理Q 关于l’的对称点Q’,其中Q’在C 上且异于点P ,
1
根据对称性可得 2 = |PQ| = |P’Q’| ,
高三数学试题 第 22 页(共 8 页)这与①矛盾,故假设不成立. 故l 是C 与C 的唯一对称轴. ···················11 分
1 2
(3)由题意,不妨设A (x ,ln x ) ,B (x , ln x ) ,B (x, ex3 ) , A (x, ex4 )
1 1 1 1 2 2 2 3 2 4
, 其中x < x < x , x < x < x ,
4 1 2 4 3 2
并由(2)分析得A , B 分别与A , B 关于直线y = x 对称,
1 1 2 2
可得A A 丄 l ,BB 丄 l ,且 x = ex3 , ln x = x , x = ex4 , ln x = x , ···········12
1 2 1 2 2 2 3 1 1 4 分
由正方形可得|BA | = |BB | ,即 2 (x — x ) = 2 (x
1 1 1 2 2 1 2
— x ) 所以x = x ,即正方形对角线AB 丄 x 轴,
3 1 3 1 2
因为|BB | = |AB | ,即 2 (ex 3 — ln x ) = 2 (ln x — ln x )
1 2 1 1 2 2 1
即
分
ex3 + ln x
1
= 2ln x
2 ...
② , ·······························································13
又因为x = x ,ln x = x ,所以②式可化为ex1 + ln x = 2x
1 3 2 3 1 1
故x 为方程ex + ln x — 2x = 0的根, ...............................14 分
1
即H(x) = ex + ln x — 2x(x > 0) 的零点为x ,
1
所以H(x) 在(0, +∞) 单调递增,
且H( ) = — ln 2 —1< 0 ,h(1) = e — 2 > 0 ,
所以 < x < 1 , ············································································15 分
1
所以正方形的边长|B B | = |ex3 — ln x | = ex1 — x , < x < 1 ,·················16 分
1 2 2 1 1
令φ(x) = ex — x(x > 0) ,且|BB | = φ(x ) ,
1 2 1
φ’(x) = ex —1 > 0 ,所以φ(x) 在(0, +∞) 单调递增,
则 即正方形的边长大于 — ,
所以正方形的周长L > 4 — 2 . ·························································17 分
解法二:(1)对任意x > 0,ln x < ex ,即证ex — ln x > 0 ,
先证明:ex —1≥x,即证 ex — x —1≥0 , ···············································1 分
设h(x) = ex — x —1,其导函数h'(x) = ex —1 , ·········································2 分
在区间(—∞,0), h'(x) < 0 ,h(x) 单调递减;
高三数学试题 第 23 页(共 8 页)在区间(0, +∞), h'(x) > 0 ,h(x) 单调递增;
故当且仅当x = 0 时 h(x) 取到最小值h(0) = 0 , ····································3
分
所以h(x)≥0 ,即 ex — 1≥x ;
同样也可得elnx —1 ≥ ln x,即 x —1 ≥ ln x ,即 x ≥ ln x + 1 ,
·························4 分
所以ex —1 ≥ ln x +1 ,即 ex — ln x≥2 > 0 ,
·············································5 分
本题得证.
(2)同解法一;
(3)同解法一.
19 .(17 分)
已知正整数p, q 满足p≤q ,正整数 满足a ≤p , = pq .对于确
i
定的 正整数 p, q ,记 的最小值为 f (p, q) .例如: 当 p = 2, q = 3 时, 2 × 3 = 22
+12 +12 或 2 × 3 = 12 +12 +12 +12 +12 +12 , a = 4 或6 ,f
i
当p = q = 3 时,写出 的所有值及f (3,3) 的值;
(2)探究f (3,3k + 1) (k ∈ N*) 的值;
证明: .
【命题意图】本题主要考查整数的离散性、数列的求和、不等式等知识,考查阅读理解能
力、 逻辑思维能力与创新能力等关键能力;考查数形结合思想、转化与化归
思想; 体现综合性、应用性与创新性,彰显高考的选拔特点,导向对发展数
学抽象、 逻辑推理、数学运算等核心素养的关注.
【试题解析】
(1) 的所有值为:3,5,7,9 , ···································4 分【写对 1 个得 1
分】
所以f (3,3) = 3 . ·············································································5 分
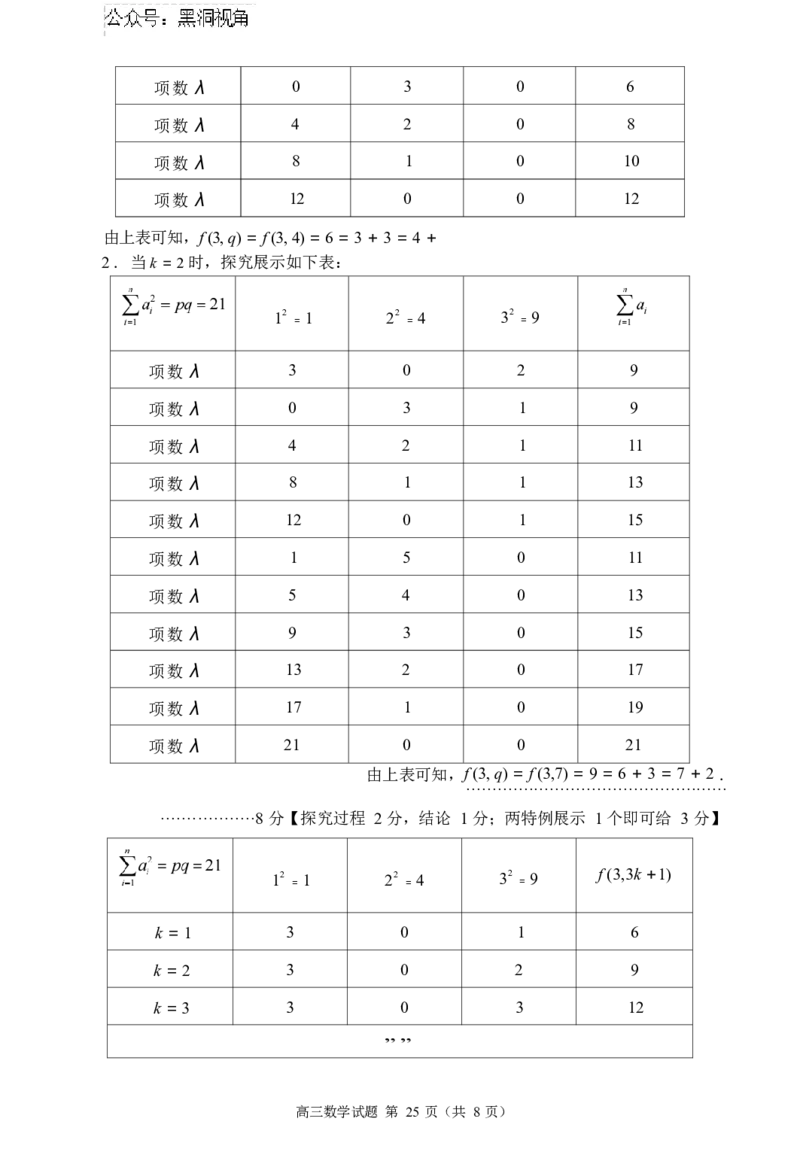
(2)当k = 1 时,探究展示如下表:
12 1 22 4 32 9
= = = Σ a
i
i1
项数 λ 3 0 1 6
高三数学试题 第 24 页(共 8 页)高三数学试题 第 24 页(共 8 页)项数 λ 0 3 0 6
项数 λ 4 2 0 8
项数 λ 8 1 0 10
项数 λ 12 0 0 12
由上表可知,f (3, q) = f (3, 4) = 6 = 3 + 3 = 4 +
2 . 当k = 2 时,探究展示如下表:
12 1 22 4 32 9
= = =
项数 λ 3 0 2 9
项数 λ 0 3 1 9
项数 λ 4 2 1 11
项数 λ 8 1 1 13
项数 λ 12 0 1 15
项数 λ 1 5 0 11
项数 λ 5 4 0 13
项数 λ 9 3 0 15
项数 λ 13 2 0 17
项数 λ 17 1 0 19
项数 λ 21 0 0 21
由上表可知,f (3, q) = f (3,7) = 9 = 6 + 3 = 7 + 2 .
··················································
··················8 分【探究过程 2 分,结论 1 分;两特例展示 1 个即可给 3 分】
12 1 22 4 32 9 f (3,3k +1)
= = =
k = 1 3 0 1 6
k = 2 3 0 2 9
k = 3 3 0 3 12
„„
高三数学试题 第 25 页(共 8 页)k = n 3 0 n 3n + 3
猜想q = 3k +1 (k ∈ N*) 时,f (3, q) = f (3,3k +1) = 3k + 3 = q + 2 .
······························
······································································· 9 分【结论正确 1 分】
证明如下:
a , a , , a 的各项的取值只有1, 2,3 三种可
1 2 n
能, 记其中取值为1, 2,3 的项数分别为λ ,λ
1 2
,λ .
3
取 = k ,有 = 3×12 + k × 32 = 9k
+ 3 , 此时 a = 3×1 + k × 3 = 3k + 3 .
i
假设3k + 3 不是 的最小值,则存在λ ' ,λ ' ,λ ' ∈ N ,
1 2 3
使得λ' + 4λ' + 9λ' = 9k + 3 ,且λ' + 2λ' + 3λ' ≤ 3k + 2 .
1 2 3 1 2 3
消去k ,得2 ,
因为 ∈ N ,所以 或 或
则若 则 N ;
若 则
N ; 若 则
N .
故矛盾.
所以,3k + 3 是 的最小值,f (3, q) = (3k +1) + 2 = q + 2 .
····························12 分【证明方法不唯一;能讲出一定的理由可给 1 分】
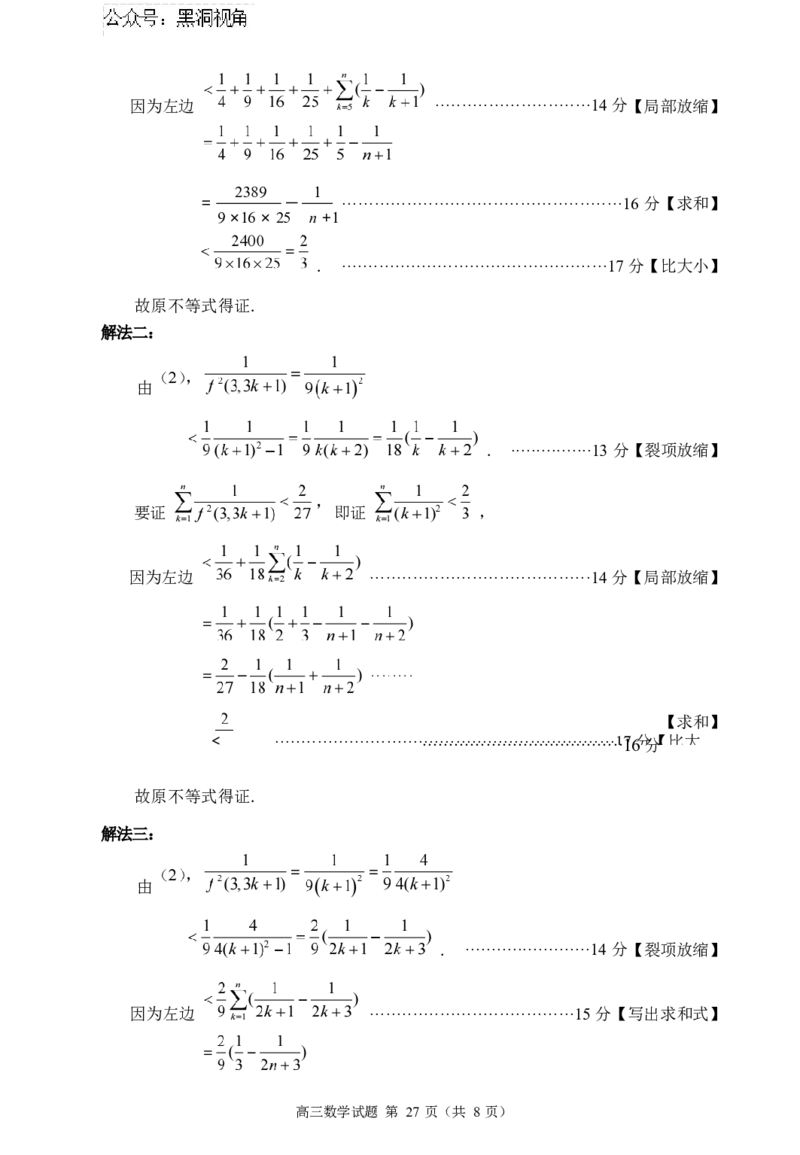
(3)解法一:
高三数学试题 第 26 页(共 8 页)由 ····13 分【裂项放
缩】 要证 即证 ,
高三数学试题 第 26 页(共 8 页)因为左边 ·····························14 分【局部放缩】
2389 1
= — ····················································16 分【求和】
9 ×16 × 25 n +1
. ··················································17 分【比大小】
故原不等式得证.
解法二:
由
. ················13 分【裂项放缩】
要证 即证 ,
因为左边 ·········································14 分【局部放缩】
< . ·····································································································1·17 6分 分【 比大
27
故原不等式得证.
解法三:
由
. ························14 分【裂项放缩】
因为左边 ······································15 分【写出求和式】
高三数学试题 第 27 页(共 8 页)·························································16 分
< . ································································17 分【比大小】
故原不等式得证.
高三数学试题 第 28 页(共 8 页)