兰州一中2023-2024-1学期期中考试高三数学试题(1)_2023年11月_0211月合集_2024届甘肃省兰州第一中学高三上学期11月期中_甘肃省兰州第一中学2024届高三上学期11月期中数学

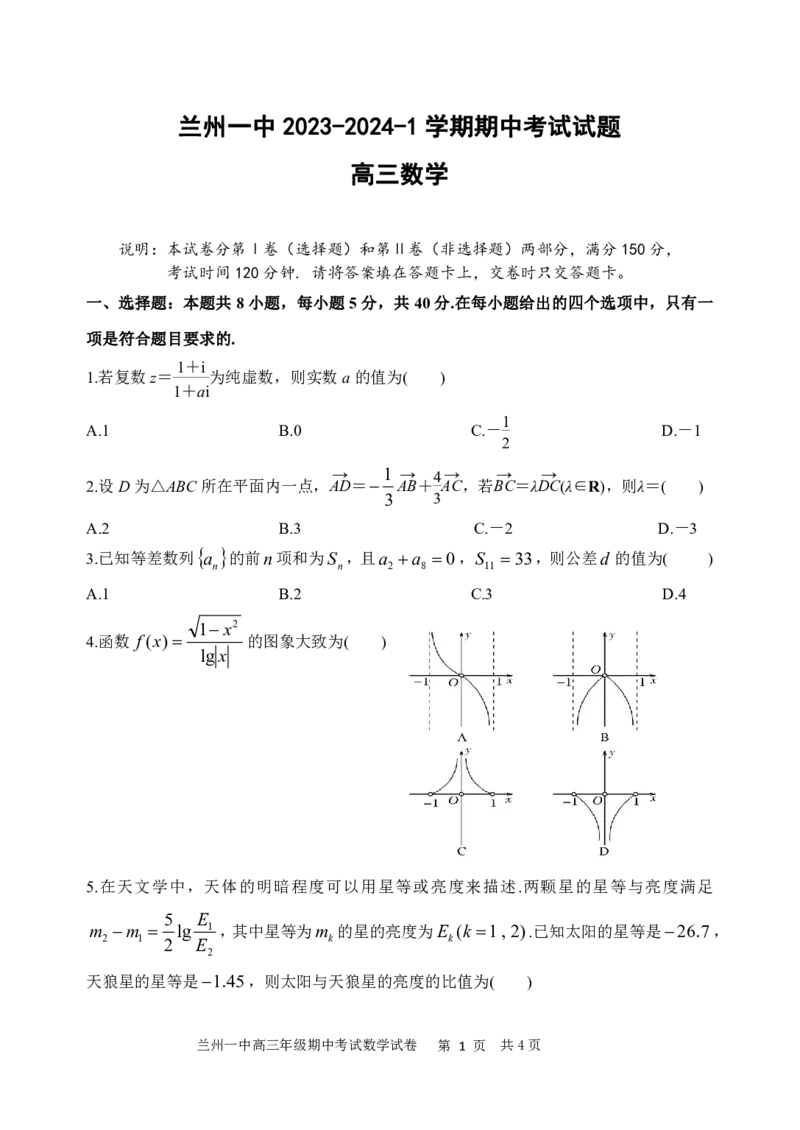
兰州一中 2023-2024-1 学期期中考试试题 高三数学 说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分， 考试时间120分钟. 请将答案填在答题卡上，交卷时只交答题卡。 一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一 项是符合题目要求的. 1＋i 1.若复数z＝ 为纯虚数，则实数a的值为( ) 1＋ai 1 A.1 B.0 C.－ D.－1 2 → 1 → 4→ → → 2.设D为△ABC所在平面内一点，AD＝ AB＋ AC，若BC＝λDC(λ∈R)，则λ＝( ) 3 3 A.2 B.3 C.－2 D.－3   3.已知等差数列 a 的前n项和为S ，且a a 0，S 33，则公差d 的值为( ) n n 2 8 11 A.1 B.2 C.3 D.4 1x2 4.函数 f(x) 的图象大致为( ) lgx 5.在天文学中，天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足 5 E m m  lg 1 ，其中星等为m 的星的亮度为E (k 1, 2).已知太阳的星等是26.7， 2 1 2 E k k 2 天狼星的星等是1.45，则太阳与天狼星的亮度的比值为( ) 兰州一中高三年级期中考试数学试卷 第 1 页 共4页 {#{QQABDYIUgggoAAAAAAgCEwEgCgIQkBECAIoOQBAIMAIBQRNABAA=}#}A.1010.1 B.10.1 C.lg10.1 D.1010.1 6.在ABC中，内角A,B,C的对边分别为a,b,c. 若向量m(a,cosA)， n(cosC, 2bc)，且mn0，则角A的大小为( ) π π π π A. B. C. D. 6 4 3 2 7.若log (2ab)1log ab ，则a2b的最小值为（ ） 3 3 8 16 A.6 B. C.3 D. 3 3 8.已知函数 f(x) ln( x2 1x) ，设a  f(log 4)，b f(30.2)，c f(31.1)， 3 则( ) A.a bc B.ba c C.ca b D.cba 二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符 合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分.  9.已知函数 f(x)sin(2x )，则下列结论正确的是( ) 6  A.x 是函数 f(x)图象的一条对称轴； 3 7 B.( ,0)是函数 f(x)图象的一个对称中心； 12  C.将函数 f(x)图象向右平移 个单位所得图象的解析式为 f(x)cos2x； 6   D.函数 f(x)在区间[ , ]内单调递增. 6 3 lnx 10.对于函数 f(x) ，下列说法正确的是( ) x 1 A.f(x)在x＝e处取得极大值 ； B.f(x)有两个不同的零点； e C.f(4)＜f(π)＜f(3)； D.4 4 . 兰州一中高三年级期中考试数学试卷 第 2 页 共4页 {#{QQABDYIUgggoAAAAAAgCEwEgCgIQkBECAIoOQBAIMAIBQRNABAA=}#}  11.已知等差数列 a 是递增数列，其公差为d ，前n 项和为S ，且满足a  3a ，则 n n 7 5 下列结论正确的是（ ） A.d  0 B.a  0 1 C.当n  5 时，S 最小 D.当S  0 时，n 的最小值为8 n n 12.已知函数 f  x  及其导函数g  x  的定义域均为R.且满足 f  2x  f  42x  ， f  x  f x 0，当x 2,4  时，g x 0，g  1 1，则（ ） A. f  x  的图象关于x1对称 B. g  x  为偶函数 C. g  x g  x4 0 D. 不等式g  x 1的解集为  x 18k  x18k,kZ  三、填空题：本题共4小题，每小题5分，共20分． 3 13.已知tanθ＝3，则cos( 2)＝________. 2 14.函数f(x)＝Asin(ωx＋φ)(A＞0，ω＞0，|φ|＜π)的部分图象如图所示，则函数f(x)的解析式 为________. 15.已知向量a (3,1)，b(t,1)，a,b45，则b 在a 方向上的投影向量的坐标为 _______. x  1 16.将函数 f(x)2cos2 cos(x )图象上所有点的横坐标变为原来的 ，再向左平 2 3 2  移(0)个单位长度，得到函数g(x)的图象，若对任意的xR，均有g(x) g( )成 12 立，则的最小值为__________. 兰州一中高三年级期中考试数学试卷 第 3 页 共4页 {#{QQABDYIUgggoAAAAAAgCEwEgCgIQkBECAIoOQBAIMAIBQRNABAA=}#}三、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． （17题10分；18-22题每题12分.) 17.已知数列  a  的前n项和S 2n12，数列  b  满足b  S (nN). n n n n n     (1)求数列 a 的通项公式； (2)求数列 b 的前n项和T . n n n 18.为了降低能源损耗，某体育馆的外墙需要建造隔热层，体育馆要建造可使用20年的隔 热层，每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位：万元) k 与隔热层厚度x(单位：cm)满足关系：C(x)＝ (0 x10，k为常数)，若不建隔热层， 3x＋5 每年能源消耗费用为8万元，设f(x)为隔热层建造费用与20年的能源消耗费用之和. (1)求k的值及f(x)的表达式； (2)隔热层修建多厚时，总费用f(x)达到最小？并求最小值. 19.已知ABC中内角A,B,C的对边分别为a,b,c，向量m(2sinB, 3)， B n(cos2B,2cos2 1)，B为锐角且m//n. 2 (1)求角B的大小； (2)如果b2，求S 的最大值. ABC 20.在锐角三角形ABC中，内角A,B,C所对的边分别为a,b,c，且 3cosCsinC  3b, 且a 1. (1)求ABC的外接圆的半径； (2)求2bc的取值范围. 21.设函数 f(x)＝2lnx－mx2＋1. (1)讨论函数 f(x)的单调性； (2)当 f(x)有极值时，若存在x ，使得 f(x ) m－1成立，求实数m的取值范围. 0 0 1 22．(本小题12分）已知函数 f(x)xeax的极值为 ． e (1)求a的值并求函数 f(x)在x1处的切线方程； 兰州一中高三年级期中考试数学试卷 第 4 页 共4页 {#{QQABDYIUgggoAAAAAAgCEwEgCgIQkBECAIoOQBAIMAIBQRNABAA=}#}lnx (2)已知函数g(x)emx  (m0)，存在x(0,)，使得g(x)„0成立，求m的最大值． m 兰州一中高三年级期中考试数学试卷 第 5 页 共4页 {#{QQABDYIUgggoAAAAAAgCEwEgCgIQkBECAIoOQBAIMAIBQRNABAA=}#}