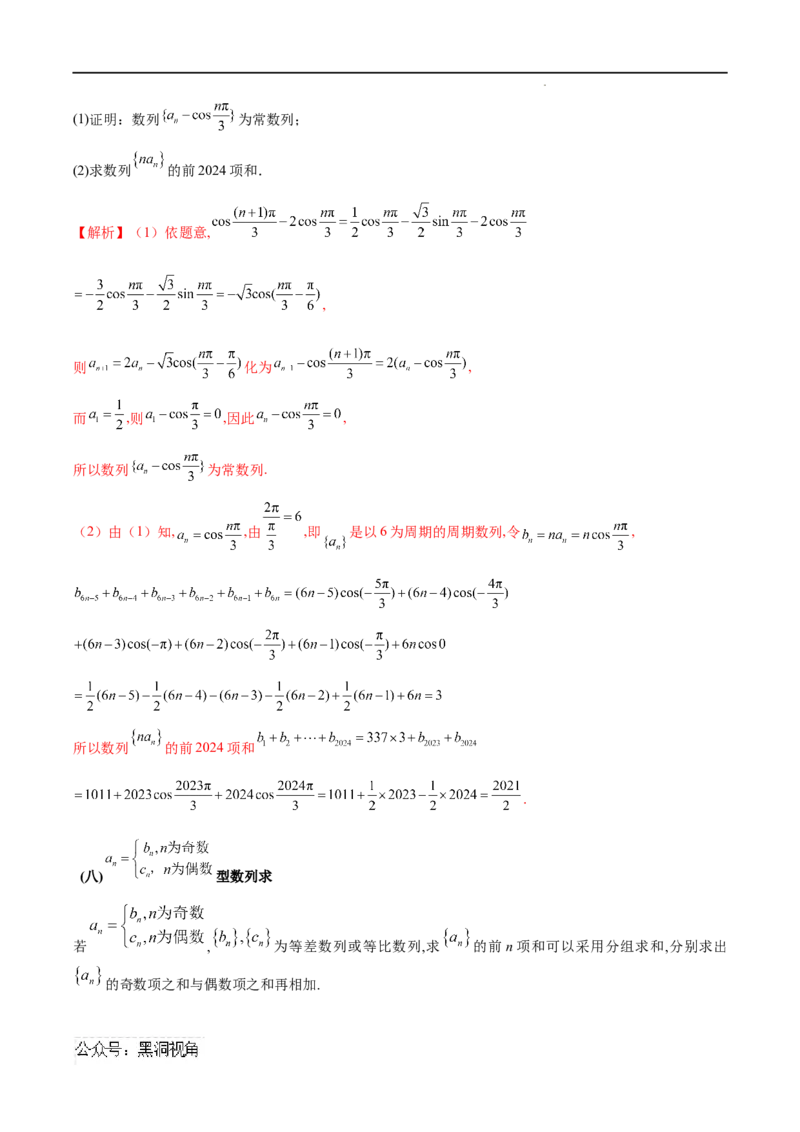文档内容
专题 3 数列求和
新高考在试题形式、试卷结构、难度调控等方面深化改革,数列解答题的难度增加,作为压轴题出现
的概率变大,数列求和是数列中的两大基本题型题型之一,也是高考中的热点,本专题总结数列求和的基本
方法,供大家参考.
(一)等差数列求和
若一个数列为等差数列或可以转化为等差数列,求和时可以利用等差数列前n项和公式.
【例1】(2024届河北省沧州市沧县中学高三下学期模拟)设正项数列 的前n项和为 ,已知
.
(1)求数列 的通项公式;
(2)设 ,求数列 的前n项和 .
【解析】(1)由 ,得 ①,
当 时, ,解得 (负值舍去).
当 时, ②,
① ②,得 ,
化为 ,
学科网(北京)股份有限公司因为 , ,解得 ,
所以数列 是首项为3、公差为2的等差数列,
所以 ,即 .
(2)由(1)知 ,所以 ,
从而 ,
则 , ,…, ,
以上n个式子相加,得 .
(二)等比数列求和
若一个数列为等比数列或可以转化为等比数列,求和时可以利用等比数列前n项和公式.
【例2】已知数列 的前n项和为 , ,数列 是公比为2的等比数列.
(1)求
(2)若 ,求 的前2n项的和.
【解析】(1) 数列 是公比为2的等比数列,且 ,
所以 ,
当 时 ,
所以 .
(2)因为 为奇数时 ,n为偶数时 ,
所以 的奇数项为0,偶数项构成公比为 的等比数列,
学科网(北京)股份有限公司所以 的前2n项的和为 .
(三)倒序相加求和
把数列分别正着写和倒着写再相加,即等差数列求和公式的推导过程的推广,一般来说,若数列 满足
,求数列 的前n项和,可用倒序相加法.
【例3】已知函数 ,数列 满足 ,则数列 的前2025项的和
【解析】因为 ,所以 ,
有 .
记数列 的前 项和 ,又 ,所以
.所以 .
(四)裂项求和
把数列的通项拆成两项之差求和,正负相消剩下首尾若干项.(1)用裂项相消法求和时,要对通项进行变换,如:
=(-), ,裂项后可以产生连续相互抵消的项.(2)抵消后并不一定只剩下第一项和最后一项,也有可能前面剩
两项,后面也剩两项.
【例4】(2024届天津市南开区高三下学期质量监测二)已知 是等差数列,公差 , ,且
是 与 的等比中项.
(1)求 的通项公式
(2)数列 满足 ,且 .
学科网(北京)股份有限公司(ⅰ)求 的前n项和 .
(ⅱ)是否存在正整数m,n( ),使得 , , 成等差数列,若存在,求出m,n的值;若不存在,请说明
理由.
【解析】(1)因为 为等差数列,且 ,所以 .
又 是 与 的等比中项,所以 ,即 .
化简得 ,解得 或 (舍),
所以 .
(2)(i)由 ,得 ,所以 ( ),又 ,
当 时,
,
又 也适合上式,所以 ,
则 ,
所以 .
(ⅱ)假设存在正整数m,n,使得 , , 成等差数列,
则 ,即 ,整理得 ,
显然 是25的正约数,又 ,则 或 ,
当 ,即 时, 与 矛盾;
学科网(北京)股份有限公司当 ,即 时, ,符合题意,
所以存在正整数使得 , , 成等差数列,此时 , .
拓展:裂项求和常见变形
1.
= .
2.
= .
3.
= .
4.
= .
5.
=
学科网(北京)股份有限公司=
= .
6.
=
7.
1 1 1 1 1 1
= 2−1 -22 −1+22 −1-23 −1+ +2n −1-2n+1 −1
1
=1-
2n+1 −1
.
8.
=
9.
=
10.
=
=
学科网(北京)股份有限公司a
n + 1
11.
=
=
12.
=
=
13.
=
=
3 4 5 n+2
14.
1×2×22 +2×3×23 +3×4×24
+ +
n(n+1)2n+1
1 1 1 1 1 1
− − −
=
2 2×22 +2×22 3×23
+ +
n.2n (n+1)2n+1
1 1
−
=
2 (n+1)2n+1
15.若 是各项均不为零,且公差 的等差数列,则
学科网(北京)股份有限公司= =
(五)错位相减法求和
主要用于一个等差数列与一个等比数列对应项相乘所得的数列的求和,即等比数列求和公式的推导过程的推
广.错位相减法求和时的注意点:
(1)要善于识别题目类型,特别是等比数列公比为负数的情形;
(2)在写出“S”与“qS”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“S -qS”的表达
n n n n
式;
(3)在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.
【例5】(2024届浙江省绍兴市柯桥区三模)已知数列 的前n项和为 ,且 , ,设
.
(1)求证:数列 为等比数列;
(2)求数列 的前 项和 .
【解析】(1) ,即 ,
即 ,则 ,即 ,
即 ,又 ,
故数列 是以 为首项、以 为公比的等比数列.
(2)由(1)易得 ,即 ,则 ,
则 ,
有 ,
则
学科网(北京)股份有限公司,
故 .
(六) 为等差(比)数列,可并项求 的前n项和
若 , 为等差数列或等比数列,求 的前n项和可以采用,即把相邻两项的和看作一项,构造
一个新数列求和
【例6】若数列 满足 .
(1)求数列 的前100项的和;
(2)若 ,求数列 的前31项的和.
【解析】(1)数列 的前100项的和为
= .
(2)若 ,数列 的前31项的和为
= .
(七)周期型数列求和
周期数列求和一般采用并项求和,即把一个周期内的所有项求和,构成一个新数列求和,求形如 数
列的和,一般根据正弦型函数的最小正周期,对n进行分类,然后再采用并项求和
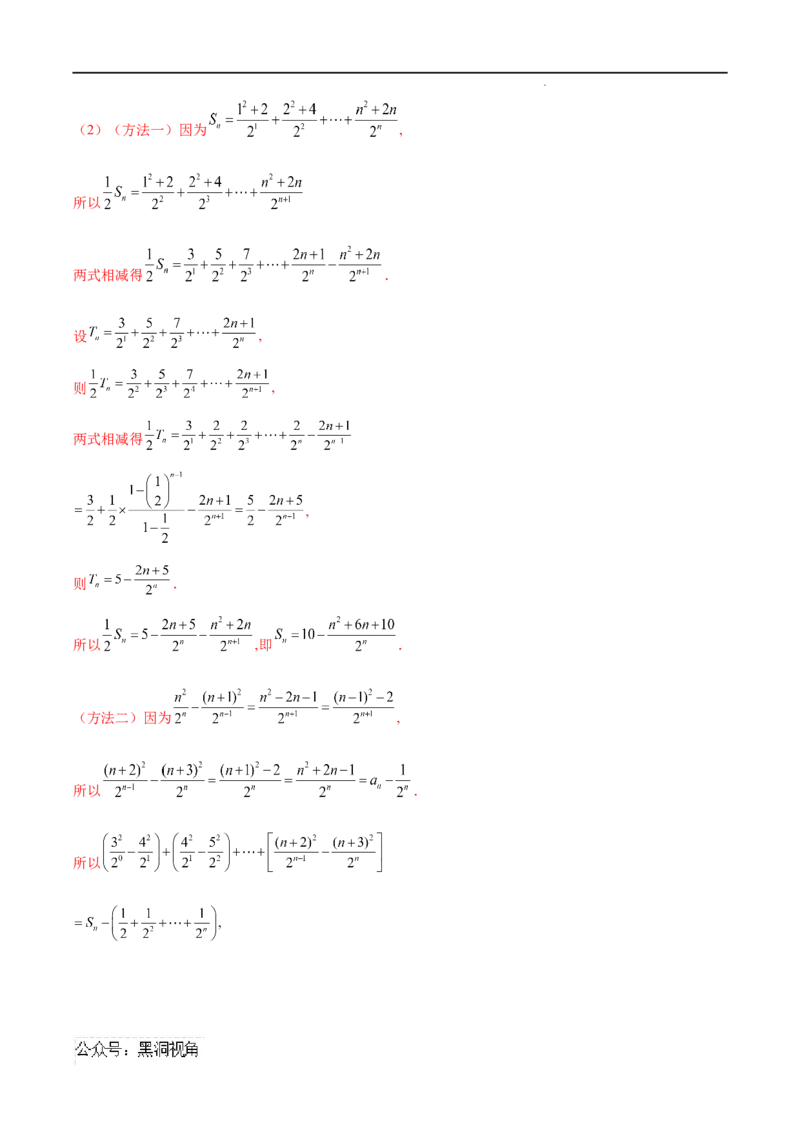
【例7】(2024届福建省福州第一中学高三下学期5月模拟)已知数列 中, ,
.
学科网(北京)股份有限公司(1)证明:数列 为常数列;
(2)求数列 的前2024项和.
【解析】(1)依题意,
,
则 化为 ,
而 ,则 ,因此 ,
所以数列 为常数列.
(2)由(1)知, ,由 ,即 是以6为周期的周期数列,令 ,
所以数列 的前2024项和
.
(八) 型数列求
若 , 为等差数列或等比数列,求 的前n项和可以采用分组求和,分别求出
的奇数项之和与偶数项之和再相加.
学科网(北京)股份有限公司【例8】(2024届广东省名校教研联盟高三下学期5月模拟)已知数列 是公差不为0的等差数列,其前
n项和为 , , , , 成等比数列.
(1)求 的通项公式;
(2)若 , ,求数列 的前100项和 .
【解析】(1)设数列 的首项为 ,公差为 ,
根据题意得 即
解得 或 .
又因 ,所以 .
所以 的通项公式为 .
(2)由(1)得 .
即数列 的偶数项是以4为首项,4为公差的等差数列,
奇数项是以 为首项,16为公比的等比数列.
数列 的前100项中偶数项有50项,奇数项有50项,
数列 的前100项和 .
,
学科网(北京)股份有限公司.
所以 .
(九) 为等差数列,求 前n项
若 有正有负,求 的前 项和,通常通过去绝对值,把变号与不变号的分为两部分分别求和再相加,求和时
注意对n进行讨论.
【例9】已知等差数列 的前 项和为 , 与 的等差中项为 , .
(1)求数列 的通项公式;
(2)求数列 的前 项和 .
【解析】(1)设等差数列的首项为 ,公差为 ,
由题意可知, , ,
所以 ,解得: , ,
所以 ;
(2)由(1)可知, , ,当 时, ,
所以当 时,
,
当 时,
,
,
学科网(北京)股份有限公司,
所以 .
(十)等差(比)数列,插项后求和
求解此类问题的关键是确定原数列有多少项,新数列有多少项.
【例9】已知数列 是等差数列,其前 和为 , , ,数列 满足
(1)求数列 , 的通项公式;
(2)若对数列 , ,在 与 之间插入 个2( ),组成一个新数列 ,求数列 的前83项的
和 .
【解析】(1)设公差为 ,故 ,解得 ,
故 ,
故 ,①
当 时, ,
当 时, ,②
式子①-②得, ,
即 ,
当 时, 也满足上式,故 ;
学科网(北京)股份有限公司(2)因为 ,所以在 中,从项 开始,到项 为止,
共有项数为 ,
当 时, ,当 时, ,
故数列 前 项是项 之后还有 项为2,
.
【例1】(2024届陕西省安康市高新中学高三模拟)已知数列 满足 .
(1)证明:数列 是等差数列;
(2)设 ,求 的前n项和 .
【解析】(1)证明:令 ,又 ,则有
,
又 ,所以
所以数列 是以1为首项,1为公差的等差数列
(2)由(1)知, ,
学科网(北京)股份有限公司又 ,所以 ,
所以 ,
所以
【例2】(2024届湖南省岳阳市高三下学期5月岳汨联考)已知等差数列 满足 (
),数列 是公比为3的等比数列, .
(1)求数列 和 的通项公式;
(2)数列 和 中的项由小到大组成新的数列 ,记数列 的前n项和为 ,求 .
【解析】(1) ,①, ( ),②,
得: ,
∵ 为等差数列,∴ , ,
,即 ,
∴ ,
因为数列 是公比为3的等比数列, ,
学科网(北京)股份有限公司即 ,解得: ,
所以 ;
(2)由(1)可知, , ,
且数列 和 中的项由小到大组成新的数列 ,
其中 , ,此时 ,
所以数列 中数列 有 项,数列 有 项,
,
.
【例3】(2024届福建省泉州五中高三下学期适应性监测二)已知数列 和 的各项均为正,且
, 是公比3的等比数列.数列 的前n项和 满足 .
(1)求数列 , 的通项公式;
(2)设 ,求数列 的前n项和 .
【解析】(1)由题设,当 时 或 (舍),
由 ,知 ,
两式相减得 ,
(舍)或 ,即 ,
∴数列 是首项为2,公差为2的等差数列, .
又 .
学科网(北京)股份有限公司(2)
则
当n为偶数时, ;
当n为奇数时, .
所以 .
【例4】(2024届重庆市第八中学校高三下学期5月月考)已知数列 满足 ,
.
(1)求 , , ,并求证: ;
(2)求数列 的前2n项和 .
【解析】(1) , , ,
证明: ,
,
即 , ,则 ,
学科网(北京)股份有限公司故 .
(2)由(1)可得: 且 ,
所以数列 是公比为2的等比数列,
故 ,解得: , ,
故
所以
.
【例5】将n²个实数排成n行n列的数阵形式
……
(1)当 时,若每一行每一列都构成等差数列,且 ,求该数阵中所有数的和.
(2)已知 ,且每一行构成以1为公差的等差数列,每一列构成2为公差的等差数列,求这 个数的和 ;
(3)若 且每一列均为公差为d 的等差数列,每一行均为等比数列.已知
,设 求 的值.
【解析】(1)由题意 ,且每一行都成等差数列则有
学科网(北京)股份有限公司,
,
,
设所有数之和为 ,则有 ,
又因为每一列成等差数列,故有 ,即 .
(2)设第 行的和为 ,则有 ;
又因为每一列构成以2为公差的等差数列,即有当 时,
,
即数列 构成以 为首项, 为公差的等差数列,即有
.
(3)由题意每一行均为等比数列,设第二行的公比为 ,则有 ,
又因为 ,故 .从而可得第二行的通项公式 ,
即有 ,又因为每一列均为公差为 的等差数列,且 ,
可得 ,即 ,即有 ,从而有 ,
故
.
学科网(北京)股份有限公司1.(2024届浙江省精诚联盟高三下学期适应性联考)已知等比数列 和等差数列 ,满足 ,
, , .
(1)求数列 , 的通项公式;
(2)记数列 的前 项和为 ,数列 的前 项和为 .证明: .
【解析】(1)等比数列 满足 , ,所以 单调递增,
设 的公比为 ,等差数列 的公差为 ,依题意可得 ,
解得 或 (舍去),
所以 , .
(2)由(1)可得 ,
所以
所以 ,
故 ,
学科网(北京)股份有限公司又 , ,
即 ,
所以
.
2.(2024届四川省百师联盟高三冲刺卷五)已知 为正项数列 的前 项和, 且
.
(1)求数列 的通项公式;
(2)若 ,求 的前10项和 .
【解析】(1)由题意知: ,即 ,
当 时, ,
两式相减,可得 ,
因为 ,可得 .
又因为 ,当 时, ,即 ,
解得 或 (舍去),所以 (符合),
从而 ,所以数列 表示首项为3,公差为2的等差数列.
学科网(北京)股份有限公司所以数列 的通项公式为 .
(2)由题意得 ,
所以
,
所以 .
3.(2024届浙江省杭州市高三下学期4月教学质量检测)已知等差数列 的前 项和为 ,且
.
(1)求数列 的通项公式;
(2)数列 满足 ,令 ,求证: .
【解析】(1)设等差数列 的首项为 ,公差为 .
由 ,得 ,
解得: ,所以 .
(2)由(1)知, ,
即 , , ,……, ,
利用累乘法可得:
学科网(北京)股份有限公司, 也符合上式,
所以 .
4.(2024届山西省临汾市高三第二次适应性训练)已知数列 满足
.
(1)计算 ,并求数列 的通项公式;
(2)设数列 满足 ,求数列 的前 项和 .
【解析】(1)由题可知, ,
令 , ,得 ;
令 ,得 .
由已知 ,
可得 ,
两式相减得 .
解法一:
整理得: .又 满足上式.从而 对 均成立.
学科网(北京)股份有限公司因此 为常数列,即有 ,故 .
解法二:
整理得: .又 满足上式.
故 .
即 .当 时符合上式,故 .
(2)由(1)可知 ,所以 .
因此
= .
5.(2024届陕西省咸阳市高考模拟检测三)数列 满足 , .
(1)求数列 通项公式;
(2)设 ,求数列 的前 项和 .
【解析】(1)数列 中, , ,显然 ,则 ,
数列 是首项为1,公差为1的等差数列, ,
所以数列 通项公式是 .
(2)由(1)知, ,
学科网(北京)股份有限公司当 时, , ,
当 时, ,
所以 .
6.已知等差数列 的首项为2,公差为8,在 中每相邻两项之间插入三个数,使得它们与原数列的项一
起构成一个新的等差数列 .
(1)求数列 的前 项和 ;
(2)若 , , , 是从 中抽取的若干项按原来的顺序排列组成的一个等比数列, , ,令
,求数列 的前 项和 .
【解析】(1)因为等差数列 的首项为2,公差为8,
所以 , ,
又在 中每相邻两项之间插入三个数,使得它们与原数列的项一起构成一个新的等差数列 ,设其公差
为 ,
则 , ,
所以 ,
所以 ,即数列 的通项公式为 , .
所以数列 的前 项和 .
(2)设等比数列 , , , 的公比为 ,由于 , 为等比数列的前两项,且 ,
学科网(北京)股份有限公司则 ,所以 .
由(1)知 ,所以 ,从而 ,
于是
由 ,
得 ,
所以 ,
所以
从而 .
7.已知正项数列 的前 项和为 ,且 , .
(1)求 ;
(2)在数列 的每相邻两项 之间依次插入 ,得到数列 : ,
求 的前 项和.
【解析】(1)因为 ,
所以,当 时,
所以
所以 ,
因为 ,所以 ,故 .
学科网(北京)股份有限公司当 时, 适合上式,所以 , ,
所以当 时, ,
所以
(2)(解法1)因为 ,
所以数列 : ,
设 ,
则 ,
因为 ,所以 ,
所以 的前 项由 个 与 个 组成,
所以 .
(解法2)设 ,
则 ,
因为 ,所以 ,
根据数列 的定义,知
所以 ,
所以 .
学科网(北京)股份有限公司8.已知数列 的前 项和为 ,且满足 ( ),数列 满足 .
(1)求 , 的通项公式.
(2)求数列 的前 项和 .
【解析】(1)解:当 时, ,所以 ,
因为 ,当 时,可得 ,
两式相减,得 ,
所以 ,所以 ,
又因为 ,所以 是首项为 ,公比为 的等比数列,所以 ,
所以 .
(2)解:由(1)得 ,
当 时, ,
则 ,
两式相减得
学科网(北京)股份有限公司,
所以 ,
当 时,
,
综上可知,数列 的前 项和 .
9.(2024届湖南省岳阳市高三教学质量监测三)已知等差数列 满足: ,且 , , 成等比数列.
(1)求数列 的通项公式;
(2)若等差数列 的公差不为零且数列 满足: ,求数列 的前 项和 .
【解析】(1)设数列 的公差为 ,依题意, 成等比数列,所以 ,
解得 或 ,当 时, ;当 时,
所以数列 的通项公式为 或 .
学科网(北京)股份有限公司(2)因为等差数列 的公差不为零,由(1)知 ,则
,
所以 ,
即 .
10.(2024届天津市武清区杨村第一中学高考热身练)已知数列 是正项等比数列, 是等差数列,且
,
(1)求数列 和 的通项公式;
(2) ,求数列 的前 项和.
(3) 表示不超过 的最大整数, 表示数列 的前 项和,集合 共有
4个元素,求 范围;
【解析】(1)设等比数列 的公比为 ,等差数列 的公差为 ,
因为 ,
则 ,解得 或 (舍去),
所以 ; .
学科网(北京)股份有限公司(2)因为 , ,
设 ,
,
两式相减得
,
所以 ,
当n为奇数时, ,
设
,
.
(3)由题意可知: ,
其中 ,
所以 ,
集合 ,设 ,
学科网(北京)股份有限公司则 ,
所以当 时, ,当 时, .
计算可得 , , , , ,
因为集合有4个元素, .
11.(2024届广东省江门市新会华侨中学等校二模)已知 是公差为2的等差数列,数列
的前 项和为 ,且 .
(1)求 的通项公式;
(2)求 ;
(3)[x]表示不超过 的最大整数,当 时, 是定值,求正整数 的最小值.
【解析】(1)设 ,则 .
因为 是公差为2的等差数列,所以 .
设 ,则 ,
所以 时,
.
所以 ,即 ,
又 ,满足上式,所以
学科网(北京)股份有限公司(2)(方法一)因为 ,
所以
两式相减得 .
设 ,
则 ,
两式相减得
,
则 .
所以 ,即 .
(方法二)因为 ,
所以 .
所以
学科网(北京)股份有限公司则 ,
即 .
(3)当 时, ,且 ,所以 的定值为9.
所以当 时, .
令 ,则 ,
,
所以 单调递减.
因为 ,所以 ,即正整数 的最小值为
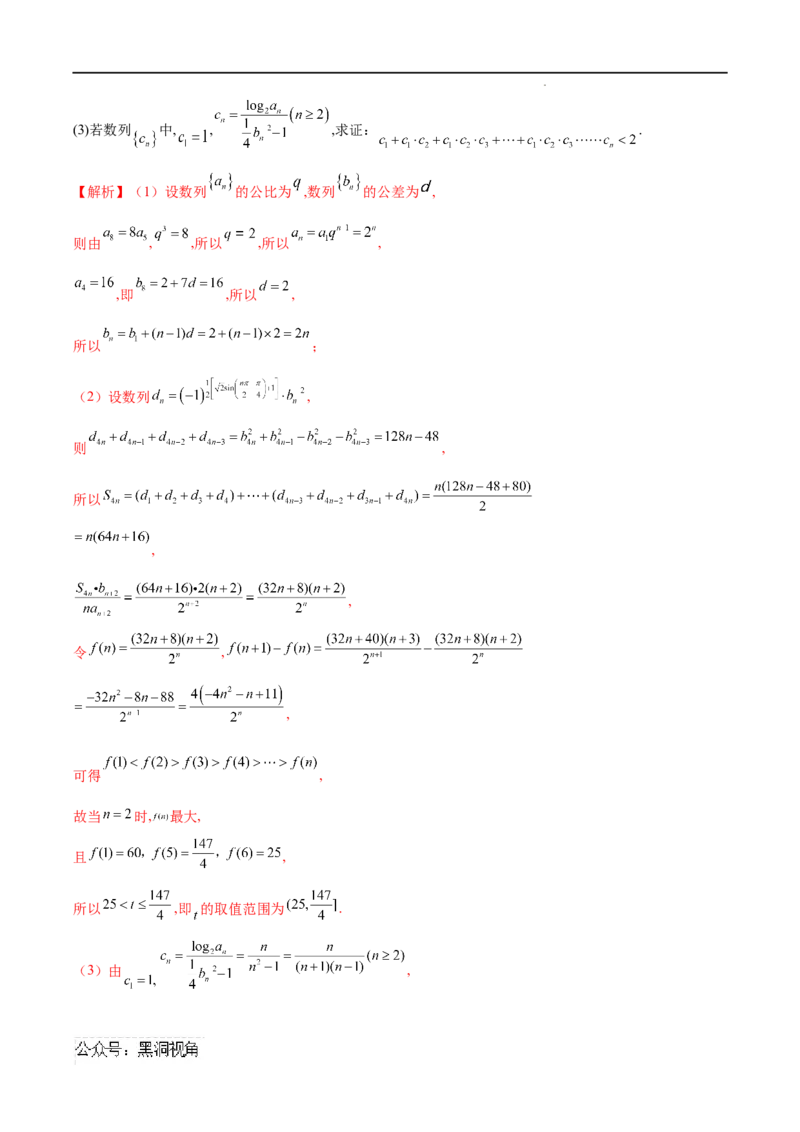
12.(2024届陕西省西安市第一中学高三下学期模拟三)已知数列 是公差不为零的等差数列,且 , ,
成等差数列, , , ( )成等比数列, .
(1)求 的值及 的通项公式;
(2)令 , ,求证: .
【解析】(1)设 的公差为 ,
∵ , , 成等差数列,∴ ,
即 ,
考虑到 ,化简得 ,即
学科网(北京)股份有限公司∴ ,∵ , , ( )成等比数列,
∴ ,即 ,
即 ,解得 .
∵ ,∴ ,解得 .
∴ ,∵ ,解得 , .
∴ .
(2)由(1)可知 ,
当 时,
所以
.
13.(2024届天津市十二区重点学校高三下学期联考二)设 是等差数列,其前 项和 , 是等比数
列,且 , , .
(1)求 与 的通项公式;
(2)设 ,求数列 的前 项和 ;
学科网(北京)股份有限公司(3)若对于任意的 不等式 恒成立,求实数 的取值范围.
【解析】(1)设等差数列 的公差为 ,等比数列 的公比为 ,
由 , ,又 , , ,
由 , ,又 , , ,
, ,
即 , .
(2)当 为奇数时, ,
记 ,则有
,
,
得:
,
,
,
当 为偶数时, ,
记 ,
,
学科网(北京)股份有限公司.
(3)由 与 恒成立,
可得 恒成立,
恒成立,即求 的最大值,
设 ,
,
单调递增,
又 ,
,
.
14.(2024届湖北省第九届高三下学期4月调研)在如图三角形数阵中,第n行有n个数, 表示第i行第j
个数,例如, 表示第4行第3个数.该数阵中每一行的第一个数从上到下构成以m为公差的等差数列,从第三
行起每一行的数从左到右构成以m为公比的等比数列 其中 已知 , ,
(1)求m及
学科网(北京)股份有限公司(2)记 除以3的余数为 , , 的前n项为 ,求
【解析】(1)由题意,可知 ,
, ,
, ,
化简整理,得 ,解得 舍去 ,或 ,
,
,
(2)
j
等于 除以3的余数.
当j为奇数时
① 时
② 时
③ 时
当j为偶数时
① 时
② 时
学科网(北京)股份有限公司③ 时
时
当 时
当 时,
综上
15.(2024届湖南省永州市高三三模)已知数列 为等比数列, 为等差数列,且 , ,
.
(1)求 , 的通项公式;
(2)数列 的前 项和为 ,集合 共有5个元素,求实数 的
取值范围;
学科网(北京)股份有限公司(3)若数列 中, , ,求证: .
【解析】(1)设数列 的公比为 ,数列 的公差为 ,
则由 , ,所以 ,所以 ,
,即 ,所以 ,
所以 ;
(2)设数列 ,
则 ,
所以
,
,
令 ,
,
可得 ,
故当 时, 最大,
且 ,
所以 ,即 的取值范围为 .
(3)由 ,
学科网(北京)股份有限公司则当 时,
,
当 时, 也满足上式,
所以 ,
,
所以原不等式成立.
16.(2024届天津市红桥区高三下学期二模)已知 是等差数列, 是公比为正数的等比数列,且 ,
, , .
(1)求数列{ , 的通项公式;
(2)设 ,
(ⅰ)求 ;
(ⅱ)求 .
【解析】(1)设 的首项为 ,公差为 , 的公比为 ,
因为 , ,
所以 ,
解得 或 (舍),
学科网(北京)股份有限公司所以 ,即 ,
所以 ,
又 , ,即 ,
解得 ,
所以 ,即
(2)(ⅰ)因为 ,则 ,
则 ;
(ⅱ)因为 ,
所以 .
学科网(北京)股份有限公司