2025年高考数学考前最后一课_2024-2025高三（6-6月题库）_2025年05月试卷_05242025年高考考前最后一课数学

{#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}以青春之名，赴梦想之约 ——致即将奔赴考场的你 亲爱的同学们： 当凤凰花开满枝头，当蝉鸣唤醒盛夏，你们将执笔为剑，在考场上书写青春的答卷。这三 年，你们见过彼此晨光熹微时的早读身影，听过自己深夜笔尖划过纸页的沙响；既有过“ 直挂 云帆济沧海” 的意气风发，也曾因“ 路漫漫其修远兮” 而彷徨。但请记住，每一滴汗水都是成 长的印记，每一次跌倒都是为腾飞蓄力。 以信念为帆，破浪前行 高考是人生的第一个重要渡口，它检验的不仅是知识，更是意志。那些挑灯夜战的夜晚、 反复演算的习题，终将凝聚成“ 天道酬勤” 的力量。无论结果如何，只要拥有梦想并为之奋 斗，你们已是自己的英雄。请带着“ 舍我其谁” 的气魄踏入考场，因为“ 自信是成功的基石， 沉着是飞翔的翅膀” 。 以坚韧为刃，披荆斩棘 学习之路从无捷径，或许你们曾因一次失利而怀疑自己，但请明白：“ 只有经历地狱般的 磨练，才能炼出创造天堂的力量。” 就像梅花经苦寒而芬芳，宝剑因磨砺而锋利。此刻，你 们只需凝神静气，将三年积淀化作笔下星河——“ 静下来，铸我实力；拼上去，亮我风采！” 以初心为灯，照亮未来 高考不是终点，而是新篇章的起点。这个世界从不会辜负认真耕耘的人，在你的笔下有一 个色彩绚丽的世界，而未来定会还你另一幅灿烂图景。愿你们像雄鹰搏击长空，如猛虎声振山 谷，在考场上“ 以平常心面对挑战，以非凡心成就自我” 。 殷殷的 嘱托 亲爱的同学们，“ 长风破浪会有时” 是你们的信念，“ 不达目的誓不罢休” 是你们的誓 言。愿你们“ 从容不迫，潇洒凯旋” ；愿你们“ 金榜题名时，言笑亦晏晏” ；更愿你们永远记 得——这场考试的意义，在于让你们发现：“ 生命中最快乐的，是拼搏而非成功；最痛苦的， 是惰性而非失败。” 希望学科网《最后一课》系列，能助你在高考的考场上擘画自己的明天！相信你们终将 “ 一举成名天下知” ，让青春的光芒照亮未来的每一步！ 学科网总经理 陈学艺 2025 年 4 月 20 日于北京 - 1 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}目 录  致2025年高考学子的一封信：以坚韧为笔，书写青春答卷 .................................................................... - 3 -  1.集合与常用逻辑用语★★★★★ .................................................................................................................. - 4 - 2.复数★★★★★ .............................................................................................................................................. - 6 - 3.基本初等函数★★★★★ .............................................................................................................................. - 8 - 4.导数★★★★★ ............................................................................................................................................ - 12 - 5.平面向量★★★★★ .................................................................................................................................... - 15 - 6.三角函数★★★★★ ................................................................................................................................... - 18 - 7.数列★★★★★ ............................................................................................................................................ - 22 - 8.立体几何★★★★★ .................................................................................................................................... - 24 - 9.直线和圆★★★★★ .................................................................................................................................... - 32 - 10.圆锥曲线★★★★★ .................................................................................................................................. - 35 - 11.计数原理★★★★★ .................................................................................................................................. - 39 - 12.概率小题★★★ ........................................................................................................................................ - 42 - 13.统计★★★★ ............................................................................................................................................. - 45 -  1.新高考数学五年考点热度大揭秘 ............................................................................................................ - 49 - 2.新高考又热起来的表面积和体积 ............................................................................................................ - 53 - 3.新高考函数压轴---抽象函数 .................................................................................................................... - 58 - 4.折展乾坤，向量破题---立体几何经典解答题 ......................................................................................... - 62 - 5.今年的19题还是新定义创新问题吗？ ................................................................................................... - 76 - 6.高考前的终极拷问：2025年考生必看！（8大必考板块150个易错问点！★） ............................. - 81 -  1.高考倒计时30天，还能干点啥提升自己呢？ ..................................................................................... - 105 - 2.高考数学核心考点解题方法与策略 ...................................................................................................... - 109 - 3.高考数学临场解题策略 .......................................................................................................................... - 116 - 4.新高考数学多项选择题的解题策略与技巧 ........................................................................................... - 120 - 5.高考数学阅卷和答题卡确注意事项 ...................................................................................................... - 125 - 6.解答题解题模型 ...................................................................................................................................... - 129 -   考前注意篇 1.考前考生需要做哪些准备 ...................................................................................................................... - 132 - 2.高考前一天需要做哪些准备 .................................................................................................................. - 134 -  考场注意篇 1.高考遇到不会的题怎么办？ .................................................................................................................. - 135 - 2.如何克服丢失不该丢的分 ...................................................................................................................... - 137 -  考后注意篇 1.高考结束后要注意什么？ ...................................................................................................................... - 139 - 2.高考志愿填报十大铁律 .......................................................................................................................... - 140 -  2025年新高考数学终极押题卷 ................................................................................................................ - 142 - 2025年新高考数学终极押题卷（解析版） ............................................................................................. - 147 - - 2 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}致 2025 年高考学子的一封信：以坚韧为笔，书写青春答卷 亲爱的同学们： 寒窗数载，今朝砺剑；山海远阔，未来可期。在你们即将踏上高考战场的时刻，请收下这 份饱含期许的祝福，愿你们以知识与信念为翼，飞向理想的星辰大海。 以“三基”为剑，破题海迷障 “基础不牢，地动山摇。”正如备考研究强调的“深化基础性考查”，高考从不是偏题怪题的 竞技场，而是扎实功底与核心素养的试金石。 筑牢知识根基：回归教材例题，梳理定理本质，如立体几何中“垂直关系”的桥梁作用，需通过 思维导图构建体系，方能以不变应万变。 规范为舟，精准为桨：谨记“答题过程的规范性”，每个步骤都是得分点；如证明题中“无 线面垂直则扣两分”，唯有严谨逻辑，方显思维光芒。 通性通法胜技巧：少一些机械刷题，多一分深度学习，正如压轴题常考的数列与导数，重 在理解通法而非套路，做到“一题一悟，触类旁通”。 以思维为帆，驭创新风浪 “运算能力决定下限，思维能力决定上限。”新高考命题趋势倡导“多思少算”，需将数学抽 象、逻辑推理化为破局利器。 跳出题海，激活思维：如函数与不等式交融题，需从几何意义或构造模型切入，而非硬算；立 体几何动态问题，可用向量法与纯几何分析双路径突破。 创新题不惧，本质为盾：若遇“新定义试题”，如“可分数列”，请冷静拆解题干，将陌生情 境转化为熟悉模型，以“转化与化归”思想拨云见日。 以心态为甲，守初心热望 高考是一场知识与心态的双重较量。考前需： 合理规划，张弛有度：45 分钟攻克选填，中档题稳扎稳打，压轴题“分段抢分”，终场前 15分钟回头检视，不留空白。 不畏失误，轻装上阵：易错点提醒的“逻辑链混乱”“坐标建系不当”，皆可成为考前自查清 单；考场上若遇阻滞，果断标记跳题，留得青山方能薪火相传。 以青春为名，赴理想之约 “教育的本质是生长，而非模仿。”高考不是终点，而是探索真理的起点。无论结果如何， 你们已在数学的对称之美、逻辑之妙中，锤炼出理性思辨的智慧与直面挑战的勇气。 愿你们合上笔盖的刹那，有侠客收剑入鞘的骄傲；愿你们拆开录取信的瞬间，有星辰大海 扑面而来的壮阔。2025的盛夏，注定因你们的拼搏而璀璨！ 谨祝： 笔下生花，圆梦今夏！ 一位与你并肩的助考者 2025年6月 - 3 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}1.集合与常用逻辑用语★★★★★ 一、近五年考情分析： 年份 题量 题号 详细知识点 20201 1 1 并集的概念及运算 20202 1 1 交集的概念及运算； 20211 1 1 交集的概念及运算； 20212 1 2 交集的概念及运算；补集的概念及运算； 20221 1 1 交集的概念及运算； 20222 1 1 交集的概念及运算；公式法解绝对值不等式； 20231 2 1 交集的概念及运算；解不含参数的一元二次不等式； 7 充要条件的证明；判断等差数列；由递推关系证明数列是等差数列； 求等差数列前n项和； 20232 1 2 根据集合的包含关系求参数； 20241 1 1 交集的概念及运算；由幂函数的单调性解不等式 20242 1 2 判断命题的真假；全称命题的否定及其真假判断； 特称命题的否定及其真假判断 此考点在每年的考试中均占据重要地位，第一题的掌握尤为关键。从考查内容来看，主要涉及交并补 运算，并常与解不等式等知识点相结合。虽然新定义的运算也可能出现，但其难度通常不高。综合历年经 验，预计命题小组对集合部分的考题进行大幅度调整的可能性较小。因此，考生应重点掌握交并补运算的 基础知识，并熟悉其与其他知识点的交汇点，以确保在考试中能够稳定得分。此外，排除法（特殊法）也 是解决此类问题的优选方法。 常见集合元素限定条件;对数不等式、指数不等式、分式不等式、一元二次不等式、绝对值不等式、 对数函数的定义域、二次根式、点集（直线、圆、方程组的解）；补集、交集和并集；不等式问题画 数轴很重要；指数形式永远大于 0 不要忽记；特别注意代表元素的字母是 x 还是 y。“充要条件”的判 断要先区分清楚条件和结论，充分性“条件⇒结论”，必要性“结论⇒条件”。要注意“三角与充要条件” 结合的考题 2025年高考预测： 1．若集合M {x∣ x 4}, N {x∣3x1}，则M  N （ ）  1   1  A． x 0 x2 B．x x2 C． x 3 x16 D．x  x16  3   3  【答案】D 1  1  【详解】M {x∣0 x16},N {x∣x }，故M N x x16 3  3  2．已知集合M {x|3x1}，N {x|1 x4}，则M N （ ） A． x 1x1 B． x x3 C．x|3x4 D． x x4 【答案】C 【详解】由题意得M N x|3x4. 3．设集合U {1,2,3,4,5,6},A{1,3,6},B{2,3,4}，则A    U B（ ） A．{3} B．{1,6} C．{5,6} D．{1,3} 【答案】B 【详解】由题设可得 B1,5,6，故A  B1,6 U U - 4 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}4．设全集U 0,1,2,4,6,8，集合M 0,4,6,N 0,1,6，则M   N （ ） U A．0,2,4,6,8 B．0,1,4,6,8 C．1,2,4,6,8 D．U 【答案】A 【详解】由题意可得 U N 2,4,8，则M  U N 0,2,4,6,8. 5．已知集合A{(x,y)|x,yN*,yx}，B{(x,y)|xy8}，则AB中元素的个数为（ ） A．2 B．3 C．4 D．6 【答案】C  y x 【详解】由题意，AB中的元素满足 ，且x,yN*，由xy82x，得x4，所以满足xy8 xy8 的有(1,7),(2,6),(3,5),(4,4)，故AB中元素的个数为4. 6．设集合A0,a，B1,a2,2a2，若AB，则a（ ）． 2 A．2 B．1 C． D．1 3 【答案】B 【详解】因为AB，则有：若a20，解得a2，此时A0,2，B1,0,2，不符合题意；若2a20， 解得a1，此时A0,1，B1,1,0，符合题意；综上所述：a1. 7．已知命题p：xR，|x1|1；命题q：x0，x3  x，则（ ） A．p和q都是真命题 B．p和q都是真命题 C．p和q都是真命题 D．p和q都是真命题 【答案】B 【详解】对于p而言，取x1，则有 x1 01，故p是假命题，p是真命题， 对于q而言，取x1，则有x3 13 1x，故q是真命题，q是假命题， 综上，p和q都是真命题. 1 8．已知命题“xR，使2x2(a1)x 0”是假命题，则实数a的取值范围是（ ） 2 A．(,1) B．(1,3) C．(3,) D．(3,1) 【答案】B 1 1 【详解】因为命题“xR，使2x2(a1)x 0”是假命题，所以2x2(a1)x 0恒成立，所以 2 2 1 Δ(a1)242 0，解得1a3，故实数a的取值范围是(1,3)． 2 9． “x为整数”是“2x1为整数”的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 【答案】A 1 【详解】当x为整数时，2x1必为整数；当2x1为整数时，x不一定为整数，例如当2x12时，x . 2 所以“x为整数”是“2x1为整数”的充分不必要条件. 10．已知aR，若集合M 1,a，N 1,0,1，则“a0”是“M N ”的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 【答案】A 【详解】当a0时，集合M 1,0，N 1,0,1，可得M N ，满足充分性，若M N ，则a0或a1， 不满足必要性，所以“a0”是“M N ”的充分不必要条件. - 5 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}2.复数★★★★★ 一、近五年考情分析： 年份 题量 题号 详细知识点 20201 1 2 复数的基本概念及除法计算； 20202 1 2 复数代数形式的乘法运算； 20211 1 2 复数代数形式的乘法运算；共轭复数的概念及计算； 20212 1 1 在各象限内点对应复数的特征；复数的除法运算； 20221 1 2 共轭复数的概念及计算； 20222 1 2 复数代数形式的乘法运算； 20231 1 2 复数的除法运算；共轭复数的概念及计算； 20232 1 1 在各象限内点对应复数的特征；复数代数形式的乘法运算； 20241 1 2 复数的乘方；复数的除法运算 20242 1 1 求复数的模 每年一题，稳得不得了，我觉得这也是送分题之一，但九省联考，不再是以选择题的方式来考， 而是放在了填空题的位置。说明考试题型有可能会变，但我认为不管怎么变，这仍然是一道送分题， 大家要细心，确保拿下。考查四则运算为主，偶尔与其他知识交汇，难度较小．考查代数运算的同时， 主要涉及考查概念有：实部、虚部、共轭复数、复数的模、对应复平面的点坐标、复数运算等.无法直 接计算时可以先设 z=a+bi。 重要提示：不管考察的是什么问题，一定要先把复数转化为标准模式 z=a+bi！ 二、2025年高考预测： 1．(22i)(12i)（ ） A．24i B．24i C．62i D．62i 【答案】D 【详解】22i12i244i2i62i 2．已知1i2 z32i，则z（ ） 3 3 3 3 A．1 i B．1 i C． i D． i 2 2 2 2 【答案】B 32i 32ii 23i 3 【详解】1i2 z2iz32i，z   1 i. 2i 2ii 2 2 3．若i(1z)1，则zz （ ） A．2 B．1 C．1 D．2 【答案】D 1 i 【详解】由题设有1z  i，故z1+i，故zz 1i1i2 i i2 4．在复平面内，13i3i对应的点位于（ ）． A．第一象限 B．第二象限 C．第三象限 D．第四象限 【答案】A 【详解】因为13i3i38i3i2 68i，则所求复数对应的点为6,8，位于第一象限. z 5．若z1 3i，则 （ ） zz 1 1 3 1 3 A．1 3i B．1 3i C．  i D．  i 3 3 3 3 【答案】C z 1 3i 1 3 【详解】z 1 3i,zz (1 3i)(1 3i)134.    i zz 1 3 3 3 - 6 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}6．在复平面内，复数z对应的点的坐标是(1, 3)，则z的共轭复数z （ ） A．1 3i B．1 3i C．1 3i D．1 3i 【答案】D 【详解】z在复平面对应的点是(1, 3)，根据复数的几何意义，z1 3i，由共轭复数的定义可知， z1 3i. 7．已知z12i，且zaz b0，其中a，b为实数，则（ ） A．a1,b2 B．a1,b2 C．a1,b2 D．a1,b2 【答案】A 【详解】z12i,zaz b12ia(12i)b(1ab)(2a2)i 由zaz b0,结合复数相等的充要条件为实部、虚部对应相等， 1ab0 a1 得 ,即 2a20 b2 3i 8．已知复数z （其中i为虚数单位），则 z （ ） 12i 5 2 A． B． C． 2 D． 5 5 2 【答案】C 3i 3i12i 32i6i 1 7 1 2 7 2 【详解】z 12i  12i12i  5  5  5 i，故 z   5    5    2. 1 9．复数 的虚部是（ ） 13i 3 1 1 3 A． B． C． D． 10 10 10 10 【答案】D 1 13i 1 3 1 3 【详解】因为z    i，所以复数z 的虚部为 . 13i (13i)(13i) 10 10 13i 10 10．（多选题）已知复数z,w均不为0，则（ ） z z2 A．z2 |z|2 B．  z |z|2 z z C．zw zw D．  w w 【答案】BCD 【详解】设z abia,bR、wcdic,dR； 对A：设z abia,bR，则z2 abi2 a22abib2 a2b22abi，  2 |z|2 a2b2 a2b2，故A错误； z z2 z z2 对B：  ，又zz z2，即有  ，故B正确； z zz z |z|2 对C：zwabicdiacbdi，则zwacbdi， zabi，wcdi，则zwabicdiacbdi， 即有zw zw，故C正确； z abi abicdi acbdadbci 对D：    w cdi cdicdi c2d2 - 7 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}acbd  2 adbc 2 a2c22abcdb2d2a2d22abcdb2c2       c2d2  c2d2   c2d22 a2c2b2d2a2d2b2c2 a2c2b2d2a2d2b2c2   ，  c2d22 c2d2 z a2b2 a2b2  c2d2  a2b2 c2d2 a2c2b2c2a2d2b2d2     ， w c2d2 c2d2 c2d2 c2d2 z z 故  ，故D正确. w w 3.基本初等函数★★★★★ 一、近五年考情分析： 年份 题量 题号 详细知识点 20201 3 8 函数奇偶性的应用；根据函数的单调性解不等式 6 对数的运算性质的应用；指数函数模型的应用（2）；利用给定函数模型解决实际问题 12 对数的运算；利用随机变量分布列的性质解题 20202 2 7 对数型复合函数的单调性； 8 函数奇偶性的应用；根据函数的单调性解不等式； 20211 2 7 求过一点的切线方程；利用导数研究函数图象及性质； 13 由奇偶性求参数； 20212 4 7 比较对数式的大小； 8 函数奇偶性的应用；函数的周期性的定义与求解； 14 函数奇偶性的定义与判断；基本初等函数的导数公式； 16 两条切线平行、垂直、重合（公切线）问题；直线的点斜式方程及辨析； 20221 3 7 比较指数幂的大小；用导数判断或证明已知函数的单调性；比较对数式的大小； 10 求在曲线上一点处的切线方程（斜率）；利用导数研究函数的零点；求极值点； 12 抽象函数的奇偶性；函数对称性的应用；函数与导函数图象之间的关系； 20222 2 8 函数奇偶性的应用；由抽象函数的周期性求函数值； 9 求在曲线上一点处的切线方程（斜率）；求正弦（型）函数的对称轴及对称中心； 利用正弦函数的对称性求参数；求sinx型三角函数的单调性； 20231 4 根据函数的单调性求参数值；判断指数型复合函数的单调性； 4 已知二次函数单调区间求参数值或范围； 10 对数的运算性质的应用；对数函数模型的应用（2）；由对数函数的单调性解不等式； 11 函数奇偶性的定义与判断；函数极值点的辨析； 15 根据函数零点的个数求参数范围；余弦函数图象的应用； 20232 3 4 函数奇偶性的应用；由奇偶性求参数； 6 由函数的单调区间求参数； 11 根据二次函数零点的分布求参数的范围；根据极值求参数； 20241 1 交集的概念及运算；由幂函数的单调性解不等式 6 判断指数函数的单调性；研究对数函数的单调性；根据分段函数的单调性求参数 5 7 正弦函数图象的应用；求函数零点或方程根的个数 8 求函数值；比较函数值的大小关系 - 8 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}13 已知切线（斜率）求参数；两条切线平行、垂直、重合（公切线）问题 20242 6 函数奇偶性的定义、判断及应用；根据函数零点的个数求参数范围；求余弦（型）函数的奇偶性 8 由对数函数的单调性解不等式；函数不等式恒成立问题 3 9 求含sinx(型)函数的值域和最值；求正弦（型）函数的最小正周期；求正弦（型）函数的对称轴 及对称中心；求函数零点或方程根的个数 牢记周期性和对称性的结论；注意单调性和奇偶性的关系；学会用特殊点巧解；隐藏性质：奇函 数在原点处有定义时， f 00；常见奇偶函数的特殊形式（总结过的）；比较大小单调性和中间变 量相结合，构造函数是底线。图像选择四部曲：定义域奇偶性特殊点单调性（求导数），特殊点最关 键。 二、2025年高考预测： 1．下列函数为增函数的是（ ） A． f x x B． f x2x C． f x x2 D． f xlog x 0.5 【答案】B x,x0 【详解】对于A，函数 f(x) x  ，函数 f(x)在(,0]上单调递减，在定义域R上不单调，A不 x,x0 是；对于B，函数 f(x)2x在R上单调递增，B是； 对于C，函数 f(x)x2在(,0]上单调递减，在定义域R上不单调，C不是； 对于D，函数 f(x)log x在(0,)上单调递减，D不是. 0.5 2．已知函数 f xlog x，则 f 9（ ） 3 A．1 B．2 C．2 D．4 【答案】C 【详解】∵ f xlog x，∴ f9log 92 3 3 3．已知函数 f(x) x3ax2,g(x)2ax2x，若函数y f(x)与y g(x)的图像有三个交点，则a的取值范 围是（ ）(,2) A． B．(2,) C．(,2)  (2,) D．(,2]  [2,) 【答案】C 【详解】因为函数y f(x)与y g(x)的图像有三个交点，所以x3ax2 2ax2x， 1 当x0时，方程必然成立，当x0时，分离参数可得a x hx，则ya与hx有两个交点，若x0， x 1 1 1 1 则hxx 2 x? 2，若x0，则hxx 2 x? 2，如图所示， x x x x 结合图像，ya要与hx有两个交点，需满足a,22,. 4．已知函数 fxln x1，记a f log π，b fln4，c fe，则（ ） 2 A．abc B．bca C．bac D．cab 【答案】D 【详解】由题可知， f x的图像关于直线x1对称，且 f x在1,上单调递减， 又log π2，且log πlog 2 2 1.5，即log π1.5,2； 2 2 2 2 - 9 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}4 4 ln41且ln41ln 1ln 1ln1.61ln 2.56 1ln e 1.5，即ln41,1.5， e 2.5 由函数的对称性知c f e f e2， 又1ln41.5log π2e2， 2 故 f e2log π f ln4，即cab 2 5．大多数居民在住宅区都会注意噪音问题.记p为实际声压，通常我们用声压级Lp（单位：分贝）来定 p 义声音的强弱，声压级Lp与声压p存在近似函数关系：Lpalg ，其中a为常数,且常数p p 0为 p 0 0 0 听觉下限阈值.若在某栋居民楼内，测得甲穿硬底鞋走路的声压p 为穿软底鞋走路的声压p 的100倍，且穿 1 2 硬底鞋走路的声压级为Lp 60分贝，恰为穿软底鞋走路的声压级Lp 的3倍.若住宅区夜间声压级超过 1 2 50分贝即扰民，该住宅区夜间不扰民情况下的声压为p，则（ ） 1 A．a20，p10 10p B．a20，p p 2 10 1 1 C．a10，p10 10p D．a10，p p 2 10 1 【答案】A p 【详解】由题意Lp Lp alg 1 alg1002a602040，得a20， 1 2 p 2 p p 则Lp20lg ，因此Lp20lg 50， p p 0 0 p LpLp 20lg 502030，则p10 10p ， 2 p 2 2 Lp Lp20lg p 1 605010，则p 10 p . 1 p 10 1 (x1)2,x0 6．已知函数 f x ，若方程 f xa有四个不同的解x,x ,x ,x ，且x x x  x ，则  log 2 x,x0 1 2 3 4 1 2 3 4 1 x x2 的取值范围是（ ） 3 4 x x x  4 1 2 3   9  7 3 9 A． , B．  2,  C．  2,  D． ,  2   4  4 2 4 【答案】D (x1)2,x0 1 【详解】因为 f x ，所以 f 01， f 21， f  1， f 21，  log 2 x,x0 2 又函数yx12对称轴为x1， 在同一平面直角坐标系中画出y f x与ya的图像， 因为方程 f xa有四个不同的解x，x ，x ，x ，且x x x  x ， 1 2 3 4 1 2 3 4 即y f x与ya有四个交点，所以0a1， 1 由图可知2x 1x 0 x 1x 2， 1 2 2 3 4 又x，x 关于x1对称，即x x 2， 1 2 1 2 1 又 x 1x 2，且log x  log x ， 2 3 4 2 3 2 4 即log x log x ，则log x log x 0， 2 3 2 4 2 3 2 4 所以log x x 0，则xx 1； 2 3 4 3 4 - 10 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}1 1 1 所以x x2 x  x  ， 3 4 x (x x ) 4 2x 4 2x 4 1 2 4 4 令g(x)x 1 ，1x2， 2x 由对勾函数的性质可知g(x)在1,2上单调递增， 3 9 3 9 1 3 9 又g1 2 ，g2 4 ，所以g(x) 2 , 4  ，即x 3 x 4 2 x (x x )  2 , 4  ． 4 1 2 7．（多选）已知实数ab0cd，则下列不等式正确的是（ ） 1 1 A．abcd B．ad bc C．ad2  bc2 D．  bc ad 【答案】BC 1 1 【详解】对于A，D，a3，b1，c1，d 7，满足ab0cd，此时abcd，  ，故A，D bc ad 错误.（判断一个结论错误时，举反例即可）对于B，ab，d c，得ad bc，故B正确. 对于C，由0cd得d2 c2 0，又ab0，所以ad2 bc2，故C正确. 8．（多选）已知实数a,b,c满足3ab1,ca,cb，则（ ） b 1 A．a2b3ab B．  a 3 b a C．  2 D．当 ac  bc 最小时，acb a b 【答案】BCD 3 【详解】对于A中，当a2,b 时，ab3，所以A错误； 2 b 1 1 1 对于B中，由3ab1，可得    ，所以B正确； a a 3 3 b b a b a 对于C中，因为 0，所以  2  2， a a b a b b a 又因为ab，所以等号不成立，  2，所以C正确； a b 对于D中，由 ac  bc 的最小值，即为数轴c到a和b的距离之和最小， 当且仅当 ac  bc  ba 时最小，此时acb，所以D正确. a 9．已知 f(x)1 是奇函数，则实数a ． e2x 1 【答案】2 a a 【详解】由题意得 f(x)f(x)，所以1 1 ，解得a2． e2x 1 e2x1 10．已知|x1|x x2|x2|m有实数解，求m的最大值为 ． 5 【答案】 4 【详解】因为|x1|x x2|x2|m，所以mx2x|x1||x2|有实数解， 令yx2x|x1||x2|，则m y ， max - 11 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#} 1 2 1 当x1时，yx2x3x  3 5；  2 4  1 2 1 当x2时，yx2x3x  3 1；  2 4  3 2 5 5 当1 x2时，yx23x1x    ；  2 4 4 5 3 5 5 5 综上所述，y ，当x 时，y  ，所以m ，则m的最大值是 . 4 2 max 4 4 4 4.导数★★★★★ 一、近五年考情分析： 考察热点 热度（2020-2024） 典型题型及特点 切线问题 ★★★★★ 求曲线在某点处的切线方程 三次函数性质 ★★★★☆ 分析极值点、零点、对称性 含参不等式恒成立 ★★★★☆ 参数范围求解 函数单调性与极值 ★★★★☆ 利用导数判断单调性、求极值 比较大小（构造函数） ★★★☆☆ 通过导数比较对数/指数式大小 抽象函数与导数综合 ★★★☆☆ 结合奇偶性、周期性等性质 零点存在性问题 ★★☆☆☆ 证明或判断零点个数 数学文化背景下的导数应用 ★★☆☆☆ 结合斐波那契数列等背景 这几年的新高考试卷中，导数出现在小题已经是一种常态，而且一出就是两题或者更多，有单独 成题，也有出现在多选题中的一个选项。考察的面很广，初等函数求导、简单复合函数的求导、切线 方程、单调性、极值点、零点等都有考察。其中重点考察了切线方程，利用导数研究函数的单调性。 二、2025年高考预测： 1．已知函数 f xcosxax在R上单调递增，则实数a的取值范围是（ ） A．,0 B．0,1 C．1, D．R 【答案】C 【详解】由题意得 fxsinxa0在R上恒成立，则asinx，因为sinx1,1，则a1. 2．设函数 f(x)在定义域内可导，y f(x)的图像如图所示，则其导函数y f(x)的图像可能是（ ） A． B． C． D． 【答案】D 【详解】由 f x的图像可知， f x在,0上为单调递减函数，故x,0时， fx0，故排除A， C；当x0,时，函数 f x的图像是先递增，再递减，最后再递增，所以 fx的值是先正，再负，最 后是正，因此排除B - 12 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}m 3．已知函数 f x m1x2是奇函数，则曲线 f x在x1处的切线的方程为（ ） x A．x y20 B．xy20 C．x y20 D．xy20 【答案】B m 【详解】由函数 f x m1x2的定义域为 x x0 ，且 f(x)是奇函数， x m m 则 f(  x)  f(x)  0，即 (m1)x2 (m1)x2 0，解得m1， x x 1 1 于是 f(x) ，求导得 f(x) ，则 f(1)1，而 f 11， x x2 所以曲线 f(x)在x1处的切线的方程为：y1x1，即xy20. 4．已知函数 f x的定义域为R，对任意xR，有 fx f x0，则“x2”是“exf x1e4f 2x3” 的（ ） A．充分不必要条件 B．必要不充分条件 C．既不充分又不必要条件 D．充要条件 【答案】A fx f x 【详解】因为 fx f x0，则 0， ex f x 令gx ，则gx0，所以gx在R上单调递增. ex f x1 f 2x3 exf x1e4f 2x3   gx1 g2x3  x12x3 x4， ex1 e2x3 所以“x2”是“exf x1exf 2x3”的充分不必要条件 5．已知实数a，b，c满足aln  2 ea  ,bln  33eb  ,clnce1，且2a13b1ce0，则（ ） A．cab B．cba C．abc D．acb 【答案】A 1 1 【详解】因为2a13b1ce0，所以a ,b ,ce， 2 3   1 1 1 因为aln 2 ea ln2 lna，所以alna ln ， 2 2 2   1 1 1 因为bln 33eb ln3 lnb，所以blnb ln ， 3 3 3 因为clnce1，所以clncelne， 1 x1 令 f xxlnx，则 fx1  x0， x x 当0x1时， fx0，当x1时， fx0， 所以函数 f x在0,1上递减，在1,上递增， 所以 f x  f 11， min 又当x0,x0时， f x，当x， f x， 由此作出函数 f x的大致图像如图所示， 1 1 1 1 因为 f a f  , f b f  , f c f e且a ,b ,ce， 2 3 2 3 则由图可知ba1,0c1， 所以cab. - 13 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}6．已知函数 f xex 2x,gxx，且 f x gx ，则x x 的最小值为（ ） 1 2 1 2 A．1 B．e C．1ln2 D．2ln2 【答案】A 【详解】由 f x gx ，得ex12x x ，化简整理得x x ex1 x ， 1 2 1 2 1 2 1 因为g（x）的值域，f（x），g（x）的定义域均为R，所以x的取值范围也是R， 1 令hxex xxR，hxex 1，令ex10，解得x0. 当x,0时，hx0，即h（x）在（-∞，0）上单调递减； 当x∞）时，hx0，即h（x）在（0，+∞）上单调递增； 所以hx h01，故x x  1. min 1 2 min 2 7．（多选）已知命题“x1,4，ex m0”为真命题，则实数m的可能取值是（ ） x A．1 B．0 C．1 D．e 【答案】AB 2 2 【详解】因为命题“x1,4，ex m0”为真命题，所以x1,4，mex  ， x x 2 2 令 f xex  ，x1,4，则 fxex  0， x x2 可知 f x为增函数，当x1时， f x有最小值 f 1e2， 故实数m的取值范围为me2 8．（多选）已知函数 f x x33ax2的极值点分别为x ,x x  x ，则下列选项正确的是（ ） 1 2 1 2 A．a0 B． f x  f x 2 1 2 C．若 f x 0，则a1 2 D．过0,2仅能做曲线y=f x的一条切线 【答案】ACD 【详解】 f x x33ax2， fx3x23a， 因为函数 f x x33ax2的极值点分别为x ,x x  x ， 1 2 1 2 所以3x23a0有两个不相等的实数根x ,x x  x ，所以a0，故A正确. 1 2 1 2 对选项B，因为a0，所以 fx3x23a3  x a  x a  ， 令 fx3  x a  x a  0，则x  a，x  a ， 1 2 所以x  , a  ， fx0， f x为增函数， x   a, a  ， fx0， f x为减函数， x  a,  ， fx0， f x为增函数， 所以x  a，x  a 为函数 f x的极值点. 1 2 - 14 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}所以 f x  f x    a 3 3a   a  2  a 3 3a a242，故B错误. 1 2 对选项C， f x   a 3 3a a2， 2 化简得：a a 1，解得a1，故C正确. 对选项D，设切点为  x ,x 33ax 2  ， fx3x23a，切线过0,2， 0 0 0 x 33ax 所以 0 0 3x 23a，即x 33ax 3x 33ax ，解得x 0， x 0 0 0 0 0 0 0 所以过0,2仅能做曲线y=f x的一条切线，故D正确. 9．曲线 f x xlnx在x1处的切线的方程为 . 【答案】xy10 【详解】 fxlnx1，∴ f11，因此切线的斜率为 f11； 又 f 10，∴f(x)在x1处的切线方程为yx1，即xy10．  π π 10．已知函数 f xae2x与gx2bsinxa x ，若曲线y f x和y gx恰有一个公切点，  2 2 a 则 的最大值是 ． b 【答案】 5 【详解】 f(x)2ae2x，g(x)2bcosx. 设公切点为(x ,y )，则 f(x )g(x )， f(x )g(x )， 0 0 0 0 0 0 ae2x0 2bsinx a 即 0 .  2ae2x0 2bcosx 0 a  5 2 5  因此 cosx 2sinx  5 cosx  sinx   5cos(x )， b 0 0  5 0 5 0 0   5 2 5 其中cos ,sin ,tan2 3， 5 5 5 2 5 因为cos ,sin ，所以为第一象限的角； 5 5 π π  π π  π π 不妨设 , ，因为x  , ，所以x  ,π ， 3 2 0  2 2 0  2 2 当且仅当x 0时，cos(x )取到最大值1， 0 0 a 所以 的最大值是 5，且x 有唯一解. b 0 5.平面向量★★★★★ 一、近五年考情分析： 年份 题量 题号 详细知识点 20201 1 7 用定义求向量的数量积 20202 1 3 向量加法的法则；向量减法的法则； 20211 1 10 逆用和、差角的余弦公式化简、求值；二倍角的余弦公式； 数量积的坐标表示；坐标计算向量的模； 20212 1 15 数量积的运算律； 20221 1 3 用基底表示向量； 20222 2 4 平面向量线性运算的坐标表示；向量夹角的坐标表示； - 15 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}10 数量积的坐标表示；已知两点求斜率；抛物线定义的理解；求直线与抛物线的交点坐标； 20231 1 3 平面向量线性运算的坐标表示；向量垂直的坐标表示；利用向量垂直求参数； 20232 2 13 数量积的运算律； 17 三角形面积公式及其应用；余弦定理解三角形；数量积的运算律； 20241 1 3 平面向量线性运算的坐标表示；向量垂直的坐标表示 20242 2 3 数量积的运算律；已知数量积求模；垂直关系的向量表示 19 由递推关系证明等比数列；求直线与双曲线的交点坐标；向量夹角的坐标表示 向量每年一题或两题，单选题4题，多选题2题，填空题2题，解答题1题，覆盖了所有的题型。考 察的比较基础,难度不大,很少与其他知识交汇,重点考查向量的基本运算。数量积问题有坐标按照坐标算       ab xx  y y ，没有坐标按照模运算ab a bcos；可以建系的建系（直角三角形、等腰、等边、矩 1 2 1 2 形、正方形、直角梯形等）、投影向量问题考的可能性不大. 几何运算注意利用三角形法则和平行四边形法则转化（注意用好作图法）；单位向量要看清，模为 1； 向量夹角为锐角，数量积大于0且向量不能同向（夹角为0）；向量夹角为钝角，数量积小于0且不能反向 （夹角为π）；两个向量不共线才可以作为基底；多个向量和差带模先平方后开方. 二、2025年高考预测： 1．已知a  m,1，b  3m1,2，若a  //b  ，则m（ ） 2 2 A．1 B．1 C． D． 3 3 【答案】A 【详解】因为a  m,1，b  3m1,2，a  //b  ，所以2m3m10，解得m1. 2．已知向量a  (2,1)，b  (2,4)，则 ab  （ ） A．2 B．3 C．4 D．5 【答案】D 【详解】因为a  b  2,12,44,3，所以 a  b   4232 5.    3．已知单位向量a，b的夹角为60°，则在下列向量中，与b垂直的是（ ） A．a  2b  B．2a  b  C．a  2b  D．2a  b  【答案】D     1 1 【详解】由已知可得：ab a  b cos60 11  . 2 2      2 1 5 A：因为(a2b)b ab2b  21 0，所以本选项不符合题意； 2 2      2 1 B：因为(2ab)b2abb 2 120，所以本选项不符合题意； 2      2 1 3 C：因为(a2b)b  ab2b  21   0，所以本选项不符合题意； 2 2      2 1 D：因为(2ab)b  2abb  2 10，所以本选项符合题意. 2 4．已知 A  B  =(2,3)，  A  C  =(3，t)，  B  C  =1，则  A  B    B  C  = A．-3 B．-2 C．2 D．3 【答案】C 【详解】由  B  C    A  C    A  B  (1,t3)，  B  C   12(t3)2 1，得t3，则  B  C  (1,0)，  AB·BC (2,3)?(1,0)21302．故选C．        5．已知a，b为单位向量，且3a5b 7，则a与ab的夹角为（ ） - 16 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}π 2π π 5π A． B． C． D． 3 3 6 6 【答案】C     【详解】因为a，b为单位向量，由3a5b 7，   2 2   2     1 所以 3a5b 499a 30ab25b 49，即930ab2549ab ， 2  1 a    a  b  2   1  设a  与  a  b夹角为，则cos     a ab   2  3 ， a ab   2  1 2 a  ab 12 1  2 π 又0,π，所以 6 6．如图，已知 A  B  a，  A  C  b  ，  B  C  4  B  D  ，C  A  3C  E  ，则  D  E  （ ） A． 3 b   1 a B． 5 b   3 a C． 3 a 1 b  D． 5 a 3 b  4 3 12 4 4 3 12 4 【答案】B    3 3    【详解】由BC4BD，得DC  BC  ACAB ，而CA3CE， 4 4 所以  D  E    D  C  C  E   3 A  C    A  B   1 C  A     3  1   A  C   3 A  B   5 b   3 a . 4 3 4 3 4 12 4 7．已知点P是  ABC的重心，则（ ）  1 1  1 1 A．AP AB AC B．AP AB AC 6 6 4 4  2 1  2 1 C．AP AC BC D．AP AB BC 3 3 3 3 【答案】D 【详解】设BC的中点为D，连接AD，点P是  ABC的重心，则P在AD上，  2 2 1  1   2 1 且AP AD  ABAC  2ABBC  AB BC 3 3 2 3 3 3 2   1 2 1  (ACCB) BC AC BC， 3 3 3 3 由此可知A，B，C错误，D正确 8．已知向量a(3,4),b  (1,0),catb  ，若 a,c  b  ,c ，则t（ ） A．6 B．5 C．5 D．6 【答案】C 93t16 3t 【详解】c3t,4,cos a,c cos b,c ,即  ,解得t5 5c c - 17 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}9．在  ABC中，点D在边AB上，BD2DA．记C  A  m，C  D  n，则C  B  （ ） A．3m2n B．2m 3n C．3m2n D．2m3n 【答案】B 【详解】因为点D在边AB上，BD2DA，所以  B  D  2  D  A  ，即C  D  C  B  2  C  A  C  D  ， 所以C  B  3C  D  2C  A  3n  2m  2m 3n． 10．设向量ax1,x,b  x,2，则（ ）     A．“x3”是“ab”的必要条件 B．“x1 3”是“a//b”的必要条件     C．“x0”是“ab”的充分条件 D．“x1 3”是“a//b”的充分条件 【答案】C     【详解】对A，当ab时，则ab0， 所以x(x1)2x0，解得x0或3，即必要性不成立，故A错误； 对C，当x0时，a  1,0,b  0,2，故a  b  0，   所以ab，即充分性成立，故C正确；   对B，当a//b时，则2(x1) x2，解得x1 3，即必要性不成立，故B错误；   对D，当x1 3时，不满足2(x1) x2，所以a//b不成立，即充分性不立，故D错误. 6.三角函数★★★★★ 一、近五年考情分析： 年份 题量 题号 详细知识点 20201 3 10 由图象确定正（余）弦型函数解析式 15 三角函数在生活中的应用 17 正弦定理解三角形；余弦定理解三角形 20202 3 11 由图象确定正（余）弦型函数解析式； 16 三角函数在生活中的应用； 17 正弦定理解三角形；余弦定理解三角形； 20211 4 4 求sinx型三角函数的单调性； 6 正、余弦齐次式的计算；二倍角的正弦公式；给值求值型问题； 10 逆用和、差角的余弦公式化简、求值；二倍角的余弦公式； 19 正弦定理边角互化的应用；几何图形中的计算； 20212 1 18 正弦定理边角互化的应用；三角形面积公式及其应用；余弦定理解三角形； 20221 2 6 由正（余）弦函数的性质确定图象（解析式）； 18 正弦定理边角互化的应用；基本不等式求和的最小值； 20222 3 6 用和、差角的余弦公式化简、求值； 9 求在曲线上一点处的切线方程（斜率）；求正弦（型）函数的对称轴及对称中心； 利用正弦函数的对称性求参数；求sinx型三角函数的单调性； 18 正弦定理解三角形；三角形面积公式及其应用；余弦定理解三角形； 20231 6 给值求值型问题；余弦定理解三角形；已知点到直线距离求参数；切线长； 4 8 用和、差角的正弦公式化简、求值；二倍角的余弦公式；给值求值型问题； 15 根据函数零点的个数求参数范围；余弦函数图象的应用； 17 用和、差角的正弦公式化简、求值；正弦定理解三角形；三角形面积公式及其应用； 20232 3 7 半角公式；二倍角的余弦公式； 16 特殊角的三角函数值；由图象确定正（余）弦型函数解析式； - 18 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}17 三角形面积公式及其应用；余弦定理解三角形；数量积的运算律； 20241 4 三角函数的化简、求值—同角三角函数基本关系；用和、差角的余弦公式化简、求值 3 7 正弦函数图象的应用；求函数零点或方程根的个数 15 已知两角的正、余弦，求和、差角的正弦；正（余）弦定理解三角形；面积公式； 20242 4 6 函数奇偶性的定义与判断；函数奇偶性的应用；根据函数零点的个数求参数范围；求余弦（型） 函数的奇偶性 9 求含sinx(型)函数的值域和最值；求正弦（型）函数的最小正周期；求正弦（型）函数的对称 轴及对称中心；求函数零点或方程根的个数 13 用和、差角的正切公式化简、求值 15 辅助角公式；正弦定理解三角形；正弦定理边角互化的应用 三角函数的定义式:会巧妙利用定义求解 sin、cos、tan,特别要注意正负;熟练诱导公式、两角和与差公 式、倍角公式、辅助角公式,符号问题太重要;牢记 sin、cos、tan 的图像性质;注意利用整体思想解决问题。   3 出现 , ,, ,2等的时候记着用诱导公式,其他角的形式用两角和与差公式展开或合并;sin2,cos2用 2 2 2 降幂公式的较多;巧妙选择倍角公式进行凑角和转化;巧妙选择两角和与差公式进行凑角和转化。 余弦定理、正弦定理、面积公式要熟记；对正余弦定理的考查主要涉及三角形的边角互化，如果是 化成角的话，下一步按三角→两角→一角进行；如果转化成边，就努力往余弦定理靠。如判断三角形的形 状等，利用正、余弦定理将条件中含有的边和角的关系转化为边或角的关系是解三角形的常规思路。三角 形内的三角函数求值、三角恒等式的证明、三角形外接圆的半径等都体现了三角函数知识与三角形知识的 交汇。 二、2025年高考预测： π 5π 1．cos2 cos2 （ ） 12 12 1 3 2 3 A． B． C． D． 2 3 2 2 【答案】D  5       3 【详解】由题意，cos2 cos2 cos2 cos2   cos2 sin2 cos  . 12 12 12  2 12 12 12 6 2 2．已知 (0,π)，且3cos28cos5，则sin（ ） 5 2 A． B． 3 3 1 5 C． D． 3 9 【答案】A 【详解】3cos28cos5，得6cos28cos80， 2 即3cos24cos40，解得cos 或cos2（舍去）， 3 5 又 (0,),sin 1cos2 .  3 3．在 ABC中，(ac)(sinAsinC)b(sinAsinB)，则C（ ）  π π 2π 5π A． B． C． D． 6 3 3 6 【答案】B 【详解】因为(ac)(sinAsinC)b(sinAsinB)， 所以由正弦定理得(ac)(ac)b(ab)，即a2c2 abb2， a2b2c2 ab 1 π 则a2b2c2 ab，故cosC    ，又0C π，所以C . 2ab 2ab 2 3 - 19 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}1  4．把函数y f(x)图像上所有点的横坐标缩短到原来的 倍，纵坐标不变，再把所得曲线向右平移 个单 2 3   位长度，得到函数ysinx 的图像，则 f(x)（ ）  4 x 7 x  A．sin   B．sin    2 12  2 12  7   C．sin2x  D．sin2x   12   12 【答案】B 1 【详解】解法一：函数y f(x)图象上所有点的横坐标缩短到原来的 倍，纵坐标不变，得到y f(2x)的 2     图像，再把所得曲线向右平移 个单位长度，应当得到y f  2x  的图像，根据已知得到了函数 3   3        ysinx 的图像，所以 f  2x  sinx ，  4   3  4   t   t  令t2x ,则x  ,x   ,  3 2 3 4 2 12  t  x  所以 f tsin  ,所以 f xsin  ； 2 12 2 12   解法二：由已知的函数ysinx 逆向变换，  4       第一步：向左平移 个单位长度，得到ysinx  sinx 的图像， 3  3 4  12 x  第二步：图象上所有点的横坐标伸长到原来的2倍，纵坐标不变，得到ysin  的图像，即为y f x 2 12 x  的图像，所以 f xsin  . 2 12 π 5．设函数 f xsinx0.已知 f x 1， f x 1，且 x x 的最小值为 ，则（ ） 1 2 1 2 2 A．1 B．2 C．3 D．4 【答案】B 【详解】由题意可知：x为 f x的最小值点，x 为 f x的最大值点， 1 2 T π 2π 则 x x   ，即T π，且0，所以 2. 1 2 min 2 2 T   6．若sin()cos()2 2cos sin，则（ ）  4 A．tan1 B．tan1 C．tan1 D．tan1 【答案】C 【详解】[方法一]：直接法 由已知得：sincoscossincoscossinsin2cossinsin, 即：sincoscossincoscossinsin0， 即：sincos0 所以tan1 故选：C [方法二]：特殊值排除法 - 20 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#} 解法一:设β=0则sinα +cosα =0，取= ，排除A, B； 4  再取α=0则sinβ +cosβ= 2sinβ，取β= ，排除D；选C. 4 [方法三]：三角恒等变换   sin()cos() 2sin（ ）= 2sin（[  ）] 4 4     2sin（ ）cos 2co（s  ）sin2 2co（s  ）sin 4 4 4   所以 2sin（ ）cos 2co（s  ）sin 4 4    sin（ ）cosco（s  ）sin=0即sin（ ）=0 4 4 4    2 2 sin（ ）=sin（）cos co（s ）sin = sin（） co（s ）=0 4 4 4 2 2 sin（）=co（s ）即tan(）=-1, cos  π 7．已知  3，则tan （ ） cossin  4 3 A．2 31 B．2 31 C． D．1 3 2 【答案】B cos 1 3 【详解】因为  3，所以  3，tan1 ， cossin 1tan 3   tan1 所以tan  2 31  4 1tan 8．在  ABC中，已知B120，AC 19，AB2，则BC（ ） A．1 B． 2 C． 5 D．3 【答案】D 【详解】设ABc,AC b,BC a，结合余弦定理：b2 a2c22accosB可得：19a2 42accos120， 即：a22a150，解得：a3（a5舍去），故BC3. π 9． ABC的内角A,B,C的对边分别为a,b,c.若b6,a2c,B ，则 ABC的面积为 .   3 【答案】6 3 1 【详解】由余弦定理得b2 a2c22accosB，所以(2c)2c222cc 62，即c2 12 2 解得c2 3,c2 3（舍去），所以a2c4 3， 1 1 3 S  acsinB 4 32 3 6 3. ABC 2 2 2  10．已知函数 f x2cosx的部分图像如图所示，则 f   . 2 【答案】 3 3 13  3 2 【详解】由题意可得： T    ,T , 2， 4 12 3 4 T - 21 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}13 13 13 当x 时，x2 2k,2k kZ， 12 12 6  令k 1可得： ， 6       5 据此有： f x2cos2x , f  2cos2  2cos  3.  6  2  2 6 6 7.数列★★★★★ 一、近五年考情分析： 等差等比用通项公式和前 n项公式，等比问题学会作比值化简；累加法、累乘法、构造法求通项， 年份 题量 题号 详细知识点 14 求等差数列前n项和 20201 2 18 求等比数列前n项和 2 15 求等差数列前n项和； 2020 18 写出等比数列的通项公式；求等比数列前n项和； 2 16 错位相减法求和；数与式中的归纳推理； 20211 17 由递推数列研究数列的有关性质；求等差数列前n项和；利用定义求等差数列通项公式； 2 12 求等比数列前n项和；数列新定义； 20212 17 等差数列通项公式的基本量计算；求等差数列前n项和；解不含参数的一元二次不等式； 1 裂项相消法求和；累乘法求数列通项；利用an与sn关系求通项或项； 20221 17 利用等差数列通项公式求数列中的项； 3 等差数列通项公式的基本量计算；已知斜率求参数； 3 等差数列通项公式的基本量计算；等比数列通项公式的基本量计算； 20222 17 数列不等式能成立（有解）问题； 22 利用导数研究不等式恒成立问题；裂项相消法求和；含参分类讨论求函数的单调区间； 7 充要条件的证明；判断等差数列；由递推关系证明数列是等差数列；求等差数列前n项和； 20231 2 20 等差数列通项公式的基本量计算；利用等差数列的性质计算；等差数列前n项和的基本量计算； 8 等比数列前n项和的基本量计算；等比数列片段和性质及应用； 20232 2 利用定义求等差数列通项公式；等差数列通项公式的基本量计算； 18 求等差数列前n项和；分组（并项）法求和； 20241 1 19 等差数列通项公式的基本量计算；数列新定义 12 等差数列通项公式的基本量计算；求等差数列前n项和 20242 2 19 由递推关系证明等比数列；求直线与双曲线的交点坐标；向量夹角的坐标表示 裂项相消、错位相减、分组求和求前 n项和要掌握类型特点。 特别注意S 和a 的关系, ,两个方向都可以转化;分组求和、裂项相消法和错位相减 n n  S ,n1 a  1 n S S ,n2 n n1 法要看清通项的形式; 等基本量的求解很重要,多解问题要多次验证进行取舍。 a，d,q,a ,S 1 n n 二、2025年高考预测： 1．等比数列a 满足a a 6，a a 24，则S （ ） n 1 2 3 4 6 A．30 B．62 C．126 D．254 【答案】C 【详解】由题意知，设等比数列的公比为q，则a a q2(a a )6q2 24，得q2 4，所以 3 4 1 2 a 5 a 6 q2(a 3 a 4 )42496，所以S 6 a 1 a 2   a 6 62496126. - 22 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}2．设等差数列{a }的前n项和为S ，若S 28，则a a a 的值为（ ） n n 7 2 3 7 A．8 B．10 C．12 D．14 【答案】C 7(a a ) 【详解】因为S 28，由等差数列的性质和求和公式得S  1 7 7a 28，即a 4， 7 7 2 4 4 则a a a 3a 9d 3(a 3d)3a 12. 2 3 7 1 1 4 a 3．记S 为非零数列a 的前n项和，若S 2S，nN*，则 4 （ ） n n n1 n a 1 A．2 B．4 C．8 D．16 【答案】B 【详解】S 2S，nN*，则S S S .即a S . n1 n n1 n n n1 n a 4a a a ,a a a 2a ， a a a a 2a 2a 4a .故 4  1 4. 2 1 3 1 2 1 4 1 2 3 1 1 1 a a 1 1 4．若正项等比数列a 满足a a 22n nN* ，则数列a 的前4项的和S 的值是（ ） n n n1 n 4 15 2 A．15 2 B． C．8 2 D．6 26 4 【答案】A 【详解】设正项等比数列a 的公比为q0， n a a 22(n1) 因为a a 22n(nN*)，所以 n1 n2  4q2， n n1 a a 22n n n1 解得q  2，所以a 2222n(a 0)， n n 2n1 21 所以 ，所以 ， a 2 2 a 2 2  2 n 1 2(124) 所以S  15 2， 4 12 所以数列a 的前4项的和S 的值为15 2. n 4 5．设等差数列a 的前n项和为S ，若a 3，a a 12，则S （ ） n n 2 3 4 9 A．75 B．78 C．81 D．84 【答案】C a d 3 【详解】因为a 3，a a 12，所以 1 ，解得a 1，d 2， 2 3 4 a 2da 3d 12 1 1 1 98 因此S 91 281． 9 2 6．记S 为等差数列a 的前n项和，若a 0，S 0，则（ ） n n 7 7 A．a a 0 B．a a 0 C．S S D．S 3a 3 6 5 8 4 7 14 9 【答案】D 7a a  【详解】 S  1 7 7a 0，a 0，又a 0，等差数列a 的公差d 0；  7 2 4 4 7 n 对于A，a 3 a 6 a 4 a 5 ，  a 4 0，d 0，a 5 符号不确定，则a 3 a 6 符号不确定，A错误；对于B，  a 5 符号不确定，a 0，a a 符号不确定，B错误； 8 5 8 对于C，  S 7 S 4 a 5 a 6 a 7 3a 6 ，又a 6 符号不确定，S 4 ,S 7 大小不确定，C错误； 14a a  对于D， S 3a  1 14 3a 7a a 3a 72a d3a 2d 11a d 0，S 3a  14 9 2 9 7 8 9 7 7 7 14 9 7．（多选）已知a 为等差数列，前n项和为S ，a 10，公差d = −2 ，则（ ） n n 1 A．S = S 4 7 - 23 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}B．当n = 6或7时，S 取得最小值 n C．数列 a  的前10项和为50 n D．当n≤2023时，a 与数列3m10（m N）共有671项互为相反数． n 【答案】ACD 【详解】对于A，等差数列{a }中，a 10，公差d 2，则a a (n1)d 2n12， n 1 n 1 S S a a a 3a 0，故A正确； 7 4 5 6 7 6 对于B，由A的结论，a 2n12，则a 0，由d = −2当n6时，a 0，a 0，当n6时，a 0， n 6 n 6 n (100)6 则当n5或6时，S 取得最大值，且其最大值为 30，B错误； n 2 对于C, a 1  a 2    a 10 a 1 a 2   a 6 a 7 a 8 a 9 a 10 S 6 2468302050,故C正确， 对于D，由n≤2023，则a a 4034， n 2023 则数列{a }中与数列{3m10}中的项互为相反数的项依次为： n 10，16，22，28，，4030， 可以组成以10为首项，6为公差的等差数列，设该数列为{c }，则c 46n， n n 若c 46n4030，解可得n671，即两个数列共有671项互为相反数，D正确． n 8．（多选）已知等差数列a 与等比数列b 的前n项和分别为S ,T ，则下列结论中正确的是（ ） n n n n A．数列  2an  是等比数列 B．T 可能为2n 1 n  S  C．数列 n 是等差数列 D．数列 b2 是等比数列 n1 n 【答案】ABD 2an1 【详解】由题设a a d为定值，则 2an1an 2d 0且为定值，A对； n1 n 2an 12n 若b 是首项为1，公比为2的等比数列，则T  2n1，B对； n n 12  S  对于数列 n ，n1时无意义，故不可能为等差数列，C错； n1 若b 的公比为q，则 b2 是首项为b2，公比为q2的等比数列，D对. n n 1 9．在正项等比数列a 中，a 48，a 12，则a  ． n 4 6 5 【答案】24 【详解】因为a 为等比数列，则a2 a a 576，且a 0，所以a 24. n 5 4 6 n 5 10．函数 f xax2bxc，若a,b,c成等比数列且 f 04，则 f x值域为 . 【答案】(,3] 【详解】由已知得， f(0)c4，由a，b，c成等比数列，则b2 ac4a，a0， 4acb2 4acac 3 所以 f(x)ax2bxc有最大值，为   c3， 4a 4a 4 所以值域为(,3]. 8.立体几何★★★★★ 一、近五年考情分析： 年份 题量 题号 详细知识点 4 球的截面的性质及计算 2020 3 16 球的截面的性质及计算 1 20 线面角的向量求法 - 24 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}4 球的截面的性质及计算； 2020 3 13 锥体体积的有关计算； 2 20 证明线面垂直；线面角的向量求法； 3 圆锥中截面的有关计算； 2021 3 12 求空间向量的数量积；空间向量的坐标表示； 1 锥体体积的有关计算；线面垂直证明线线垂直； 20 面面垂直证线面垂直；由二面角大小求线段长度或距离； 4 球的表面积的有关计算； 2021 4 5 棱台的结构特征和分类；台体体积的有关计算； 2 10 求异面直线所成的角；证明线面垂直；线面垂直证明线线垂直； 19 证明面面垂直；面面角的向量求法； 4 台体体积的有关计算； 由导数求函数的最值（不含参）；锥体体积的有关计算； 2022 8 4 球的体积的有关计算；多面体与球体内切外接问题； 1 9 求异面直线所成的角；求线面角； 19 求点面距离；面面角的向量求法； 7 球的表面积的有关计算；多面体与球体内切外接问题； 2022 3 11 锥体体积的有关计算；证明线面垂直； 2 20 证明线面平行；面面角的向量求法； 12 正棱锥及其有关计算；多面体与球体内切外接问题； 2023 3 14 台体体积的有关计算 1 18 空间位置关系的向量证明；面面角的向量求法；已知面面角求其他量； 圆锥表面积的有关计算；锥体体积的有关计算；二面角的概念及辨析；由二面角大小求线段长度 9 2023 或距离； 3 2 14 正棱台及其有关计算；锥体体积的有关计算；台体体积的有关计算； 20 证明线面垂直；线面垂直证明线线垂直；面面角的向量求法； 2024 5 圆柱表面积的有关计算；圆锥表面积的有关计算；锥体体积的有关计算 2 1 17 证明线面平行；证明面面垂直；由二面角大小求线段长度或距离 2024 7 锥体体积的有关计算；台体体积的有关计算；求线面角 2 2 17 证明线面垂直；线面垂直证明线线垂直；求平面的法向量；面面角的向量求法 新课标卷的小题主要集中在几何体的表面积和体积问题上，这一点是明确且不容忽视的。对于考 生而言，必须对此给予特别的关注。深入理解并熟练掌握空间几何体的结构特征是解答这类问题的关 键，这包括能够准确计算长度、表面积和体积等。在实践中，常采用的方法包括分割法、补体法，还 台为锥法以及等积变换法等，这些方法在处理不规则几何体体积计算时尤为有效。 此外，球与几何体的切接问题也是高考中的重要考点，通常作为客观题中的难点出现。这类问题 主要考察几何体的外接球，要求学生具备较强的空间想象能力和精确的计算能力。在选择题和填空题 中，图形通常不会直接给出，这就要求考生不仅要具备解题所需的数学技能，还需要有读题画图的能 力。 总的来说，对于空间几何体的表面积和体积问题，考生需要深入理解其结构特征，掌握相关计算 方法，并具备空间想象能力和精确的计算技巧，才能顺利应对各种考查。 二、2025年高考预测： 一、单选题 1．下列条件一定能确定一个平面的是（ ） A．空间三个点 B．空间一条直线和一个点 C．两条相互垂直的直线 D．两条相互平行的直线 - 25 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}【答案】D 【详解】由空间中不共线的三点可以确定唯一一个平面，可知A错误； 由空间中一条直线和直线外一点确定唯一一个平面，可知B错误； 两条相互垂直的直线，可能共面垂直也可能异面垂直，可知C错误； 由两条相互平行的直线能确定一个平面，可知D选项正确． 2．在正方体ABCDABCD 中，P，Q分别为BC ，BC的中点，则异面直线AQ与BP所成角的余弦值是 1 1 1 1 1 1 （ ） 1 2 1 5 A． B． C． D． 5 5 10 5 【答案】A 【详解】如图，以AB、AD、AA 分别为x、y、z轴，建立空间直角坐标系，设正方体棱长为2，则 1   A(0,0,0),B(2,0,0),P(2,1,2),Q(2,1,0)，则AQ(2,1,0),BP(0,1,2)     AQBP 1 1 因为cosAQ,BP     AQ  BP 5 5 5 1 所以异面直线AQ与BP所成角的余弦值为 . 5 3．如图，在正方体ABCDABCD 中，M ，N 分别为BC ，CD 的中点，则下列说法错误的是（ ） 1 1 1 1 1 1 A．MN与CC 垂直 B．MN与平面ACC A 垂直 1 1 1 C．MN与DC平行 D．MN与平面BDA 平行 1 【答案】C 【详解】如图，以点D为原点建立空间直角坐标系，设AB2， 则A2,0,0,B2,2,0,C0,2,0,D0,0,0,A 2,0,2,C 0,2,2, 1 1 M1,2,1,N0,1,1，   对于A，MN 1,1,0,CC 0,0,2， 1   则MNCC 0，所以MN CC ，故A正确； 1 1 对于B，  A  C  2,2,0，则M  N    A  C  0，所以MN  AC， 又AC  CC 1 C,AC,CC 1 平面ACC 1 A 1 ， 所以MN 平面ACC A ，故B正确； 1 1  对于C，DC0,2,0，   若MN与DC平行，则存在唯一实数使得DC MN ， 0  所以2，无解，所以MN与DC不平行，故C错误；  00   对于D，DB2,2,0,DA 2,0,2， 1 - 26 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#} 设平面BDA 的法向量nx,y,z， 1  n  D  B  2x2y0  则有 n  D  A  2x2z0 ，可取n1,1,1， 1   因为MNn1100，且MN 平面BDA ， 1 所以MN //平面BDA ，故D正确. 1 4．北斗卫星导航系统是中国自行研制的全球卫星导航系统．已知卫星运行轨道近似为以地球为圆心的圆形， 运行周期T 与轨道半径R之间关系为T2 KR3（K为常数）．已知甲、乙两颗卫星的运行轨道所在平面互 相垂直，甲的周期是乙的8倍，且甲的运行轨道半径为akm，A,B分别是甲、乙两颗卫星的运行轨道上的 动点，则A,B之间距离的最大值为（ ） 17 5 A． akm B． akm 4 4 3 C． akm D．5akm 2 【答案】B T  2 a 3 a 【详解】如图，设卫星乙的运行轨道半径为rkm，因为 T 甲 乙    r   ，且T 甲 8T 乙 ，所以r  4 ， 5 设地球的球心为O，则ABar a，当且仅当A,B与O共线且位于O两侧时取得等号， 4 5．三棱锥SABC中，SA平面ABC，ABBC．若该三棱锥的最长的棱长为9，最短的棱长为3，则该 三棱锥的最大体积为（ ） 9 27 A． 7 B． 3 C．18 D．36 2 2 【答案】C 【详解】因为SA平面ABC，AB,AC 平面ABC，所以SA AB，SA AC， 故SB SA2AB2,SC  SA2AC2 ， 因为ABBC，所以AC BC,AC  AB，故SBSC， 则该三棱锥的最长的棱为SC，故SC9，最短的棱为SA,AB或BC， 当最短的棱为SA，即SA3时， 由勾股定理得AC SC2SA2  819 6 2， 1 AB2BC2 故AB2BC2  AC2 72，故S  ABBC 18， ABC 2 4 当且仅当ABBC时，等号成立， - 27 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}1 1 故三棱锥体积为 S AS  18318， 3 ABC 3 当最短的棱为AB，即AB3时， 设BCx，则AC  x2 9，则SA SC2AC2  81x29  72x2 ， 1 3x 故S  ABBC  ， ABC 2 2 1 x 1 1 x272x2 三棱锥体积为 S AS  72x2  x2 72x2   18， 3 ABC 2 2 2 2 当且仅当x2 72x2，即x6时，等号成立， 当最短的棱为BC，即BC3时， 设AB x，则AC  x2 9，则SA SC2AC2  81x29  72x2 ， 1 3x 故S  ABBC  ， ABC 2 2 1 x 1 1 x272x2 三棱锥体积为 S AS  72x2  x2 72x2   18， 3 ABC 2 2 2 2 当且仅当x2 72x2，即x6时，等号成立， 综上，该三棱锥的最大体积为18. 6．已知三棱锥PABC的四个顶点都在球O的球面上，PBPC 2 5,AB AC 4，PABC2，则球O 的表面积为（ ） 316 79 158 79 A． π B． π C． π D． π 15 15 5 5 【答案】A 【详解】在三棱锥PABC中，如图，AB2PA2 20PB2，则PA AB，同理PA AC， 而AB  AC  A,AB,AC 平面ABC，因此PA平面ABC， 1 BC 15 在等腰  ABC中，ABAC4,BC2，则 cosABC  2  1，sinABC  1cos2ABC  ， 4 AB 4 1 AC 8 令 ABC的外接圆圆心为O ，则OO 平面ABC，OA   ，  1 1 1 2 sinABC 15 有OO //PA，取PA中点D，连接OD，则有OD PA，又O A平面ABC，即OAPA， 1 1 1 从而OA//OD，四边形ODAO 为平行四边形，OO  AD1，又OO OA， 1 1 1 1 1 8 79 因此球O的半径R2 OA2 OA2OO2 ( )212  ， 1 1 15 15 316 所以球O的表面积S 4πR2  π. 15 - 28 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}7．（多选）如图1，一个正四棱柱形的密闭容器水平放置，其底部镶嵌了同底的正四棱锥形实心装饰块， 容器内盛有a升水时，水面恰好经过正四棱锥的顶点P．如果将容器倒置，水面也恰好过点P（图2），则 （ ） A．若往容器内再注入a升水，则容器恰好能装满 B．正四棱锥的高等于正四棱柱高的一半 C．将容器侧面水平放置时，水面也恰好过点P D．任意摆放该容器，当水面静止时，水面都恰好经过点P 【答案】AC 【详解】设图1中水的高度h ，几何体的高为h ，底面正方形的边长为b； 2 1 2 5 则图2中水的体积为b2h b2h b2(h h )，即 b2h b2(h h )，解得h  h ， 1 2 1 2 3 2 1 2 1 3 2 所以正四棱锥的高等于正四棱柱高的一半是错误的，即B错误． 2 2 5 对于A，往容器内再注入a升水，水面将升高 h ，则h  h  h h ，容器恰好能装满，A正确； 3 2 2 3 2 3 2 1 对于C，当容器侧面水平放置时，P点在长方体中截面上，占容器内空间的一半， 所以水面也恰好经过P点，C正确； 对于D，任意摆放该容器，当水面静止时，P点在长方体中截面上，始终占容器内空间的一半，所以水面都 恰好经过点P，D正确． 对于D中，如图所示，当水面与正四棱锥的一个侧面重合时， 因为四棱锥的高为h ，几何体的高度为h ，设正四棱柱的底面边长为b， 2 1 1 AM AE AM AB 1 可得A 1 M  3 h 2 ，由  A 1 ME∽  AMB，可得 A 1 M  A 1 B ，可得A 1 E  1 AM  6 b， 1 5 1 5 5 25 所以BBECCF 的体积为V   bh b  b h b b2h ， 1 1 1 2 6 1 2 6 3 2 36 2 25 25 2 可得水的体积为V  b2h ，此时 b2h  b2h ，矛盾，所以D不正确. 1 36 2 36 2 3 2 8．（多选）在三棱锥PABC中，  PAB与  ABC均是边长为2的正三角形，O为AB的中点．若POC 120， 则（ ） A．PC  3 3 B．三棱锥PABC的体积为 2 3 7 C．三棱锥PABC的表面积为2 3 2 - 29 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}5 D．异面直线PA与BC所成角的余弦值为 8 【答案】BCD 【详解】对于A，由题意得OPOC  3,POC 120， 阿PC  OP2OC22OPOCcos120  333 3，故A错误； 对于B，因为  PAB与  ABC均是边长为2的正三角形，O为AB的中点， 所以OP AB,OC  AB， 又OPOCO,OP,OC平面OPC，所以AB平面OPC， 过点P作PM CO交CO的延长线于点M ， 因为PM 平面OPC，所以ABPM ， 又ABOCO,AB,OC平面ABC，所以PM 平面ABC， 3 则点P到平面ABC的距离为OPsin180120 ， 2 1 3 3 3 所以三棱体PABC的体积为  22  ，故B正确； 3 4 2 2 PC 2 3 2 7 对于C，在  PAC中，点A到PC的距离为 PA2   22   ，  2  2 2 1 3 1 7 3 7 所以三棱体PABC的表面积为2 22  3 2 3 ，故C正确；   2 2 2 2 2           对于D，因为PAOAOP,BC OCOB，且 PA 2, BC 2，     OA  OB 1,OP  OC  3，POC 120，POBAOC90，               所以PABC  OAOP  OCOB OAOCOAOBOPOCOPOB 5 1 3cos9011cos180 3 3cos120 31cos90 ， 2 5   所以cos  P  A  ,  B  C   PABC  2  5 ，   PA BC 22 8 5 所以异面直线PA与BC所成角的余弦值为 ，故D正确． 8 9．如图，在矩形ABCD中，AB4,AD2，点E为线段CD的中点.沿直线AE将 ADE翻折，点D运动到  点P的位置.当平面PAE与平面ABCE所成角为60时，三棱锥PABC的体积为 . 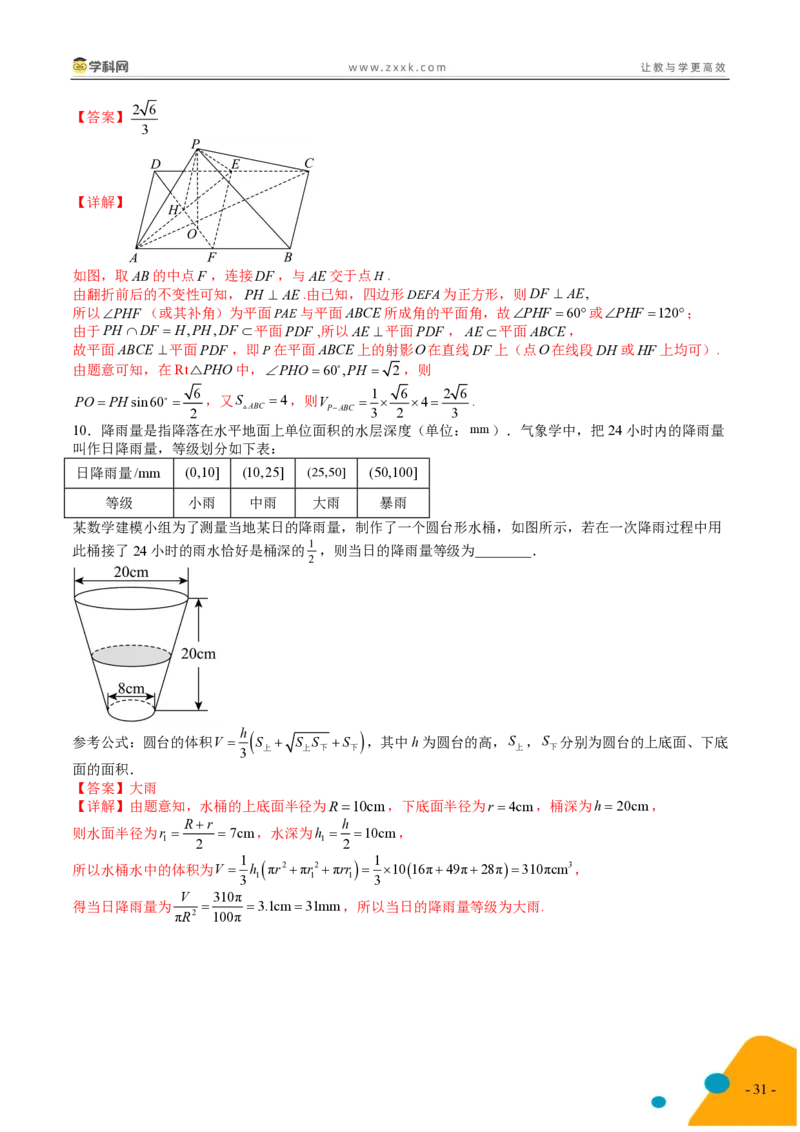- 30 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}2 6 【答案】 3 【详解】 如图，取AB的中点F ，连接DF，与AE交于点H. 由翻折前后的不变性可知，PH  AE.由已知，四边形DEFA为正方形，则DF  AE, 所以PHF（或其补角）为平面PAE与平面ABCE所成角的平面角，故PHF 60或PHF 120； 由于PH DF H,PH,DF 平面PDF ,所以AE平面PDF ，AE平面ABCE， 故平面ABCE 平面PDF ，即P在平面ABCE上的射影O在直线DF上（点O在线段DH 或HF上均可）. 由题意可知，在Rt△PHO中，PHO60,PH  2，则 6 1 6 2 6 POPHsin60  ，又S 4，则V   4 . 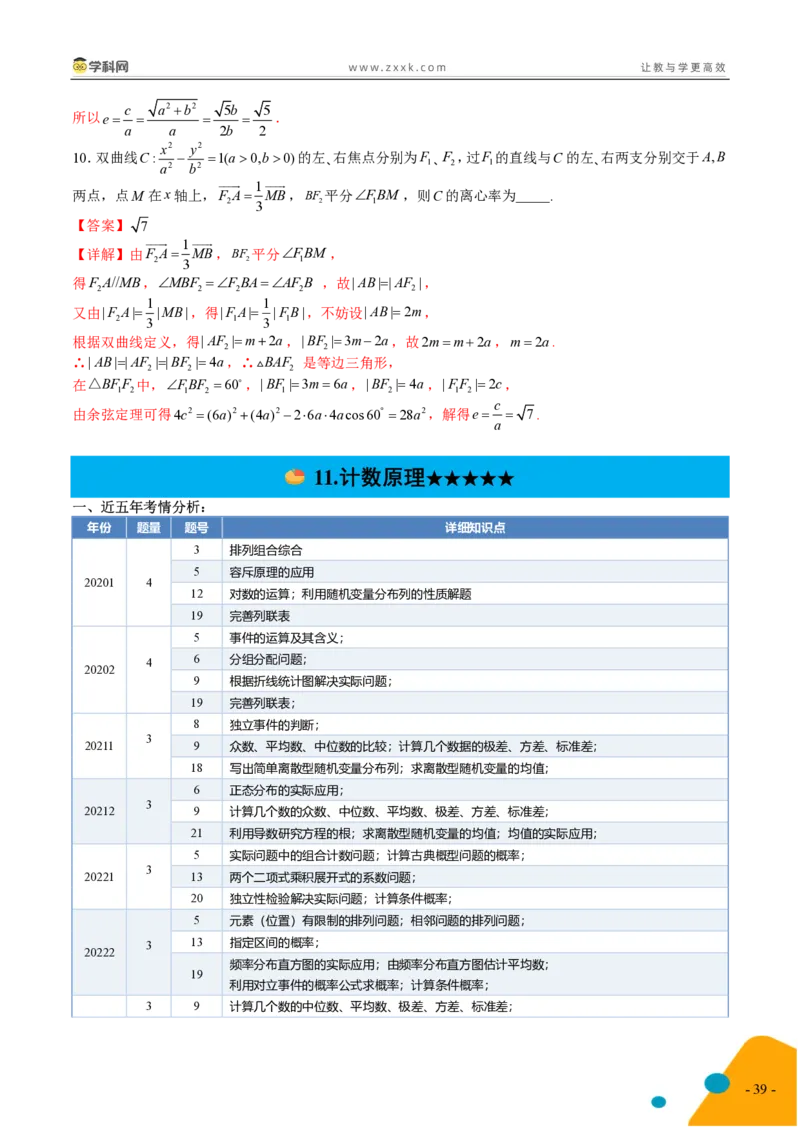2 ABC PABC 3 2 3 10．降雨量是指降落在水平地面上单位面积的水层深度（单位：mm）．气象学中，把24小时内的降雨量 叫作日降雨量，等级划分如下表： 日降雨量/mm (0,10] (10,25] (25,50] (50,100] 等级 小雨 中雨 大雨 暴雨 某数学建模小组为了测量当地某日的降雨量，制作了一个圆台形水桶，如图所示，若在一次降雨过程中用 1 此桶接了24小时的雨水恰好是桶深的 ，则当日的降雨量等级为 ． 2 h  参考公式：圆台的体积V  S  S S S ，其中h为圆台的高，S ，S 分别为圆台的上底面、下底 3 上 上 下 下 上 下 面的面积． 【答案】大雨 【详解】由题意知，水桶的上底面半径为R10cm，下底面半径为r4cm，桶深为h20cm， Rr h 则水面半径为r  7cm，水深为h  10cm， 1 2 1 2 1 1 所以水桶水中的体积为V  h  πr2πr2πrr   1016π49π28π310πcm3， 3 1 1 1 3 V 310π 得当日降雨量为  3.1cm31mm，所以当日的降雨量等级为大雨. πR2 100π - 31 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}9.直线和圆★★★★★ 一、近五年考情分析： 热点内容 热度 典型考查方式 直线与圆的位置关系 ★★★★★ 切线性质、弦长计算、距离公式应用 圆的方程与几何性质 ★★★★☆ 求圆的方程、圆心与半径、对称性 距离公式与最值问题 ★★★★ 点到直线距离、圆上点与直线距离的最值 直线斜率和倾斜角 ★★★☆ 斜率公式、倾斜角范围、两直线平行/垂直条件 对称问题 ★★★ 圆或直线关于直线对称、反射问题 代数与几何的综合应用 ★★★ 结合向量、不等式或函数最值问题 创新情境（文化/生活） ★★☆ 以实际背景（如建筑、物理）为载体的直线与圆问题 直线的考察基本上没有单独成题，而是作为一个条件或者一个选项出现在某一道题当中。我们 熟悉掌握基本知识即可。直线与圆的位置关系这几年出现的次数显著增加，值得我们重视。直线与圆 相交的弦长问题要结合点线距离和勾股定理（垂径定理）。 二、2025年高考预测：   1．已知直线 a 3 x y20的倾斜角为30，则a（ ） 4 3 2 3 A．2 3 B． C． D．0 3 3 【答案】C   3 2 3 【详解】直线 a 3 x y20的斜率为 3a，所以tan30  3a ，解得a . 3 3 2．已知直线l:x y20和圆C:x12y12 1，那么圆心C到直线l的距离是（ ） 1 A． B．1 C． 2 D．2 2 【答案】C 112 【详解】圆心为C1,1，故圆心C到直线l的距离是d   2. 2 3．已知直线l:xym0，圆C:x2y26x2y150，则“l与C有公共点”是“2 5 2m5 22” 的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 【答案】B 【详解】圆C:x2y26x2y150，即x32y12 25，圆心为C3,1，半径r =5， 31m 若l与C有公共点，则 5 ，解得25 2m25 2， 1212 所以由“l与C有公共点”推不出“25 2m5 22”，故充分性不成立； 由25 2m5 22推得出l与C有公共点，故必要性成立； 所以“l与C有公共点”是“2 5 2m5 22”的必要不充分条件. 4．已知圆C:x22xy210，直线l:xny10与圆C（ ） A．相离 B．相切 C．相交 D．相交或相切 【答案】D 【详解】根据题意，直线l的方程为l:xny10，恒过定点(0,1)， 设P为(0,1)，又由圆C:x22xy210，即(x1)2y2 2， 其圆心为(1,0)，半径r 2，由|PC|21212 2r2，则P在圆C上， - 32 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}则直线l与圆C相交或相切. 5．若点2,1在圆x2 y2x ya0的外部，则a的取值范围是（ ） 1   1  1 1  A． , B．,  C．4,  D．,4 , 2   2  2 2  【答案】C 1 【详解】依题意，方程x2 y2x ya0可以表示圆，则(1)2124a0，得a ； 2 由点2,1在圆x2 y2x ya0的外部可知：221221a0，得a4. 1 故4a . 2 6．已知P2a,0,Qb,ab(a0,b0)，动圆(xa)2(yb)2 r2(r 0)经过原点，且圆心在直线x2y2 上．当直线PQ的斜率取最大值时，r （ ） 2 2 2 3 2 3 A． B． C． D． 3 3 3 3 【答案】B ab 【详解】由题意可得，a2 b2 r2,a2b2，直线PQ的斜率为k  ． PQ 2ab 2ab 1 2 11 2 1 2b 2a 1 2b 2a  9 因为       a2b 5     52     ， ab a b 2a b 2 a b  2  a b  2 2b 2a 2 ab 2 当且仅当  ，即ab 时，等号成立，所以  ， a b 3 2ab 9 即当直线PQ的斜率取最大值时，ab 2 ，所以r2 a2b2  8 ，故r 2 2 ． 3 9 3 7．（多选）已知直线l :xay10，l :(a1)xya0，则下列说法正确的是（ ） 1 2 1 A．当a1时，直线l 的倾斜角为135 B．当l l 时，a 1 1 2 2 C．若l//l ，则a1 D．直线l 始终过定点(1,0) 1 2 1 【答案】ABD 【详解】对于A，当a1时，直线l :xy10，斜率k 1，则倾斜角为135，故A正确；对于B，l l 1 1 2 1 等价于a1a0，解得a ，故B正确； 2 1± 5 对于C，若l//l ，则a(a1)10且aa1，故a ，故C错误； 1 2 2 对于D，l :xay10，当y0时x1，所以直线l 恒过1,0，故D正确. 1 1 8．（多选）若实数x，y满足x4 y 2 xy，则下列说法正确的是（ ） A．x的最小值是4 B．x的最大值是20 C．若关于y的方程有一解，则x的取值范围为4,1620 D．若关于y的方程有两解，则x的取值范围为16,20 【答案】BD 【详解】当x0时，解得y0，符合题意；当x0时，令t y，则t0，又xy0，则t x ，即t0, x，   - 33 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}x x 则原方程可化为2t  xt2 ．设 f t2t ，gt xt2 ，t0, x，则 f t的图像是斜率为2   2 2 的直线的一部分，gt的图像是以原点为圆心，半径为 x的四分之一圆，则问题等价于 f t的图象和gt 的图像有公共点，观察图形可知， x   x   当直线与圆相切时，由 2 ，解得x  20；当直线过点 0, x 时，  x，解得x4；当直线过点 x,0  x 2 5 x 时， 2 x，解得x16．因此，要使直线与圆有公共点，则有x4,20，综上，x4,200，故x 2 的最大值为20，最小值为0．显然当x0或x 20或x4,16时，y有一解；当x16,20时，y有两解．   9．若直线l的一个方向向量d (1,1)，则l的倾斜角等于 . 3 【答案】 4 1 3 【详解】设直线l的倾斜角为，则tan 1，  0,，则 . 1 4 10．设直线l:xmy60和圆C:x2y24x4y0相交于M ，N 两点，若C  M  C  N  0，则m . 3 【答案】 4 【详解】方法一： 如图所示，由已知C:x2y24x4y0，即C:x22y22 8， 可得C2,2，半径r2 2，   又CMCN 0，所以CM CN ，即  CMN为等腰直角三角形， 2 所以圆心C到直线l得距离d  r2， 2 22m6 3 即d  2，解得m ； 1m2 4 方法二：设Mx,y ，Nx ,y ， 1 1 2 2 又M ，N 在直线l上，则M6my,y ，N6my ,y  1 1 2 2 由C:x2y24x4y0，即C:x22y22 8， x2y24x4y0 可得C2,2，联立圆与直线方程 ，得  1m2 y28m4y120， xmy60 Δ8m4 2 4  1m2 1216  m24m2  0，即m 62或m 62，   - 34 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}8m4 12 且y y  ，y y  ， 1 2 1m2 1 2 1m2 又C  M  4my,y 2，C  N  4my ,y 2，且C  M  C  N  0， 1 1 2 2 则4my 4my y 2y 2  1m2 y y 4m2y  y 200， 1 2 1 2 1 2 1 2 4m28m4 3 即12 200，解得m 1m2 4 10.圆锥曲线★★★★★ 一、近五年考情分析： 年份 题量 题号 详细知识点 9 二元二次方程表示的曲线与圆的关系；判断方程是否表示椭圆；双曲线定义的理解 20201 3 13 求直线与抛物线相交所得弦的弦长 22 根据椭圆过的点求标准方程；椭圆中存在定点满足某条件问题；椭圆中的定值问题 10 二元二次方程表示的曲线与圆的关系；判断方程是否表示椭圆；双曲线定义的理解； 3 14 求直线与抛物线相交所得弦的弦长； 20202 根据椭圆过的点求标准方程；求椭圆的切线方程；椭圆中三角形（四边形）的面积；求椭圆中 21 的最值问题； 5 基本不等式求积的最大值；椭圆定义及辨析； 4 11 切线长；直线与圆的位置关系求距离的最值； 20211 14 根据抛物线方程求焦点或准线；根据抛物线上的点求标准方程； 21 求双曲线的轨迹方程；双曲线中的定值问题； 3 已知点到直线距离求参数；根据抛物线方程求焦点或准线； 11 点与圆的位置关系求参数；判断直线与圆的位置关系； 5 20212 13 由双曲线的离心率求参数的取值范围；根据a,b,c齐次式关系求渐近线方程； 16 两条切线平行、垂直、重合（公切线）问题；直线的点斜式方程及辨析； 20 根据离心率求椭圆的标准方程；求弦长；椭圆中的直线过定点问题；根据弦长求参数； 11 根据抛物线方程求焦点或准线；判断直线与抛物线的位置关系；求弦长； 4 14 判断圆与圆的位置关系；圆的公切线方程； 20221 16 椭圆中焦点三角形的周长问题；根据离心率求椭圆的标准方程； 21 求双曲线中三角形（四边形）的面积问题；根据韦达定理求参数； 3 等差数列通项公式的基本量计算；已知斜率求参数； 10 数量积的坐标表示；已知两点求斜率；抛物线定义的理解；求直线与抛物线的交点坐标； 5 15 求点关于直线的对称点；直线关于直线对称问题；由直线与圆的位置关系求参数； 20222 16 根据弦长求参数；由弦中点求弦方程或斜率； 根据双曲线的渐近线求标准方程；求双曲线中的弦长； 21 由中点弦坐标或中点弦方程、斜率求参数；根据韦达定理求参数； 5 求椭圆的离心率或离心率的取值范围；由椭圆的离心率求参数的取值范围； 16 利用定义解决双曲线中焦点三角形问题；求双曲线的离心率或离心率的取值范围； 20231 3 由导数求函数的最值（不含参）；基本（均值）不等式的应用；求平面轨迹方程； 22 求直线与抛物线相交所得弦的弦长； 根据直线与椭圆的位置关系求参数或范围；椭圆中三角形（四边形）的面积； 20232 3 5 求椭圆中的参数及范围； - 35 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}抛物线定义的理解；根据焦点或准线写出抛物线的标准方程；求直线与抛物线的交点坐标； 10 与抛物线焦点弦有关的几何性质； 直线的点斜式方程及辨析；根据a、b、c求双曲线的标准方程；双曲线中的动点在定直线上问 21 题； 11 由方程研究曲线的性质；求平面轨迹方程 12 求双曲线的离心率或离心率的取值范围 20241 3 根据椭圆过的点求标准方程；求椭圆的离心率或离心率的取值范围； 16 椭圆中三角形（四边形）的面积；根据韦达定理求参数 5 求平面轨迹方程；轨迹问题——椭圆 20242 3 10 切线长；根据抛物线方程求焦点或准线；直线与抛物线交点相关问题 19 由递推关系证明等比数列；求直线与双曲线的交点坐标；向量夹角的坐标表示 2b2 抓牢定义与几何性质，强化直线与曲线联立，数形结合很重要。椭圆的定义、标准方程、通径 、 a 勾股定理、余弦定理、设而不求、点差法。 二、2025年高考预测： 1 1．抛物线y x2的焦点坐标为（ ） 2 1  1  A． ,0 B． ,0 8  2   1  1 C．0,  D．0,   8  2 【答案】D 1  1 【详解】由y x2可得抛物线标准方程为：x2 2y，其焦点坐标为0, . 2  2 x2 y2 2．椭圆  1的离心率为（ ） 4 9 3 2 5 6 A． B． C． D． 3 3 3 3 【答案】C c 5 【详解】由椭圆方程可知a2 9，b2 4，所以c2 a2b2 5，椭圆的离心率e  . a 3 x2 y2 3．已知方程  1表示焦点在y轴上的椭圆，则实数m的取值范围是（ ） 52m 2m1  5   1 A． ,1 B．1,   2   2  5 1  5  C． ,  D． ,  2 2  2  【答案】A x2 y2 【详解】解：方程  1表示焦点在y轴上的椭圆， 52m 2m1 5  5  则2m152m0，解得 m1，故实数m的取值范围是 ,1. 2  2  x2 y2 4．已知双曲线  1(a0,b0)的右焦点为F，若过点F且倾斜角为60的直线与双曲线的右支有且 a2 b2 只有一个交点，则此双曲线离心率的取值范围是（ ） A．(1,2] B．(1, 3] C．(2,) D．[2,) - 36 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}【答案】D b b 【详解】由题可得渐近线y x的斜率满足 tan60 3， a a 2 c b 所以离心率e  1  13 2.   a a x2 y2 5．设B是椭圆C:  1(ab0)的上顶点，若C上的任意一点P都满足|PB|2b，则C的离心率的取 a2 b2 值范围是（ ）  2  1   2  1 A．  2 ,1    B．  2 ,1   C．  0, 2   D．  0, 2   【答案】C x2 y2 【详解】设Px ,y ，由B0,b，因为 0  0 1，a2 b2c2，所以 0 0 a2 b2  y2  c2  b3 2 b4 PB2  x2y b2 a2 1 0 y b2  y    a2b2， 0 0  b2  0 b2  0 c2  c2 b3 因为b y b，当 b，即 b2 c2时，PB2 4b2，即 PB 2b，符合题意，由b2 c2可得a2 2c2， 0 c2 max max 2 即 0e ； 2 当 b3 b，即b2 c2时， PB2  b4 a2b2，即 b4 a2b2 4b2，化简得，  c2b22 0，显然该不 c2 max c2 c2 等式不成立． 4 6．过抛物线C：y2 4x的焦点F 的直线交抛物线C于A(x,y )、B(x ,y )两点，且x x  ，则弦AB的 1 1 2 2 1 2 3 长为（ ） 16 10 8 A． B．4 C． D． 3 3 3 【答案】C 【详解】抛物线的焦点弦公式为：x x  p，由抛物线方程可得：p2，则弦AB的长为 1 2 4 10 x x  p 2 . 1 2 3 3 7．（多选）在平面直角坐标系xOy中，抛物线y2 6x的焦点为F ，准线为l，P为抛物线上一点，PAl， A为垂足.若直线AF 的斜率k  3，则下列结论正确的是（ ） 3  A．准线方程为x3 B．焦点坐标F ,0 2  9  C．点P的坐标为 ,3 3 D．PF的长为3 2  【答案】BC 3  3 【详解】由抛物线方程为y2 6x，焦点坐标F ,0，准线方程为x ，A错B对； 2  2 - 37 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#} 3  直线AF 的斜率为 3，直线AF 的方程为y 3x ，  2 3  3  当x 时，y3 3，A ,3 3， 2  2   PAl，A为垂足， 9  点P的纵坐标为3 3，可得点P的坐标为 ,3 3，C对； 2  9  3 根据抛物线的定义可知|PF||PA|  6，D错. 2  2 x2 y2 8．（多选）已知椭圆C:  1(ab0)的左、右两个焦点分别是F ，F ，过点F 且斜率为k的直线l a2 b2 1 2 1 与椭圆交于A，B两点，则下列说法中正确的有（ ） A．当k 0时，△ABF 的周长为4a 2 b2 B．若AB的中点为M ，则k k  （O为坐标原点，M 与O不重合） OM a2 C．若  A  F    A  F  3  a2b2 ，则椭圆的离心率的取值范围是   5 , 2  1 2 5 3   1 D．若 AB 的最小值为3 a2b2 ，则椭圆的离心率e 2 【答案】ABD 【详解】因为弦AB过椭圆的左焦点F ，所以△ABF 的周长为 1 2 AB  AF  BF  AF  BF  AF  BF 4a，所以A正确； 2 2 1 1 2 2 x x y y  y y y y 设Ax 1 ,y 1 ，Bx 2 ,y 2 ，则M  1 2 2 , 1 2 2   ，有k OM  x 1 x 2 ，k  x 1 x 2 ，所以 1 2 1 2 y y y y y2y2 k k  1 2  1 2  1 2 ， OM x x x x x2x2 1 2 1 2 1 2 x2 y2  1  1 1, a2 b2 x2x2 y2y2 y2y2 b2 由 作差得： 1 2  1 2 0，所以 1 2  ， x 2 2  y 2 2 1, a2 b2 x 1 2x 2 2 a2 a2 b2 y2y2 b2 则有k k  1 2  ，所以B正确； OM x2x2 a2 1 2 设 FF 2c  c2 a2b2 ，  A  F  cx,y ，  A  F  cx,y ， 1 2 1 1 1 2 1 1   c2 所以AF AF  x2c2 y2  x2a22c2a22c2,a2c2， 1 2 1 1 a2 1   c  5 1 则有a22c2 3(a2b2)3c2 a2c2，可得e  , ，所以C错误； a 5 2   2b2 2b2 由过焦点的弦中垂直于x轴的弦最短，则 AB 的最小值为 ，则有 3 a2b2 3c，即 a a c 1 2a23ac2c2 0，解得a2c，所以e  ，故D正确． a 2 9．已知焦点在y轴上的双曲线C的渐近线方程为y2x，则该双曲线的离心率为 ． 5 【答案】 2 a a 【详解】因为以原点为中心，焦点在y轴上的双曲线C的渐近线方程为y x，所以 2, b b - 38 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}c a2b2 5b 5 所以e    ． a a 2b 2 x2 y2 10．双曲线C:  1(a0,b0)的左､右焦点分别为F ､F ，过F 的直线与C的左､右两支分别交于A,B a2 b2 1 2 1  1 两点，点M 在x轴上，F A MB，BF 平分FBM ，则C的离心率为 . 2 3 2 1 【答案】 7  1 【详解】由F A MB，BF 平分FBM ， 2 3 2 1 得F A//MB，MBF FBAAFB ，故|AB||AF |， 2 2 2 2 2 1 1 又由|F A| |MB|，得|FA| |FB|，不妨设|AB|2m， 2 3 1 3 1 根据双曲线定义，得|AF |m2a，|BF |3m2a，故2mm2a，m2a. 2 2 ∴|AB||AF 2 ||BF 2 |4a，∴  BAF 2 是等边三角形， 在△BFF 中，FBF 60，|BF |3m6a，|BF |4a，|FF |2c， 1 2 1 2 1 2 1 2 c 由余弦定理可得4c2 (6a)2(4a)226a4acos60 28a2，解得e  7. a 11.计数原理★★★★★ 一、近五年考情分析： 年份 题量 题号 详细知识点 3 排列组合综合 5 容斥原理的应用 20201 4 12 对数的运算；利用随机变量分布列的性质解题 19 完善列联表 5 事件的运算及其含义； 4 6 分组分配问题； 20202 9 根据折线统计图解决实际问题； 19 完善列联表； 8 独立事件的判断； 3 20211 9 众数、平均数、中位数的比较；计算几个数据的极差、方差、标准差； 18 写出简单离散型随机变量分布列；求离散型随机变量的均值； 6 正态分布的实际应用； 3 20212 9 计算几个数的众数、中位数、平均数、极差、方差、标准差； 21 利用导数研究方程的根；求离散型随机变量的均值；均值的实际应用； 5 实际问题中的组合计数问题；计算古典概型问题的概率； 3 20221 13 两个二项式乘积展开式的系数问题； 20 独立性检验解决实际问题；计算条件概率； 5 元素（位置）有限制的排列问题；相邻问题的排列问题； 3 13 指定区间的概率； 20222 频率分布直方图的实际应用；由频率分布直方图估计平均数； 19 利用对立事件的概率公式求概率；计算条件概率； 3 9 计算几个数的中位数、平均数、极差、方差、标准差； - 39 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}20231 13 分类加法计数原理；实际问题中的组合计数问题； 21 求离散型随机变量的均值；利用全概率公式求概率； 抽样比、样本总量、各层总数、总体容量的计算； 3 分步乘法计数原理及简单应用；实际问题中的组合计数问题； 20232 3 12 利用互斥事件的概率公式求概率；独立事件的乘法公式；独立重复试验的概率问题； 19 频率分布直方图的实际应用；总体百分位数的估计； 9 指定区间的概率；正态分布的实际应用 20241 2 14 计算古典概型问题的概率；求离散型随机变量的均值；均值的性质 4 计算几个数的中位数、平均数、极差、方差、标准差 20242 3 14 全排列问题；写出基本事件 18 利用对立事件的概率公式求概率；独立事件的乘法公式；求离散型随机变量的均值 排列组合考题的难度不大，无需投入过多时间（无底洞），注意掌握好基本题型，处理好分配问题， 排列问题，以及掌握好分类讨论思想即可！二项式定理“通项问题”出现较多。赋值法不要忘记。 二、2025年高考预测： 1．x3y5展开式中第3项的系数是（ ） A．90 B．-90 C．-270 D．270 【答案】A 【详解】x3y5展开式的第3项为T C2x33y2 90x3y2，故第3项系数为90， 3 5 2．某学校寒假期间安排3名教师与4名学生去北京、上海参加研学活动，每地要求至少1名教师与2名学 生，且教师甲不去上海，则分配方案有（ ） A．36种 B．24种 C．18种 D．12种 【答案】C 【详解】当教师甲与2名学生去北京时，分配方案共有C2 6（种）； 4 当教师甲与另一名教师及2名学生去北京时，分配方案共有C1C2 12（种）， 2 4 综上，分配方案共有61218（种）. 3．1至10中的质数能够组成的所有没有重复数字的整数的个数为（ ） A．4 B．12 C．24 D．64 【答案】D 【详解】1至10中的质数有2，3，5，7， 由2，3，5，7组成的没有重复数字的整数可以为一位数、两位数、三位数、四位数， 这4个数字可组成的一位数有A1 4（个）， 4 可组成的没有重复数字的两位数有A2 12（个）， 4 可组成的没有重复数字的三位数有A3 24（个）， 4 可组成的没有重复数字的四位数有A4 24（个）， 4 则1至10中的质数能够组成的所有没有重复数字的整数的个数为412242464． 4．甲、乙、丙等5人站成一排，甲乙相邻，且乙丙不相邻， 则不同排法共有（ ） A．24 种 B．36 种 C．48 种 D．72 种 【答案】B 【详解】甲乙捆绑在一起看成一个整体，与丙以外的2人全排列，有A3A2 12种， 3 2 又因为乙丙不相邻，所以把丙放入一共有3种，所以一共有12? 3  36种 C0 C1 C2 C3 C4 C5 C6 5． 6  6  6  6  6  6  6 （ ） 30 31 32 33 34 35 36 64 64 1 1 A． B． C． D． 729 729 729 729 【答案】B - 40 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}C0 C1 C2 C3 C4 C5 C6 1 0 1 1 1 2 1 3 【详解】易知 6  6  6  6  6  6  6 C016   C115   C214   C313   30 31 32 33 34 35 36 6 3 6 3 6 3 6 3 1 4 1 5 1 6  1 6  2 6 64 C412   C511   C610   1     . 6 3 6 3 6 3  3  3 729 6．为了加强“精准扶贫”，实现伟大复兴的“中国梦”，某大学派遣甲、乙、丙、丁、戊五位同学参加A、B、C 三个贫困县的调研工作，每个县至少去1人，且甲、乙两人约定去同一个贫困县，则不同的派遣方案共有 （ ） A．24 B．36 C．48 D．64 【答案】B 【详解】当按照3:1:1进行分配时，则有C1A3 18种不同的方案；当按照2:2:1进行分配，则有C2A3 18种 3 3 3 3 不同的方案.故共有36种不同的派遣方案 9  1  7．（多选）在 x 的展开式中，下列结论正确的是（ ）    x A．第6项和第7项的二项式系数相等 B．奇数项的二项式系数和为256 C．常数项为84 D．有理项有2项 【答案】BC 9  1  【详解】 x 的展开式中共有10项，由二项式系数的性质可得展开式中的第5项和第6项的二项式系    x 数相等，故A错误； 由已知可得二项式系数之和为29，且展开式中奇数项的二项式系数和与偶数项的二项式系数和相等， 所以奇数项的二项式系数和为28 256，故B正确；   1 r 9 3 r 3 展开式的通项为T Crx9r x 2 Crx 2 ,0r9,rN ，令9 r0，解得r6． r1 9 9 2   故常数项为C6 C3 84，故C正确； 9 9 有理项中x的指数为整数，故r0，2，4，6，8，故有理项有5项，故D错误． 8．若(x1)6 a 0 a 1 x1a 2 (x1)2a 3 (x1)3  a 6 (x1)6，则（ ） A．a 64 B．a a a a 365 0 0 2 4 6 C．a 12 D．a 2a 3a 4a 5a 6a 6 5 1 2 3 4 5 6 【答案】ABD 【详解】令x1，则(11)6 a ，即a 64，故A正确； 0 0 令x0，则a a a a a a a (01)6 1， 0 1 2 3 4 5 6 令x2，则a a a a a a a (21)6 729， 0 1 2 3 4 5 6 1729 则a a a a  365，故B正确； 0 2 4 6 2 (x1)6 x12 6 ，则T Ck(x1)6k(2)k，令k 1，则a C1(2)112，故C错误；   k1 6 5 6 由(x1)6 a 0 a 1 x1a 2 (x1)2a 3 (x1)3  a 6 (x1)6两边求导， 得6(x1)5 a 2a (x1)3a (x1)2 6a (x1)5， 1 2 3  6 令x0，则a 2a 3a 4a 5a 6a 6(01)5 6，故D正确. 1 2 3 4 5 6 9．若axyx y6的展开式中x5y2的系数为9，则实数a ． 【答案】1 【详解】x y6展开式的通项公式为：T Cr x6ryr，则T C1x4y2，T C2x4y2，所以axyx y6 r1 6 2 6 3 6 展开式中x5y2的系数为C2aC1 9，解得a1．（记住我教大家的方法，关键是明确取“a”和“b”的个数。 6 6 10．图中平行四边形有 个（用数字作答）. - 41 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}【答案】90 【详解】由平行四边形有两组对边分别平行相等，所以分别从四条横线中取两条和从六条斜线中取两条即 可，即C2C2 61590. 4 6 12.概率小题★★★ 一、近五年考情分析： 出现 考查热点 典型年份/卷别/题号 核心内容与特点 频率 2022全国甲卷文6/理15； 基本事件计数、枚举法，常结合排列组合或实际 古典概型 高频 2021全国甲卷理3；2024 情境（如抽卡、出场顺序等） 新课标 II卷14 中高 2022新高考 I卷20；2021 独立性检验、全概率公式的应用，强调对概率模 条件概率 频 新高考 II卷21 型的理解与转化 概率与统 2024新课标 II卷18；2023 结合二项分布、离散型随机变量（如投篮比赛、 中频 计综合 全国乙卷理19 保险理赔），考查分布列、期望及实际应用 2024新课标 I卷9；2023 利用对称性计算概率，结合生活或职业情境（如 正态分布 中频 新课标 II卷13 收入分布、产品质量） 随机事件 2020新高考 I卷19；2021 的概率与 低频 事件关系（互斥、独立）、概率加法与乘法公式 全国乙卷理8 性质 2020年部分地方卷（如北 几何概型 低频 长度、面积比计算，近年逐渐淡化 京卷） 概率题近年来在数学考试中频繁出现，凸显了概率论的重要性及对学生逻辑思维和问题解决能力 的重视。概率题主要涉及古典概型、条件概率、相互独立事件的概率和全概率公式等。古典概型要求 确定样本空间和满足条件的事件数，进而计算概率。条件概率涉及在某一事件已发生的条件下，另一 事件发生的概率。相互独立事件的概率是指多个事件互不影响，计算时可将各事件概率相乘。全概率 公式用于计算某事件在所有可能原因下的总概率，体现概率的加法原理。难度不算大，相信同学们一 定能拿得下来. 二、2025年高考预测： 1．我国古代数学名著《数书九章》中有“米谷粒分”问题：粮仓开仓收粮，有人送来米1534石，验得米内夹 谷，抽样取米一把，数得254粒内夹谷28粒.则这批米内夹谷约为（ ） A．134石 B．156石 C．169石 D．238石 【答案】C 28 14 【详解】因为254粒内夹谷28粒，所以这批米内夹谷的概率为  ， 254 127 14 所以这批米内夹谷为1534 169 127 2．甲、乙两人玩迷宫游戏，已知迷宫的入口编号为1，出口编号分别为2，3，4，5，6，7，两人从入口进 入后，他们离开的出口编号之和为8的概率为（ ） - 42 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}1 5 1 1 A． B． C． D． 6 36 12 9 【答案】B 【详解】甲、乙两人分别从6个出口中选择1个出口有6种不同的选法， 故共有6636种不同的基本事件，又他们离开的出口编号之和为8的包含的基本事件有 5 (2,6),(6,2),(3,5),(5,3),(4,4)共5个，所以他们离开的出口编号之和为8的概率为 . 36 3．设靶子上的环数取1~10这10个正整数，脱靶计为0环．某人射击一次，设事件A“中靶”，事件B“击 中环数大于5”，事件C“击中环数大于1且小于6”，事件D “击中环数大于0且小于6”，则下列关系正  确的是（ ） A．B与C互斥 B．B与C互为对立 C．A与D互为对立 D．A与D互斥 【答案】A 【详解】对于AB，事件B和C不可能同时发生，但一次射击中有可能击中环数为1，所以B与C互斥，不 对立，所以A正确，B错误，对于CD，事件A与D有可能同时发生，所以A与D既不互斥，也不对立， 所以CD错误 4．已知随机事件A，B发生的概率分别为P(A)0.5，P(B)0.4，则下列说法正确的是（ ） A．若P(AB)0.9，则A，B相互独立 B．若A，B相互独立，则PA B0.6 C．若PA B0.5，则P(AB)0.25 D．若B A，则PB A0.8 【答案】D 【详解】对于A：因为PABPAPB，所以A与B不独立，故A错误； PAB PAPB 对于B：若A，B相互独立，则PA B  PA0.5，故B错误； PB PB PAB 对于C：因为PA B ，所以PABPBPA|B0.40.50.2，故C错误； PB PAB 0.4 对于D：若B A，则PABPB0.4，所以PB A  0.8，故D正确. PA 0.5 5．江南的周庄、同里、用直、西塘、号镇、南浔古镇，并称为江南六大古镇”，是中国江南水乡风貌最具 代表的城镇，它们以其深邃的历史文化底蕴，清丽婉约的水乡古镇风貌、古朴的吴依软语民俗风情，在世 界上独树一帜，驰名中外．这六大古镇中，其中在苏州境内的有3处，某家庭计划今年暑假从这6个古镇 中挑选2个去旅游，则至少选一个苏州古镇的概率为（ ） 2 1 3 4 A． B． C． D． 5 2 4 5 【答案】D 【详解】由题意，暑假从这6个古镇中挑选2个去旅游，共有C2 15种不同的选择方式， 6 12 4 则至少选一个苏州古镇，有C1C1C2 12种不同的选择方式，所以至少选一个苏州古镇的概率为P  . 3 3 3 15 5 6．某学校高三1班至4班举办研学游活动，有4个地方可供选择，且每班只能去一个地方．设事件M “4 个班去的地方各不相同”，N “1班独自去一个地方”，则PM N（ ） 2 1 1 4 A． B． C． D． 9 4 3 9 【答案】A 【详解】1班独自去一个地方，则有4个地方可选，其余3个班只能在1班剩下的3个地方中选择，可能性为 33327种， 所以1班独自去一个地方的情况有427108种， - 43 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}24 2 因为4个班去的地方各不相同的情况有432124种，所以PM N  ． 108 9 7．（多选）下列命题中正确的是（ ）．  1 A．已知随机变量X ~ B6, ，则D3X 212  3 B．已知随机变量X ~ N  ,2 ，且PX 4PX 0，则2 C．已知一组数据：7，7，8，9，5，6，8，8，则这组数据的第30百分位数是8 D．某小组调查5名男生和5名女生的成绩，其中男生成绩的平均数为9，方差为11；女生成绩的平均数为 7，方差为8，则该10人成绩的方差为10.5 【答案】ABD  1 1 2 4 【详解】对于A，随机变量X ~ B6, ，DX6   ，则D3X 29DX12，故A正确；  3 3 3 3 对于B，随机变量X ~ N  ,2 ，且PX 4PX 0，则根据正态分布曲线的对称性可知 40 2， 2 故B正确；对于C，依题意，这组数据共8个，从小到大排列为5，6，7，7，8，8，8，9，因为830%2.4， 所以第30百分位数是7，故C错误；对于D，依题意，设5名男生为x,x ,x ，5名女生为y ,y ,y ， 1 2 5 1 2 5 1 这10名学生的平均成绩x  59578， 10 5 5 这100名学生数学成绩的方差S2  [11(98)2] [8(78)2]10.5，故D正确. 10 10 8．（多选）下列说法正确的是（ ） A．数据8，6，4，11，3，7，9，10的上四分位数为9 B．若0PC1，0PD1，且PD1PDC ，则C，D相互独立 C．某物理量的测量结果服从正态分布N  10,2 ，越大，该物理量在一次测量中在9.8,10.2的概率越大 D．若样本数据x i1,2,,5的平均数为4，x2i1,2,,5的平均数为22，则样本数据 i i 2x 1,2x 1,,2x 1，9的方差为20 1 2 5 【答案】BD 【详解】对于A选项，将数据从小到大排列为3，4，6，7，8，9，10，11，共8个数， 910 则875%6，则上四分位数为 9.5，故A错误； 2 对于B选项，  PD1PD C ，PDCPD， PCD 由条件概率公式得PD C ，得到PCDPCPD， PC 即C，D相互独立，故B正确；对于C 选项，9.8100.2，10.2100.2， 由对称性可知在9.8,10.2的概率等于在10,10.2的概率的2倍， 当越大，数据越离散，其概率越小，故C错误； 对于D选项，由样本数据x，x ，x ，x ，x 的平均数为4， 1 2 3 4 5 得x，x ，x ，x ，x ，4的平均数为4， 1 2 3 4 5 5 由x2，x2，x2，x2，x2的平均数为22，得x2 522110， 1 2 3 4 5 i i1 5 x2542442 因此x，x ，x ，x ，x ，4的方差为 i ， 1 2 3 4 5 i1 5 6  9241，2x 1 1，2x 2 1，，2x 5 +1，9的方差为4520，故D正确. 9．某市高三年级男生的身高X（单位：cm）近似服从正态分布N  175,52 ，随机选择一名本市高三年级的 同学，则P(X 170)P(175 X 180) ． - 44 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}【答案】0.5 【详解】由题意得，P(X 170) P(X 180)，所以 P(X 170)P(175 X 180)P(X 180)P(175 X 180)0.5． 1 1 10．已知随机事件A,B满足PAB ,PA ，则PB A . 3 2 2 【答案】 3 1 【详解】PB A PAB  3  2 . PA 1 3 2 13.统计★★★★ 一、近五年考情分析： 考点 热度 典型题例 用样本估计总体 高频 2024新课标Ⅱ卷4题（中位数、平均数） 概率与统计综合 高频 2021新高考Ⅰ卷8题（概率决策） 正态分布 中高频 2024新课标Ⅰ卷9题（正态分布应用） 古典概型 中频 2022全国甲卷文科15题 条件概率 中频 2022新高考Ⅰ卷20题（指标R 分析） 排列组合 中频 2024新课标Ⅱ卷14题（排列组合应用） 二项式定理 低频 2021北京卷/浙江卷 随机变量分布列 低频 2022全国乙卷理科13题 近年来，统计小题在考试中频繁出现，今年再次出现此类题目的概率极高。考察的内容涵盖了多 个方面，如频率分布表、直方图、抽样方法、样本平均数、中位数、众数、百位数、方差、标准差、 散点图、回归分析、独立性检验等。此外，还包括正相关、负相关、完全相关、相关系数、样本中心 点以及频率分布直方图和频数分布表中的平均数和中位数等概念。虽然考察的内容较多，但考试难度 并不大，主要考查学生对相关考点的基本理解。因此，希望同学们能够充分掌握这些基本概念，以免 在考试时因不熟悉基本概念而失分。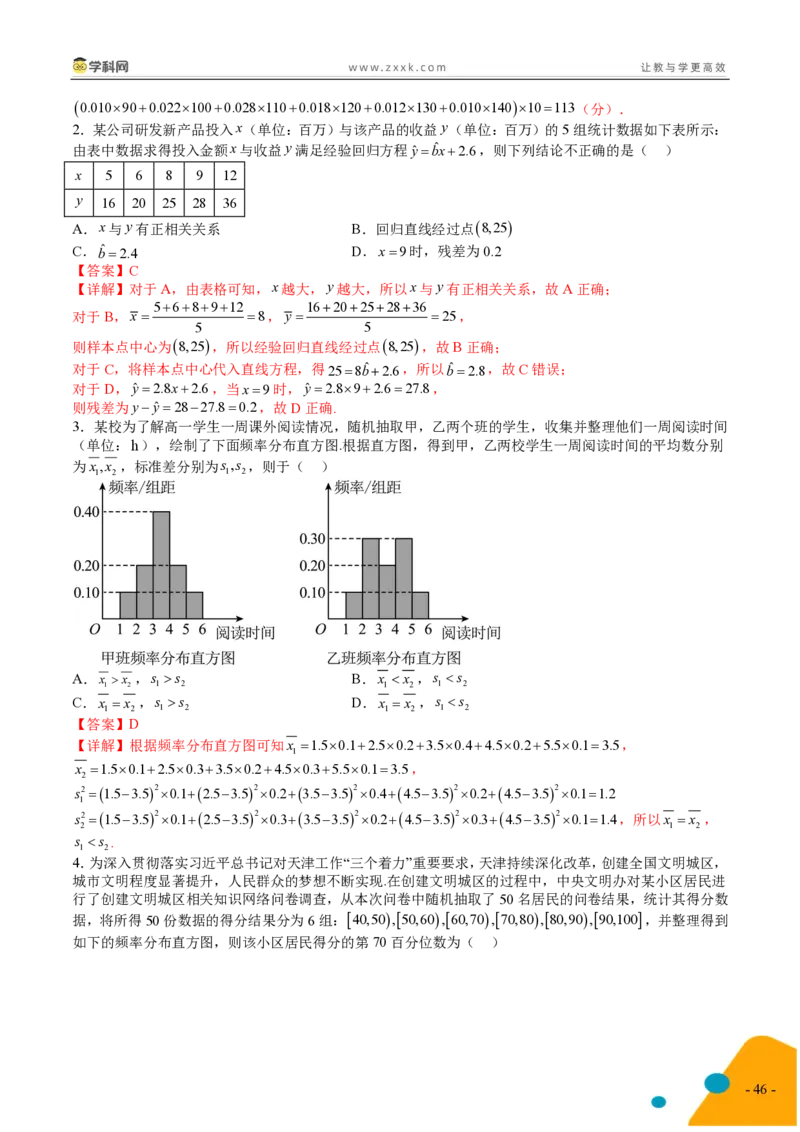 二、2025年高考预测： 1．第29届全国摄影艺术展览暨首届厦门影像艺术周在厦门举办，本届作品体现了摄影根植现实洞察思考 的魅力，显示出中国摄影人日益拓宽的视野与逐渐深化的实践．某校举行了第29届全国摄影艺术展览的参 观活动，并在活动结束后让学生对此次活动进行打分（满分150分），得到如图所示的频率分布折线图， 则估计学生对此次活动打分的平均值为（ ） A．110分 B．109分 C．113分 D．105分 【答案】C 【详解】由频率分布折线图可知0.0220.0280.0180.0122a101，解得a0.010． 故估计学生对此次活动打分的平均值为 - 45 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}0.010900.0221000.0281100.0181200.0121300.01014010113（分）． 2．某公司研发新产品投入x（单位：百万）与该产品的收益y（单位：百万）的5组统计数据如下表所示： 由表中数据求得投入金额x与收益y满足经验回归方程yˆ b ˆ x2.6，则下列结论不正确的是（ ） x 5 6 8 9 12 y 16 20 25 28 36 A．x与y有正相关关系 B．回归直线经过点8,25 C．b ˆ 2.4 D．x9时，残差为0.2 【答案】C 【详解】对于A，由表格可知，x越大，y越大，所以x与y有正相关关系，故A正确； 568912 1620252836 对于B，x  8，y  25， 5 5 则样本点中心为8,25，所以经验回归直线经过点8,25，故B正确； 对于C，将样本点中心代入直线方程，得258b ˆ 2.6，所以b ˆ 2.8，故C错误； 对于D，yˆ 2.8x2.6，当x9时，yˆ 2.892.627.8， 则残差为yyˆ 2827.80.2，故D正确. 3．某校为了解高一学生一周课外阅读情况，随机抽取甲，乙两个班的学生，收集并整理他们一周阅读时间 （单位：h），绘制了下面频率分布直方图.根据直方图，得到甲，乙两校学生一周阅读时间的平均数分别 为x,x ，标准差分别为s,s ，则于（ ） 1 2 1 2 A．x x ，s s B．x x ，s s 1 2 1 2 1 2 1 2 C．x x ，s s D．x x ，s s 1 2 1 2 1 2 1 2 【答案】D 【详解】根据频率分布直方图可知x 1.50.12.50.23.50.44.50.25.50.13.5， 1 x 1.50.12.50.33.50.24.50.35.50.13.5， 2 s2 1.53.520.12.53.520.23.53.520.44.53.520.24.53.520.11.2 1 s2 1.53.520.12.53.520.33.53.520.24.53.520.34.53.520.11.4，所以x x ， 2 1 2 s s . 1 2 4．为深入贯彻落实习近平总书记对天津工作“三个着力”重要要求，天津持续深化改革，创建全国文明城区， 城市文明程度显著提升，人民群众的梦想不断实现.在创建文明城区的过程中，中央文明办对某小区居民进 行了创建文明城区相关知识网络问卷调查，从本次问卷中随机抽取了50名居民的问卷结果，统计其得分数 据，将所得50份数据的得分结果分为6组：40,50,50,60,60,70,70,80,80,90,90,100，并整理得到 如下的频率分布直方图，则该小区居民得分的第70百分位数为（ ） - 46 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}A．89.09 B．86.52 C．84.55 D．81.32 【答案】C 【详解】由题意得0.004a0.01820.0220.028101，解得a0.006， 因为前4组数据的频率之和为0.04＋0.06＋0.220.28＝0.6， 前5组数据的频率之和为0.04＋0.06＋0.220.280.22＝0.82， 则70%分位数在80,90内，设70%分位数为x， 则0.6x800.022＝0.7，解得x84.55，所以70%分位数约为84.55． 5．假设变量x与变量Y的n对观测数据为x 1 ,y 1 ,x 2 ,y 2 ,  ,x n ,y n ，两个变量满足一元线性回归模型 Y bxe, n  .要利用成对样本数据求参数b的最小二乘估计b ˆ，即求使Q(b)y bx 2 取最小值 Ee0,De2 i i  i1 时的b的值，则（ ） n n x y x y i i i i A．b ˆ  i1 B．b ˆ  i1 n n x2 y2 i i i1 i1 n n x y x xy y i i i i C．b ˆ  i1 D．b ˆ  i1 n n n n x2y2 x x2  y y2 i i i i i1 i1 i1 i1 【答案】A n n n n n 【详解】因为Q(a,b)y bx 2  y22bx y b2x2 b2x22bx y y2， i i i i i i i i i i i1 i1 i1 i1 i1 n x y i i 上式是关于b的二次函数，因此要使Q取得最小值，当且仅当b的取值为b ˆ  i1 . n x2 i i1 6．某地为了了解学生的睡眠时间，根据初中和高中学生的人数比例采用分层抽样，抽取了40名初中生和 20名高中生，调查发现初中生每天的平均睡眠时间为8小时，方差为2，高中生每天的平均睡眠时间为7 小时，方差为1.根据调查数据，估计该地区中学生睡眠时间的总体方差约为（ ） A．1.3 B．1.5 C．1.7 D．1.9 【答案】D 40 20 23 【详解】该地区中学生每天睡眠时间的平均数为： 8 7 （小时）， 60 60 3 40   23 2 20   23 2 51 该地区中学生每天睡眠时间的方差为： 28   17   1.9. 60   3   60   3   27 7．（多选）下列可以反映总体数据集中趋势的统计特征数为（ ） A．方差 B．平均数 C．中位数 D．众数 【答案】BCD 【详解】可以反映总体数据集中趋势的统计特征数为平均数、中位数、众数； 方差反映的是总体数据的离散程度. - 47 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}8．（多选）下列命题中正确的是（ ） A．若样本数据x 1 ,x 2 ,  ,x 20 的样本方差为3，则数据2x 1 1,2x 2 1,  ,2x 20 1的方差为7 B．经验回归方程为yˆ 0.30.7x时，变量x和y负相关 C．对于随机事件A与B,PA0,PB0，若PA BPA，则事件A与B相互独立  1 D．若X B7, ，则PX k取最大值时k 4  2 【答案】BC 【详解】对于A，已知样本数据x 1 ,x 2 ,  ,x 20 的样本方差为3，则数据2x 1 1,2x 2 1,  ,2x 20 1的方差为 22312，不正确； 对于B，因为经验回归方程为yˆ 0.30.7x的斜率小于0，所以变量x和y负相关，正确； PAB 对于C，若PA BPA，根据条件概率公式有 PA，变形可得PABPAPB，则事件A PB 与B相互独立，正确；  1 1 k 1 7k 1 7 对于D，因为随机变量X ~ B7, ，所以PX kCk     Ck   ,k 0,1,2,3,4,5,6,7.  2 7 2 2 7 2 所以要使PX k最大，只需Ck,k 0,1,2,3,4,5,6,7最大，由二项式系数的性质得：当k 3或4时C3 C4 7 7 7 最大，不正确； 9．某学习兴趣小组的某学生的10次测试成绩如下：130，135，126，123，145，146，150，131，143，144， 则该学生的10次测验成绩的45百分位数是 ． 【答案】135 【详解】10个数据从小到大排序123，126，130，131，135，143，144，145，146， 150，1045%4.5，∴45百分位数是135． 10．已知a，b，c是正整数，且a[10,20]，b(20,30]，c(30,40]，当a，b，c方差最小时，写出满足条 件的一组a，b，c的值 ． 【答案】20,25,31或20,26,31（其中一组即可） abc 【详解】设x  ， 3 1 则s2  ax2bx2cx2 3   1  a2b2c23x 2 2x(abc)  3   1 1   a2b2c2 (abc)2   3 3  1  ab2bc2ca2， 9  要使方差最小，三个数据应尽量靠近，故a20，c31， 1 2 则s2  20b2 b312 31202  b251b741  ， 9  9 51 关于b的二次函数的对称轴为b ，又b(20,30]且b为正整数， 2 182 所以当b25或26时，方差s2最小，最小值为 . 9 故满足条件的a,b,c为20,25,31或20,26,31. 故答案为：20,25,31或20,26,31（其中一组即可） - 48 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}1.新高考数学五年考点热度揭秘 最近，我对五年新高考数学真题考点进行分类统计，得出了各个考点的考频。并对5年10套卷子考察 比较多的考点进行红色标注，确定为高频考点。希望这些高频考点能对大家接下来的二轮复习起到一定的 参考作用。 01.集合与常用逻辑用语 考点1集合间的基本关系(5年10卷1考) 考点2交集(5年10卷7考) 考点3并集(5年10卷1考) 考点4补集(5年10卷1考) 考点5充分条件与必要条件(5年10卷1考) 考点6全称量词与存在量词(5年10卷1考) 02:复数 考点1复数的的运算(5年10卷10考) 考点2共轭复数(5年10卷3考) 考点3复数的几何意义(5年10卷2考) 考点4复数的模(5年10卷1考) 考点5求复数的实部与虚部(5年10卷0考) 考点6复数相等(5年10卷0考) 考点7复数的分类(5年10卷0考) 03：等式与不等式综合 考点1基本不等式(5年10卷5考) 考点2解不等式(5年10卷3考) 考点3不等式的性质(5年10卷1考) 04:平面向量 考点1求平面向量数量积(10年7考) 考点2平面向量的坐标运算(5年10卷5考) 考点3平面向量垂直求参数(5年10卷3考) 考点4平面向量的基本定理及其应用(5年10卷2考) 考点5平面向量的模长(5年10卷2考) 考点6求平面向量的夹角(5年10卷2考) 考点7平面向量平行求参数(5年10卷0考) 05:三角函数 ①三角函数的图象与性质小题综合 考点1任意角和弧度制及求扇形的弧长、面积计算(5年10卷1考) 考点2任意角的三角函数(5年10卷0考) 考点3同角三角函数的基本关系(含弦切互化)(5年10卷5考) 考点4诱导公式及其化简求值(5年10卷0考) 考点5三角函数的图象与性质(5年10卷9考) 考点6三角函数的伸缩平移变换(5年10卷0考) - 49 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}②三角恒等变换与解三角形小题综合 考点1两角和与差的正弦、余弦、正切公式的应用(5年10卷4考) 考点2二倍角公式的应用(含升幂公式与降幂公式)(5年10卷3考) 考点3辅助角公式的应用(5年10卷1考) ③解三角形大题综合(5年10卷10考） 考点1求面积的值及范围或最值(5年10卷2考) 考点2求边长、周长的值及范围或最值(10年4考) 考点3求角和三角函数的值及范围或最值(5年10卷6考) 考点4求三角形的高、中线、角平分线及其他线段长(5年10卷1考) 考点5三角形中的证明问题(5年10卷3考) 06:数列 ①数列小题综合 考点1数列的增减性(5年10卷0考) 考点2递推数列及数列的通项公式(5年10卷0考) 考点3等差数列及其前n项和(5年10卷3考) 考点4等比数列及其前n项和(5年10卷1考) 考点5数列中的数学文化(5年10卷2考) 考点6数列求和(5年10卷2考) ②数列的通项公式及数列求和大题综合(5年10卷10考） 考点1等差数列的通项公式及前n项和(5年10卷4考) 考点2等比数列的通项公式及前n项和(5年10卷3考) 考点3等差等比综合(5年10卷0考) 考点4数列通项公式的构造(5年10卷3考) 考点5数列求和(5年10卷4考) 考点6数列中的不等式、最值及范围问题(5年10卷3考) 考点7数列与其他知识点的关联问题(5年10卷3考) 07:立体几何 ①立体几何的基本概念、点线面位置关系，及表面积、体积的计算小题综合 考点1点线面的位置关系及其判断(5年10卷3考) 考点2求几何体的体积(5年10卷10考) 考点3求几何体的侧面积、表面积(5年10卷2考) 考点4立体几何（球）的截面问题(5年10卷5考) ②球体的外接与内切小题综合 考点1直接求球的表面积与体积及相关应用(5年10卷3考) 考点2正方体与长方体中的球体切接问题(5年10卷1考) 考点3圆锥与圆柱中的球体切接问题(5年10卷1考) 考点4棱锥与棱台中的球体切接问题(5年10卷1考) 考点5球体切接问题中的最值及范围问题(10年5考1） ③立体几何的空间角与空间距离及其综合应用小题综合 考点1异面直线所成角及其应用(5年10卷1考) 考点2线面角及其应用(5年10卷2考) 考点3二面角及其应用(5年10卷1考) - 50 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}考点4点面距及其应用(5年10卷0考) ④立体几何大题综合(5年10卷10考) 考点1空间中的平行关系(第一问)(5年10卷3考) 考点2空间中的垂直关系(第一问)(5年10卷7考) 考点3求空间中的线段长度、点面距的值及最值或范围(5年10卷1考) 考点4求线面角及最值或范围(5年10卷2考) 考点5求二面角及最值或范围(5年10卷5考) 考点6已知异面直线所成角、线面角、二面角求值或范围(5年10卷3考) 08：计数原理与概率统计 ①排列组合与二项式定理 考点1排列组合综合(5年10卷7考) 考点2二项式定理综合(5年10卷1考) ②统计与概率小题 考点1样本的抽样方法(5年10卷1考) 考点2样本的数字特征(5年10卷3考) 考点3独立事件、积事件(5年10卷3考) 考点4正态分布指定区间的概率(5年10卷3考) 考点5图表类统计图综合(5年10卷1考) 考点6互斥事件的概率计算(5年10卷1考) 考点7古典概率(5年10卷1考) 考点8随机抽样(5年10卷0考) 考点9变量间的相关关系(5年10卷0考) 考点10条件概率(5年10卷0考) ③概率与统计大题(5年10卷10考) 考点1赛事类(分配类)的分布列及期望方差(5年10卷4考)) 考点2条件概率、全概率公式、贝叶斯公式(5年10卷3考) 考点3概率统计与其他知识的杂糅问题(5年10卷3考) 考点4独立性检验为载体及其应用(5年10卷2考) 考点5概率统计的实际应用与决策问题(5年10卷2考) 考点6求解数字样本特征及应用(5年10卷1考) 考点7线性回归直线方程为载体及其应用(5年10卷0考) 09:函数与导数 ①指数、对数、幂函数、函数图象、函数零点及函数模型的应用 考点1指数函数及其应用(5年10卷2考) 考点2对数函数及其应用(5年10卷1考) 考点3幂函数(5年10卷1考) 考点4指对幂函数值大小比较(5年10卷5考) 考点5函数图象(5年10卷0考) 考点6函数零点及其应用(5年10卷5考) 考点7函数模型(5年10卷1考) ②函数及其基本性质 考点1直接求函数值(5年10卷0考) - 51 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}考点2求函数的定义域与值域(5年10卷0考) 考点3函数单调性的判断及其应用(5年10卷8考) 考点4函数的奇偶性及其应用(5年10卷7考) 考点5函数的周期性及其应用(5年10卷2考) 考点6函数的对称性及其应用(5年10卷1考) 考点7比较大小关系(5年10卷5考) 考点8抽象函数(5年10卷7考) ③导数及其应用小题综合 考点1求切线方程及其应用(5年10卷5考) 考点2公切线问题(5年10卷1考) 考点3利用导数判断函数单调性及其应用(5年10卷2考) 考点4求极值与最值及其应用(5年10卷5考) ④导数及其应用大题综合(5年10卷10考) 考点1切线方程及其应用(5年10卷2考) 考点2具体函数及含参函数的单调性(5年10卷5考) 考点3极值最值及其应用(5年10卷3考) 考点4证明不等式(10年3考) 考点5恒成立与能成立(有解)问题(5年10卷2考) 考点6零点问题(5年10卷2考) 10:平面几何 ①直线与圆小题综合 考点1直线方程与圆的方程(5年10卷1考) 考点2直线与圆的位置关系及其应用(5年10卷2考) 考点3圆中的切线问题(10年3考) 考点4直线与圆中的最值及范围问题(5年10卷1考) ②圆锥曲线小题综合 考点1椭圆方程及其性质(5年10卷2考) 考点2双曲线方程及其性质(5年10卷2考) 考点3抛物线方程及其性质(5年10卷7考) 考点4椭圆的离心率及其应用(5年10卷2考) 考点5双曲线的离心率及其应用(5年10卷1考) 考点6直线与圆锥曲线的位置关系及其应用(5年10卷3考) 考点7曲线方程及曲线轨迹(5年10卷1考) 考点8圆锥曲线中的最值及范围问题(5年10卷1考) ③圆锥曲线大题(5年10卷10考) 考点1求轨迹方程(5年10卷7考) 考点2求斜率值或范围(5年10卷6考) 考点3离心率求值或范围综合(5年10卷3考) 考点4弦长类求值或范围综合(5年10卷2考) 考点5定值定点定直线问题(5年10卷3考) 考点6其他证明综合(5年10卷3考) 考点7圆锥曲线与其他知识点杂糅问题(5年10卷1考) - 52 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}2.体积、表面积与空间几何体全攻略 一、考情分析 1. 考查内容覆盖广泛 新高考全国卷的简单几何体考察主要集中在棱柱、棱锥、棱台、圆柱、圆锥、圆台和球等几何体的表面积 与体积计算上。这些考点几乎涵盖了所有常见的简单几何体，体现了对基础知识的全面考查。 2. 题型多样化 试卷中涉及的题型包括选择题、填空题和解答题。其中，选择题和填空题多为基础性问题，主要考查公式 的记忆和应用；解答题则通常要求考生进行较为复杂的计算或推导，考查逻辑推理和综合运用能力。 3. 难度逐年变化 从2020年至2024年，简单几何体的考查难度逐渐增加。2020年和2021年的题目相对简单，主要集中在基 础公式的直接应用；而2022年及之后的试卷中，题目开始引入更多的情境化问题，要求考生在实际应用中 进行建模和推理，难度有所提升。 4. 情境化考查 近年来，试题设置越来越注重与实际生活的结合。例如，涉及水库体积计算、建筑物的几何体积等实际问 题，考生需要在理解几何体特性的基础上，进行合理的数学建模和计算。 5. 知识交叉与综合能力考查 新高考卷在简单几何体的考查中，越来越多地融合了其他数学知识，如空间向量、平面几何等，体现了对 学生综合能力的要求。考生不仅需要掌握几何体的基本性质，还须具备一定的逻辑推理能力和空间想象能 力。 二、解答空间几何体表面积与体积问题的基本方法 1. 空间几何体表面积的求法 ①旋转体的表面积问题注意其侧面展开图的应用． ②多面体的表面积是各个面的面积之和；组合体的表面积注意衔接部分的处理． 2. 空间几何体体积问题的常见类型及解题策略 ①直接利用公式进行求解． ②用转换法、分割法、补形法等方法进行求解． 三、核心考点 考点 1 柱、锥、台的表面积 Ⅰ、柱、锥、台的表面积： S S S 表面积 侧面积 底面积 Ⅱ、圆柱的表面积 ①圆柱的侧面积：圆柱的侧面展开图是一个矩形，如下图，圆柱的底面半径为 r，母线长l，那么这个 矩形的长等于圆柱底面周长C=2πr，宽等于圆柱侧面的母线长l（也是高），由此可得S 圆柱侧 =Cl=2πrl． - 53 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}②圆柱的表面积： ． S 2r2 2rl 2r(rl) 圆柱表 Ⅲ、圆锥的表面积 ①圆锥的侧面积：如下图（1）所示，圆锥的侧面展开图是一个扇形，如果圆锥的底面半径为 r，母线 长为l，那么这个扇形的弧长等于圆锥底面周长C=πr，半径等于圆锥侧面的母线长为l，由此可得它的侧面 积是 ． 1 S  Cl rl 圆锥侧 2 ②圆锥的表面积：S圆锥表 r2 rl ． Ⅳ、圆台的表面积 ①圆台的侧面积：如上图（2）所示，圆台的侧面展开图是一个扇环．如果圆台的上、下底面半径分别 为r＇、r，母线长为l，那么这个扇形的面积为 (rr)l ，即圆台的侧面积为S 圆台侧 = (rr)l ． ②圆台的表面积： ． S (r2 r2 rlrl) 圆台表 1．在直三棱柱ABCABC 中，ABBCBB ，ABBC，点P在四边形AABB内（含边界）运动，当 1 1 1 1 1 1 CP 2CC 时，点P的轨迹长度为π，则该三棱柱的表面积为（ ） 1 1 A．4 B．104 2 C．124 2 D．164 2 【答案】C 【详解】 设ABBCBB a，因为ABBC，所以由棱柱的性质可得AB BC ， 1 1 1 1 1 因为BB 平面ABC ，BC 平面ABC ，所以BB BC ， 1 1 1 1 1 1 1 1 1 1 1 1 又因为A 1 B 1 B 1 C 1 ，A 1 B 1 BB 1 B 1 ，A 1 B 1 ,BB 1 平面ABB 1 A 1 ， 所以CB 平面ABBA ， 1 1 1 1 点P在四边形AABB内（含边界）运动，当CP 2CC  2a时， 1 1 1 1 BP 2a2a2 a，这意味着点P是在以B 为圆心a为半径的圆弧上运动， 1 1 1 1 该圆弧弧长是 圆周周长，由题意 2πaπ，解得a2， 4 4 1 1 所以该三棱柱的表面积为22222 22 22 22124 2. 2 2 2．若正四棱锥的高为8，且所有顶点都在半径为5的球面上，则该正四棱锥的侧面积为（ ） - 54 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}A．24 B．32 C．96 D．128 【答案】C 【详解】 如图所示，设P在底面的投影为G，易知正四棱锥PABCD的外接球球心在PG上， 由题意球O的半径PO AO5,OG 853， 2 所以AG 5232 4，PA 8242 4 5，则AB8 4 2， 2  2  2 故 PAB中，边AB的高为 4 5  2 2 6 2，  1 所以该正四棱锥的侧面积为4 4 26 2 96. 2 3．已知正三棱台ABCABC 的上底面积为 3，下底面积为4 3，高为2，则该三棱台的表面积为（ ） 1 1 1 A．5 33 39 B．3 39 C．5 318 D．18 【答案】A 【详解】由面积公式可得正三棱台上下底面边长分别为2和4， 设C 在底面ABC内的射影为H，作HQBC于Q， 1 CH 平面ABC，BC平面ABC，则有CH BC， 1 1 又HQBC，C 1 H  HQH ，C 1 H,HQ平面C 1 HQ，所以BC平面C 1 HQ， CQ平面CHQ，所以BCCQ， 1 1 1 由BC4，BC 2，BB CC ，则CQ1， 1 1 1 1 π 3 39 又HCQ ，所以HQ ，则CQ CH2HQ2  ， 6 3 1 1 3 24 39 故三棱台的侧面积为  33 39，表面积为5 33 39. 2 3 考点 2 棱柱、棱锥、棱台的体积 Ⅰ、柱体的体积公式：V =Sh． 棱柱 Ⅱ、锥体的体积公式： ． 1 V  Sh 棱锥 3 Ⅲ、台体的体积公式 ． 1 V  h(S SSS) 棱台 3 Ⅳ、圆台的体积公式 圆台的体积：如果圆台的上、下底面半径分别是r＇、r，高是h，那么它的体积是 - 55 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}． 1 1 V  h(S SSS) h(r2 rrr2) 圆台 3 3 4．已知圆锥的侧面展开图是半径为3的半圆，则该圆锥的体积为（ ） 2π 9 3π 9 3π 2 2π A． B． C． D． 3 2 8 3 【答案】C 【详解】设圆锥底面圆的半径为r，高为h，母线长为l， 3 3 3 则l3，2πr3π，所以r ，所以h l2r2  ， 2 2 1 1 3 2 3 3 9 3 所以该圆锥的体积为 πr2h π    π. 3 3 2 2 8 5．在斜三棱柱ABCABC 中，A ,B 分别为侧棱AA,BB 上的点，且AA BB ，过A,B ,C 的截面将三 1 1 1 0 0 1 1 1 0 0 0 0 1 棱柱分成上、下两个部分的体积之比可以为（ ） 3 4 1 A．2 B． C． D． 2 3 3 【答案】A 【详解】设三棱柱ABCABC 的体积为V ，因为侧棱AA,BB 上各有一动点A ,B ， 1 1 1 1 1 0 0 满足AA BB ，所以四边形A B BA与四边形A B BA的面积相等， 1 0 0 0 0 0 0 1 1 1 1 故四棱锥C AB BA 的体积等于三棱柱ABCABC 的体积的 ，即 V， 1 0 0 1 1 1 1 1 3 3 2 则几何体ABCABC 的体积等于 V ， 0 0 1 3 故过A,B ,C 的截面将三棱柱分成上，下两个部分的体积之比为2:1或1:2. 0 0 1 1 6．如图，往一个正四棱台密闭容器内倒入38cm3的水，水面高度恰好为棱台高度的 ，且AB6cm， 2 AB 2cm，则这个容器的容积为（ ）cm3 1 1 A．52 B．60 C．68 D．76 【答案】A 【详解】设水体对应的台体的高为hcm，则水体对应台体的上底面是边长为4cm的正方形， 1 76 3 由台体的体积公式可得V    426246  h h38，解得h ， 水 3 3 2 - 56 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}1 故容器的高为3cm，容器的容积为V   226226  352  cm3 3 考点 3 球的表面积和体积 7．已知圆台的上底面半径是1，下底面半径是2，且圆台的体积为7π，则该圆台的外接球的表面积为（ ） A．5π B．13π C．20π D．25π 【答案】C 【详解】设圆台的高为h，其外接球的半径为R， 1 因为圆台的体积为7π，可得 π(121222)h7π，解得h3， 3 若球心在圆台的内部，可得 R212  R222 3，解得R 5， 所以外接球的表面积为S 4πR2 4π( 5)2 20π； 若球心在圆台的外部，可得 R212  R222 3，此时无解， 综上可得，外接球的表面积为20π. 8．在三棱锥PABC中，已知PA平面ABC，PA2AB2BC 4，AC 2 2．若该三棱锥的顶点都在 同一个球面上，则该球的体积为（ ） A．4 6π B．12π C．8 6π D．24π 【答案】C 【详解】因为PA平面ABC，PA4，ABBC2，AC 2 2， 所以AB2BC2  AC2，即ABC90． 把三棱锥PABC补成长方体，长方体的体对角线就是外接球的直径2R． 根据长方体体对角线公式 PA2AB2 BC2  422222  1644 2 6，则R 6， 4 4  3 球的体积V  πR3  π 6 8 6π. 3 3 9．已知一个球形容器的容积为4 3π（容器壁厚度忽略不计），在球形容器内放入一个正三棱柱，则正三 棱柱侧面积的最大值为 ． 【答案】9 3 4 【详解】设球形容器的半径为R，则 πR3 4 3π，得R 3， 3 设正三棱柱的底面边长为a，高为h， a 3 则正三棱柱的底面外接圆的半径r  a， 2sin60 3 当正三棱柱的所有顶点都在球形容器壁上时，正三棱柱的侧面积才可能取到最大值， h 2 h2 1 h2 1 3 1 3 此时R2    r2   a2 2  a2  ah，当且仅当 h a时取等号． 2 4 3 4 3 3 2 3 3 所以 ah3，即ah3 3， 3 所以正三棱柱侧面积的最大值为33 39 3． - 57 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}3.新高考函数压轴题突破---抽象函数 抽象函数问题是考查学生数学抽象素养的有效载体，这几年，新高考数学试卷中每年都出现了抽象函 数问题，题目常涉及到函数的基本性质(奇偶性、周期性、对称性、单调性等)、函数图像、不等式、复合函 数、导函数等基本内容，同时还蕴含着数形结合、函数与方程、化归等数学思想.由于抽象函数仅仅给出函 数某种性质或满足某种关系，学生在解决此类问题时，常常感到束手无策、不知所措.因此，在考前我们有 必要把这种抽象函数概括总结清楚。 一、 近几年抽象函数考情分析 年份 题号 详细知识点 类型 2020-1 8 函数奇偶性的应用； 函数的基本性质相互转化 根据函数的单调性解不等式； 2020-2 8 函数奇偶性的应用； 抽象函数与不等式的综合性问题 根据函数的单调性解不等式； 2021-2 8 函数奇偶性的应用； 常规赋值法与图像法 函数的周期性的定义与求解； 2022-1 12 抽象函数的奇偶性；函数对称性的应用； 常规赋值法与图像法 函数与导函数图像之间的关系； 2023-1 11 函数奇偶性的定义与判断； 抽象函数与导数的综合性问题 函数极值点的辨析； 2024-1 8 求函数值；比较函数值的大小关系 抽象函数与不等式的综合性问题 二、必备知识 1.掌握基本性质与结论 (cid:3028)(cid:2878)(cid:3029) 对称性：理解轴对称（如 𝑓(𝑎+𝑥)=𝑓(𝑏−𝑥) 对称轴为 𝑥 = ）和中心对称（如 𝑓(𝑎+𝑥)+ (cid:2870) (cid:3028)(cid:2878)(cid:3029) (cid:3030) 𝑓(𝑏−𝑥)=𝑐 对称中心为 (cid:4672) , (cid:4673)）的常见形式。 (cid:2870) (cid:2870) 周期性：熟记周期性结论，例如：𝑓(𝑥+𝑎)=𝑓(𝑥+𝑏) → 周期 𝑇 =|𝑎−𝑏|；𝑓(𝑥+𝑎)=−𝑓(𝑥) → 周 (cid:2869) 期 𝑇 =2𝑎；𝑓(𝑥+𝑎)= → 周期 𝑇 =2𝑎。 (cid:3033)((cid:3051)) 奇偶性：奇函数满足 𝑓(−𝑥)=−𝑓(𝑥)，偶函数满足 𝑓(−𝑥)=𝑓(𝑥)，注意复合函数的奇偶性（如 𝑓(cid:3435)𝑔(𝑥)(cid:3439) 的奇偶性需结合 𝑔(𝑥) 分析）。 2. 赋值法与特殊值法 对抽象函数，通过赋值（如 𝑥 =0,1,−1 等）简化问题。例如：若 𝑓(𝑥𝑦)=𝑦(cid:2870)𝑓(𝑥)+𝑥(cid:2870)𝑓(𝑦)，可令 𝑥 = 𝑦 =0 得 𝑓(0)=0；令 𝑦 =1 可能得到递推关系（如 𝑓(𝑥+1)=𝑓(𝑥)−𝑓(𝑥−1)）。 通过特殊值验证选 项，快速排除错误答案（如2022年新高考Ⅰ卷第12题可通过构造 𝑓(𝑥)=sin𝜋𝑥 验证）。 3. 函数模型化 将抽象函数具体化为熟悉的函数模型（如三角函数、多项式函数）辅助分析： (cid:3095)(cid:3051) 若 𝑓(𝑥+𝑦)+𝑓(𝑥−𝑦)=𝑓(𝑥)𝑓(𝑦)，可联想余弦函数 𝑓(𝑥)=2cos ；若涉及导数，可考虑 𝑓(𝑥)=sin𝑥 或 (cid:2871) 𝑓(𝑥)=𝑒(cid:3051) 等。 4.导数与函数性质结合 导函数与原函数的关系：若 𝑓(𝑥) 关于 𝑥 =𝑎 对称，则 𝑓′(𝑥) 关于点 (𝑎,0) 对称；若 𝑓(𝑥) 为偶函数， 𝑓′(𝑥) 为奇函数，反之亦然。 利用导数研究单调性、极值等（如2022年新高考Ⅰ卷第12题需结合导函数的 对称性）。 5. 逻辑推理与归纳 通过递推关系（如 𝑓(𝑥+1)=𝑓(𝑥)−𝑓(𝑥−1)）推导周期性；结合对称性和周期性简化计算（如求 ∑(cid:2870)(cid:2870) 𝑓(𝑘) 时先确定周期后分组求和）。 (cid:3038)(cid:2880)(cid:2869) 6. 避免常见误区 定义域优先：抽象函数的定义域可能隐含限制（如对数函数需真数大于0）；多解验证：抽象函数的性 质可能对应多个具体函数，需验证是否满足所有条件；避免机械刷题：注重理解本质，如对称性和周期性 的推导逻辑，而非死记结论。 - 58 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}三、2025年预测题： 1.已知函数 f x定义域为R，对x,yR，恒有 f xy f xy2f x f y，则下列说法错误的有（ ） A． f 01 B． f 2x1 f 2x1 1 C． f x f 00 D．若 f 1 ，则 f x周期为6 2 【答案】A 【详解】由 f xy f xy2f x f y， 令x0，y0，有 f 0 f 02f 0 f 0，可得 f 00或1，A错； 当 f 00时，令y0，则 f x f x2f x f 00， f x0， 函数 f x既是奇函数又是偶函数， f 2x1 f 2x1， 当 f 01时，令x0，则 f y f y2f 0 f y，则 f y f y， 函数 f x是偶函数， f 2x1 f 2x1，综上，B正确； 令x y，则 f 2x f 02f2x，故 f 2x f 00， 由于xR，令t2x,tR，即 f t f 00，即有 f x f 00，C正确； 1 若 f 1 ，令y1，则 f x1 f x12f x f 1 f x，所以 f x1 f x f x1， 2 则 f x f x1 f x2， f x1  f x1 f x2   f x1f x2， 所以 f xf x3 f x6，则 f x周期为6，D正确. - 59 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}2.已知函数 f(x)满足 f(x) f(2x)，当x[1,2), f(x)lnx，若在区间[1,4)内，函数g(x) f(x)ax(a 0)有 两个不同零点，则实数a的取值范围是（ ）  ln2 ln2 1  ln2 1 ln2 ln2 A．0,  B． ,  C． ,  D． ,   4   4 2e  4 e  4 2  【答案】A f(x) 【详解】由g(x) f(x)ax0a ，函数g(x) f(x)ax(a 0)有两个不同零点，可转化为 x f(x) x x ya,y 有两个交点，当2x4， f(x) f( )ln x 2 2 lnx ,1x2  x f(x)  故h(x)  x x ln  2  ,2x4  x ln2 f(x) 作图如下，由于h(4) ,若ya,y 有两个交点 4 x  ln2 可得a 0,   4  3.记定义在R上的函数 f x与gx的导函数分别为 fx和gx，若 f x3g3x4， fxgx2，且gx2g2x0，则（ ） A． fxfx B．gx的图象关于直线x2对称 2025 C． f x是周期函数，且其中一个周期为8 D．g(i)0 i1 【答案】BC 【解析】由题意，函数 f x与gx的定义域均为R. 由gx2g2x0求导可得gx2g2x0，即gx2 g2x， 所以gx的图象关于直线x2对称，故B正确； 由 f x3g3x4求导可得 fx3g3x0，  fx gx2, f1x g3x，  fx3 f1x0，则 f x3 f 1xc（c为常数）， 令x1，则有 f 2 f 2c0，所以 f x3 f 1x0，即 f x3 f 1x， 所以 f x f x4，即函数 f x的图象关于直线x2对称. 又由 f x3g3x4可得g3x f x34， 则有gx2 f x44,g2x f x44，  gx2g2x0， f x44 f x440，即 f x4 f x48， 所以函数 f x的图象关于点4,4对称. 所以函数 f x是周期函数，周期T 4 42 8.证明如下： - 60 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}由 f x4 f x48可得 f x f x88， 由上述结论可知 f x f x4，所以 f x4 f x88. 则 f x4 f x4 f x4 f x88，即 f x4 f x8， 又由 f x f x4可得 f x4 f x，所以 f x f x8. 所以 f x是周期函数，且其中一个周期为8，故C正确； 对于A，因为 f x f x4， f x f x8， 若 fxfx，则 f x4 f x80，与 f x4 f x88矛盾.故A错误； 对于D，由 f x3g3x4求导可得 fx3g3x0， 则有 fxg6x0，因为 fxgx2，所以gx2g6x0 则gx2g6xt（t是常数），令x2，可得g4g4t0， 所以gx2 g6x，即函数gx的图象关于直线x4对称. 所以，函数gx也是周期函数，周期T 4 42 8.  gx2g2x0，令x0，可得g20， 根据对称性可知，g6 g20,g1g3 g7g50,g4g8 g4g00， 所以g1g2  g7g80. 2025 所以g(i)g1，g1 不确定是否为0，故D错误. i1 4.已知函数 f x满足：x, yR, f xy f xy2f x f y，且 f 10，那么（ ） A． f 01 B． f 12 1 C． f x f x D．若 f π ，则 f x2π f x 2 【答案】AC 【解析】对于A，令x1，y0， f 1 f 12f 1 f 0， 因为 f 10，所以 f 01，故A正确； 设 f xcosx，则 f xy f xycosxycosxycosxcosysinxsinycosxcosysinxsiny 2cosxcosy2f x f y 显然满足条件，但是 f 1cos12，故B错误； 对于C，令x0， f y f y2f 0 f y2f y，所以 f y f y， 又yR，所以 f x为偶函数，即 f x f x，故C正确； x 对于D，设 f xcos ，类似A中推导，可知满足题设条件， 3 但最小正周期是6π，故D错误 - 61 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}4.折展乾坤，向量破题——新高考立体几何及答题全解析 一、考情分析 二、基本知识点 【知识点1 空间几何体表面积与体积的常见求法】 1．求几何体体积的常用方法 (1)公式法：直接代入公式求解. (2)等体积法：四面体的任何一个面都可以作为底面，只需选用底面面积和高都易求出的形式即可. (3)补体法：将几何体补成易求解的几何体，如棱锥补成棱柱，三棱柱补成四棱柱等. (4)分割法：将几何体分割成易求解的几部分，分别求体积. 2．求组合体的表面积与体积的一般方法 求组合体的表面积的问题，首先应弄清它的组成部分，其表面有哪些底面和侧面，各个面的面积应该 怎样求，然后根据公式求出各个面的面积，最后相加或相减.求体积时也要先弄清各组成部分，求出各简单 几何体的体积，再相加或相减. 【知识点2 几何法与向量法求空间角】 1．几何法求异面直线所成的角 (1)求异面直线所成角一般步骤： ①平移：选择适当的点，线段的中点或端点，平移异面直线中的一条或两条成为相交直线； ②证明：证明所作的角是异面直线所成的角； ③寻找：在立体图形中，寻找或作出含有此角的三角形，并解之； ④取舍：因为异面直线所成角 的取值范围是 ，所以所作的角为钝角时，应取它的补角作为异面 直线所成的角. 2．用向量法求异面直线所成角的一般步骤： (1)建立空间直角坐标系； (2)用坐标表示两异面直线的方向向量； - 62 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}(3)利用向量的夹角公式求出向量夹角的余弦值； (4)注意两异面直线所成角的范围是 ，即两异面直线所成角的余弦值等于两向量夹角的余弦值的 绝对值. 3．几何法求线面角 (1)垂线法求线面角(也称直接法)： ①先确定斜线与平面，找到线面的交点B为斜足；找线在面外的一点A，过点A向平面 做垂线，确定 垂足O； ②连结斜足与垂足为斜线AB在面 上的投影；投影BO与斜线AB之间的夹角为线面角； ③把投影BO与斜线AB归到一个三角形中进行求解(可能利用余弦定理或者直角三角形. (2)公式法求线面角(也称等体积法)： 用等体积法，求出斜线PA在面外的一点P到面的距离，利用三角形的正弦公式进行求解. 公式为： ，其中 是斜线与平面所成的角，h是垂线段的长，l是斜线段的长. 4．向量法求直线与平面所成角的主要方法: (1)分别求出斜线和它在平面内的射影直线的方向向量，将题目转化为求两个方向向量的夹角(或其补角)； (2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角或钝角的补角，取其余 角就是斜线和平面所成的角. 5．几何法求二面角 作二面角的平面角的方法： 作二面角的平面角可以用定义法，也可以用垂面法，即在一个半平面内找一点作另一个半平面的垂线， 再过垂足作二面角的棱的垂线，两条垂线确定的平面和二面角的棱垂直，由此可得二面角的平面角. 6．向量法求二面角的解题思路: 用法向量求两平面的夹角：分别求出两个法向量，然后通过两个平面的法向量的夹角得到两平面夹角 的大小. 【知识点3 空间距离的求解策略】 1．向量法求点到直线距离的步骤： (1)根据图形求出直线的单位方向向量 . (2)在直线上任取一点M(可选择特殊便于计算的点).计算点M与直线外的点N的方向向量 . (3)垂线段长度 . 2．求点到平面的距离的常用方法 (1)直接法：过P点作平面 的垂线，垂足为Q，把PQ放在某个三角形中，解三角形求出PQ的长度就 是点P到平面 的距离. ②转化法：若点P所在的直线l平行于平面 ，则转化为直线l上某一个点到平面 的距离来求. ③等体积法. ④向量法：设平面 的一个法向量为 ，A是 内任意点，则点P到 的距离为 . - 63 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}【知识点4 立体几何中的探索性问题的求解策略】 1．与空间向量有关的探索性问题的求解策略： 在立体几何中，与空间向量有关的探究性问题主要有两类：一类是探究线面的位置关系；另一类是探 究线面角、二面角或点线面距离满足特定要求时的存在性问题． 解决这两类探索性问题的解题策略是：先建立空间直角坐标系，引入参数（有些是题中已给出），设 出关键点的坐标，然后探究这样的点是否存在，或参数是否满足要求，从而作出判断． 【知识点5 立体几何中的轨迹问题及其解题策略】 1．立体几何中的轨迹问题 立体几何中的轨迹问题，这是一类立体几何与解析几何的交汇题型，既考查学生的空间想象能力，即 点、线、面的位置关系，又考查用代数方法研究轨迹的基本思想，培养学生的数学运算、直观想象等素养． 2．立体几何中的轨迹问题的求解方法 解决立体几何中的轨迹问题有两种方法： 一是几何法：对于轨迹为几何体的问题，要抓住几何体中的不变量，借助空间几何体（柱、锥、台、 球）的定义；对于轨迹为平面上的问题，要利用降维的思想，熟悉平面图形（直线、圆、圆锥曲线）的定 义． 二是代数法：在图形中，建立恰当的空间直角坐标系，利用空间向量进行求解． 三、向规范答题拿分 高考数学评卷原则：给 1 分有理、扣 1 分有据、宽严适度、始终如一。为深入贯彻这一原则，前期强 化培训、规范操作，认真听取技术组讲解网上评卷操作方法。强调《试题参考答案和评分参考》及《评分 细则》的学习。按照要求，凡不参加评分参考和评分细则学习者不得正式评卷。再次，评卷老师要全部参 与试评。在深入学习《评分细则》的基础上，拿出一整天的时间进行试评，强化评卷老师对评分细则的掌 握情况。在试评过程中要对评分标准进行深入讨论和分析，质检员会集中大家的意见再次修订《评分细则》， 正式评阅前报领导小组备案。这样严谨的评卷流程确保了评分的公正性和一致性。 正式评阅后，要严格按照评分标准评阅，不得自立评分标准，始终如一，宽严适度，防止偏宽、偏严 和错评、漏评。有什么特殊情况必须向小组长题组长报告。对于特殊情况，小组长和题组长会进行及时讨 论，并在必要时与全体评卷老师共同商榷，确保每一位评卷老师对特殊情况的处理都能够达成一致。 数学高考评卷流程分三部分：评卷、仲裁、质检。采用“双评”加“三评”再加“仲裁”，最后是“质检”的五 重保险的评卷模式，确保了评卷的公平、公正、准确。每份答卷至少由两名评卷人员评分（双评），而且 彼此看不到对方的分数，两名评卷人员不是固定组合，电脑随机派送，若两人所给分数误差不超过 2 分， 那就是有效分数。如两人所给分数误差超过 2 分，由第三个人重新评阅（三评），若三评和其中一个误差 不超过 2 分，就不进入仲裁了。若三人两两差距仍超过 2 分，就要进入仲裁，也就是由小组长裁定，最后 给定分数。最后分数与评卷分数差，将记录评卷的两个或三个老师的有效率，如果误差超过 2 分，将记为 无效分。误差的多少及比率将作为考评评卷老师的重要依据。 - 64 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}【2024年新高考2卷第17题】：如图，平面四边形ABCD中，AB8，CD3，AD5 3，ADC90， BAD30，点E，F满足 ， ，将△AEF 沿EF翻折至 PEF，使得 ．  2  1  PC4 3 AE AD AF  AB 5 2 (1)证明：EF PD； (2)求平面PCD与平面PBF所成的二面角的正弦值． 【国标答案】  2  1 （1）由AB8,AD5 3,AE AD,AF  AB，得AE 2 3,AF 4 5 2 又BAD30，在△AEF 中，由余弦定理得 3 EF  AE2AF22AEAFcosBAD  1612242 3 2……………………………………………2 分 2 所以AE2EF2  AF2，则 AE EF ，即EF  AD 所以EF  PE …………………………………4 分 又 PE DE  E, PE、DE平面PDE ，所以 EF 平面PDE ，又 PD平面PDE ，故 EF PD ；……6分  （2）连接CE，由ADC90,ED3 3,CD3，则CE2 ED2CD2 36， 在  PEC中，PC 4 3,PE 2 3,EC 6，得EC2PE2  PC2，所以PEEC 由（1）知PE EF，又 EC EF E,EC、EF 平面ABCD ，  所以PE 平面ABCD，又ED平面ABCD，所以PE ED，…………………………………………8 分 则PE,EF,ED两两垂直，建立如图空间直角坐标系Exyz， 则E(0,0,0),P(0,0,2 3),D(0,3 3,0),C(3,3 3,0),F(2,0,0),A(0,2 3,0)， 由F 是AB 的中点，得B(4,2 3,0)，……………………………………………………………………10 分 - 65 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}    所以PC(3,3 3,2 3),PD(0,3 3,2 3),PB(4,2 3,2 3),PF (2,0,2 3)，   设平面PCD和平面PBF的一个法向量分别为n(x,y ,z ),m(x ,y ,z )， 1 1 1 2 2 2  n  P  C  3x 3 3y 2 3z 0  m  P  B  4x 2 3y 2 3z 0 则 n  P  D  3 1 3y 2 1 3z 0 1 ， m  P  F  2x 2 2 3z 2 0 2 ， 1 1 2 2 令y 2,x  3，得x 0,z 3,y 1,z 1， 1 2 1 1 2 2   所以n(0,2,3),m( 3,1,1) ，………………………………………………………………………13 分 mn 1 65 所以 cos m,n    ，……………………………………………………………14 分 m n 5 13 65 8 65 设平面PCD和平面PBF所成角为，则sin 1cos2 ， 65 8 65 即平面PCD和平面PBF所成角的正弦值为 .………………………………………………………15 分 65 【评分细则】第1问评分细则  2  1 思路一：由AB8,AD5 3,AE AD,AF  AB ，得 AE 2 3,AF 4………………………………1 分 5 2 【评析】见到AE2 3,AF 4中的一个即可得1分 又BAD30，在△AEF 中， 3 由余弦定理得EF  AE2AF22AEAFcosBAD  1612242 3 2……………………………2 分 2 AE 3 【评析】见到EF 2，或  ,即可得1分 AF 2 所以 AE2EF2  AF2，则 AE EF ，即EF  AD ……………………………………………………3 分 【评析】见到 AE2EF2  AF2，EF  AD,EF  AE,EF ED 之一即可得这1分 所以EF  PE ……………………………………………………………………………………………………4 分 又 ，所以 ，……………………………………………5分 PE DE  E, PE、DE平面PDE EF 平面PDE  又 PD平面PDE ，故 EF PD ；…………………………………………………………………………6 分 【评析】只见到 EF 平面PDE ，没有 EF PD 得1分；没见到 EF 平面PDE ，只见到 EF PD 不得分 思路二：1～4分与解法1相同 因为  P  D    P  E    E  D  ，所以         ……………………………5 分 EFPDEF PEED EFPEEFED0 故 EF PD………………………………………………………………………………………………6 分 - 66 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}【评析】见到 E  F    P  E  0，所以EF PD，即可得2分 【评析】若第一问用坐标法来证明，则第二问的7～10分放到第一问来赋分 第2问评分细则 思路一：空间直角坐标系+空间向量 （2）连接CE，由ADC90,ED3 3,CD3，则CE2 ED2CD2 36， 在  PEC中，PC 4 3,PE 2 3,EC 6，得EC2PE2  PC2，所以PEEC………………………7 分 【在新高考的背景下，我要特别强调这一环节的重要性。今后立体几何大题预计仍将包含以下特点：相对 比较容易发现以谁为原点进行建系，但题目条件中并不会直接提供三条直线两两互相垂直。在建系之前， 必须经历一个简要的证明过程】 由（1）知PE EF，又 EC EF E,EC、EF 平面ABCD ，  所以PE 平面ABCD，又ED平面ABCD，所以PE ED，……………………………………………8 分 则PE,EF,ED 两两垂直，建立如图空间直角坐标系Exyz，……………………………………………9 分 【评析】在图上做出直角坐标系即可的1分 则E(0,0,0),P(0,0,2 3),D(0,3 3,0),C(3,3 3,0),F(2,0,0),A(0,2 3,0)， 由F 是AB的中点，得B(4,2 3,0)，……………………………………………………………………………10分 【评析】有一个点的坐标对即可得1分     所以PC (3,3 3,2 3),PD(0,3 3,2 3),PB(4,2 3,2 3),PF (2,0,2 3)，   设平面PCD和平面PBF的一个法向量分别为n(x,y ,z ),m(x ,y ,z )， 1 1 1 2 2 2  n  P  C  3x 3 3y 2 3z 0  m  P  B  4x 2 3y 2 3z 0 则 n  P  D  3 1 3y 2 1 3z 0 1 ， m  P  F  2x 2 2 3z 2 0 2 ， 1 1 2 2 【评析】有列式求法向量即可得1分，用行列式也同样给分   令 y 2,x  3 ，得x 0,z 3,y 1,z 1，所以n(0,2,3),m( 3,1,1)，……………………13 分 1 2 1 1 2 2 【评析】得一个法向量得2分，得两个法向量得3分 mn 1 65 所以cos m,n    ，……………………………………………………………………14 分 m n 5 13 65 - 67 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}【评析】有公式或结果对即可得1分 8 65 设平面PCD和平面PBF所成角为，则sin 1cos2 ， 65 8 65 即平面PCD和平面PBF所成角的正弦值为 .…………………………………………………………15 分 65 mn 【评析】出现cos m,n  等公式错误情况，但结果对的情况下扣1分； m n 其他建系方式： 思路二: 纯几何+二面角定义 延长FB,DC交于点 G ,点 G,P 是平面PCD与平面PBF的公共点,所以面PCD∩面PBF=PG ,过点D做PG 的垂 线交PG于点M ,过点M做FG的垂线交FG于点N ,连接DN ,图中∠DMN即为平面PCD与平面PBF的二面角的平 面角。 因为 EF//GD ,因此 GD⊥ 面 EPD⇒GD⊥PD ……………………………………………………………8 分 在 Rt△PED 中，PD=√PE(cid:2870)+DE(cid:2870) =√39 在 Rt △GPD 中, GD=5,PD=√39 ，PG=√PD(cid:2870)+GD(cid:2870) =8 ………………………………………9 分 根据面积不变性，DM= (cid:2900)(cid:2888)⋅(cid:2891)(cid:2888) = (cid:2873)√(cid:2871)(cid:2877) …………………………………………………………………10 分 (cid:2900)(cid:2891) (cid:2876) (cid:2873) (cid:2870)(cid:2873) 在 Rt△DMG 中，MG=GD⋅cos∠DGM=5× = (cid:2876) (cid:2876) (cid:2874)(cid:2872)(cid:2878)(cid:2871)(cid:2874)(cid:2879)(cid:2869)(cid:2874) (cid:2875) 在 △PFG 中, PF=4,PG=8,GF=6 ,余弦定理，cos∠PGF= = (cid:2870)×(cid:2876)×(cid:2874) (cid:2876) 在 Rt△NMG 中，NG= (cid:3014)(cid:3008) = (cid:2870)(cid:2873) ⇒MN= (cid:2870)(cid:2873)√(cid:2869)(cid:2873) ……………………………………………………11分 (cid:3030)(cid:3042)(cid:3046)∠(cid:3017)(cid:3008)(cid:3007) (cid:2875) (cid:2873)(cid:2874) 在 △DNG 中, ∠DGN=60∘ ,余弦定理，DN(cid:2870) =NG(cid:2870)+GD(cid:2870)−NG⋅GD= (cid:2870)(cid:2873)×(cid:2871)(cid:2877) ……………………12 分 (cid:2872)(cid:2877) 在 △DNM 中,根据余弦定理，cos∠DMN= (cid:2888)(cid:2897)(cid:3118)(cid:2878)(cid:2897)(cid:2898)(cid:3118)(cid:2879)(cid:2888)(cid:2898)(cid:3118) =− √(cid:2874)(cid:2873)…………………………………………14 分 (cid:2870)(cid:2888)(cid:2897)⋅(cid:2897)(cid:2898) (cid:2874)(cid:2873) 平面 PCD 与平面 PBF 所成角二面角的正弦值为sinα=√1−cos(cid:2870)∠DMN= (cid:2876)√(cid:2874)(cid:2873)…………………15 分 (cid:2874)(cid:2873) 思路三：纯几何+三垂线 延长 𝐹𝐵,𝐷𝐶 交于点 𝐺 ,点 𝐺,𝑃 是平面 𝑃𝐶𝐷 与平面 𝑃𝐵𝐹 的公共点,所以面 𝑃𝐶𝐷∩ 面 𝑃𝐵𝐹 = 𝑃𝐺 , - 68 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}通过计算得 𝐶𝐺 =𝐵𝐺 =𝐵𝐶 =2，过点F做面PGD的垂线，垂足为M，过M作MN⊥PG,连接FN 作EQ⊥ PD于 Q，则∠FNM是平面 PCD 与平面 PBF 所成的二面角的平面角。…………………7 分 ∵ EF⊥面PMD∴EF⊥EQ.∵PD⊥EQ,PD∩CD=D,∴EQ⊥面PGD ，EQ为点E到面PGD 的距离 ∵EF//CD∴FM=EQ .…………………………………………………………………………………………9 分 在Rt∆PED中, EQ= (cid:2900)(cid:2889)⋅(cid:2897)(cid:2888) = (cid:2870)√(cid:2871)⋅(cid:2871)√(cid:2871) = (cid:2869)(cid:2876) (cid:2900)(cid:2888) √(cid:2871)(cid:2877) √(cid:2871)(cid:2877) (cid:2869)(cid:2876) ∴FM=EQ = ……………………………………………………………………………………………10 分 √(cid:2871)(cid:2877) (cid:2870) 在Rt∆EDG中,EG(cid:2870) =(cid:3435)3√3(cid:3439) +5(cid:2870) =52 在Rt∆PEG中,PG =(cid:3495)(cid:3435)2√3(cid:3439) (cid:2870) +52=√64=8 在Rt∆PFG中, cos∠PGF= (cid:2874)(cid:3118)(cid:2878)(cid:2876)(cid:3118)(cid:2879)(cid:2877)(cid:3118) = (cid:2875) ，sin∠PGF= √(cid:2869)(cid:2873) (cid:2870)×(cid:2874)×(cid:2876) (cid:2876) (cid:2876) (cid:2869)×(cid:2873) (cid:2871)(cid:2878)(cid:2873) ∵FN⊥PG∴FN=FG⋅sin∠PGF=6× = …………………………………………………………13 分 (cid:2876) (cid:2872) 平面 PCD 与平面 PBF 所成角二面角的正弦值为sin∠FNM= (cid:2890)(cid:2897) = √(cid:2876) × (cid:2872) = (cid:2876)√(cid:2874)(cid:2873) ………………15 分 (cid:2890)(cid:2898) √(cid:2871)(cid:2877) (cid:2871)√(cid:2869)(cid:2873) (cid:2874)(cid:2873) 易错提醒： （1）逻辑关系混乱，分不清哪些是得分点；第一问的证明，学生对由线线垂直，得线面垂直，再得线 线垂直掌握的不好，但本题中若无线面垂直，只有线线垂直则扣两分，课本中的重要定理和性质，平时教 学中需重点强调； （2）在利用向量法求解中，第 7～8 分这两个得分点缺失的同学比较多，也就是建系前的需要证明三 条直线两两互相垂直；同时建系强调右手系虽然其他建系法也正确，但会增加运算量，更容易导致运算错 误； （3）运算能力差，点坐标求错，法向量解错，只得一分，后续也存在不少的运算问题，一般的学生需 要重点加强求点、求法向量的训练。 （4）部分考生在选择的建系方式不恰当，进而导致了运算过程的复杂化，并最终未能获得准确 的结果。 （5）部分考生运用纯几何法，但他们大多未能成功得出最终答案。通过对前述两种纯粹采用几 何方法分析，我们发现，纯几何分析方法在应对此类问题时，对思维的要求相当高，且本题所蕴含的 计算量亦相当庞大，比向量法还大。因此，在考试中，选择纯几何法可能并不构成显著的优势。 - 69 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}四、典例分析 典例1．如图，四棱锥PABCD的所有顶点均在同一个球的球面上，且AB AD4，BCCD，PB平 面PAD． (1)证明：平面PAB平面ABCD； (2)求四棱锥PABCD体积的最大值； (3)当四棱锥PABCD的体积最大时，求直线PC与平面PBD所成角的正弦值． 【详解】（1）由题意知四边形ABCD存在外接圆，故BADBCDπ， π 而BCCD，即BCD ， 2 π 所以BAD ，故ABAD， 2 由PB平面PAD，AD平面PAD，可得PB AD， 而ABPBB，AB平面PAB，PB平面PAB， 故AD平面PAB， 又因为AD平面ABCD，故平面PAB平面ABCD． （2）如图，过点P作PH  AB，垂足为H， 由（1）平面PAB平面ABCD，又平面PAB平面ABCD  AB，PH 平面PAB， 所以PH 平面ABCD． 设四边形ABCD的面积为S， 1 1 则四棱锥PABCD的体积V  PHS  PHS S ， 3 3 ABD BCD 因为AB AD4，ABAD，所以S 8， △ABD - 70 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}因为PB平面PAD，PA平面PAD， 所以PBPA，则点P在以AB为直径的圆上， AB 当PAPB时，PH最大，最大值为 2． 2 因为BCCD，所以点C在以BD为直径的圆上，且BD AB2AD2 4 2， 当BCCD4时，S 最大，最大值为8，此时底面ABCD是正方形． △BCD 1 32 所以四棱锥PABCD体积的最大值为V  216 ． max 3 3 （3）以A为坐标原点，AB，AD所在直线分别为x，y轴，过点A且与平面ABCD垂直的直线为z轴， 建立空间直角坐标系，如图． 由（2）可知B4,0,0，D0,4,0，P2,0,2，C4,4,0．    所以PB2,0,2，BD4,4,0，PC2,4,2． 设平面PBD的法向量为n  x,y,z，   P  B  n2x2z0 则   B  D  n4x4y0 ， 取x1，则y1，z1 所以n  1,1,1为平面PBD的一个法向量， 设直线PC与平面PBD所成的角为， n  P  C  242 2 则sin   ． n  P  C  3 4164 3 2 所以直线PC与平面PBD所成角的正弦值为 . 3 典例2．座落于杨浦滨江的世界技能博物馆由百年历史文化保护建筑改建而成，其中的支柱保留了原有的正 八棱柱，既考虑了结构力学优势，又体现了对历史建筑的尊重和传承.如图，O､O分别为正八棱柱的上下两 1 个底面的中心，已知OA1,AA 4. 1 (1)求证：BCCF； 1 (2)求点O到平面ACG 的距离. 1 【详解】（1） - 71 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}连接CF， 因为底面为正八边形，所以CF BC， 又正八棱柱侧棱CC 底面ABCDEFGH ，BC底面ABCDEFGH ， 1 所以CC 1 BC，CC 1 CF C,CC 1 ,CF 平面CFC 1 ， 所以BC 平面CFC ， 1 又CF 平面CFC ，所以BCCF. 1 1 1 （2） 连接OC,OG ， 1 因为OA1,AA 4， 1 360 由正八边形ABCDEFGH 的性质可得AOB 45，OCOA1，GG 为G 到底面AOC的距离，GG 4， 8 1 1 1 1 1 所以S  11 ， △AOC 2 2 由勾股定理可得，AC2  AO2CO2 2， 又AG2  AC2 2，所以AG  216  183 2， 1 又CG2AO2，所以CG  416  20 2 5， 1 1 因为AC2AG2 CG2，所以AC AG ，即S   23 2 3， 1 1 1 ACG1 2 设点O到平面ACG 的距离为d ， 1 1 1 则V V ，即 S d  S 4，即3d 2， OACG1 G1OAC 3 ACG1 3 AOC 2 2 解得d  ，所以点O到平面ACG 的距离为 . 3 1 3 典例3．如图，四边形ABCD为菱形，EF //平面ABCD，过EF的平面交平面ABCD于AC，EF  AC  EC 2． (1)求证：DE//平面ABF ； - 72 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}(2)若平面ABCD平面ACEF，ACE 60，且四棱锥EABCD的体积是2 3． ①求BD的长； ②求直线ED与平面BCE所成角的正弦值． 【详解】（1）证明：∵EF//平面ABCD，过EF的平面交平面ABCD于AC， ∴EF//AC，又∵EF  AC  EC，∴四边形ACEF为菱形 ∴AF//CE，∵AF 平面ABF ，CE平面ABF ，∴CE//平面ABF . 又∵四边形ABCD为菱形，∴同理CD//平面ABF ， ∵CD  CEC，CE,CD平面CDE，∴平面CDE//平面ABF ， 又DE平面CDE，∴DE//平面ABF ； （2）①连接BD交AC于点O，连接EO， ∵ACEC，且ACE 60，则△ACE为等边三角形， 又四边形ABCD为菱形，则O为AC中点，∴OE AC 又∵平面ABCD平面ACEF，且交线为AC ∴OE 平面ABCD ∵EF  AC  EC 2，∴OE 3 1 1 1 ∴V   BDAC 3 BD2 32 3 EABCD 3 2 6 ∴BD6. ②建系：以O为原点，OB为x轴，OC为y轴，建立直角坐标系， ∴O0,0,0 ，E  0,0, 3  ，B3,0,0，D3,0,0，C0,1,0，          ∴DE 3,0, 3 ，BE 3,0, 3 ，CE  0,1, 3 ， 令平面BCE的法向量为n  x,y,z，则   C   B   E E      n n    0 0 ，       3 y x   3 3 z z   0 0 ，∴n  1,3, 3  设ED与平面BCE所成角为，  D  E  n ∴sin cos  D  E  ,n   39 .  D  E  n 13 典例4．如图，四边形ABCD是圆O所有内接四边形中面积最大的四边形，P为平面ABCD外一点，且 π PAD≌ BAD，PAB ，E是PB的中点.   3 - 73 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}(1)证明PD//平面AEC； (2)求二面角DBPA的余弦值. 【详解】（1）设圆O的半径为rr0， 1 1 所以S S S  ACBD 2r2r2r2， ABCD ABD CBD 2 2 当且仅当ACBD2r时取等号． 所以当ABCD为正方形时，面积最大， 所以AC，BD交于点O，连接OE， 因为O为BD中点，E为PB中点， 所以OE//PD，又OE平面AEC，PD 平面AEC， 所以PD//平面AEC； π π （2）因为PAB ， PAD≌ BAD，所以PA AB，PDBD，PADBAD ，   3 2 所以 PAB为正三角形，  所以AE PB， 又因为ADAB，ADPA，PA  AB A，PA,AB平面PAB， 所以AD平面PAB，又AE平面PAB， 所以AD  AE ． 又因为AD//BC，所以BC AE， 又BC  PBB，BC,PB平面PBC，所以AE 平面PBC， 因为AD平面PAB，PB平面PAB，所以AE PB， 连接DE，又AD PB，AEAD A，AE,AD平面ADE， 所以PB平面ADE，DE平面ADE，所以DEPB， 所以AED为DPBA的平面角， 2  2  2r 6 6 14 又AE 2r    r，AD 2r，所以DE r22r2  r，  2  2 4 2   6 r AE 2 21 21 所以cosAED   ，所以二面角DPBA的余弦值为 . DE 14 7 7 r 2 典例5．在平面四边形ABCD中，AD AC，AC BC ，如图1所示.现将图1中的 ABC沿AC折起，使  点B到达点P的位置，且平面PAC 平面PAD，如图2所示. - 74 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}(1)求证：ADPC； AD (2)若PC  AC ，二面角APDC的大小为60，求 的值. AC 【详解】（1） 作CE AP与E，  平面PAC 平面PAD，平面PAC  平面ACDPA,CE平面PAC， CE 平面PAD,因为AD平面PAD，CEAD, ADAC,ACCEC，AC,CE平面PAC,  AD平面PAC，又因为PC平面PAC，AD PC. （2） BC  AC,PC AC,  又  PCAD，AC  AD A,AC,AD平面ACD,PC 平面ACD, 设PC  AC a，ADx 0 建立如图所示坐标系 则C0,0,0，A0,a,0，Dx ,a,0，P0,0,a， 0     CP0,0,a，CDx ,a,0，AP0,a,a,ADx ,0,0, 0 0  设平面PCD的法向量n x,y,z ， 1 1 1 1    n CP0 az 0   n  1 1 C  D  0 即 x 1 x 1 0 ay 1 0 ，取x 1 a，则y 1 x 0 ，z 1 0，n 1 a,x 0 ,0  设平面PAD的法向量n x ,y ,z ， 2 2 2 2    n AP0 ay az 0   n  2 2   A  D  0 即 x 2 x 0 2 0 2 ，取y 2 1，则x 2 0，z 2 1，n 2 1,0,1,  二面角APDC的大小为60，   cos600  n 1 n 2  x 0  1 ，   n n a2x 2 1212 2 1 2 0 AD 化简得：2x 2 2a2解得：x a即ADa， 1 0 0 AC - 75 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}5.新定义创新问题 一、考情分析 在近五年（2020—2024 年）新高考全国卷中，“新定义题”逐渐成为考查的重点，体现了对学生综合能 力和创新思维的重视。 考点名称 具体内容描述 热度 函数与图像 考查函数的性质、图像变换及其在实际问题中的应用。 ★★★★ 几何与空间 涉及空间几何体的性质、空间关系及其应用问题。 ★★★★ 概率与统计 统计数据分析、概率模型构建及其应用。 ★★★ 数列与极限 数列的性质、极限的计算及其在实际问题中的应用。 ★★★ 建模与应用 通过实际情境构建数学模型，解决现实问题。 ★★★★★ 逻辑推理 逻辑推理能力的考查，包括论证过程的规范表达。 ★★★★ 不等式与优化 不等式的性质及其在优化问题中的应用。 ★★★ 代数与方程 代数方程的解法及其在实际问题中的应用。 ★★★ 数形结合 数学与几何的结合，考查学生的空间想象能力。 ★★★ 探究与发现 强调学生的探究能力和自主学习品质。 ★★★★★ 二、突破策略 创新能力的培养对于考生而言是一个长期且持续的过程，无法在短期内一蹴而就。因此，在日常的训 练中，我们必须有意识地加强对特定题型的练习。为了助力考生更好地应对创新能力解答题，我们特别挑 选了三类题目：新定义型、知识交汇型和创新型。这些题目旨在帮助不同水平的考生进行有针对性的练习， 从而实现在这类解答题上的突破。 三、典例分析 1．空间的弯曲性是几何研究的重要内容，用曲率刻画空间的弯曲性，规定：①多面体顶点的曲率等于2π减 去多面体在该点处所有面角之和；②多面体的总曲率等于多面体所有顶点的曲率之和，多面体各顶点的平 均曲率等于它的总曲率与顶点数之商，其中多面体的面的内角叫作多面体的面角，角度用弧度制．例如： π π 正四面体每个顶点均有3个面角，每个面角均为 ，故其各个顶点的曲率均为2π3 π． 3 3 (1)如图1，已知四棱锥PABCD的底面ABCD为菱形，ADC 60，O为BD的中点，且PO平面ABCD， AB2PO2． ①求该四棱锥在顶点P处的曲率的余弦值； ②求二面角PABD的平面角的正弦值； (2)瑞士数学家莱昂哈德·欧拉是18世纪数学界最杰出的人物之一，他对简单多面体进行研究后，提出了著 名的欧拉定理：简单多面体的顶点数V、棱数E与面数F满足V FE 2．请运用欧拉定理解决下列问题： 碳60（C ）具有超导特性、抗化学腐蚀性、耐高压以及强磁性，是一种应用广泛的材料．它的分子结构十 60 分稳定，形似足球，也叫足球烯，如图2所示．已知碳60（C ）的分子结构是一个由60个C原子构成的 60 分子，这个多面体有60个顶点，试求碳60（C ）各顶点的平均曲率． 60 【详解】（1）①连接AC，由于底面ABCD是菱形，故BD，AC交于点O， 又ADC 60，所以 ABC为正三角形，  - 76 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}1 因AB2PO2，则OA AC 1,OB 2212  3， 2 PO底面ABCD，OA,OB底面ABCD，故POOA，POOB． 且PA PO2OA2  11 2，PB PO2OB2  132， PA2PB2AB2 244 2 由余弦定理得cosAPB   ， 2PAPB 2 22 4 由题意可知四棱锥PABCD的四个侧面三角形全等， 故有APBBPC CPDDPA， 记四棱锥在点P处的曲率为，则2π4APB， 所以coscos2π4APBcos4APB2cos22APB1 2  2cos2APB1 2 12  2 1 1   2 1 1 ．  8  8 ②如图，以点O为原点，直线OA，OB，OP分别为x，y，z轴，建立空间直角坐标系Oxyz， 则O0,0,0，A1,0,0，B  0, 3,0  ，P0,0,1，     所以AP1,0,1，BP 0, 3,1 ． 设平面PAB的一个法向量为n  x,y,z， 则   n n    B    P A   P      3 x y   z z   0 0 ，令y 3，得n  3, 3,3  ，  OP0,0,1为平面ABCD的一个法向量，设二面角PABD的平面角为， O  P  n 30 3031 21 由已知为锐角，则cos   ， O  P  n 211 7 2 7 2 7 所以sin 1cos2 ，即二面角PABD的平面角的正弦值为 ． 7 7 （2）设碳60（C ）共有F个面，给组成多面体的多边形编号，分别为1，2，…，F号， 60 L L L 设第i号（1iF）多边形有L条边，则碳60（C ）共有E  1 2 F 条棱， i 60 2 L L L 由题意，碳60（C ）共有V 2FE2F 1 2 F 60个顶点， 60 2 i号多边形的内角之和为πL 2π， i 所以碳60（C ）的所有多边形的内角之和为πL L L 2πF， 60 1 2 F 所以碳60（C 60 ）的总曲率为2πV   πL 1 L 2 L F 2πF   L L L  2π  2F 1 2 2 F     πL 1 L 2 L F 2πF  4π． 4π π 由已知V 60，所以碳60（C ）各顶点的平均曲率为  ． 60 60 15 - 77 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}2．已知数列b 的前n项和为S ，且b 1，2S nb ，当数列b 的项数大于2时，将数列b 中各项 n n 1 n n1 n n 的所有不同排列填入一个n!行n列的表格中（每个格中一个数字），使每一行均为这n个数的一个排列，将 第i1in!,iN行的数字构成的数列记作a ，将数列a 中的第 j1 jn, jN项记作a ．若对 in in ij i,j，均有a b ，则称数列a 为数列b 的“异位数列”，记表格中“异位数列”的个数为M ． ij j in n (1)求数列b 的通项公式b ； n n (2)当数列b 的项数为4时，求M 的值； n n (3)若数列a 为数列b 的“异位数列”，试讨论a b 的最小值． in n ij j j1 【详解】（1）由题b 1，2b b ，解得b 2， 1 1 2 2 b n2 由2S nb 得2S n1b ，两式作差得2b n1b nb ，即 n2  ， n n1 n1 n2 n1 n2 n1 b n1 n1 b 3 b 4 b 5 b n 所以 3  ， 4  ， 5  ，……， n  n3 ， b 2 b 3 b 4 b n1 2 3 4 n1 b n 累乘得： n  ，即b nn3， b 2 n 2 因为b 1，b 2符合上式，所以b n． 1 2 n （2）由（1）知，b n，所以b  j1 jn, jN， n j 当数列b 的项数为4时，可知b 1，b 2，b 3，b 4， n 1 2 3 4 若数列a 为数列b 的“异位数列”，则：当a 2时，a 1，a 4，a 3；或a 3，a 4，a 1； n n i1 i2 i3 i4 i2 i3 i4 或a 4，a 1，a 2共3种情况． i2 i3 i4 同理当a 3或a 4时，对应的排列各有3种情况，所以M 9． i1 i1 （3）因为数列a 为数列b 的“异位数列”， in n n 所以a b 1in!,1 jn,i, jN，即a  j，所以 a b  a  j 1，所以a b n， ij j ij ij j ij ij j j1 n 当n2k，kN*时，若对任意的 j，都有 a  j 1，a b n取等号， ij ij j j1 此时a 2，a 1，…，a n，a n1， i1 i2 in1 in n 所以当n2k，kN*时，a b 的最小值为n， ij j j1 n 当n2k1，kN*时，a b n的不可能取到等号，因为存在 j，使得 a  j 2， ij j ij j1 将1，2，3，，n分为k组， 不妨为1,2，3,4，……，2k3,2k2，2k1,2k,2k1时， n a b n1可以取到等号， ij j j1 此时a 2，a 1，……，a 2k2，a 2k1，a 2k，a 2k1，a 2k1， i1 i2 i2k3 i2k2 i2k1 i2k i2k1 n 此时a b 2k11122k2n1， ij j j1 n 所以当n2k1，kN*时，a b 的最小值为n1， ij j j1 n 综上，当n为偶数时，a b 的最小值为n； ij j j1 - 78 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}n 当n为奇数时，a b 的最小值为n1． ij j j1 3．在平面直角坐标系xOy中，把一个图形绕定点G旋转一个定角的图形变换叫作旋转变换.定点G叫作旋 转中心，定角叫作旋转角（规定逆时针方向为正）.如果图形上的点Px,y经过旋转变为点Px,y，那 π 么这两个点叫作这个旋转变换的对应点.现将曲线xymm0绕G顺时针旋转 后，得到新曲线E，其变 4 x xcosysin,   换关系为 ，点 2,1 在曲线E上. y xsin ycos (1)求曲线E的方程并确定点G的位置； (2)点P 1 的坐标为1,0，按照如下方式依次构造点P n n2,3,  ：过点P n1 作斜率为2的直线交E于另一点Q n1 ， 设P是点Q 关于x轴的对称点.记P的坐标为x ,y . n n1 n n n （i）求数列x y 的前n项和S ； n n n （ii）记M 为直线PP 与直线Q P 的交点，N 为直线PQ 与直线Q P 的交点，R为直线MN与直线 1 n2 n n1 1 n n1 n2 P Q 的交点，证明：R在定直线上. n1 n1  2 2   x 2 x 2 y,   2xxy, 【详解】（1）依题意，得 即  2 2  2yx y. y x y,   2 2 xyxy2xy2m，故曲线E方程为x2y2 2m.   1  点 2,1 在曲线E上，m ，故曲线E方程为x2y2 1. 2 由对称性可知，点G为坐标原点O. x2y2 1 （2）（i）依题意，得 n n ， x2 y2 1 n1 n1 得x x x x y y y y ①， n n1 n n1 n n1 n n1 又  直线P n Q n 的斜率为2且P n x n ,y n ,Q n x n1 ,y n1 ， y y 2x x ②. n n1 n n1 将②代入①中，得x x 2y y ③， n n1 n n1 将②和③相加，得3x y x y ， n1 n1 n n x y 1 1 从而 n1 n1  ,x y  是首项为1，公比为 的等比数列， x y 3 n n 3 n n  1 n 11    3  3 1 . S   1  n 1 2 3n  1 3 （ii）点R在定直线x1上. 证明如下：  P n1 x n1 ,y n1 ,Q n1 x n2 ,y n2 ， y y 直线P Q 的方程为yy  n2 n1xx  ， n1 n1 n1 x x n1 n2 n1 x y x y y y 令x1，得y n2 n1 n1 n2 n1 n2 . x x n2 n1 y  直线P 1 P n2 的方程为y x n  2 1 x1，直线Q n P n1 的方程为xx n1 ， n2 - 79 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#} xx ,   n1  y x 1 联立 解得Mx , n2 n1 . y n1 x 1 y n2 x1,  n2    x 1 n2 y  直线P 1 Q n 的方程为y x n  1 1 x1 ，直线Q n1 P n2 的方程为xx n2 ， n1  xx ,   n2  y 1x  联立 解得Nx , n1 n2 . y n2 x 1 y n1 x1,  n1    x 1 n1 y 1x  y x 1 n1 n2  n2 n1 直线MN的方程为 y x 1 x 1 x 1 ， y n2 n1  n1 n2 xx  x 1 x x n1 n2 n2 n1 x y x y y y 令x1，得y n2 n1 n1 n2 n1 n2 ， x x n2 n1  x y x y y y  直线P Q 与直线MN的交点坐标为1, n2 n1 n1 n2 n1 n2 ， n1 n1  x x  n2 n1 故点R在定直线x1上. 4．阅读材料一：“装错信封问题”是由数学家约翰伯努利（Johann Bernoulli，1667~1748）的儿子丹尼尔伯努 利提出来的，大意如下：一个人写了n封不同的信及相应的n个不同的信封.他把这n封信都装错了信封，问 都装错信封的这一情况有多少种？后来瑞士数学家欧拉（Leonhard Euler，1707~1783）给出了解答：记都装 错n封信的情况为D 种，可以用全排列n!减去有装正确的情况种数，结合容斥原理可得公式： n D n n!    1 1 1 !  2 1 !   1n n 1 !    ，其中n!12  n  nN* . 阅读材料二：英国数学家泰勒发现的泰勒公式有如下特殊形式：当 f x在x0处n阶可导，则有： f0 fn0 f x f 0 f0x x2  xn  ，注 fnxn3表示 f x的n阶导数，该公式也称   2! n! 麦克劳林公式.阅读以上材料后请完成以下问题： (1)求出D 、D 、D 的值； 2 3 4 (2)写出ex的泰勒展开式（至少有5项）； (3)设 fx ex ex ，gx exex ，x0,，证明： f x  gx. 2 2 x  1 1   1 1 1  【详解】（1）由题意可得D 2!1  1，D 3!1   312， 2  1! 2! 3  1! 2! 3!  1 1 1 1  D 4!1    12419. 4  1! 2! 3! 4! - 80 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}（2）设pxex，则pxex，p2xex，p3xex，， 以此类推可知，对任意的nN，pnxex，则pn01， p20 p30 p40 p50 所以，pxex  p0 p0x x2 x3 x4 x5  2! 3! 4! 5! x2 x3 x4 x5 1x     .  2 6 24 120 f x exex （3）对任意的x0,，要证明  gx，即证 ex ex， x x exex ex ex ex e2x 1 即证x   ， ex ex ex ex+ex e2x1 e2x 1 令hxx ，其中x0， e2x1 4e2x e4x2e2x 1  e2x 1 2 则hx1   0，  e2x1 2  e2x1 2  e2x1 2 所以，函数hx在0,上单调递增， e2x1 故当x0,时，hxh00，即x ，故原不等式得证. e2x1 6.高考前的终极拷问：2025 年考生必看！ 序号 一、函数与导数 ✓或✕ 1 奇函数都过原点，对吗？ 2 函数y= (cid:2869) 在定义域上是减函数，对吗？ (cid:2934) 设函数f(x)的定义域为R，则“∃x>0，使得f(−x)=f(x)”是“f(x)为偶函数”的充要条件， 3 对吗？ 4 函数y=x+ (cid:2869) 的最小值为2，对吗？ (cid:2934) 5 若一个函数存在极大值和极小值，则极大值一定大于极小值，对吗？ 6 函数f(x)=lnx的零点是(1,0)，对吗？ 7 方程 2(cid:2934) =log (cid:3117) x 只有一个解，对吗？ (cid:3118) 8 直线y=2和函数y=|2(cid:2934)−1|有2个交点，对吗？ 9 将函数y=2(cid:2879)(cid:2934)的图像向左平移2个单位后是y=2(cid:2879)(cid:2934)(cid:2878)(cid:2870)，对吗？ - 81 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}10 将函数y=log x的图像向下平移2个单位后的图像与y=log (cid:4672) (cid:2934) (cid:4673)的图像重合，对吗？ (cid:2870) (cid:2870) (cid:2872) 11 将点P(s,t)向右平移1个单位后的坐标为P(cid:4593)(s−1,t)，对吗？ 12 对于m∈R，直线y=x+m和函数f(x)= (cid:2869) −lnx−2x永远不会相切，对吗？ (cid:2934) 13 若 01，则对数 log b<0 ，对吗？ (cid:2911) 14 对于正实数a,b，且 a≠1, b≠1，恒有 log b⋅log a=1 ，对吗？ (cid:2911) (cid:2912) 15 对于定义域内任意x，恒有f(x)=f(2−x)，则函数关于 x=1对称，对吗？ 16 对于定义域内任意x，恒有f(x)+f(2−x)=4，则函数关于(1,2)对称，对吗？ 17 已知函数f(x)= (cid:2869) x(cid:2870)−2x+lnx，则x=1是函数的唯一极值点，对吗？ (cid:2870) 函数f(x)=x(cid:2870)−ax−2的零点一个比 1 大，一个比 1 小，则a的范围是(−1,+∞)，对 18 吗？ 19 若x 是函数f(x)=xe(cid:2934)−1的零点，则x 也是函数f(x)=x+lnx的零点，对吗？ (cid:2868) (cid:2868) 20 若a|a|>b|b|，则a>b，对吗？ 2(cid:2934),x≤1 2(cid:2934),x<1 21 函数f(x)=(cid:3420) 与函数g(x)=(cid:3420) 的值域一样，对吗？ −x+1,x>1 −x+1,x≥1 已知对勾函数f(x)=x+ (cid:2869) ，直线y=m(m∈R)和f(x)相交于A,B两点，则x ⋅x 为定值， 22 (cid:2934) (cid:2885) (cid:2886) 对吗？ 23 函数f(x)=e(cid:2934)⋅lnx是定义域上的单增函数，对吗？ 24 增函数+增函数=增函数，增函数×增函数=增函数，对吗？ 过坐标原点作函数f(x)=e(cid:2934)+x的切线，则切线的斜率为e+1，对吗？ 25 26 对于m∈R，直线y=x+m和函数f(x)= (cid:2869) −lnx−2x永远不会相切，对吗？ (cid:2934) 设f(x)=ax(cid:2870)−2x+1，若对∀x ,x ∈(−1,+∞)，且x ≠x ，都有 (cid:2916)((cid:2934)(cid:3117) )(cid:2879)(cid:2916)((cid:2934)(cid:3118) ) <0成立， 27 (cid:2869) (cid:2870) (cid:2869) (cid:2870) (cid:2934)(cid:3117)(cid:2879)(cid:2934)(cid:3118) 则a的取值范围为a≥−1，对吗？ - 82 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}设函数f(x)满足：若对∀x ,x ∈R，且x ≠x ，都有 (cid:2916)((cid:2934)(cid:3117) )(cid:2879)(cid:2916)((cid:2934)(cid:3118) ) >a，则y=f(x)−ax是 28 (cid:2869) (cid:2870) (cid:2869) (cid:2870) (cid:2934)(cid:3117)(cid:2879)(cid:2934)(cid:3118) 增函数，对吗？ 29 设 a=2 (cid:3117) (cid:3118),b=5 (cid:3117) (cid:3121) ，则a>b，对吗？ 30 设 a= (cid:2922)(cid:2924)(cid:2870) , b= (cid:2922)(cid:2924)(cid:2873) ，则a>b，对吗？ (cid:2870) (cid:2873) 31 设a=sin1,b=sin2,c=sin3，则b>a>c，对吗？ 32 设f(x)是定义在R上的偶函数，若f(x )=f(x )且x ≠x ，则x +x =0，对吗？ (cid:2869) (cid:2870) (cid:2869) (cid:2870) (cid:2869) (cid:2870) 设函数f(x)=ax(cid:2871)+bx(cid:2870)+cx+d(a≠0)，则存在实数a,b,c,d，使得函数f(x)存在唯一 33 极值点，对吗？ 34 已知函数f(x)=2(cid:2934)−2(cid:2879)(cid:2934)−2，则不等式f(x)> (cid:2875) 的解集为(2,+∞)，对吗？ (cid:2872) 35 若a>b>c，则a+b>c，对吗？ 36 不等式 (cid:2869) >1的解集为(−∞,1)，对吗？ (cid:2934) 序号 二、向量 ✓或✕ 37 零向量和任意向量都平行，对吗？ 38 若向量a(cid:4652)⃗//b(cid:4652)⃗,b(cid:4652)⃗//c⃗，则a(cid:4652)⃗//c⃗，对吗？ 39 对于两个不共线的向量a(cid:4652)⃗,b(cid:4652)⃗，若a(cid:4652)⃗+2b(cid:4652)⃗=xa(cid:4652)⃗+yb(cid:4652)⃗，则x=1,y=2，对吗？ 40 对于两个非零向量a(cid:4652)⃗,b(cid:4652)⃗，若a(cid:4652)⃗(cid:2870) =a(cid:4652)⃗⋅b(cid:4652)⃗，则a(cid:4652)⃗=b(cid:4652)⃗，对吗？ 41 对于两个向量a(cid:4652)⃗,b(cid:4652)⃗,(cid:3435)a(cid:4652)⃗⋅b(cid:4652)⃗(cid:3439) (cid:2870) 和a(cid:4652)⃗(cid:2870)⋅b(cid:4652)⃗(cid:2870)的运算结果是一样的，对吗？ 42 将(cid:3627)a(cid:4652)⃗+b(cid:4652)⃗(cid:3627)平方后展开得到(cid:3627)a(cid:4652)⃗+b(cid:4652)⃗(cid:3627) (cid:2870) =a(cid:4652)⃗(cid:2870)+b(cid:4652)⃗(cid:2870)+2a(cid:4652)⃗⋅b(cid:4652)⃗，对吗？ 43 向量a(cid:4652)⃗=(x ,y )和向量b(cid:4652)⃗=(x ,y )共线，则有 (cid:2934)(cid:3117) = (cid:2935)(cid:3117)成立，对吗？ (cid:2869) (cid:2869) (cid:2870) (cid:2870) (cid:2934)(cid:3118) (cid:2935)(cid:3118) 44 向量的平方等于其模长的平方，复数也满足，即a(cid:4652)⃗(cid:2870) =|a(cid:4652)⃗|(cid:2870),z(cid:2870) =|z|(cid:2870)，对吗？ 若a(cid:4652)⃗=(1,−2),b(cid:4652)⃗=(x,4)，若平面内任意向量c⃗，都存在实数λ,μ，使得c⃗ =λa(cid:4652)⃗+μb(cid:4652)⃗成立， 45 则x≠−2，对吗？ - 83 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}46 45.已知|a(cid:4652)⃗|=2(cid:3627)b(cid:4652)⃗(cid:3627)=2,(cid:3451)a(cid:4652)⃗,b(cid:4652)⃗(cid:3455)=60∘，则(cid:3627)a(cid:4652)⃗+b(cid:4652)⃗(cid:3627)=7，对吗？ 在ΔABC中，点P在BC的延长线上，设A(cid:4652)(cid:4652)(cid:4652)(cid:4652)P(cid:4652)⃗=xA(cid:4652)(cid:4652)(cid:4652)(cid:4652)B(cid:4652)⃗+yA(cid:4652)(cid:4652)(cid:4652)(cid:4652)(cid:4652)C⃗，则x+y=1，且x<0,y>0, 47 对吗？ 已知空间中四点坐标分别为A(1,0,1),B(1,1,0),C(0,1,1),D(cid:4672) (cid:2870) , (cid:2870) ,a(cid:4673)，则a= (cid:2870) 时，点D在 48 (cid:2871) (cid:2871) (cid:2871) 平面ABC内，对吗？ 49 设a(cid:4652)⃗=(−1,2),b(cid:4652)⃗=(2,x)，若为(cid:3451)a(cid:4652)⃗,b(cid:4652)⃗(cid:3455)钝角，则x的取值范围是(−∞,1)，对吗？ 设平面α的法向量为m(cid:4652)(cid:4652)(cid:4652)⃗, A是平面α内任意一点，P是平面α外一点，则点P到平面α的距 50 离公式为d= (cid:2885)(cid:4652)(cid:4652)(cid:4652)(cid:4652)(cid:2900)(cid:4652)⃗⋅(cid:4652)(cid:2923)(cid:4652)(cid:4652)⃗，对吗？ |(cid:2923)(cid:4652)(cid:4652)(cid:4652)⃗| 51 已知ΔABC是一个边长为2的等边三角形，则A(cid:4652)(cid:4652)(cid:4652)(cid:4652)B(cid:4652)⃗⋅B(cid:4652)(cid:4652)(cid:4652)(cid:4652)C(cid:4652)⃗=2，对吗？ 设O为等边三角形ΔABC的中心，D为BC的中点，则O(cid:4652)(cid:4652)(cid:4652)(cid:4652)A(cid:4652)⃗+O(cid:4652)(cid:4652)(cid:4652)(cid:4652)B(cid:4652)⃗+O(cid:4652)(cid:4652)(cid:4652)(cid:4652)(cid:4652)C⃗=0(cid:4652)⃗，且 52 A(cid:4652)(cid:4652)(cid:4652)(cid:4652)O(cid:4652)⃗=2O(cid:4652)(cid:4652)(cid:4652)(cid:4652)D(cid:4652)⃗，对吗？ 序号 三、三角函数与解三角 ✓或✕ 53 若tan(α+β)=tanα+tanβ，则tanα⋅tanβ=0，对吗？ 54 已知sinx=tanx，则cosx=1一定成立，对吗？ 55 函数y=tanx的一个对称中心是(cid:4672) (cid:2976) ,0(cid:4673)，对吗？ (cid:2870) 56 函数f(x)=sin(cid:4672)ωx+ (cid:2976) (cid:4673)的两条对称轴之间的距离最小值为 (cid:2976) ，则ω=2，对吗？ (cid:2872) (cid:2870) 57 设函数f(x)=sin(cid:2872)x+cos(cid:2870)x，则函数关于x= (cid:2976) 对称，对吗？ (cid:2872) 58 已知f(x)=√3sin(2x+φ)(0<φ<π)的图像如下，则φ= (cid:2976) 或 (cid:2873)(cid:2976) ，对吗？ (cid:2874) (cid:2874) 59 ∃x∈R，使得sinx+cosx=2，对吗？ 60 函数f(x)=sinx+cosx+2sinxcosx，则函数的最大值为√2+1，对吗？ 61 将函数f(x)=tan(cid:4672)2x+ (cid:2976) (cid:4673)的最小正周期为π，对吗？ (cid:2871) 62 设函数f(x)=sin2ωx+cos2ωx(ω>0)的最小正周期为π，则ω=2，对吗？ - 84 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}63 函数f(x)=cos(cid:2872)x−sin(cid:2872)x的最正周期为π，对吗？ 64 函数f(x)=cos(cid:2872)x+sin(cid:2872)x的最正周期为 (cid:2976) ，对吗？ (cid:2870) 65 函数y=sin(cid:4672)2x− (cid:2976) (cid:4673)和函数y=cos(cid:4672)2x− (cid:2873)(cid:2976) (cid:4673)的图像是重合的，对吗？ (cid:2871) (cid:2874) 点(cid:4672) (cid:2976) ,0(cid:4673)是函数y=2sin(cid:4672)2x− (cid:2976) (cid:4673)和函数y=2cos(cid:4672)2x+ (cid:2976) (cid:4673)−1的共同的对称中心，对 66 (cid:2874) (cid:2871) (cid:2874) 吗？ 67 函数f(x)=|sinx+cosx|和函数g(x)=2cos(cid:2870)x−2的最小正周期都是π，对吗？ 将函数f(x)=sin(cid:4672)2x+ (cid:2976) (cid:4673)向左平移m(m>0)个单位后图形与f(x)重合，则m的最小值 68 (cid:2871) 为π，对吗？ 已知函数f(x)=sin(cid:4672)ωx+ (cid:2976) (cid:4673)(ω>0)，若对于任意实数x，都有f(x)≤f(cid:4672) (cid:2976) (cid:4673)成立，则ω 69 (cid:2874) (cid:2871) 的最小值为1，对吗？ 70 存在ΔABC，使得A=2B和a=2b同时成立，对吗？ 71 在ΔABC中，A>B是sinA>sinB成立的充要条件，对吗？ 72 在ΔABC中，A>B是cosA0，则ΔABC为锐角三角形，对吗？ 78 一个腰长为1的等腰三角形，面积最大值为 (cid:2869) ，对吗？ (cid:2870) 79 若△ABC的面积满足S= (cid:2869) ac，则B= (cid:2976) ，对吗？ (cid:2872) (cid:2874) 80 已知ΔABC中，a=3, b=7,c=8，则ΔABC为钝角三角形，对吗？ 81 已知ΔABC中，a=3, b=7,c=8，则A< (cid:2976) ，对吗？ (cid:2874) - 85 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}序号 四、数列 ✓或✕ 82 存在等差数列的前n项和S 也是等差数列，对吗？ (cid:2924) 83 对于任意一个等差数列，都有a +a =a 成立，对吗？ (cid:2869) (cid:2876) (cid:2877) 84 若数列{a }的前n项和S =2n²+3n+1，则该数列是等差数列。 n (cid:2924) 85 对于任意m,n∈N∗，都有a =a +a ，则是等差数列，对吗？ (cid:2923)(cid:2878)(cid:2924) (cid:2924) (cid:2923) 86 若a 是等差数列，则a ,a ,a ,⋯,a ,a 也是等差数列，且共有n+1项，对吗？ (cid:2924) (cid:2870) (cid:2873) (cid:2876) (cid:2871)(cid:2924)(cid:2879)(cid:2869) (cid:2871)(cid:2924)(cid:2878)(cid:2870) 87 存在等比数列的前n项和S 是等差数列，对吗？ (cid:2924) 88 对于一个数列，每一项都是前一项的2倍，则数列为等比数列，对吗？ 89 对于等比数列{a }满足：a =2a ，则公比q是2吗？ (cid:2924) (cid:2924) (cid:2924)(cid:2878)(cid:2869) 90 等比数列中任意一项都不为0，且公比也不为0，对吗？ 91 等比数列如果是单调数列，则该等比数列的公比q>0且q≠1，对吗？ 92 等比数列的前5项分别为1,a ,a ,a ,a ,16，则a =±4，对吗？ (cid:2869) (cid:2870) (cid:2871) (cid:2872) (cid:2871) 93 对于任意m,n∈N∗，都有a =a ⋅a ，则是等比数列，对吗？ (cid:2923)(cid:2878)(cid:2924) (cid:2924) (cid:2923) 94 设数列{a }与数列{b }均为等比数列，则{a ⋅b }也是等比数列，对吗？ (cid:2924) (cid:2924) (cid:2924) (cid:2924) 95 已知数列a =n(cid:2870)−11n+2，则当n= (cid:2869)(cid:2869) 时，a 取得最小值，对吗？ (cid:2924) (cid:2870) (cid:2924) 96 若a,b,c 成等比，且ac = 4，则b = 2，对吗？ 序号 五、立体几何 ✓或✕ 96 正四面体一定是正三棱锥，对吗？ 97 异面直线是既不平行也不相交的直线，对吗？ 98 直线l//直线m，且m⊂平面α，则l//平面α，对吗？ 99 如果一条直线的方向向量和一个平面的法向量垂直，则该直线平行于平面，对吗？ 100 若平面α⊥平面β，直线l⊥平面α，则l//平面β，对吗？ - 86 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}101 若平面α⊥平面β,α∩β=m，直线l⊥m，且l⊂α，则l⊥平面β，对吗？ 102 一个三棱锥可以每一个面都是直角三角形，对吗？ 103 圆锥的侧面展开图是半圆时，其母线与底面夹角为60°，对吗？ 104 正方体的外接球体积与内切球体积之比为 3√3，对吗？ 105 棱台体积公式仅适用于正棱台，对吗？ 106 二面角的夹角与其法向量夹角的余弦值相等，对吗？ 序号 六、直线与圆的方程 ✓或✕ 107 直线 y=k(x−1)+1是表示所有过点(1,1)的直线，对吗？ 108 和X轴平行的直线的倾斜角一定是0∘，对吗？ 109 两条直线平行，则斜率相等，对吗？ 110 两条直线垂直，则斜率之积为−1,对吗？ 111 原点(0,0)到直线y=k(x−2)的距离最大值为2，对吗？ 112 点P(cosθ,sinθ)到直线x+√3y+4=0距离的最大值为3，对吗？ 113 一条直线的斜率为-1，则其倾斜角为 (cid:2871)(cid:2976) 或− (cid:2976) ，对吗？ (cid:2872) (cid:2872) 过圆内一点作圆的弦长，最长的弦为直径，最短弦和直径垂直，且该点为弦中点，对 114 吗？ “k=−3”是“直线kx−(k+2)y+2=0和直线x−ky−1=0垂直”的充要条件，对 115 吗？ 设点P是圆(x−2)(cid:2870)+(y+1)(cid:2870) =4上的一个动点，则点P的坐标可以写成： 116 (2+2cosθ,−1+2sinθ)，对吗？ 117 过点(2,4)作圆x(cid:2870)+y(cid:2870) =4的切线，则切线方程为3x−4y+10=0，对吗？ 设点P(x ,y )在圆(x−a)(cid:2870)+(y−b)(cid:2870) =r(cid:2870)上，则过点P作圆的切线只有一条，且切线 118 (cid:2868) (cid:2868) 方程为(x −a)(x−a)+(y −b)(y−b)=r(cid:2870)，对吗？ (cid:2868) (cid:2868) - 87 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}在平面直角坐标系中，恰好存在三条不同的直线同时与圆x(cid:2870)+y(cid:2870) =m(m>0)和圆 119 (x−3)(cid:2870)+(y−4)(cid:2870) =1相切，则m=4，对吗？ 序号 七、圆锥曲线 ✓或✕ 120 平面内到两个定点的距离之和为定值的轨迹为椭圆，对吗？ 121 平面内到两个定点的距离之差的绝对值为定值的轨迹为双曲线，对吗？ 122 椭圆(cid:2934)(cid:3118) + (cid:2935)(cid:3118) =1(a>b>0)上的点到焦点F的距离最小值为a−c，对吗？ (cid:2911)(cid:3118) (cid:2912)(cid:3118) 123 对于椭圆(cid:2934)(cid:3118) + (cid:2935)(cid:3118) =1(a>b>0)，若a>2b，则离心率的范围是e> √(cid:2871)，对吗？ (cid:2911)(cid:3118) (cid:2912)(cid:3118) (cid:2870) 过椭圆(cid:2934)(cid:3118) + (cid:2935)(cid:3118) =1右焦点的直线与椭圆交于A,B两点，设A(x ,y ),B(x ,y ),O为坐标原 (cid:2869) (cid:2869) (cid:2870) (cid:2870) 124 (cid:2872) (cid:2871) 点，则ΔAOB的面积可以表示为 |(cid:2935)(cid:3117)(cid:2878)(cid:2935)(cid:3118) | ，对吗？ (cid:2870) 斜率存在的直线与椭圆交于A,B两点，则AB的长度可以用AB=√1+k(cid:2870)|x −x |计算， 125 (cid:2885) (cid:2886) 且该公式在抛物线、圆、双曲线中均可以使用，对吗？ 126 若一条直线和双曲线无公共点，则该直线一定和渐近线平行或重合，对吗？ 127 双曲线x(cid:2870)− (cid:2935)(cid:3118) =λ(λ≠0)的离心率的大小与λ的取值有关，对吗？ (cid:2871) 128 双曲线(cid:2935)(cid:3118) − (cid:2934)(cid:3118) =1的渐近线方程为y=√3x，则离心率为2，对吗？ (cid:2911)(cid:3118) (cid:2912)(cid:3118) 129 设F , F 是双曲线(cid:2934)(cid:3118) −y(cid:2870) =1的左右焦点，点P(cid:3435)−4,√3(cid:3439)，则|PF |−|PF |=4，对吗？ (cid:2869) (cid:2870) (cid:2869) (cid:2870) (cid:2872) 双曲线(cid:2934)(cid:3118) − (cid:2935)(cid:3118) =1(a>0,b>0)的焦点到渐近线的距离等于b，双曲线(cid:2935)(cid:3118) − (cid:2934)(cid:3118) = 130 (cid:2911)(cid:3118) (cid:2912)(cid:3118) (cid:2911)(cid:3118) (cid:2912)(cid:3118) 1(a>0,b>0)的焦点到渐近线的距离也等于b，对吗？ 131 抛物线 y(cid:2870) =4x 上点 P 到焦点距离等于到准线距离，对吗？ 132 抛物线y= (cid:2869) x(cid:2870)的开口向上，焦点坐标为(0,1)，对吗？ (cid:2872) 133 抛物线 y(cid:2870) =4x 的焦点弦长度为 (cid:2872) （θ 为倾斜角），对吗？ (cid:2929)(cid:2919)(cid:2924)(cid:3118)(cid:2968) 序号 八、概率与统计 ✓或✕ 现有3本完全相同的数学书和5本不一样的小说书籍，从这8本书中抽出3本，则抽 134 到的是1本数学2本小说抽法有30种，对吗？ - 88 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}135 设正整数n满足：C(cid:2870) =C(cid:2874)，则n=8，对吗？ (cid:2924) (cid:2924) 136 某人做三道不同的选择题，每一道做对的概率为 (cid:2869) ，则恰好做对一道的概率为 (cid:2872) ，对吗？ (cid:2871) (cid:2870)(cid:2875) 一组数据x ,x ⋯,x 的平均数为x‾，方差为s(cid:2870)，则2x +1,2x +1,⋯,2x +1的平均数 137 (cid:2869) (cid:2870) (cid:2924) (cid:2869) (cid:2870) (cid:2924) 为2x‾+1，方差为4s(cid:2870)，对吗？ 138 二项式(cid:4672)2√x− (cid:2869) (cid:4673) (cid:2874) 的展开式中，所有项的二项式系数之和为64，对吗？ (cid:2934) 139 二项式(cid:4672)2√x− (cid:2869) (cid:4673) (cid:2874) 的展开式中，所有项系数之和为1，对吗？ (cid:2934) 设一组数据的平均数为x，方差为s(cid:2870)，在这组数据中加入一个新数据x后，则新数据的 140 方差会比原数据的方差要小，对吗？ 141 若随机变量X~N(2,σ²)，则P(X>2.5)=0.5−P(20，使得𝑓(−𝑥)=𝑓(𝑥)”是“𝑓(𝑥)为偶函数”的充要条件，对吗？ ✕，题目前半句是指存在关于y轴对称的点，需要改为“任意实数x”才是偶函数。 (cid:2869) 4.函数𝑦=𝑥+ 的最小值为2，对吗？ (cid:3051) ✕，因为𝑥可能为负数。 5.若一个函数存在极大值和极小值，则极大值一定大于极小值，对吗？ ✕，比如对勾函数。 6.函数𝑓(𝑥)=ln𝑥的零点是(1,0)，对吗？ ✕，零点是数，不是点。 7.方程 2(cid:3051) =𝑙𝑜𝑔 (cid:3117) 𝑥 只有一个解，对吗？ (cid:3118) ✓，转化为函数𝑦=2(cid:3051)和函数𝑦 =𝑙𝑜𝑔 (cid:3117) 𝑥只有一个交点即可。 (cid:3118) 8.直线𝑦=2和函数𝑦 =|2(cid:3051)−1|有2个交点，对吗？ ✕，函数有渐近线，如图，只有一个交点（别忘了数形结合）。 9.将函数𝑦 =2(cid:2879)(cid:3051)的图像向左平移2个单位后是𝑦 =2(cid:2879)(cid:3051)(cid:2878)(cid:2870)，对吗？ ✕，正确的平移结果为 𝑦=2(cid:2879)((cid:3051)(cid:2878)(cid:2870)) =2(cid:2879)(cid:3051)(cid:2879)(cid:2870) (cid:3051) 10.将函数𝑦 =𝑙𝑜𝑔 𝑥的图像向下平移2个单位后的图像与𝑦 =𝑙𝑜𝑔 (cid:4672) (cid:4673)的图像重合，对吗？ (cid:2870) (cid:2870) (cid:2872) (cid:3051) ✓，平移后变为𝑦=𝑙𝑜𝑔 𝑥−2=𝑙𝑜𝑔 𝑥−𝑙𝑜𝑔 4=𝑙𝑜𝑔 (cid:4672) (cid:4673) (cid:2870) (cid:2870) (cid:2870) (cid:2870) (cid:2872) 11.将点P(s,t)向右平移1个单位后的坐标为P(cid:4593)(s−1,t)，对吗？ ✕，函数的平移和点的平移有区别，向右平移一个单位后当然是P(cid:4593)(s+1,t). (cid:2869) 12.对于𝑚 ∈𝑅，直线𝑦 =𝑥+𝑚和函数𝑓(𝑥)= −𝑙𝑛𝑥−2𝑥永远不会相切，对吗？ (cid:3051) - 90 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}✓，因为， 𝑓(cid:4593)(𝑥)=− (cid:2869) − (cid:2869) −2<0，所以不可能存在斜率为正数的切线。 (cid:3051)(cid:3118) (cid:3051) 13.若 0<𝑎 <1, 𝑏 >1，则对数 𝑙𝑜𝑔 𝑏<0 ，对吗？ (cid:3028) ✓，根据对数图像即可知道正确。 14.对于正实数𝑎,𝑏，且 𝑎 ≠1, 𝑏 ≠1，恒有 𝑙𝑜𝑔 𝑏⋅𝑙𝑜𝑔 𝑎=1 ，对吗？ (cid:3028) (cid:3029) ✓，这是公式（别忘了换底公式） 15.对于定义域内任意𝑥，恒有𝑓(𝑥)=𝑓(2−𝑥)，则函数关于 𝑥 =1对称，对吗？ ✓，对称轴𝑥 =𝑎的定义式为： 𝑓(𝑥)=𝑓(2𝑎−𝑥) 16.对于定义域内任意𝑥，恒有𝑓(𝑥)+𝑓(2−𝑥)=4，则函数关于(1,2)对称，对吗？ ✓，对称中心(a,b)的定义式为：𝑓(𝑥)+𝑓(2𝑎−𝑥)=2𝑏 17.已知函数𝑓(𝑥)= (cid:2869) 𝑥(cid:2870)−2𝑥+𝑙𝑛𝑥，则𝑥 =1是函数的唯一极值点，对吗？ (cid:2870) ✕,𝑓(cid:4593)(𝑥)=𝑥−2+ (cid:2869) = ((cid:3051)(cid:2879)(cid:2869))(cid:3118) ≥0，原函数单增，无极值点。(不能单看𝑓(cid:4593)(1)=0) (cid:3051) (cid:3051) 18.函数𝑓(𝑥)=𝑥(cid:2870)−𝑎𝑥−2的零点一个比1大，一个比1小，则𝑎的范围是(−1,+∞)，对吗？ ✓，判别式𝛥=𝑎(cid:2870)+8>0，根据图像知道𝑓(1)<0即可，从而 𝑎 >−1 19.若𝑥 是函数𝑓(𝑥)=𝑥𝑒(cid:3051)−1的零点，则𝑥 也是函数𝑓(𝑥)=𝑥+𝑙𝑛𝑥的零点，对吗？ (cid:2868) (cid:2868) ✓，即𝑥 𝑒(cid:3051)(cid:3116) =1，变形为：𝑒(cid:3051)(cid:3116) = (cid:2869) ，两侧取对数得𝑙𝑛𝑒(cid:3051)(cid:3116) =𝑙𝑛 (cid:2869) ，即𝑥 =𝑙𝑛1−𝑙𝑛𝑥 (cid:2868) (cid:3051)(cid:3116) (cid:3051)(cid:3116) (cid:2868) (cid:2868) 即x +lnx =0，则x 也是函数f(x)=x+lnx的零点 (cid:2868) (cid:2868) (cid:2868) 其他思路：由x (cid:2868) e(cid:2934)(cid:3116) =1，即e(cid:2922)(cid:2924) (cid:3116)e(cid:2934)(cid:3116) =1，从而e(cid:2934)(cid:3116)(cid:2878)(cid:2922)(cid:2924)(cid:2934)(cid:3116) =e(cid:2868)，即x (cid:2868) +lnx (cid:2868) =0. 20.若𝑎|𝑎|>𝑏|𝑏|，则𝑎 >𝑏，对吗？ ✓，构造函数𝑓(𝑥)=𝑥|𝑥|，奇函数且单增，则𝑓(𝑎)>𝑓(𝑏)⇔𝑎 >𝑏 2(cid:3051),𝑥 ≤1 2(cid:3051),𝑥 <1 21.函数𝑓(𝑥)=(cid:3420) 与函数𝑔(𝑥)=(cid:3420) 的值域一样，对吗？ −𝑥+1,𝑥 >1 −𝑥+1,𝑥 ≥1 ✕，看图知：𝑓(𝑥)的值域为 (−∞,0)∪(0,2] ,𝑔(𝑥)的值域为 (−∞,2]。 - 91 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}(cid:2869) 22.已知对勾函数𝑓(𝑥)=𝑥+ ，直线𝑦 =𝑚(𝑚∈𝑅)和𝑓(𝑥)相交于A,B两点，则𝑥 ⋅𝑥 为定值，对吗？ (cid:3051) (cid:3002) (cid:3003) ✓，即方程𝑥+ (cid:2869) =𝑚的根为𝑥 ,𝑥 ，变形为：𝑥(cid:2870)+1=𝑚𝑥，即方程𝑥(cid:2870)−𝑚𝑥+1=0的根为𝑥 ,𝑥 ，由韦达定 (cid:3051) (cid:3002) (cid:3003) (cid:3002) (cid:3003) 理得𝑥 ⋅𝑥 =1，故为定值。 (cid:3002) (cid:3003) 23.函数𝑓(𝑥)=𝑒(cid:3051)⋅𝑙𝑛𝑥是定义域上的单增函数，对吗？ ✓，因为𝑓(cid:4593)(𝑥)=𝑒(cid:3051)(cid:4672)𝑙𝑛𝑥+ (cid:2869) (cid:4673)，设𝑔(𝑥)=𝑙𝑛𝑥+ (cid:2869) ,𝑔(cid:4593)(𝑥)= (cid:2869) − (cid:2869) = (cid:3051)(cid:2879)(cid:2869) ，所以𝑔(𝑥)在(0,1)上单减，在(1,+∞) (cid:3051) (cid:3051) (cid:3051) (cid:3051)(cid:3118) (cid:3051)(cid:3118) 上单增，故𝑔(𝑥) =𝑔(1)=1>0，即𝑔(cid:4593)(𝑥)>0，所以𝑓(cid:4593)(𝑥)>0，因此𝑓(𝑥)=𝑒(cid:3051)⋅𝑙𝑛𝑥单增。 (cid:3040)(cid:3036)(cid:3041) 24.增函数+增函数=增函数，增函数×增函数=增函数，对吗？ 前半句✓，后半句✕。比如𝑓(𝑥)=𝑥⋅𝑒(cid:3051)，通过求导得到函数在(−∞,−1)上单减，在(−1,∞)上单增。 25.过坐标原点作函数𝑓(𝑥)=𝑒(cid:3051)+𝑥的切线，则切线的斜率为𝑒+1，对吗？ ✓，特别注意切点不是原点。（求切线方程时，一定要注意是“过”点，还是“在”点）设切点P(x ,y )，因此： (cid:2868) (cid:2868) k =f(cid:4593)(x )=e(cid:2934)(cid:3116) +1 (cid:2868) (cid:3422)k = (cid:2935)(cid:3116)(cid:2879)(cid:2868) ⇒𝑥 =1,𝑘 =𝑒+1。 (cid:2934)(cid:3116)(cid:2879)(cid:2868) (cid:2868) y =e(cid:2934)(cid:3116) +x (cid:2868) (cid:2868) (cid:2869) 26.对于m∈R，直线𝑦 =𝑥+𝑚和函数𝑓(𝑥)= −𝑙𝑛𝑥−2𝑥永远不会相切，对吗？ (cid:3051) ✓，因为，𝑓(cid:4593)(𝑥)=− (cid:2869) − (cid:2869) −2<0，所以不可能存在斜率为正数的切线。 (cid:3051)(cid:3118) (cid:3051) 27.设𝑓(𝑥)=𝑎𝑥(cid:2870)−2𝑥+1，若对∀𝑥 ,𝑥 ∈(−1,+∞)，且x ≠x ，都有 (cid:3033)((cid:3051)(cid:3117) )(cid:2879)(cid:3033)((cid:3051)(cid:3118) ) <0成立，则𝑎的取值范围 (cid:2869) (cid:2870) (cid:2869) (cid:2870) (cid:3051)(cid:3117)(cid:2879)(cid:3051)(cid:3118) 为𝑎 ≥−1，对吗？ ✕，特别注意本题没有说是二次函数，题意为函数在区间(−1,+∞)上为减函数，①若a=0，则函数在定义 (cid:2869) 域上都是单减函数，符合题意；②若a≠0，则该二次函数开口向下a<0，且对称轴x= ≤−1，故正确答 (cid:2911) 案为：[−1,0] 28.设函数𝑓(𝑥)满足：若对∀𝑥 ,𝑥 ∈𝑅，且𝑥 ≠𝑥 ，都有 (cid:3033)((cid:3051)(cid:3117) )(cid:2879)(cid:3033)((cid:3051)(cid:3118) ) >𝑎，则𝑦=𝑓(𝑥)−𝑎𝑥是增函数，对吗？ (cid:2869) (cid:2870) (cid:2869) (cid:2870) (cid:3051)(cid:3117)(cid:2879)(cid:3051)(cid:3118) ✓，这是结论，证明如下：设x >x ，则有f(x )−f(x )>a(x −x )⇒f(x )−ax >f(x )−ax ,引入g(x)= (cid:2869) (cid:2870) (cid:2869) (cid:2870) (cid:2869) (cid:2870) (cid:2869) (cid:2869) (cid:2870) (cid:2870) f(x)−ax，即当x >x 时，有g(x )>g(x )，故为增函数。 (cid:2869) (cid:2870) (cid:2869) (cid:2870) 同理x 𝑏，对吗？ (cid:3117) (cid:2869)(cid:2868) (cid:3117) (cid:2869)(cid:2868) ✓，方法一：高次方。不难得到a,b均大于1.所以a(cid:2869)(cid:2868) =(cid:4672)2(cid:3118)(cid:4673) =2(cid:2873) =32, b(cid:2869)(cid:2868) =(cid:4672)5(cid:3121)(cid:4673) =5(cid:2870) =25，所以a>b 方法二:取对数。lna=ln2 (cid:3117) (cid:3118) = (cid:2869) ln2= (cid:2922)(cid:2924)(cid:2870)，同理得lnb= (cid:2922)(cid:2924) ，结合上面的作差法即可得出结果。 (cid:2870) (cid:2870) (cid:2873) (cid:3039)(cid:3041)(cid:2870) (cid:3039)(cid:3041)(cid:2873) 30.设 𝑎 = , 𝑏 = ，则𝑎 >𝑏，对吗？ (cid:2870) (cid:2873) (cid:2922)(cid:2924)(cid:2870) (cid:2922)(cid:2924)(cid:2873) (cid:2873)(cid:2922)(cid:2924)(cid:2870)(cid:2879)(cid:2870)(cid:2922)(cid:2924)(cid:2873) (cid:2922)(cid:2924)(cid:2871)(cid:2870)(cid:2879)(cid:2922)(cid:2924)(cid:2870)(cid:2873) ✓，作差法。a−b= − = = >0 (cid:2870) (cid:2873) (cid:2869)(cid:2868) (cid:2869)(cid:2868) 31.设𝑎 =𝑠𝑖𝑛1,𝑏 =𝑠𝑖𝑛2,𝑐 =𝑠𝑖𝑛3，则𝑏 >𝑎 >𝑐，对吗？ ✓，将弧度制转化成角度制1= (cid:2869)(cid:2876)(cid:2868)∘ ≈57.3∘,(要了解这里的π约等于3.14) (cid:2976) 32.设𝑓(𝑥)是定义在R上的偶函数，若𝑓(𝑥 )=𝑓(𝑥 )且𝑥 ≠𝑥 ，则𝑥 +𝑥 =0，对吗？ (cid:2869) (cid:2870) (cid:2869) (cid:2870) (cid:2869) (cid:2870) ✕，和函数的周期性有关，比如：f(x)=cosx中有f(0)=f(2π) 33.设函数𝑓(𝑥)=𝑎𝑥(cid:2871)+𝑏𝑥(cid:2870)+𝑐𝑥+𝑑(𝑎 ≠0)，则存在实数𝑎,𝑏,𝑐,𝑑，使得函数𝑓(𝑥)存在唯一极值点，对吗？ ✕,𝑓(cid:4593)(𝑥)=3𝑎𝑥(cid:2870)+2𝑏𝑥+𝑐(𝑎 ≠0)是二次函数，①Δ≤0时，原函数单增无极值点；②Δ>0时，原函数有 2 个极值点。不可能是1个。 34.已知函数𝑓(𝑥)=2(cid:3051)−2(cid:2879)(cid:3051)−2，则不等式𝑓(𝑥)> (cid:2875) 的解集为(2,+∞)，对吗？ (cid:2872) ✓，即2(cid:2934)−2(cid:2879)(cid:2934) > (cid:2869)(cid:2873) , g(x)=2(cid:2934)−2(cid:2879)(cid:2934)是奇函数且是单增函数，g(2)= (cid:2869)(cid:2873) ，故正确。 (cid:2872) (cid:2872) 35.若𝑎 >𝑏 >𝑐，则𝑎+𝑏 >𝑐，对吗？ a>c ✕，如a=−1, b=−2,c=−3，但a+b>2c是对的。(不等式加法(cid:4676) ⇒a+b>2c) b>c 二、向量 36.零向量和任意向量都平行，对吗？ ✓，这是教材规定。 37.若向量𝑎⃗//𝑏(cid:4652)⃗,𝑏(cid:4652)⃗//𝑐⃗，则𝑎⃗//𝑐⃗，对吗？ ✕，因为b(cid:4652)⃗可能是零向量，则a(cid:4652)⃗,c⃗可能不平行 38.对于两个不共线的向量𝑎⃗,𝑏(cid:4652)⃗，若𝑎⃗+2𝑏(cid:4652)⃗ =𝑥𝑎⃗+𝑦𝑏(cid:4652)⃗，则𝑥 =1,𝑦=2，对吗？ ✓，如果去掉“不共线”三个字，就是错的。 - 93 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}39.对于两个非零向量𝑎⃗,𝑏(cid:4652)⃗，若𝑎⃗(cid:2870) =𝑎⃗⋅𝑏(cid:4652)⃗，则𝑎⃗ =𝑏(cid:4652)⃗，对吗？ ✕，向量不能约分，由a(cid:4652)⃗(cid:2870) =a(cid:4652)⃗⋅(cid:4652)b⃗得到的是a(cid:4652)⃗⊥a(cid:4652)⃗−(cid:4652)b⃗或a(cid:4652)⃗=b(cid:4652)⃗ 40.对于两个向量𝑎⃗,𝑏(cid:4652)⃗,(cid:3435)𝑎⃗⋅𝑏(cid:4652)⃗(cid:3439) (cid:2870) 和𝑎⃗(cid:2870)⋅𝑏(cid:4652)⃗(cid:2870)的运算结果是一样的，对吗？ (cid:2870) (cid:2870) (cid:2870) ✕,(cid:3435)a(cid:4652)⃗⋅(cid:4652)b⃗(cid:3439) =(cid:3435)|a(cid:4652)⃗|⋅(cid:3627)b(cid:4652)⃗(cid:3627)cosθ(cid:3439) =|a(cid:4652)⃗|(cid:2870)⋅(cid:3627)b(cid:4652)⃗(cid:3627) cos(cid:2870)θ，因此不一样。 41.将(cid:3627)𝑎⃗+𝑏(cid:4652)⃗(cid:3627)平方后展开得到(cid:3627)𝑎⃗+𝑏(cid:4652)⃗(cid:3627) (cid:2870) =𝑎⃗(cid:2870)+𝑏(cid:4652)⃗(cid:2870)+2𝑎⃗⋅𝑏(cid:4652)⃗，对吗？ ✓，这是向量运算中常用到的公式。 42.向量𝑎⃗ =(𝑥 ,𝑦 )和向量𝑏(cid:4652)⃗ =(𝑥 ,𝑦 )共线，则有 (cid:3051)(cid:3117) = (cid:3052)(cid:3117)成立，对吗？ (cid:2869) (cid:2869) (cid:2870) (cid:2870) (cid:3051)(cid:3118) (cid:3052)(cid:3118) ✕，共线是x y =x y ，虽然交叉相乘后结果一样，但是✕。比如a(cid:4652)⃗=(1,0),b(cid:4652)⃗=(2,0) (cid:2869) (cid:2870) (cid:2870) (cid:2869) 43.向量的平方等于其模长的平方，复数也满足，即𝑎⃗(cid:2870) =|𝑎⃗|(cid:2870),𝑧(cid:2870) =|𝑧|(cid:2870)，对吗？ 前半句✓，后半句✕。向量满足，复数不满足。比如(1+i)(cid:2870) =−2i，而|1+i|(cid:2870) =2 44.若𝑎⃗ =(1,−2),𝑏(cid:4652)⃗=(𝑥,4)，若平面内任意向量𝑐⃗，都存在实数𝜆,𝜇，使得𝑐⃗=𝜆𝑎⃗+𝜇𝑏(cid:4652)⃗成立，则𝑥 ≠−2，对 吗？ ✓，平面向量基本定理，也就是a(cid:4652)⃗=(1,−2),b(cid:4652)⃗=(x,4)是基底向量(不共线) 45.已知|𝑎⃗|=2(cid:3627)𝑏(cid:4652)⃗(cid:3627)=2,(cid:3451)𝑎⃗,𝑏(cid:4652)⃗(cid:3455)=60∘，则(cid:3627)𝑎⃗+𝑏(cid:4652)⃗(cid:3627)=7，对吗？ ✕，首先审题看仔细，不要读成了“|𝑎⃗|=2,(cid:3627)𝑏(cid:4652)⃗(cid:3627)=2”，根据平方：(cid:3627)a(cid:4652)⃗+(cid:4652)b⃗(cid:3627) (cid:2870) =a(cid:4652)⃗(cid:2870)+(cid:4652)b⃗(cid:2870)+2(cid:4652)a⃗b(cid:4652)⃗=4+1+2×2× 1×cos60∘ =7，所以(cid:3627)a(cid:4652)⃗+(cid:4652)b⃗(cid:3627)=√7，别忘了开根号! 46.在ΔABC中，点P在𝐵𝐶的延长线上，设𝐴(cid:4652)(cid:4652)(cid:4652)(cid:4652)𝑃(cid:4652)⃗ =𝑥𝐴(cid:4652)(cid:4652)(cid:4652)(cid:4652)𝐵(cid:4652)⃗+𝑦𝐴(cid:4652)(cid:4652)(cid:4652)(cid:4652)𝐶(cid:4652)⃗，则𝑥+𝑦 =1，且𝑥 <0,𝑦 >0,对吗？ ✓，系数和为1是结论。 (cid:2870) (cid:2870) (cid:2870) 47.已知空间中四点坐标分别为𝐴(1,0,1),𝐵(1,1,0),𝐶(0,1,1),𝐷(cid:4672) , ,𝑎(cid:4673)，则𝑎 = 时，点D在平面ABC内，对吗？ (cid:2871) (cid:2871) (cid:2871) 对！（1）即存在实数x,y，使得A(cid:4652)(cid:4652)(cid:4652)(cid:4652)D(cid:4652)⃗=xA(cid:4652)(cid:4652)(cid:4652)(cid:4652)B(cid:4652)⃗+y(cid:4652)A(cid:4652)(cid:4652)(cid:4652)(cid:4652)C⃗成立，化简推算可以分别求出x,y,a; （2）求出平面ABC的法向量m(cid:4652)(cid:4652)(cid:4652)⃗，利用m(cid:4652)(cid:4652)(cid:4652)⃗⋅(cid:4652)A(cid:4652)(cid:4652)(cid:4652)D(cid:4652)⃗=0即可求出的值。 48.设𝑎⃗ =(−1,2),𝑏(cid:4652)⃗ =(2,𝑥)，若为(cid:3451)𝑎⃗,𝑏(cid:4652)⃗(cid:3455)钝角，则𝑥的取值范围是(−∞,1)，对吗？ ✕, （1）从画图层面看：找到直角时𝑥 =1，反向时𝑥 =−4，所以x<1且x≠−4 （2）从运算层面看：钝角翻译为𝑎⃗⋅𝑏(cid:4652)⃗ <0且𝑎⃗,𝑏(cid:4652)⃗不反向，所以a(cid:4652)⃗⋅(cid:4652)b⃗=−2+2x<0且a(cid:4652)⃗,b(cid:4652)⃗不反向(即x≠−4) - 94 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}49.设平面α的法向量为m(cid:4652)(cid:4652)(cid:4652)⃗, A是平面α内任意一点，P是平面α外一点，则点P到平面α的距离公式为𝑑 = (cid:3002)(cid:4652)(cid:4652)(cid:4652)(cid:4652)(cid:3017)(cid:4652)⃗⋅(cid:3040)(cid:4652)(cid:4652)(cid:4652)⃗， |(cid:3040)(cid:4652)(cid:4652)(cid:4652)⃗| 对吗？ ✕。正确公式为：d= (cid:3627)(cid:2885)(cid:4652)(cid:4652)(cid:4652)(cid:4652)(cid:2900)(cid:4652)⃗⋅(cid:2923)(cid:4652)(cid:4652)(cid:4652)⃗(cid:3627) |(cid:2923)(cid:4652)(cid:4652)(cid:4652)⃗| 50.已知ΔABC是一个边长为2的等边三角形，则A(cid:4652)(cid:4652)(cid:4652)(cid:4652)B(cid:4652)⃗⋅B(cid:4652)(cid:4652)(cid:4652)(cid:4652)C(cid:4652)⃗=2，对吗？ ✕.A(cid:4652)(cid:4652)(cid:4652)(cid:4652)B(cid:4652)⃗与B(cid:4652)(cid:4652)(cid:4652)(cid:4652)C(cid:4652)⃗的夹角为120∘，不是60∘!正确是：A(cid:4652)(cid:4652)(cid:4652)(cid:4652)B(cid:4652)⃗⋅(cid:4652)B(cid:4652)(cid:4652)(cid:4652)(cid:4652)C⃗=2×2×cos120∘ =−2 51.设O为等边三角形ΔABC的中心，D为BC的中点，则O(cid:4652)(cid:4652)(cid:4652)(cid:4652)A(cid:4652)⃗+O(cid:4652)(cid:4652)(cid:4652)(cid:4652)B(cid:4652)⃗+O(cid:4652)(cid:4652)(cid:4652)(cid:4652)C(cid:4652)⃗=0(cid:4652)⃗，且 A(cid:4652)(cid:4652)(cid:4652)(cid:4652)O(cid:4652)⃗=2O(cid:4652)(cid:4652)(cid:4652)(cid:4652)D(cid:4652)⃗，对吗？ 对。这是结论(三角形重心，即有A(cid:4652)(cid:4652)(cid:4652)(cid:4652)O(cid:4652)⃗=2O(cid:4652)(cid:4652)(cid:4652)(cid:4652)D(cid:4652)⃗) 三、三角函数与解三角 52.若𝑡𝑎𝑛(𝛼+𝛽)=𝑡𝑎𝑛𝛼+𝑡𝑎𝑛𝛽，则𝑡𝑎𝑛𝛼⋅𝑡𝑎𝑛𝛽 =0，对吗？ (cid:2976) (cid:2976) (cid:2930)(cid:2911)(cid:2924)(cid:2961)(cid:2878)(cid:2930)(cid:2911)(cid:2924)(cid:2962) ✕，比如α= ,β=− .根据tan(α+β)= =tanα+tanβ,则tanα⋅tanβ=0或tanα+tanβ=0(注意： (cid:2872) (cid:2872) (cid:2869)(cid:2879)(cid:2930)(cid:2911)(cid:2924)(cid:2961)(cid:2930)(cid:2911)(cid:2924)(cid:2962) 不能习惯性约分！) 53.已知𝑠𝑖𝑛𝑥 =𝑡𝑎𝑛𝑥，则𝑐𝑜𝑠𝑥 =1一定成立，对吗？ (cid:2929)(cid:2919)(cid:2924)(cid:2934) ✕，由sinx=tanx= ，应该是sinx=0或cosx=1，因此得到是cosx=1或-1. (cid:2913)(cid:2925)(cid:2929)(cid:2934) (cid:2976) 54.函数𝑦 =𝑡𝑎𝑛𝑥的一个对称中心是(cid:4672) ,0(cid:4673)，对吗？ (cid:2870) (cid:2921)(cid:2976) (cid:2976) ✓，y=tanx的对称中心为(cid:4672) ,0(cid:4673)(k∈Z)，所以(cid:4672) ,0(cid:4673)是其中一个。注意到对称中心不一定在函数图像上哦， (cid:2870) (cid:2870) 比如反比例函数关于原点对称。 (cid:3095) (cid:2976) 55.函数𝑓(𝑥)=𝑠𝑖𝑛(cid:4672)𝜔𝑥+ (cid:4673)的两条对称轴之间的距离最小值为 ，则ω=2，对吗？ (cid:2872) (cid:2870) - 95 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}(cid:2904) (cid:2976) ✕，两条对称轴之间的距离最小值应该是半个周期，即 = ，正确的应该是ω=±2. (cid:2870) (cid:2870) (cid:3095) 56.设函数𝑓(𝑥)=𝑠𝑖𝑛(cid:2872)𝑥+𝑐𝑜𝑠(cid:2870)𝑥，则函数关于𝑥 = 对称，对吗？ (cid:2872) (cid:2976) (cid:2976) ✓，如果满足：f(cid:4672) −x(cid:4673)=f(x)，则函数关于x= 对称 (cid:2870) (cid:2872) 又f(cid:4672) (cid:2976) −x(cid:4673)=sin(cid:2872)(cid:4672) (cid:2976) −x(cid:4673)+cos(cid:2870)(cid:4672) (cid:2976) −x(cid:4673)=cos(cid:2872)x+sin(cid:2870)x=(cos(cid:2870)x)(cid:2870)+sin(cid:2870)x (cid:2870) (cid:2870) (cid:2870) =(1−sin(cid:2870)x)(cid:2870)+sin(cid:2870)x=1+sin(cid:2872)x−2sin(cid:2870)x+sin(cid:2870)x=sin(cid:2872)x+1−sin(cid:2870)x=sin(cid:2872)x+cos(cid:2870)x=f(x)，因此正确 (cid:2976) (cid:2873)(cid:2976) 57.已知f(x)=√3sin(2x+φ)(0<φ<π)的图像如下，则φ= 或 ，对吗？ (cid:2874) (cid:2874) ✕，带入点(cid:4672)0, √(cid:2871) (cid:4673)中，则√3sinφ= √(cid:2871) ⇒sinφ= (cid:2869) (cid:2870) (cid:2870) (cid:2870) 又0<φ<π，得φ= (cid:2976) 或 (cid:2873)(cid:2976) ，看图知：(cid:4672)0, √(cid:2871) (cid:4673)位于减区间内 (cid:2874) (cid:2874) (cid:2870) 故f(cid:4593)(0)<0，故舍去φ= (cid:2976) ，因此答案为φ= (cid:2873)(cid:2976) (cid:2874) (cid:2874) 58.∃x∈R，使得sinx+cosx=2，对吗？ (cid:2976) ✕，因为sinx+cosx=√2sin(cid:4672)x+ (cid:4673)，所以最大为√2，不可能取得到2。 (cid:2872) 59.函数𝑓(𝑥)=𝑠𝑖𝑛𝑥+𝑐𝑜𝑠𝑥+2𝑠𝑖𝑛𝑥𝑐𝑜𝑠𝑥，则函数的最大值为√2+1，对吗？ (cid:2976) ✓，方法一：拆分函数f(x)=√2sin(cid:4672)x+ (cid:4673)+sin2x，函数前半部分的最大值为√2，后半部分的最大值为 1， (cid:2872) (cid:2976) 且可以找到同一个x= 取得，因此正确。 (cid:2872) 方法二：换元法设t=sinx+cosx⇒t(cid:2870) =1+2sinxcosx，故2sinxcosx=t(cid:2870)−1 从而f(x)=t+t(cid:2870)−1,t∈(cid:3427)−√2,√2(cid:3431)，根据二次函数即可求最值. (cid:3095) 60.将函数𝑓(𝑥)=𝑡𝑎𝑛(cid:4672)2𝑥+ (cid:4673)的最小正周期为𝜋，对吗？ (cid:2871) - 96 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}(cid:2976) (cid:2976) ✕，正切型函数的最小正周期公式为T= ，故最小正周期为 |(cid:2985)| (cid:2870) 61.设函数𝑓(𝑥)=𝑠𝑖𝑛2𝜔𝑥+𝑐𝑜𝑠2𝜔𝑥(𝜔 >0)的最小正周期为π，则ω=2，对吗？ (cid:2976) (cid:2870)(cid:2976) ✕,f(x)=√2sin(cid:4672)2ωx+ (cid:4673)，注意本题中应该是T= =π，此时ω=1. (cid:2872) |(cid:2870)(cid:2985)| 62.函数𝑓(𝑥)=𝑐𝑜𝑠(cid:2872)𝑥−𝑠𝑖𝑛(cid:2872)𝑥的最正周期为π，对吗？ ✓，f(x)=(cos(cid:2870)x−sin(cid:2870)x)(cos(cid:2870)x+sin(cid:2870)x)=cos(cid:2870)x−sin(cid:2870)x=cos2x，故T= (cid:2870)(cid:2976) =π (cid:2870) (cid:2976) 63.函数𝑓(𝑥)=𝑐𝑜𝑠(cid:2872)𝑥+𝑠𝑖𝑛(cid:2872)𝑥的最正周期为 ，对吗？ (cid:2870) ✓，f(x)=(sin(cid:2870)x+cos(cid:2870)x)(cid:2870)−2sin(cid:2870)xcos(cid:2870)x=1− (cid:2869) sin(cid:2870)2x，又sin(cid:2870)2x= (cid:2869) (1−cos4x), (cid:2870) (cid:2870) (cid:2869) (cid:2871) (cid:2870)(cid:2976) (cid:2976) 所以f(x)= cos4x+ ，故T= = (cid:2872) (cid:2872) (cid:2872) (cid:2870) (cid:2976) (cid:2873)(cid:2976) 64.函数y=sin(cid:4672)2x− (cid:4673)和函数y=cos(cid:4672)2x− (cid:4673)的图像是重合的，对吗？ (cid:2871) (cid:2874) ✓，简单粗暴将其展开，即y=sin(cid:4672)2x− (cid:2976) (cid:4673)= (cid:2869) sin2x− √(cid:2871) cos2x (cid:2871) (cid:2870) (cid:2870) y=cos(cid:4672)2x− (cid:2873)(cid:2976) (cid:4673)=− √(cid:2871) cos2x+ (cid:2869) sin2x，二者一模一样。(也可以运用诱导公式证明) (cid:2874) (cid:2870) (cid:2870) (cid:2976) (cid:3095) (cid:3095) 65.点(cid:4672) ,0(cid:4673)是函数𝑦 =2𝑠𝑖𝑛(cid:4672)2𝑥− (cid:4673)和函数𝑦 =2𝑐𝑜𝑠(cid:4672)2𝑥+ (cid:4673)−1的共同的对 (cid:2874) (cid:2871) (cid:2874) 称中心，对吗？ (cid:2976) ✕，注意到y=2cos(cid:4672)2x+ (cid:4673)−1的对称中心的纵坐标不是0，应该是-1 (cid:2874) 66.函数f(x)=|sinx+cosx|和函数g(x)=2cos(cid:2870)x−2的最小正周期都是π，对吗？ (cid:2976) (cid:2976) ✓，f(x)=(cid:4698)√2sin(cid:4672)x+ (cid:4673)(cid:4698),g(x)=cos2x−1，y=√2sin(cid:4672)x+ (cid:4673)由的最小正周期为2π，则将位于x轴下方翻 (cid:2872) (cid:2872) 折到x轴上方后得f(x)，故f(x)的最小正周期是π，显然g(x)=cos2x−1的最小正周期是π (cid:2976) 67.将函数f(x)=sin(cid:4672)2x+ (cid:4673)向左平移m(m>0)个单位后图形与f(x)重合，则m的最小值为π，对吗？ (cid:2871) ✓，因为函数的最小正周期为π，向左平移最小正周期的整数倍个单位图像都是重合的。 (cid:3095) (cid:3095) 68.已知函数𝑓(𝑥)=𝑠𝑖𝑛(cid:4672)𝜔𝑥+ (cid:4673)(𝜔 >0)，若对于任意实数x，都有𝑓(𝑥)≤𝑓(cid:4672) (cid:4673)成立，则ω的最小值为 1， (cid:2874) (cid:2871) - 97 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}对吗？ (cid:2976) (cid:2976) (cid:2976)(cid:2985) (cid:2976) (cid:2976)(cid:2985) (cid:2976) (cid:2976) ✓，翻译后即：函数 f(x)在 x= 处取得最大值，即f(cid:4672) (cid:4673)=1,从而sin(cid:4672) + (cid:4673)=1，所以 + = + (cid:2871) (cid:2871) (cid:2871) (cid:2874) (cid:2871) (cid:2874) (cid:2870) 2kπ(k∈Z)，即ω=1+6k(k∈Z)，故正确。 69.存在ΔABC，使得A=2B和𝑎 =2𝑏同时成立，对吗？ ✕,A=2B⇒sinA=sin2B=2sinBcosB⇒a=2bcosB,若a=2 b，则cosB=1，又B∈(0,π)，不可能成立， 因此不存在这样的ΔABC。 70.在ΔABC中，A>B是sinA>sinB成立的充要条件，对吗？ ✓，根据大角对大边，则有A>B⇔a>b，由正弦定理有a>b⇔sinA>sinB 71.在ΔABC中，A>B是cosA0，则ΔABC为锐角三角形，对吗？ ✓，在三角形中：钝角tan值为负，锐角tan值为正，根据tanAtanBtanC>0，因此 tanA,tanB,tanC中必然都是正，因此均为锐角。 (cid:2869) 77.一个腰长为1的等腰三角形，面积最大值为 ，对吗？ (cid:2870) (cid:2869) (cid:2869) ✓，根据三角形面积公式S= ×1×1×sinθ，故等腰直角时取得最大值为 . (cid:2870) (cid:2870) (cid:2869) (cid:2976) 78.若△ABC的面积满足𝑆 = 𝑎𝑐，则B= ，对吗？ (cid:2872) (cid:2874) - 98 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}(cid:2869) (cid:2869) (cid:2976) (cid:2873)(cid:2976) ✕，根据面积公式S= acsinB，则sinB= ，则B= 或B= (cid:2870) (cid:2870) (cid:2874) (cid:2874) 79.已知ΔABC中，𝑎 =3, 𝑏 =7,𝑐 =8，则ΔABC为钝角三角形，对吗？ ✓，最大角为C，且cosC= (cid:2911)(cid:3118)(cid:2878)(cid:2912)(cid:3118)(cid:2879)(cid:2913)(cid:3118) = (cid:2877)(cid:2878)(cid:2872)(cid:2877)(cid:2879) <0，因此是钝角三角形。 (cid:2870)(cid:2911)(cid:2912) (cid:2870)×(cid:2871)×(cid:2875) (cid:2976) 80.已知ΔABC中，𝑎 =3, 𝑏 =7,𝑐 =8，则A< ，对吗？ (cid:2874) ✓，因为cosA= (cid:2912)(cid:3118)(cid:2878)(cid:2913)(cid:3118)(cid:2879)(cid:2911)(cid:3118) = (cid:2872)(cid:2877)(cid:2878)(cid:2874)(cid:2872)(cid:2879)(cid:2877) = (cid:2869)(cid:2871) > √(cid:2871)，即cosA>cos (cid:2976) ，根据y=cosx在(0,2)是减函数，所以A< (cid:2976) (cid:2870)(cid:2912)(cid:2913) (cid:2870)×(cid:2875)×(cid:2876) (cid:2869)(cid:2872) (cid:2870) (cid:2874) (cid:2874) 四、数列 81.存在等差数列的前n项和S 也是等差数列，对吗？ (cid:2924) ✓，比如a =1时，S =n (cid:2924) (cid:2924) 82.对于任意一个等差数列，都有𝑎 +𝑎 =𝑎 成立，对吗？ (cid:2869) (cid:2876) (cid:2877) ✕，等差性质的运用要保证等式左右项数一致才可以，如a +a =a +a 是正确的 (cid:2869) (cid:2876) (cid:2871) (cid:2874) 83.对于任意m,n∈N∗，都有a =a +a ，则是等差数列，对吗？ (cid:2923)(cid:2878)(cid:2924) (cid:2924) (cid:2923) ✓，不妨令m=1，则a =a +a ，即a −a =a =常数。 (cid:2924)(cid:2878)(cid:2869) (cid:2924) (cid:2869) (cid:2924)(cid:2878)(cid:2869) (cid:2924) (cid:2869) 84.若𝑎 是等差数列，则𝑎 ,𝑎 ,𝑎 ,⋯,𝑎 ,𝑎 也是等差数列，且共有n+1项，对吗？ (cid:3041) (cid:2870) (cid:2873) (cid:2876) (cid:2871)(cid:3041)(cid:2879)(cid:2869) (cid:2871)(cid:3041)(cid:2878)(cid:2870) ✓，看下标的通项是3n−1，则第n项是a ，因此n+1共项。 (cid:2871)(cid:2924)(cid:2879)(cid:2869) 85.存在等比数列的前n项和S 是等差数列，对吗？ (cid:2924) ✓，比如a =1时，S =n。 (cid:2924) (cid:2924) 86.对于一个数列，每一项都是前一项的2倍，则数列为等比数列，对吗？ ✕,比如数列首项是0。 87.对于等比数列{a }满足：𝑎 =2𝑎 ，则公比q是2吗？ (cid:2924) (cid:3041) (cid:3041)(cid:2878)(cid:2869) (cid:2869) ✕，看清楚，公比是 。 (cid:2870) 88.等比数列中任意一项都不为0，且公比也不为0，对吗？ ✓，注意到公比是指数列后一项和前一项的比值 89.等比数列如果是单调数列，则该等比数列的公比q>0且q≠1，对吗？ ✓，单增：a >0,q>1或a <0,00,01。 (cid:2869) (cid:2869) (cid:2869) (cid:2869) 90.等比数列的前5项分别为1,𝑎 ,𝑎 ,𝑎 ,𝑎 ,16，则𝑎 =±4，对吗？ (cid:2869) (cid:2870) (cid:2871) (cid:2872) (cid:2871) - 99 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}✕.根据a(cid:2870) =a a =16，且a ,a ,a 符号一致，故a =4 (cid:2871) (cid:2869) (cid:2873) (cid:2869) (cid:2871) (cid:2873) (cid:2871) 91.对于任意m,n∈N∗，都有𝑎 =𝑎 ⋅𝑎 ，则是等比数列，对吗？ (cid:3040)(cid:2878)(cid:3041) (cid:3041) (cid:3040) ✕,比如全为0的数列。但如果首项不为0时，是对的，证明思路同上面。 92.设数列{𝑎 }与数列{𝑏 }均为等比数列，则{𝑎 ⋅𝑏 }也是等比数列，对吗？ (cid:3041) (cid:3041) (cid:3041) (cid:3041) ✓，因为按等比数列定义有： (cid:2911)(cid:3172)⋅(cid:2912)(cid:3172) = (cid:2911)(cid:3172) ⋅ (cid:2912)(cid:3172) =常数 (cid:2911)(cid:3172)(cid:3127)(cid:3117)⋅(cid:2912)(cid:3172)(cid:3127)(cid:3117) (cid:2911)(cid:3172)(cid:3127)(cid:3117) (cid:2912)(cid:3172)(cid:3127)(cid:3117) 93.已知数列𝑎 =𝑛(cid:2870)−11𝑛+2，则当n= (cid:2869)(cid:2869) 时，𝑎 取得最小值，对吗？ (cid:3041) (cid:2870) (cid:3041) ✕，注意到数列里n∈N∗，因此n=5或n=6时取得最小值。 五、立体几何 94.正四面体一定是正三棱锥，对吗？ ✓，正四面体是所有棱长都相等的三棱锥，正三棱锥是底面为等边三角形且定点在底面的投影是底面中心。 因此正四面体是正三棱锥，但正三棱锥不一定是正四面体。 95.异面直线是既不平行也不相交的直线，对吗？ ✓，异面直线的概念就是既不平行也不相交的直线。 96.直线l//直线m，且m⊂平面α，则1//平面α，对吗？ ✕，因为l可能在平面α内。（这是同学们在判断线面平时最容易犯的错！） 97.如果一条直线的方向向量和一个平面的法向量垂直，则该直线平行于平面，对吗？ ✕，因为直线也可能在平面内。 98.若平面α⊥平面β，直线l⊥平面α，则l//平面β，对吗？ ✕，因为l可能在平面β内。 99.若平面α⊥平面β,α∩β=m，直线l⊥m，且l⊂α，则l⊥平面β，对吗？ ✓，一般的，若已知面面垂直，往往就是需要这一招转化成线面垂直。 100.一个三棱锥可以每一个面都是直角三角形，对吗？ ✓，如图所示。 - 100 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}101. 圆锥的侧面展开图是半圆时，其母线与底面夹角为60°，对吗？ ✓，展开图半圆对应母线长 𝑙 =2𝑟，夹角为 60∘ 102. 正方体的外接球体积与内切球体积之比为 3√3，对吗？ ✓，外接球半径 𝑅 = √(cid:2871)(cid:3028)，内切球半径 𝑟 = (cid:3028) ，体积比为 (cid:3435)√3(cid:3439) (cid:2871) =3√3 (cid:2870) (cid:2870) 103.棱台体积公式仅适用于正棱台，对吗？ (cid:2869) ✕，任何棱台均可使用 𝑉 = ℎ(cid:3435)𝑆 +(cid:3493)𝑆 𝑆 +𝑆 (cid:3439)，与是否正棱台无关 (cid:2869) (cid:2869) (cid:2870) (cid:2870) (cid:2871) 104.二面角的夹角与其法向量夹角的余弦值相等，对吗？ ✕，二面角的夹角余弦值等于法向量夹角余弦的绝对值。 六、直线与圆的方程 105.直线 𝑦 =𝑘(𝑥−1)+1是表示所有过点(1,1)的直线，对吗？ ✕，因为直线方程的形式确定了斜率一定存在，因此只能表示所有斜率存在的直线 106.和X轴平行的直线的倾斜角一定是0∘，对吗？ ✓，任意直线的倾斜角范围是[0,π)，水平线倾斜角定义为0∘ 107.两条直线平行，则斜率相等，对吗？ ✕，可能两条直线的斜率都不存在。 108.两条直线垂直，则斜率之积为−1,对吗？ ✕，可能一条直线的斜率为0，另外一条直线的斜率不存在。 109.原点(0,0)到直线𝑦 =𝑘(𝑥−2)的距离最大值为2，对吗？ ✕，通过画图应该是斜率不存在的时候距离刚好是2，但此直线不可能斜率不存在。 110.点P(cosθ,sinθ)到直线x+√3y+4=0距离的最大值为3，对吗？ ✓，点P在单位圆x(cid:2870)+y(cid:2870) =1上，故只需要圆心O(0,0)到直线距离+半径即可。 (cid:2871)(cid:2976) (cid:2976) 111.一条直线的斜率为-1，则其倾斜角为 或− ，对吗？ (cid:2872) (cid:2872) (cid:2871)(cid:2976) ✕，直线的倾斜角都是[0,π)，因此不可能是负角，只能是 (cid:2872) 112.过圆内一点作圆的弦长，最长的弦为直径，最短弦和直径垂直，且该点为弦中点，对吗？ ✓，这是结论，自行证明。 113.“𝑘 =−3”是“直线𝑘𝑥−(𝑘+2)𝑦+2=0和直线𝑥−𝑘𝑦−1=0垂直”的充要条件，对吗？ - 101 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}✕，不能只看斜率之积为-1，比如k=0时直线也垂直。 114.设点P是圆(𝑥−2)(cid:2870)+(𝑦+1)(cid:2870) =4上的一个动点，则点P的坐标可以写成：(2+2cosθ,−1+2sinθ)，对 吗？ ✓，根据单位圆变换而来。即结论：圆(x−a)(cid:2870)+(y−b)(cid:2870) =r(cid:2870)上一点可以设为：(a+rcosθ,b+rsinθ)，也 叫圆的参数方程 115.过点(2,4)作圆𝑥(cid:2870)+𝑦(cid:2870) =4的切线，则切线方程为3𝑥−4𝑦+10=0，对吗？ ✕，答案不全。①若直线斜率不存在，即x=2，通过图可以知道是切线②若直线的斜率存在，设y−4= (cid:2871) k(x−2)，通过d=r解得k= (cid:2872) 116.设点𝑃(𝑥 ,𝑦 )在圆(𝑥−𝑎)(cid:2870)+(𝑦−𝑏)(cid:2870) =𝑟(cid:2870)上，则过点P作圆的切线只有一条，且切线方程为 (cid:2868) (cid:2868) (𝑥 −𝑎)(𝑥−𝑎)+(𝑦 −𝑏)(𝑦−𝑏)=𝑟(cid:2870)，对吗？ (cid:2868) (cid:2868) ✓，这是结论，可以运用点到直线距离来证明，此结论可以类比到椭圆 117.在平面直角坐标系中，恰好存在三条不同的直线同时与圆𝑥(cid:2870)+𝑦(cid:2870) =𝑚(𝑚>0)和圆(𝑥−3)(cid:2870)+ (𝑦−4)(cid:2870) =1相切，则𝑚=4，对吗？ ✕，通过圆和圆的位置关系可知：3 条公共切线→圆和圆外切，故d=r +r (此处为两个圆心之间的距离)， (cid:2869) (cid:2870) 即5=√m+1，所以m=16提醒：看清楚半径不是m 七、圆锥曲线 118.平面内到两个定点的距离之和为定值的轨迹为椭圆，对吗？ ✕.还需要满足定值大于两个定点之间的距离才是椭圆。即2a>2c 如果到两个定点的距离之和为定值且等于两个定点之间的距离，则轨迹为线段。 119.平面内到两个定点的距离之差的绝对值为定值的轨迹为双曲线，对吗？ ✕.还需要满足定值小于两个定点之间的距离才是双曲线。即2a<2c 如果到两个定点的距离之和为定值且等于两个定点之间的距离，则轨迹为两条射线。 120.椭圆(cid:3051)(cid:3118) + (cid:3052)(cid:3118) =1(𝑎 >𝑏 >0)上的点到焦点F的距离最小值为𝑎−𝑐，对吗？ (cid:3028)(cid:3118) (cid:3029)(cid:3118) ✓，如果不是焦点，那就另当别论了(感兴趣就去证明一下) 121.对于椭圆(cid:3051)(cid:3118) + (cid:3052)(cid:3118) =1(𝑎 >𝑏 >0)，若𝑎 >2𝑏，则离心率的范围是𝑒 > √(cid:2871)，对吗？ (cid:3028)(cid:3118) (cid:3029)(cid:3118) (cid:2870) ✕，离心率e= (cid:2913) =(cid:3495) (cid:2913)(cid:3118) =(cid:3495)1− (cid:2912)(cid:3118) > √(cid:2871)，范围为√(cid:2871) 0时，标准方程为(cid:2934)(cid:3118) − (cid:2935)(cid:3118) =1，即a(cid:2870) =λ,c(cid:2870) =4λ，则离心率为e= (cid:2913) =2; (cid:2971) (cid:2871)(cid:2971) (cid:2911) ②λ<0时，标准方程为(cid:2935)(cid:3118) − (cid:2934)(cid:3118) =1，即a(cid:2870) =−3λ,c(cid:2870) =−4λ，则离心率为e= (cid:2913) = (cid:2870)√(cid:2871) (cid:2879)(cid:2871)(cid:2971) (cid:2879)(cid:2971) (cid:2911) (cid:2871) 因此离心率与λ的正负有关系。(但渐近线方程与λ无关，自行证明) 126.双曲线(cid:2935)(cid:3118) − (cid:2934)(cid:3118) =1的渐近线方程为y=√3x，则离心率为2，对吗？ (cid:2911)(cid:3118) (cid:2912)(cid:3118) ✕，焦点在y轴上，y=√3x= (cid:2911) x，所以离心率e= (cid:2913) =(cid:3495) (cid:2913)(cid:3118) =(cid:3495)1+ (cid:2912)(cid:3118) = (cid:2870)√(cid:2871) (cid:2912) (cid:2911) (cid:2911)(cid:3118) (cid:2911)(cid:3118) (cid:2871) 127.设F , F 是双曲线(cid:2934)(cid:3118) −y(cid:2870) =1的左右焦点，点P(cid:3435)−4,√3(cid:3439)，则|PF |−|PF |=4，对吗？ (cid:2869) (cid:2870) (cid:2869) (cid:2870) (cid:2872) ✕，因为P在第二象限，因此|PF |<|PF |，故|PF |−|PF |=−2a=−4.务必看清楚绝对值放在哪个位置！ (cid:2869) (cid:2870) (cid:2869) (cid:2870) 128.双曲线(cid:3051)(cid:3118) − (cid:3052)(cid:3118) =1(𝑎>0,𝑏 >0)的焦点到渐近线的距离等于𝑏，双曲线 (cid:3028)(cid:3118) (cid:3029)(cid:3118) (cid:3052)(cid:3118) − (cid:3051)(cid:3118) =1(𝑎>0,𝑏 >0)的焦点到渐近线的距离也等于b，对吗？ (cid:3028)(cid:3118) (cid:3029)(cid:3118) ✓，这是结论，可以运用点到直线距离来证明 129抛物线 𝑦(cid:2870) =4𝑥 上点 𝑃 到焦点距离等于到准线距离，对吗？ ✓，这是抛物线定义的基本性质。 130.抛物线𝑦= (cid:2869) 𝑥(cid:2870)的开口向上，焦点坐标为(0,1)，对吗？ (cid:2872) ✓，化为标准方程即x(cid:2870) =4y - 103 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}131. 抛物线 𝑦(cid:2870) =4𝑥 的焦点弦长度为 (cid:2872) （𝜃 为倾斜角），对吗？ (cid:2929)(cid:2919)(cid:2924)(cid:3118)(cid:3087) ✓， 抛物线𝑦(cid:2870) =2𝑝𝑥的焦点弦长为 (cid:2870)(cid:3043) ，此处 𝑝=2，故正确。 (cid:2929)(cid:2919)(cid:2924)(cid:3118)(cid:3087) 八、概率与统计 132.现有3本完全相同的数学书和5本不一样的小说书籍，从这8本书中抽出3本，则抽到的是1本数学2 本小说抽法有30种，对吗？ ✕,3本完全相同的书中抽取1本只有一种抽法，所以答案为1×C(cid:2870) =10 (cid:2873) 133.设正整数n满足：C(cid:2870) =C(cid:2874)，则n=8，对吗？ (cid:2924) (cid:2924) ✓，组合公式的性质：C(cid:2928) =C(cid:2924)(cid:2879)(cid:2928) (cid:2924) (cid:2924) (cid:2869) (cid:2872) 134.某人做三道不同的选择题，每一道做对的概率为 ，则恰好做对一道的概率为 ，对吗？ (cid:2871) (cid:2870)(cid:2875) ✕，正确的概率计算为C(cid:2869)(cid:4672) (cid:2869) (cid:4673) (cid:2869) (cid:4672) (cid:2870) (cid:4673) (cid:2870) = (cid:2872). (cid:2871) (cid:2871) (cid:2871) (cid:2877) 135.一组数据x ,x ⋯,x 的平均数为x‾，方差为s(cid:2870)，则2x +1,2x +1,⋯,2x +1的平均数为2x‾+1，方差为4s(cid:2870)， (cid:2869) (cid:2870) (cid:2924) (cid:2869) (cid:2870) (cid:2924) 对吗？ ✓，结论：一组数据X ,X ⋯,X 的平均数为x‾，方差为s(cid:2870)，则AX +B,AX +B,⋯,AX +B的平均数为AX+B， (cid:2869) (cid:2870) (cid:2924) (cid:2869) (cid:2870) (cid:2924) 方差为A(cid:2870) s(cid:2870) 136.二项式(cid:4672)2√x− (cid:2869) (cid:4673) (cid:2874) 的展开式中，所有项的二项式系数之和为64，对吗？ (cid:2934) ✓，二项式系数之和为2𝚗，所以答案是2(cid:2874) =64 137.二项式(cid:4672)2√x− (cid:2869) (cid:4673) (cid:2874) 的展开式中，所有项系数之和为1，对吗？ (cid:2934) ✓，所有项系数之和只需要令x=1，所以答案是(2−1)(cid:2874) =1 138.设一组数据的平均数为x，方差为s(cid:2870)，在这组数据中加入一个新数据x后，则新数据的方差会比原数据的 方差要小，对吗？ ✓，因为原始数据的方差s(cid:2870) = ((cid:2908)(cid:3117)(cid:2879)(cid:2908)‾)(cid:3118)(cid:2878)((cid:2908)(cid:3118)(cid:2879)(cid:2908)‾)(cid:3118)(cid:2878)⋯(cid:2878)((cid:2908)(cid:3172)(cid:2879)(cid:2908)‾)(cid:3118) ，新数据方差为： ((cid:2934)(cid:3117)(cid:2879)(cid:2934)‾)(cid:3118)(cid:2878)((cid:2934)(cid:3118)(cid:2879)(cid:2934)‾)(cid:3118)(cid:2878)⋯(cid:2878)((cid:2934)(cid:3172)(cid:2879)(cid:2934)‾)(cid:3118)(cid:2878)((cid:2934)‾(cid:2879)(cid:2934)‾)(cid:3118) ，分 (cid:2924) (cid:2924)(cid:2878)(cid:2869) 子不变，分母变大，故方差变小了。 139.若随机变量X~N(2,σ²)，则P(X>2.5)=0.5-P(22)=0.5，再减去P(21），可以选取数字1进行代入检验。若1符合题意，则排 除B；若1不符合题意，则排除A。这种方法能迅速缩小选择范围，但需注意，选取的数值应考虑选项特征， 避免选择所有选项共有或均不包含的数值。此外，还可以根据选项涉及的知识点进行论证排除。例如，若 四个选项分别对应四个知识点，可以优先对熟悉的知识点进行验证，判断其是否符合题意，从而快速准确 地锁定正确答案，避免因知识点掌握不牢固或理解模糊而导致误选。 而历年高考的选择题都采用的是“四选一”型，即选择项中只有一个是正确的，所以排除法是快速解决部 分高考选择试题从而节省时间的有效方法。那对于填空题呢，其实也是可以的，比如有些填空题如果你已 经求出了结果，但并不确定这个结果中的某个端点值是否要取，你就可以代入验证进行排除。所以，我们 要熟练掌握这种能帮助你快速找到正确结论的方法，从而提高解题效率，为后面的试题解答留有更充足的 时间！ （3）特例法 特例法对解决有关数学题目是一种非常独特且十分有效的方法，它可以使繁杂的问题处理简易化，收 到事半功倍的效果。 特例法，即特殊值验证法，可通过特殊数值、图形、位置替代普遍条件，导出特殊结论，进而检验选 项，做出正确选择。尤其针对棘手的高考选择题或填空题，关注特殊情况，从特殊角度入手，常能迅速简 捷解题。 常用特例包括特殊数值、点、数列、函数、图形、角、位置等。特例法是解答选择题的最佳方法之一， 具体是通过特例的方式提高解题速度，题中的一般情况必须满足我们取值的特殊情况，从而我们选取适当 的特值帮助我们得到正确的结论。比如，某个数列，可以考虑等差数列或等比数列的情形；某个三角形， 可以考虑直角三角形或等边三角形；椭圆上某点，可以考虑长轴或短轴的端点等，但前提是所取特例需符 合题目所有条件。 - 112 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}特例法能简化运算和推理过程，尤其适用于包含字母或一般性结论的选择题和填空题，但在应用时需 注意以下几点：（1）取特例尽可能简单，有利于计算和推理；（2）若在不同的特殊情况下有两个或两个 以上的结论相符，则应选择另一特例情况再检验，或改用其他方法求解；（3）若正确选项在题目的普遍条 件下均成立，则应选取最简单的特殊值进行探究，以此快速、准确地得出答案。这种方法，即通过对特殊 情况的考察来推断一般规律，是解答此类选择、填空题的优选策略。 近年来高考选择、填空题中可用或结合用特例法解答的试题能占到 30%左右，所以要想快速准确地赢 得时间获取高分，一定要学会、会用并且灵活使用特例法！ （4）估算法 估算法，包括四舍五入法、估算范围法、数值特点估计法以及接近整十、整百、整千的估算等，是解 决数学问题的快速方法，它不仅能够提高解题速度，还能帮助考生避免在计算过程中出现大的失误。 对于高考数学某些问题，当我们没有合适的解题思路或正面解析比较麻烦，特别是针对选择题时，不 必进行准确的计算，我们可以通过适当地放大或缩小部分数据估算出答案的大概范围或者近似值，也可以 通过对其数值特点和取值界限作出适当的估计，便能作出正确的判断，这就是估算法。 当然，这有时也适合用在填空题中，比如比较大小时。估算法不仅能有效减少运算量，还能提升思维 的深度与层次，因此，我们应熟练掌握并灵活运用这一技巧。 而对于选择题，实在没思路时，又不需要解题过程，我们用这种方法还是能很大程度上提高我们的得 分率的，比如，求某个图形的面积或体积，当选项差距比较大时，我们只需通过计算一部分比较好计算或 自己熟练掌握的，就可以通过比较各选项得出正确结论。 （5）数形结合法 数形结合法，也就是我们常说的图解法，就是把抽象的数学语言、数量关系与直观的几何图形、位置 关系结合起来，通过“以形助数”或“以数解形”，即通过抽象思维与形象思维的结合，可以使复杂问题简单化， 抽象问题具体化，从而实现优化解题途径的目的。 在高考中，数形结合是一种常用的解题方法，也是一种重要的数学思想方法，特别是在一些计算过程 复杂的函数、三角、解析几何等问题中，可以先作出有关函数的图像或者构造适当的几何图形，再利用图 示辅助，即参照图形的做法、形状、位置、性质，综合图像的特征进行直观分析，从而得出结论。比如： ①在集合运算中常常借助于数轴、Venn 图来处理集合的交、并、补等运算，从而使问题得以简化，使 运算快捷明了。 ②借助于图象研究函数的性质是一种常用的方法。函数图象的几何特征与数量特征紧密结合，体现了数形 结合的特征与方法。 ③处理方程问题时，把方程的根的问题看作两个函数图象的交点问题；处理不等式时，从题目的条件 与结论出发，联系相关函数，着重分析其几何意义，从图形上找出解题的思路。 ④有关三角函数单调区间的确定或比较三角函数值的大小等问题，一般借助于单位圆或三角函数图像 来处理，数形结合思想是处理三角函数问题的重要方法。 ⑤数列是一种特殊的函数，数列的通项公式以及前 n 项和公式可以看作关于正整数 n 的函数。用数形 - 113 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}结合的思想研究数列问题是借助函数的图像进行直观分析，从而把数列的有关问题转化为函数的有关问题 来解决。 ⑥解析几何的基本思想就是数形结合，在解题中善于将数形结合的数学思想运用于对点、线、曲线的 性质及其相互关系的研究中。 ⑦立体几何中用坐标的方法将几何中的点、线、面的性质及其相互关系进行研究，可将抽象的几何问 题转化为纯粹的代数运算。 著名数学家华罗庚曾说过：“数形结合百般好，隔离分家万事休。”数形结合是数学解题中的一把利剑， 它能让抽象的数学问题变得直观且生动，将抽象思维转化为形象思维，从而帮助我们更深刻地理解数学问 题的本质。另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷。所以，我们一定要学 好并应用好数形结合的方法。 三、解题思想方法 1.函数或方程或不等式的题目，先直接思考后建立三者的联系。首先考虑定义域，其次使用“三合一定理”； 2.如果在方程或是不等式中出现超越式，优先选择数形结合的思想方法； 3.对于含有参数的初等函数，研究时应聚焦于参数未改变的那些恒定性质，例如函数所经过的固定点、 二次函数的对称轴等。 4.选择题与填空题中出现不等式的题目时，优选特殊值法； 5.求参数的取值范围时，应该建立关于参数的等式或是不等式，用函数的定义域或是值域或是解不等式 完成，在对方程或不等式进行变形处理时，优先考虑使用分离参数的方法来简化问题。 6.恒成立问题或是它的反面，可以转化为最值问题，注意二次函数的应用，灵活使用闭区间上的最值， 分类讨论的思想，分类讨论应该不重复不遗漏； 7.在解答圆锥曲线的题目时，应优先考虑利用它们的定义来求解。对于直线与圆锥曲线的相交问题，如 果涉及到弦的中点，可以选择设而不求的点差法；如果与弦的中点无关，则可以选择利用根与系数的关系 公式法。在使用根与系数的关系公式时，务必先判断是否为二次方程，并考虑根的判别式。 8.在求解曲线方程的题目时，若已知曲线的形状，可采用待定系数法；若未知曲线的形状，则需按照建 系、设点、列式、化简的步骤进行求解，同时要注意去掉不符合条件的特殊点。 9.要求解椭圆或双曲线的离心率，只需建立关于a、b、c之间的等式关系即可得出答案。 10. 求三角函数的周期、单调区间或是最值，优先考虑化为一次同角弦函数，然后使用辅助角公式解答； 解三角形的题目，重视内角和定理的使用；与向量联系的题目，注意向量角的范围； 11.数列的题目与和有关，优选作差的方法；注意归纳、猜想之后证明；猜想的方向是两种特殊数列； 解答的时候注意使用通项公式及前n项和公式，体会方程的思想； 12.立体几何第一问若旨在辅助建系，则应采用传统方法解答；若非如此，可从第一问起即建立坐标系 求解。需特别注意，向量角与线线角、线面角、面面角各不相同，应熟练掌握这些角度间三角函数值的转 换方法。计算锥体体积时需注意相关系数，计算三角形面积时亦需关注其系数。涉及球的题目同样需谨慎 对待，可通过连接“心心距”构造直角三角形来解题。 - 114 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}13.导数的常规题目一般不难，但要注意解题的层次与步骤，如果要用构造函数证明不等式，可从已知 或者前一问中找到突破口，必要时应该放弃；重视几何意义的应用，注意点是否在曲线上； 14.概率与统计的解答题，应该先设事件，然后写出使用公式的理由，当然要注意步骤的多少决定解答 的详略；若存在分布列，则验证其概率和是否为1是检验答案正确性的关键步骤。 15.遇到复杂的式子可以用换元法，使用换元法必须注意新元的取值范围，若式子为勾股定理型的，可 使用三角换元来完成； 16.注意概率分布中的二项分布，二项式定理中的通项公式的使用与赋值的方法，排列组合中的枚举法， 全称与特称命题的否定写法，取值范围或是不等式的解的端点能否取到需单独验证，用点斜式或斜截式方 程的时候考虑斜率是否存在等； 四、每分必争 1.答题时间共120分钟，而你要答分数为150分的考卷，算一算就知道，每分钟应该解答1分多的题目， 所以每 1 分钟的时间都是重要的。试卷到手后，首先进行必要的检查，确认无印刷模糊之处，并完成填涂 工作。随后，立即浏览试卷，熟悉可能用到的公式，做到胸有成竹。对于简单的题目，要用心计算，必要 时动笔也无妨（无论是写名字还是字母，无人会细究）。 2.在分数上也是每分必争。正如参考资料所述，成绩合格率反映了达到基本要求的比例。因此，你得到 89分与得到90分，虽然只差1分，但意义截然不同：一个是不合格，一个是合格。虽然高考中仅差1分， 例如 509 分与 510 分，这可能在某些情况下影响录取结果，如接近录取分数线时，分数稍高者可能更易被 录取。然而，高考成绩并非唯一评判标准，综合素质评价和面试成绩等其他因素也会影响录取。因此，1分 之差虽然重要，但个人的综合素质和潜力同样关键。所以，在答卷的时候要精益求精。 对单选题的每一个选项进行评估，看与你选的相似的那个是不是更准确？ 多选题找到两个必选项了没？ 填空题的范围书写是不是集合形式，是不是少或多了一个端点？是不是有一个解应该舍去而没舍？ 解答题的步骤是不是按照公式、代数、结果的格式完成的，应用题是不是设、列、画（线性规划）、 解、答？根据已知条件你还能联想到什么？把它写在考卷上，也许它就是你需要的关键的 1 分，为什么不 去做呢？ 3.面对答题时间的紧迫感，是所有学生共同的体验。若要缓解这种压力，唯一的方法便是学会取舍，准 确判断并放弃那些不必要的部分，从而为争取每一分创造条件。 4.稍作冷静，虽然表面上看似浪费了时间，但实际上却是在为自己争取机会，甚至可能因此创造出意想 不到的奇迹。在头脑混乱的时候，不妨停下来，喝口水，深吸一口气，再慢慢呼出，就在呼出的同时，你 就会得到灵感。 5.如果题目分析遇到困难，很可能是因为忽略了某个重要的已知条件，因此，需要重新审题，仔细阅读 题目，才能有所发现，切勿局限于固定的思维模式。联想你做过的类似的题目的解题方法，把不熟悉的转 化为你熟悉的也许就是成功。 6.高考只是人生众多重要考试中的一场，而人生则是由无数个一分钟组成的。只有珍惜并把握好每一分 - 115 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}钟，才能真正掌控自己的人生。高考不过是一场平常的模拟考试，真正的高考其实是在我们生活的每一刻。 3.高考数学临场解题策略 高考的特点是以学生解题能力的高低为标准的一次性选拔，这就使得临场发挥显得尤为重要，研究和 总结临场解题策略，进行应试训练和心理辅导，已成为高考数学的重要内容之一，正确运用数学高考临场 解题策略，不仅可以预防各种心理障碍造成的不合理丢分和计算失误及笔误，而且能运用科学的检索方法， 建立神经联系，挖掘思维和知识的潜能，考出最佳成绩。 一、调整大脑思绪，提前进入数学情境 考前要摒弃杂念，排除干扰思绪，使大脑处于“空白”状态，创设数学情境，进而酝酿数学思维，提前进 入“角色”， 通过清点用具、暗示重要知识和方法、提醒常见解题误区和自己易出现的错误等，进行针对性的自我 安慰，从而稳定情绪、增强信心，减轻压力、轻装上阵，使思维单一化、数学化，以平稳自信、积极主动 的心态准备应考。 二、“内紧外松”，集中注意力，消除焦虑怯场 集中注意力是考试成功的保证，一定的神经亢奋和紧张，能加速神经联系，有益于积极思维，要使注 意力高度集中，思维异常积极，这叫内紧，但紧张程度过重，则会走向反面，形成怯场，产生焦虑，抑制 思维，所以又要清醒愉快，放得开，这叫外松。 三、沉着应战，确保旗开得胜，以振奋精神 良好的开端是成功的一半，从考试的心理角度来说，这确实是很有道理的，拿到试题后，不要急于求成、 立即下手解题，而应通览一遍整套试题，摸透题情，然后稳操一两个易题熟题，让自己产生“旗开得胜”的快 意，从而有一个良好的开端，以振奋精神，鼓舞信心，很快进入最佳思维状态，即发挥心理学所谓的“门坎 效应”，之后做一题得一题，不断产生正激励，稳拿中低，见机攀高。 四、“六先六后”，因人因卷制宜 在通览全卷，将简单题顺手完成的情况下，情绪趋于稳定，情境趋于单一，大脑趋于亢奋，思维趋于 积极，之后便是发挥临场解题能力的黄金时间了。这时，考生可依自己的解题习惯和基本功，结合整套试 题结构，选择执行“六先六后”的战术原则。 1.先易后难。即先做简单题，再做综合题。应根据自己的实际情况，果断跳过“啃”不动的题目，从易到 难，也要注意认真对待每一道题，力求有效，不能走马观花，有难就退，伤害解题情绪。 2.先熟后生。通览全卷，可以得到许多有利的积极因素，也会看到一些不利之处。对后者，不要惊慌失 措，应想到试题偏难对所有考生也难，通过这种暗示，确保情绪稳定。对全卷整体把握之后，就可实施先 熟后生的策略，即先做那些内容掌握比较透彻、题型结构比较熟悉、解题思路比较清晰的题目。这样，在 拿下熟题的同时，可以使思维流畅、超常发挥，达到拿下中、高档题目的目的。 3.先同后异。即先做同科同类型的题目，思考比较集中，知识和方法的沟通比较容易，有利于提高单位 时间的效益。高考题一般要求较快地进行“兴奋灶”的转移，而“先同后异”，可以避免“兴奋灶”过急、过频的 - 116 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}跳跃，从而减轻大脑负担，保持有效精力。 4.先小后大。小题一般是信息量少、运算量小，易于把握，不要轻易放过，应争取在解答大题之前尽快 解决，从而为解决大题赢得时间，创造一个宽松的心理基础。 5.先点后面。近年的高考数学解答题多呈现为多问渐难式的“梯度题”，解答时不必一气审到底，应走一 步解决一步，而前面问题的解决又为后面问题准备了思维基础和解题条件，所以要步步为营，由点到面。 6.先高后低。即在考试的后半段时间，要注重时间效益，如估计两题都会做，则先做高分题;估计两题 都不易，则先就高分题实施“分段得分”，以增加在时间不足前提下的得分。 五、一“慢”一“快”，相得益彰 有些考生只知道考场上一味地要快，结果题意未清，条件未全，便急于解答，岂不知欲速则不达，结果是 思维受阻或进入死胡同，导致失败。应该说，审题要慢，解答要快。审题是整个解题过程的“基础工程”，题 目本身是“怎样解题”的信息源，必须充分搞清题意，综合所有条件，提炼全部线索，形成整体认识，为形成 解题思路提供全面可靠的依据。而思路一旦形成，则可尽量快速完成。 六、确保运算准确，立足一次成功 数学高考需要在120分钟时间内完成22道题，时间很紧张，不允许做大量细致的解后检验，所以要尽 量准确运算(关键步骤，力求准确，宁慢勿快)，立足一次成功。解题速度是建立在解题准确度基础上的，更 何况数学题的中间数据常常不但从“数量”上，而且从“性质”上影响着后继各步的解答。所以，在以快为上的 前提下，要稳扎稳打，层层有据，步步准确，不能为追求速度而丢掉准确度，甚至丢掉重要的得分步骤。 假如速度与准确不可兼得的话，就只好舍快求对了，因为解答不对，再快也毫无意义。 七、讲求规范书写，力争既对又全 考试的又一个特点是以卷面为唯一依据。这就要求不但会而且要对，对且全，全而规范。会而不对，令 人惋惜;对而不全，得分不高;表述不规范、字迹不工整又是造成高考数学试卷非智力因素失分的一大方面。因为 字迹潦草，会使阅卷老师的第一印象不良，进而使阅卷老师认为考生学习不认真、基本功不过硬、“感情分”也就 相应低了，此所谓心理学上的“光环效应”。“书写要工整，卷面能得分”讲的也正是这个道理。 八、面对难题，讲究策略，争取得分 会做的题目当然要力求做对、做全、得满分，而更多的问题是对不能全面完成的题目如何分段得分， 下面有两种常用方法： 1.缺步解答。对一个疑难问题，确实啃不动时，一个明智的解题策略是：将它划分为一个个子问题或一 系列的步骤，先解决问题的一部分， 即能解决到什么程度就解决到什么程度，能演算几步就写几步，每进行一步就可得到这一步的分数。如从 最初的把文字语言译成符号语言，把条件和目标译成数学表达式，设应用题的未知数，设轨迹题的动点坐 标，依题意正确画出图形等，都能得分。还有像完成数学归纳法的第一步，分类讨论，反证法的简单情形 等，都能得分。而且可望在上述处理中，从感性到理性，从特殊到一般，从局部到整体，产生顿悟，形成 思路，获得解题成功。 - 117 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}2.跳步解答。当解题过程卡在一中间环节上时，可以承认中间结论，往下推，看能否得到正确结论，如 得不出，说明此途径不对，立即改变方向，寻找其他途径;如能得到预期结论，就再回头集中力量攻克这一 过渡环节。若因时间限制，中间结论来不及得到证实，就只好跳过这一步，写出后继各步，一直做到底;另 外，若题目有两问，第一问做不上，可以第一问为“已知”，完成第二问，这都叫跳步解答。也许后来由于解 题的正迁移对中间步骤想起来了，或在时间允许的情况下，经努力而攻下了中间难点，可在相应题尾补上。 九、考前寄语 ①难易分明，决不耗时； ②慎于审题，决不懊悔； ③必求规范，决不失分； ④细心运算，决不犯错； ⑤提防陷阱，决不上当； ⑥愿慢求对，决不快错； ⑦遇新不慌，决不急躁； ⑧奋力拼杀，决不落伍. - 118 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}- 119 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}4.新高考数学多项选择题的解题策略与技巧 新高考改革取消文理科，对统考科目设新要求。2020 年山东、海南采用新课程标准，依 据《新课标考试纲要》命制试题。2022 年，广西也开始实行新高考改革，2024年是新高考改 革的第一年高考，试题中多出多选题题型，考查容量大、知识面宽，解题思路广，数学思想丰 富。本文通过对近年高考多项选择题进行研究，把握多选题命题特点，对多项选择题的解题方 法进行了反思，掌握解答技巧。 一、多选题的考查性质和特点 多选题作为新高考改革中的一种重要题型，充分体现了对“四基”“四能”及核心素养的考查。 这种题型主要侧重于学生的基础知识和基本技能的测试，通过合适的试题情境和相应的题目背 景，能够实现对同一情境下多个结论的判断和选择。多选题并不是简单地将知识点拼凑在一起 进行考查，而是更加注重考查学生在知识储备和技能掌握方面的综合运用能力。其主要特点表 现为：题目设计灵活多样，能够有效地测试学生的思维能力、分析能力、判断能力和综合运用 知识的能力；同时，多选题还能够引导学生更加注重知识之间的联系和贯通，从而提高学生的 综合素质和未来发展潜力。 （1）无需解题过程 多选题与单选题类似，都要求学生从提供的选项中选择正确答案。不同之处在于，多选题 需要学生选择多个正确答案，而不是仅选择一个。同样，多选题也不需要学生具体书写解题过 程，只要选择出正确的答案，就能得到相应的分数。 （2）分值灵活 新高考的选择题由 8 个单选题和 4 个多选题组成，每题 5 分，共计 60 分。在多选题中， 考生需全选对才能获得5分的满分，若只选对部分答案，只获得2分的得分，而如果考生有选 错或未选的选项，该题将被判为0分。今年九省联考多选题的付分方式也有所改变，多选题为 3 题，每题 6 分，共计 18 分；考生全选对获得 6 分的满分，如果正确选项是两个的话，选一 个正确的3分，全对，得6分；如果正确选项是3个的话，选一个正确的2分，选两个且正确 的4分。 （3）考查知识内容多样化 新高考中的多选题涉及多个知识点，需要考生具备较为全面的数学素养。在解答多选题时， 学生需要排除并验证每个选项的正确性，这不仅增加了对知识点的考查，同时对考生的能力也 提出了更高的要求，从而提高了试题的难度。 - 120 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}（4）考查策略需选择 多选题允许学生利用已选答案作为已知条件进行推断，从而减少对每个选项的重复计算。 这种解题思路的多样性和灵活性可以节省学生的时间，提高解题效率。 （5）考查创新思维 多选题鼓励学生运用创新思维和创造性解决问题的能力，题目可以是新的，也可以是旧的， 但是解决问题的方法和思路需要有创新性。多个选项的数学问题可以涵盖多种不同的数学思想 方法，这对学生的思维方式与能力提升均有显著的助益。 （6）能更好地区分学生的能力层次 多选题不仅测试学生对数学知识的掌握程度，同时亦对其综合素质进行考察，这些素质包 括时间管控、心理素质以及应变能力等。多选题采用的多级得分模式对提高低水平学生的得分 具有积极作用，同时也有助于区分出高水平的考生。因此，这种方法能够更为精准地评估不同 能力层次的考生，从而有助于选拔优秀人才。 二、数学多选题的基本类型 数学多项选择题的设计方案，根据其选择支的差异化特性，可以大致划分以下六种基本类 型： 1. 条件缺失型：此类题目是一种常见的数学问题类型，其特点是在生成干扰选项时会故 意省略某些易于遗漏的条件。这种题型旨在测试学生的细心程度和考虑问题的全面性。在解决 这类问题时，学生需要仔细审题，并尽可能将所有已知条件和限定条件都考虑到。否则，如果 忽略了某个重要条件，就可能会得出错误的答案。因此，在面对条件缺失型题目时，学生需要 保持高度警觉，并对每个条件进行认真分析和推理。 2. 实际背景忽视型：这种类型题目是一种非常具有挑战性的题目类型，它通过仔细地模 拟学生在计算过程中可能出现的错误和失误，构造出具有较强迷惑性的干扰选项。这种类型的 题目在提升试题的针对性和区分度方面具有显著的效果，因为它能够有效地测试学生对于基本 计算技能的掌握程度，同时也能检测学生对于题目背后实际应用背景的理解程度。在模拟这种 题目时，需要注意细节和精度，确保干扰选项的构造符合实际情况，并具有一定的迷惑性。这 样才能使题目更加具有挑战性和区分度，从而有效地测试学生的实际水平。 3. 概念混淆型：此题型是一种常见的数学测试题型，旨在考查学生对于数学相关概念、 性质的理解和掌握程度。这种类型的题目通常会设计一些干扰选项，以混淆学生的判断，让学 生在进行选择时容易产生困惑和犹豫。在设计概念混淆型题目时，出题者通常会选择一些学生 容易混淆的概念或者性质作为考点，例如相似三角形和全等三角形、函数和方程等等。 - 121 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}4. 题意误解型：这种题目是一种常见的干扰选项，通常是由于考生在考试过程中读题不 严谨、审题不细致，导致对题目要求和意图产生误解，从而得出了错误的结论而设计的。这种 干扰选项通常会利用考生对题目中某些关键词汇或细节的理解不足，或者利用考生对题目背景 和知识点的掌握不全面等漏洞进行设计。 5. 推理错误型：这种类型题目是一种常见的逻辑推理题目，其特点在于题目中给出了不 完整或不合逻辑的推理过程，而干扰选项则通常是由这个不正确的推理过程所产生的不正确结 果。在解决这类题目时，需要考生认真阅读题目，理解推理过程，并从中找出推理错误，从而 排除干扰选项，找到正确答案。常见的推理错误包括：偷换概念、前提不足、因果倒置、非黑 即白等。 6. 思维定势型：这种类型题目是一种较为常见的题目类型，通常会以某种形式隐藏在看 似熟悉的条件和相似的形式中。这些题目通常会利用人们习惯性的思维方式，通过巧妙地伪装 和误导性的信息，来引发错误的类比和联想。在这种类型题目中，干扰选项往往是设计来诱使 答题者陷入思维定势，从而忽略题目中的关键细节或隐含条件。对于这种题目，关键是要保持 清醒的头脑，仔细阅读题目并审慎分析，以便突破思维定势的束缚，找到正确的答案。 三、多选题解题方法与技巧 多选题通常要求考生从四个选项中选择两个或以上正确答案，但所有选项都正确的极少出 现。这类题目考查知识面广，要求考生对数学基础有深刻理解并全面掌握。考生面对多选题需 熟悉并掌握几种解题策略，因为从四个选项中选一个答案转变为选多个答案，更具挑战性。 2.1求解对照法（直接法） 这种方法为同学们所熟知，解题时，首先要完整读取题目信息，既需阅读题干，亦需阅读 四个选项。对关键的字眼应予以仔细辨识，以免出现误解或遗漏，从而造成不必要的失分。在 理解题目条件的基础上，应迅速联想到相关的概念、公式、定理以及常见的思想方法。同时， 还需找出题目中的隐含条件，深入理解题目的真实含义。由于高考的题量较大，若所有选择题 均采用直接求解对照法（即直接法）进行解答，时间上将无法充分保障，甚至有些题目在短时 间内可能无法得以妥善解决。因此，我们需要掌握并运用其他的方法进行解题。 2.2特值检验法 根据题干或选项的要求，为变量赋予特定值，是帮助选择正确答案的有力手段。此外，这 种方法亦可用来识别错误答案。特别是针对多选题，答案往往含有多个正确选项，此时考生可 通过预先设定特殊值，将其代入选项中进行检验。若某些选项与预设值不符，则可直接排除， 从而缩小了答题的范围，有效节约了解题时间。 - 122 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}2.3逆推代入法 将选项中给出的答案，代入题干逐一去验证是否满足题设条件，用时注意，考虑全面，避 免遗漏。如求取值范围的问题可用这种方法，不但能节省繁杂的计算过程，而且可争取到更多 的考试时间。 2.4排除法 排除法指的是可以通过排除错误选项，节省推导和计算时间.在多项选择题中，尤其是当 你确定其中两个选项为错误时，则另外两个肯定是正确选项（至少存在两个正确选项）。经过 对近年高考试题进行深入分析和研究，我们发现一个较为显著的模式：在四道多选题中，至少 有两道的正确选项数量仅为两个。 2.5逻辑分析法 逻辑解析法：该方法通过剖析四个选项之间的逻辑联系，以否定错误选项，从而挑选出正 确选项。举个例子，在多选题中，如存在两对内容互相对立的选项，我们应从两对对立选项中 各自挑选一个选项作为正确答案。比如在ABCD四个待选答案中，AB和CD 两组选项互相对 立。此时，我们应从AB和CD 两组中各选择一个答案。另外，如果存在两对内容相近或相似 的选项，且这两对选项内容对立，那么其中一对相近或相似的选项应该是正确答案。比如在 ABCD四个待选答案中，AB和CD 的内容相近且对立。如果判断A项正确，则AB两组都正 确；如果判断C 项正确，则CD 两组都正确。 2.6宁缺毋滥法 也称为“逃避策略”，源于中国古代兵法的三十六计“走为上”，是在有充分把握时的首选策 略。有把握的选项应当被毫不犹豫地选择；而对于没有把握的选项，应坚决地放弃。猜对的概 率最高仅为50%，若不幸猜错，本题将被判定为0分。在面对多项选择题时，应明确强烈的审 慎原则，首先选出2个最有信心的选项，只有在确信还有其他正确选项时，才能继续筛选。否 则，拒绝选择，以防止错误答案的出现。这样，才能保障基本得分。因此，在处理选项时，我 们应坚持宁缺毋滥，这与单项选择题的处理方式存在显著差异。 总之，新高考中数学多项选择题的引入与设置，为数学知识的教学与考查提供了更多的平 台，同时也为不同水平的学生提供了更多得分的机会，更加准确地评估和区分了学生不同层次 的数学基础和能力水平。此外，不同类型的数学多项选择题和相应的解题策略也相继出现，这 些策略在应用时并不是孤立的，而是相互交织和融合的。因此，学生在解题时需要综合考虑， 并巧妙地运用这些策略。教师在教学过程中应着重巩固基础，注重概念讲解，平日教学中要灌 输学生数形结合、分类讨论等解题方法。 - 123 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}- 124 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}5.高考数学阅卷和答题卡确注意事项 一、扫描 1.如果不使用规定的2B铅笔，可能识别被误判为“空选”，造成失分。 2.答题要规范，否则若无法辨认，容易误判或不给分。 3.作图未使用规定铅笔，或下笔太轻，会造成扫描看不清楚，请慎重。 - 125 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}4.语言表述需简明扼要，勿超出答题区域。 二、阅卷 1.主观题和客观题 一般客观题为选择题，由电脑自动阅卷完成；主观题为填空题、解答题，划分区域后，由人工网上阅 卷完成。改卷中存在争议的部分，往往都是主观题部分。 2.正评和仲裁 每次考试，一般每道题由两位老师独立评分，即为正评。评卷前会在系统内设定一个允许误差，一般 是 2 分，若两位老师评分不超过允许误差，则得分按均值计算；若评分超过允许误差，则试卷提交到第三 位老师进行仲裁，作为最终结果。 3.评卷误差的产生 评卷误差的产生，主要有两个原因：一是解题过程的规范性，二是书写的规范性。 由于解题过程的不规范，其实是方法掌握得不够全面，各题迥异不具代表性，这里主要展示一些书写 规范性的问题。 ①潦草的字迹，无法辨认，或容易引起歧义。 ②解答题未化简到最终结果可能会多扣分; - 126 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}③填空题以下情况全扣; ④千万别和阅卷老师开玩笑，情节严重者，本题即使有部分正确依然0分处理。 建议同学们要注意平时作业和考试中的书写，一定要非常规范，养成良好的习惯，这样在高考中就会 很自然地书写规范，考出自己满意的成绩！ 三、阅卷教师希望看到的是能够减轻阅读量的卷面，具体包括以下6点： 1.卷面清洁，这是最基本的要求； 2.书写工整，字迹清晰； 3.在规定的答题区域答题，否则做无用功； 4.表述是要根据分值思考要点，尽量细分，用分号或①②③④等符号清楚表述； 5.语言要简洁，答中要害； 6.语言表述要规范，尽量用专业术语。 如果卷面做到了以上6点，在“可给分可不给分的情况时，从宽给分”的高考评分原则下，将无形中增加 了多得分的砝码。 - 127 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}四、以下是网上阅卷中发现的考生答题不规范的典型情况： 1.字迹潦草 问题一：字迹潦草、字迹过淡的情况不少。高考阅卷是在计算机中阅读扫描后的考生答题卡，没有平 时纸质阅卷那么清晰易认，加上高考阅卷时间短、任务重，因此字迹不清楚的试卷是不受阅卷老师欢迎的。 【应对】书写差的学生应加强书法练习，不仅每个字要力争书写工整、大方，而且整个卷面要做到干净、 清洁；答题卡答题范围设置是假定用三号字书写两倍正确答案字数的大小，考生无需担心字写大了书写空 间不够；考试时统一要求学生使用配套的0.5mm考试专用水芯笔，避免笔迹过淡或过浓导致扫描不清晰。 2.题号填涂与作答不符 问题二：试卷中有选考题，要求考生除了答出所选题目的答案外，还要在答题卡中将相应的选择题号 涂黑，而部分考生出现答题内容与所涂题号不一致的情况，这样做，该题 0 分。例如，考生涂的是 9 题题 号，答的却是10题的内容，只能得零分。 【应对】答选考题时，一定要头脑清醒，选定要答的题目一定要涂 对题号，否则白费了工夫，还不得分。 3.超出规定区域答题 问题三：部分学生还没想好便匆忙答题，以至于格式没安排好，超 出了该题预留的答题位置。在网上阅卷中，超出规定区域的答案无效。 【应对】答大题时，想好了再动笔，先答什么，后答什么，要有条理，不能写了半天还没入主题，重 要的东西没地方写了，再东找点地方，西找点地方写，结果不得分。 4.答案分块 问题四：有的学生答案布局不合理，内容分成了几块。“分块”现象容易导致阅卷老师漏阅得分点，造成 赋分过少的现象。 【应对】高考试题中的非选择题一般是一个要点 2 分。因此，书写答案前先确定需要书写的要点个数， 规划好答案的整体布局，在书写前对答案打好草稿，然后从左上角往右下角书写，这样就不会出现图示的“分 块”现象；备考过程中加强对高考非选择题答案的揣摩，分析答案要点有几个，答案依据在哪，为什么只答 这几个要点等。做到答题时条理分明，避免书写之后又补充答案的现象。 5.答案不分层次 问题五：不少考生答一道大题时，没有层次，一口气写了一大段，让阅卷老师很难查找知识点。 【应对】对于一道需要答出很多采分点的大题，考生作答时要尽可能做到有层次，这样能让阅卷老师 感觉到该考生思路是清晰的，便于得高分。 6.作图不规范 问题六：部分学生在答题卡上作图不清晰，要不过淡，要不就东一条线、西一条线，擦又没擦干净，显得 很脏，这让阅卷老师很难辨识清楚。 【应对】作图题要本着清晰、干净的原则，该用尺子的地方一定要用尺子，线条要重些，但又不能让 其看起来显得很脏。 7.出现删除符号 问题七：部分考生匆忙答题，答错了一段，便用删除符号大面积删掉。 【应对】很多学生感觉答题出现错误时，往往使用删除符号划掉部分字词，这是一个极其错误的思维定 势。 高考阅卷有一个“采点得分”原则，即只看对的答案。只要不是同一句话中前后矛盾，那么即使是错误的 答案也不会影响考生应得分数。因此，在不允许“打补丁”的前提下，已经书写的答案就不要使用删除符号。 解决方案：1.如果答案中已经用数字标注①、②、③等，则无需进行修改。2.如果没有使用数字标注的 习惯，则在认为要删除的答案前后标上句号，使其与别的答案存在并列关系。 五、数学阅卷中给考生在考试中发挥提几点意见： 1.发挥最大潜能，让考分达到最大值，忽略其他一切与考试无关的东西。 2.立体几何第1问一般较为简单，用一般知识即可解决，不必用空间向量求解，但第2问一般都要建坐 标系用向量求解。 3.由于每道大题答题框面积有限，故答题只能写必要关键步骤，有些课本上没有的常规结论直接使用。 4.如果将前面的过程写得过细，必然会导致后面拥挤，关键的内容没有写上。 5.大家知道，大题不能留空白，“会而不对”的题将涉及的知识套上去，必要时用“瑕疵”法求解。 6.大胆使用归纳、类比，赋值法。 7.熟知高考数学解答题的评分标准：解答题评分的大思想“踩点给分”，先由评卷全体老师把该题可能有 - 128 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}的解法都解出来，每种解法，细化步骤，讨论哪一步给多少分，直到评卷组长通过为止。 6.解答题解题模型 - 129 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}概率条统计 - 130 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}- 131 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}考前注意篇 1.考前考生需要做哪些准备 一年一度的高考即将来临，又是千千万万学子寒窗苦读12年，怀揣大学梦，共挤独木桥的夏季，在离 高考只剩下半个月的时间，高三的学生们该如何做好高考前的准备呢？这里不仅有文化课的准备，还有心 态的准备，需要做到劳逸结合，保持好心态，保持好身体，高考才能正常发挥。现在就为正在努力备考的 学生们分享一下高考前的准备工作。 知识准备 1.不做题海战术。距离高考时间越来越近，这时不能够再把时间花在题海战术上，可能有些同学说，如 果不保持每天的做题量，锻炼自己的做题速度跟准确度，很难保证在考场上有正常的发挥。其实，我们应 该把更多的时间分配到各科的基础复习当中，然后在每天复习完之后，适当选择一些题目出来练习，建议 按照规定的时间完成每一道题目，也能达到考场中的那种紧张感。 2.注重课本基础知识点的复习。这时已经不是做难题做偏题的时候，在这么短的时间，想要有一个突破 - 132 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}性的提高，基本已经很难，同学们应该把更多的精力放在课本基础知识点的掌握与复习当中，高考面向的 是所有学生，试题大部分偏向于基础，而少部分的难题作为中高层学生的拉分机会。当然，题目难，得分 也难；题目易，失分也容易，考场更需要胆大心细，做到易题不丢分，难题争得分。 3.分析自己的优势弱势环节。复习时，要客观理清自己的优势科目、弱势科目。如果理科是弱势，那么 这时再强化做题基本已经来不及了，反而应该多看看课本上的基础性原理跟公式的应用，保证基础题目能 够得分，而且是尽量拿满分，减少失误；如果弱势在于文科，那么在接下来的时间里面，还有机会进行一 小段的提高，比如可以多花一些时间背诵名人警句，多看看优秀作文，多背背英语单词，听一听听力，培 养自己的语感，一直持续到高考该科目的结束，相信会有一个不错的效果。 4.翻阅错题本。在复习时，将以前做过的试卷或者收集起来的错题本拿出来，多看看里面经常会犯错， 而且容易忽略的基础性错误，避免在高考时又在同样的地方摔倒，尽量做到会做的题目，就拿满分，不会 做的题目，分析一下哪些步骤会做，争取拿分，特别是理科题，不要因为是难题就完全放弃，而是在考试 的时候，看哪些步骤会，就写上去，题目是按步骤给分，多争取一个步骤，就多争取一分，就相当于为上 理想大学多向前迈进了一步。 5.适当做题，掌握技巧。在临近高考前，会发现越来越多的模拟题，特别是各个地方传来的所谓高考热 点，这时候自己要有所针对性地做一些相应的模拟题，但切记过多，一个星期在规定的时间内完整做完2 到3套模拟题即可，关键在于保持自己的作战心态，从做题中给自己一个宏观上的分析，可以找出自己在 做题过程中所遇到的问题，避免在考场上的重现，提高自己的应试能力，做到知己知彼。 心理调整 1.给自己积极的心理暗示。每天早上起床，面对着镜子微笑，提升自信心，保持良好的心态，就算跟同 学打招呼，也露出自信的微笑，一定要相信自己，只要努力付出了，就无怨无悔。高考只是学习之旅的一 个驿站，考得好与不好只是暂时的一个经历而已，重要的是在这12年的学习中，培养的思考能力与学习能 力，以后的人生之路还很长很长。 2.不跟学习成绩好的攀比。五指伸出有长短，每个人都有每个人的优缺点，有长处也有短处，而且每个 人的学习方法不同、天赋不同、后天成长也不同，根本就不存在可比性，每天只要跟自己比就好，是否今 天又发现了自己存在丢分的环节，是否又发现了自己可以在哪些环节上进行加分，只有不断地剖析挖掘自 己，自然而然就能够更加客观地看待这次高考。 3.放松心情，别给自己太大压力。高考几乎是每个人都会经历的一次考试，当然心态看个人，主要靠自 己调整，越是临近高考，越是要跟学长、老师或者家人进行心理上的沟通，把心中的烦闷跟他们讲，把遇 到的心理压力释放出来。作为过来人，他们会给出当年高考是怎么一步步走过来的，这样有了一个借鉴性 的经验，自然心情就会舒畅很多，切忌什么事情都往自己身上推，对自己过不去，就是对自己的未来过不 去，多多沟通交流，才能不断解惑释压。 4.劳逸结合。在临近高考，学生切忌整天除了睡觉的时间，其余都花在课本上面。每天给自己定好一个 复习计划，看完书就到外面走走、散散步、跑跑步、聊聊天或者打打球，让大脑休息一下，持续地看书做 题，有时会让大脑处于一个紊乱状态，可能有一些题目其实并不难，但却总是解不出。不知道同学们自己 - 133 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}有没有发现，当过了一两天之后，这些所谓的难题再拿出来做，会有一种豁然开朗的感觉，这就是需要劳逸 结合的目的所在。而且通过适当的运动，还可以增强体质，保持一个健康的体魄，避免高考时身体不适，导 致发挥失常，那才是前功尽弃，得不偿失。 2.高考前一天需要做哪些准备 高考对于考生和考生家长都是一次很重要的考试，考试中如果发生一点差错，就可能会对考生造成影 响，那在考前应该做好哪些准备工作，让我们有备无患呢？ 1.考场踩点。在高考前，考生最好能够去考场踩点，以便在高考当天迅速找到考场，避免因考场找不到 而造成的心理焦虑，我们去踩点时要注意考场在哪栋楼、哪一层、哪个教室，座位大约在哪，洗手间在教 学楼的哪个位置，从我们的住处到考场需要多长时间，要使用什么交通工具，等等。这些如果考场不是在 本校的，学校一般都会统一安排时间让考生提前到考场适应环境。 2.准备好考试用品。最重要的准考证、身份证，文具(包括签字笔、2B铅笔、橡皮、三角板、直尺、圆 规等)，手表，着装，水和雨具。这些可以统一放在一个文件袋中，方便寻找。 3.调整作息时间。为了在高考时，能够有更好的发挥，在考前一天，复习的强度不宜过大，休息好大脑 - 134 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}才能在考试时充分发挥。 4.记清考试规则。在考前一定要记住高考的规则，不要带考试禁止的东西进入考场，考号、姓名要写在 规定处，不要带草稿纸等出考场。考号姓名以及答题卡涂写方式可以在平常的模拟考试中演练。 5.调整心态，积极面对高考。有一个良好的心态，对于高考无比重要，很多考生会因为高考的巨大压力 寝食难安，在考前，考生可以通过自我暗示、与人沟通、转移注意力等方式调整自己，让自己带着最佳心 态进入考场！ 考场注意篇 1.高考遇到不会的题怎么办？ 考场上遭遇棘手难题该如何破局？难道要放任珍贵分数从指缝间溜走？绝不！纵然身处绝境亦要奋起 突围！须知高考战场一分之差便可跨越千军万马，这绝非危言耸听。正因如此，我们必须在考前铸就万全 之策，方能在试炼降临之际保持头脑清明如鉴，决策精准似刃，将每一个可能斩获的分数牢牢攥在手中。 不管你考前准备的如何充分，高考考场上，真正较量的已经是心态遇到不会做的题，一般都会有压力，情 绪紧张。此时冷静下来，先别自己吓自己。 在考试中遇到不会做的题目是很正常的现象，但过度紧张只会削弱我们的判断力。正如专家所建议的， 保持冷静的心态对于考试表现至关重要。紧张不仅容易导致错误，还可能使我们的时间感知变得扭曲，从 而影响整体表现。自己以为才患考了一两分钟，其实慌慌忙忙的已经过了十分钟。一看表，妈呀更紧张了， 于是只好放弃。 考了这么多年的试，每个人都会有自己处理紧张情绪调整心态的办法，但要是你还无法处理好，说明 自己的方法不管用。 今天讲几个怎么在考场调整情绪的方法，希望能给大家一些启发， 第一招：直面紧张，解决问题 按照常理，我应该劝大家握紧拳头对自己说，我不紧张我一点都不紧张。我不知道对你有没有用！ 反正对我没什么帮助，就像试图用纸包住火焰，只会让事情更加明显。情绪需要发泄，考场上争分夺秒， 与其花时间安慰着自己，不如承认事实。就是不会做就是很紧张，就让自己顺利发个抖呗，几秒就抖完了， 抖完会发现，也没什么好紧张的。就好像发火一样，火气发完也就几秒的事，压着火可能几天心里都不舒 服。正视问题，才能解决问题！直面紧张，才能克服紧张！ 第二招：放空情绪，一心考试 每次考试，我会有意识训练自己，这是在考试，考完了你可以紧张可以大哭，但考试这两个小时什么 都不许想，只一心一意考试就好。做题都没时间好么，哪有时间紧张有任何情绪都直接忽略，就好像自己 - 135 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}是在执行任务的代码一样，考试无非是把自己会做的掌满分，有任何情绪都直接忽略，就好像自己是在执 行任务的代码一样，考试无非是把自己会做的拿满分不会做的拼命多掌分。看到简单的题，不高兴也就没 有粗心的可能，看到不会做的题，先想到的不是紧张伤心，也就能全力以赴。 第三招：用好紧张情绪，或许超常发挥 紧张即压力，利用好了，压力就是动力。怎么把压力转化为动力，个人觉得一定要保持积极的心态。 这一点好像和第二点有矛盾，但高考不是儿戏，谁也不想再来一次，总是要想办法做到最好。多年的考试 历练，让大脑锻炼出了一种能力，只要运转正常，考试时便能如同拥有多个开关的机器，根据需要灵活切 换状态。高考前仅剩的这几天，不需要想太多，高考，也不需要想太多。面对一张试卷，你的目标就是逐 分攻克，将其一一收入囊中。这和打机的时候不是很像么，一关一关的闯下去，一级一级的升上去。为什 么电脑运行这么高效还鲜少出错？因为每道程序只按部就班执行自己的任务就好了。 第四招：随机应变，忽略形式 先易后难，先把能掌的分掌下从来都是重点。不必固执于难题，要学会灵活应对。高考最终看的是总 分，至于具体哪道题得分哪道题失分，并不重要。像数学最后一道大题最后两小结这种高难度，见好就收 吧，把会做的步骤写完就好。不纠结了自然也就可以从容面对了。对于会做的题目，要确保拿满分。对于 不会做的，要想方设法，灵活运用各种技巧。实在不行的，回去检查！但是记得改答案一定要确认又确认， 别冲动。 - 136 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}2.如何克服丢失不该丢的分 每次考试，总会有很多的学生丢失本不该丢的20分——这些分数不是败给难题，而是输在草稿纸上跳 错的数字，答题卡上错位的选项，审题时漏看的"不"字。下面，我们就来共同锻造这把名为"细心"的利剑。 一、认知突围：失误的本质是态度偏差 当我们反复强调"认真审题"却收效甚微时，就像对着雾中灯塔喊话。某重点中学追踪研究发现，习惯性 失误者往往存在认知误区：把"马虎"归咎于偶然，将"粗心"美化为性格。殊不知，这恰如运动员轻视热身， 医生忽略消毒，本质都是对专业精神的怠慢。唯有正视失误背后的态度问题，方能从根本上斩断粗心的根 源。如同工匠雕琢璞玉，需耐心细致，步步为营。培养专注习惯，严谨对待每一处细节，让细心成为习惯， 而非偶尔的闪光。如此，方能剑指高分，无往不利。 请记住，高考本质是精确度的极限测试。就像航天器对接容不得毫米误差，我们的答题系统也需要建 立防错机制。从日常练习中嵌入细致入微的检查流程，到考场上的冷静自省，每一步都是对细心的锤炼。 唯有如此，才能在关键时刻避免低级错误，让每一次落笔都精准无误，最终成就高分梦想。 二、双重自我：构建内在监督系统 想象考场中存在两个"你"：一个是执笔答题的战士，另一个是手持放大镜的监考。这种"双重自我员工 法"已在飞行员训练中应用数十年。具体操作时，请在每个解题节点启动15秒速查程序：读题时标注题眼如 同考古学家标记甲骨文，书写时笔尖轻点标点似雕刻家收刀，计算时复述过程像会计核对账目。如此，内 外兼修，形成严密的自我监控体系，确保每一步都精准无误，让细心成为潜意识中的本能反应。久而久之， 习惯成自然，失误自然遁形，高分亦如探囊取物。 某位清华学长分享的案例令人震撼：他专门训练"视线回扫"技能，像复印机扫描般在解题后自动回看关 键数据。这种机械性的重复看似笨拙，却在高考数学中帮他挽回12分，相当于全省排名跃升15000位。 三、四维锚定：让技巧成为肌肉记忆 "读写解算"四步口诀犹如四把钥匙：读题时画出逻辑树状图，书写时实施"三秒延迟"策略，理解时建立 知识点超链接，计算时启动逆向验证程序。就像钢琴家形成肌肉记忆，我们需要让这些动作成为解题的默 认设置。 建议同学们在模拟考中创造"高压实验室"：故意设置干扰项训练专注力，用倒计时器制造紧迫感，甚至 尝试在嘈杂环境中解题。这些刻意练习，终将锻造出在考场上稳如磐石的定力。 四、执行升华：从知道到做到的最后一公里 知道凌晨四点的洛杉矶不算什么，重要的是每个清晨准时响起的闹钟。建议建立"失误日志"，像科学家 记录实验数据般追踪每个错误。某重点班实践表明，坚持21天记录的学生，失误率下降67%，这比任何励 - 137 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}志标语都更具实证力量。 请将每次练习视为高考实景演练：从填涂答题卡时铅笔的倾斜角度，到草稿纸的分区策略，再到水杯 摆放的位置，都要形成条件反射。记住，战场上没有临时起意，只有千锤百炼的肌肉记忆。 同学们，当你们走出考场时，最欣慰的不会是攻克了某道难题，而是在每个细节处都做到了极致。那些看 似微不足道的15秒检查，终将汇聚成改变命运的洪流。让我们以工匠精神雕琢每个解题步骤，让细心成为 刻进DNA的考试基因！ 如此，每一次练习都是对自我极限的挑战，每一次检查都是对完美细节的追求。 - 138 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}考后注意篇 1.高考结束后要注意什么？ 2025 年高考总算考完咯，同学们眼瞅着就要迎来舒舒服服的“考后”小日子啦。在美滋滋享受假期的当 儿，可千万得把“安全第一”记在心头呀！ 一、预防溺水 炎热夏季，我们应避免因追求凉爽而忽视安全，切勿前往不熟悉或缺乏安全措施的水域游泳。若不幸 遇到溺水事故，我们不应仓促下水救援，而应先准确评估自己的救援能力，并采取科学合理的救援方法。 二、防雷雨、山洪 夏季暴雨等极端天气事件频发，提醒各位同学需提高警觉。建议密切关注天气预报信息，当遭遇台风、 暴雨、雷暴等恶劣天气状况时，应尽量减少外出活动。在雷雨天气中，应避免靠近电线杆、变压器、户外 广告牌、桥洞、下沉式立交桥、树木等潜在危险区域。若必须在积水中行走，请务必留意周遭环境，以预 防不慎跌入窨井或坑洞等意外发生。 三、交通安全 高考结束后，众多学子倾向于选择参与外出聚会或旅游活动。在出行过程中，必须高度重视安全问题。 特别需要指出的是，未成年人驾驶机动车辆不仅存在极大的安全隐患，而且违反了法律规定。因此，我们 应当恪守交通法规，乘坐车辆时务必系好安全带，牢记“安全带等同于生命带”的重要性。 四、防诈骗 高考结束后，若接到自称来自高校、教育、财政等部门的工作人员的电话或信息，声称将发放“国家助 学金”、“返还义务教育费”、“助学扶助款”，或进行非正规渠道的招生宣传，考生及家长应保持警惕，切勿 轻信。应主动与当地教育部门或学校联系核实。请注意保护个人隐私信息，准考证、身份证、考生号和密 码、成绩单或成绩查询页面、志愿填报信息等切勿随意公开。不要轻易点击不明链接，通过官方网站核实 分数和录取信息。在参加暑期社会实践前，请务必深入了解实践单位的具体情况，明确相关的法律条款和 - 139 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}规定，以防上当受骗。在外出游玩时，不轻信陌生人，不随意透露个人信息。 五、最迫切：放松心情，调整作息 请确保充分休息，并对个人物品进行有序整理。对于已使用的资料，应进行妥善分类处理，可以选择 保存、出售或转赠给后辈。网络上流传的诸如撕毁书籍、试卷等极端宣泄行为，既不环保，亦非明智之举。 考试结束后，在放松身心的同时，应及时调整心态，以积极的姿态迎接人生的新篇章。 放松身心并不等同于放纵自己：追剧、通宵打游戏、日夜颠倒等不良生活方式应坚决避免，备考期间 养成的良好作息习惯需继续保持，并注重加强锻炼，以增强自身免疫力。 六、最理智：合理规划未来 在准备填报志愿的过程中，必须深入探究所选专业的课程内容、就业趋势及职业成长路径；对于个人 感兴趣的专业领域，在掌握其学术背景与行业发展趋势的基础上，应积极向行业专家或教师寻求指导，审 慎权衡其优劣，并进行深入的交流与讨论。 七、最感悟：回顾过去，展望未来 对高中三年的时光进行系统性的回顾，撰写文章。深思高中生涯，记录下那些珍贵的回忆，甚至可以 尝试创作小说，重温那些曾经邂逅的人物与事件。回顾过去，展望未来，让青春的梦想与理想在心灵中飞 翔，最终将它们转化为文字，这将成为我们未来珍贵的精神财富。 八、最走心：静心阅读 何不利用这个时机，遨游于书海，尽情领略阅读那些吸引你的书籍？特别是那些经典名著，它们能够 拓展我们的思路，拓宽我们的眼界。 九、最感恩：向陪伴成长的人表达谢意 感恩之情永远都不会缺席。 高考结束之际，对默默奉献的父母道一句，“感恩你的关怀”。 六月时分，这既是告别的季节，也是表达谢意的时刻，感谢老师，感谢父母，感谢那些始终给予支持、 守护和无声付出的亲朋好友。 2.高考志愿填报十大铁律 高考结束并非终点，而是人生关键的转折点！志愿填报得当，分数才能发挥最大价值；一旦失误，高 分也可能遭遇“滑铁卢”。面对院校选择、专业设置和录取规则的复杂性，许多家庭容易感到困惑，甚至因盲 目跟风或信息不对称而错失良机。今天，我们整理了高考志愿填报的十大原则，希望帮助大家在填报时更 加理性、科学，为孩子的未来铺就一条明确的道路。 - 140 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}一、普通家庭求稳：优先考虑医学、军校、师范生等专业，这些领域通常能提供稳定且有保障的职业 发展。 二、富裕家庭传承：选择金融、经济、管理等专业，有助于延续家族的商业传统和财富积累。 三、追求高薪起点：选择名校的电子通信、计算机等专业，这些领域发展潜力大，薪资待遇优厚。 四、人工智能、大数据方向：名校的师资和资源更具优势，普通院校在这些领域相对竞争力不足。 五、非名校慎入经管：缺乏名校背景，在竞争激烈的经管领域可能会面临较大挑战。 六、谨慎对待“生化环材”：这些专业需要深入的学术研究才能有良好发展，不打算读硕博不建议轻易 选择。 七、农林、地矿、石油和土建：这些专业通常需要在艰苦环境中工作，需做好心理准备。 八、艺术类专业：需要天赋、资金和人脉支持，成功并非仅靠努力就能实现。 九、医学、法学：道路漫长但前景广阔，医学需要长期学习，法学还需考取相关证书。 十、认清自我最关键：天才追求改变世界，普通人应追求一份好工作，志愿填报需结合自身特点和目 标。 志愿填报既是一场信息战，也是一场心理战。此外，还需综合考虑个人兴趣、能力、家庭背景等因素， 科学分析院校录取数据，合理规划志愿梯度，避免盲目追求“热门专业”或“名校光环”。愿每位考生和家长都 能在填报过程中保持冷静，理性选择，为孩子的未来奠定坚实基础。 可能这才是高考的真谛吧：它不一定能决定你 未来的路，但绝对记录了你青春里最闪亮的瞬间。 - 141 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}2025 年新高考数学终极押题卷 注意事项： 1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。 2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需 改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在 本试卷上无效。 3.考试结束后，将本试卷和答题卡一并交回。 一、选择题（本题共8小题，每小题5分，共 40分.在每小题给出的四个选项中，只有一项是 符合题目要求的） 1．已知集合A  x∣5 x3 5  ,B{3,1,0,2,3}，则A B（ ）  A．{1,0} B．{2,3} C．{3,1,0} D．{1,0,2} 2．记S 为等差数列a 的前n项和，若a 3,S 3，则S （ ） n n 3 3 12 A．144 B．120 C．100 D．80 3．已知抛物线y2 2px(p0)的焦点为F，过点F的直线与该抛物线交于A，B两点， AB 10，AB的中 点横坐标为4，则p（ ）． A．2 B． C． D． 2 3 4 4 3 4．已知一组数据为1，1，3，4，5，7，10，11，若n为这组数据的70%分位数，则(2xy)n的展开式中x4y3 的系数为（ ） A．280 B．280 C．560 D．560 ln( x21x) 5．函数 f(x) 的图象大致为（ ） exex A． B． C． D． b2 tanB 6．在  ABC中，角A、B、C所对的边为a、b、c若  ，则  ABC的形状是（ ） c2 tanC A．等腰三角形 B．直角三角形 C．等腰三角形或直角三角形 D．等腰直角三角形 - 142 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}7．已知函数yex的图象在点Pa,b（其中a2）处的切线与圆心为Q1,0的圆相切，则圆Q的最大面积 是（ ） A．π B．2π C．3π D．4π 8．莱洛三角形，也称圆弧三角形，是一种特殊三角形，在建筑、工业上应用广泛．如图所示，分别以正三 角形ABC的顶点为圆心，以边长为半径作圆弧，由这三段圆弧组成的曲边三角形即为菜洛三角形，已知    正三角形ABC的边长为1，点P为AB的中点，则PC(PAPB)的值为（ ） 1 3 A．1 B．2 3 C． D． 2 2 二、多项选择题（本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合 题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.） 9．（本题6分）若复数z满足1iz15i（i是虚数单位），则下列说法正确的是（ ） A．z的虚部为2i B．z的模为 13 C．z的共轭复数为32i D．z在复平面内对应的点位于第三象限 10．我国南宋数学家杨辉1261年所著的《详解九章算法》一书中展示了二项式系数表，数学爱好者对杨辉 三角做了广泛的研究．则下列结论正确的是（ ） A．第6行、第7行、第8行的第7个数之和为第9行的第8个数 - 143 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}B．1C1 C2C3 C3 5 6 7 8 C．第2020行的第1010个数最大 D．第12行中从左到右第2个数与第3个数之比为2:11 11．已知正方体ABCDABCD 的边长为2，M为CC 的中点，P为侧面BCC B 上的动点，且满足AM //平 1 1 1 1 1 1 1 面ABP，则下列结论正确的是（ ） 1 A．AM BM B．CD //平面ABP 1 1 1 2 2 13 C．AM 与AB 所成角的余弦值为 D．动点P的轨迹长为 1 1 3 3 三、填空题（本大题共3小题，每小题5分，共15分.） 12．已知平面向量a5,1,b  1,1,c1,k，若  ab  c ，则k ． x2 y2 13．已知双曲线C:  1(a0,b0)的左、右焦点分别为F,F ．O为坐标原点，点M 在双曲线C的 a2 b2 1 2 FM 5 一条渐近线l上，且FM l，若 2  ，则双曲线的渐近线方程为 . 1 FM 2 1 14．某大学开设了“九章算术”，“数学原理”，“算术研究”三门选修课程．甲、乙、丙、丁四位同学进行选课， 每人只能等可能地选择一门课程，每门课程至少一个人选择，甲和乙选择的课程不同，则四人选课的不 同方案共有 种；若定义事件A为甲和乙选择的课程不同，事件B为丙和丁恰好有一人选择的是“九 章算术”，则PB∣A ． 四、解答题(本大题共5小题，共77分.解答应写出必要的文字说明、证明过程或演算步骤.) 15．（本题13分）某人工智能公司从某年起7年的利润情况如下表所示． 第x年 1 2 3 4 5 6 7 利润y/亿元 2.9 3.3 3.6 4.4 4.8 5.2 5.9 (1)计算出y与x之间的相关系数（精确到0.01），并求出y关于x的回归直线方程． (2)根据回归直线方程，分别预测该人工智能公司第8年和第9年的利润． 16．（本题15分）在 ABC中，角A，B，C所对的边分别为a，b，c，且  - 144 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}    2asinAb 2sinB 3sinC c 2sinC 3sinB ． (1)求角A的大小； 2π (2)若b2 3，c2，点D为边BC上一点，且ADC  ，求△ABD的面积大小． 3 17．（本题15分）如图1，等腰梯形ABCD中，AB//CD,CD AB2,E,F 分别为AB,CD的中点，且EF  6， 将梯形AEFD沿EF翻折至梯形AEFD，使得平面AEFD 平面BEFC，得到如图的多面体ABEDCF， 1 1 1 1 1 1 且BF  AC. 1 (1)证明：A,B,C,D 四点共面； 1 1 (2)求BE的长； (3)在DC上取一点P，使得平面EFP平面ABCD ，求平面BFP与平面BEFC夹角的余弦值. 1 1 1 - 145 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}18．（本题17分）已知点A2,0为椭圆E: x2  y2 1ab0的右端点，椭圆E的离心率为 3 ，过点 a2 b2 2 P2,2的直线l与椭圆交于B、C两点，直线AB、AC分别与y轴交于M、N 点. (1)求椭圆E的标准方程; (2)试判断线段MN的中点是否为定点，若是，求出该点纵坐标，若不是，说明理由. n 19．（本题17分）定义：a i a 1 a 2   a n ，其中nN*． i1 (1)求证：当x0时，lnxx1（当且仅当x1时取等号）． n  1  (2)对于任意正整数n，是否存在正整数m，使得不等式 1 m恒成立？若存在，请求出m的最小  2i  i1 值；若不存在，请说明理由． n a2b2  k 1 (3)若正项数列a n 满足2a n1 ba n 2b2，0ba 1 ，nN*，求证： k1 k  2a b1  ． j1 j1 - 146 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}确认过眼神，这就是你想要做的题！ 2025 年新高考数学终极押题卷（解析版） 大厦巍峨意似铁，三年苦干血汗彰。 定怀信念乘风进，稳操胜券写锦章。 注意事项： 1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。 2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需 改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在 本试卷上无效。 3.考试结束后，将本试卷和答题卡一并交回。 一、选择题（本题共8小题，每小题5分，共 40分.在每小题给出的四个选项中，只有一项是 符合题目要求的） 1．已知集合A  x∣5 x3 5  ,B{3,1,0,2,3}，则A B（ ）  A．{1,0} B．{2,3} C．{3,1,0} D．{1,0,2} 【答案】A 【详解】因为A  x|35 x 3 5  ,B3,1,0,2,3，且注意到1 352， 从而A B1,0.  2．记S 为等差数列a 的前n项和，若a 3,S 3，则S （ ） n n 3 3 12 A．144 B．120 C．100 D．80 【答案】B 【详解】因为S 3a 3，所以a 1，又a 3，所以d a a 2，则a a d 1， 3 2 2 3 3 2 1 2 1211 所以S 121 2120 12 2 3．已知抛物线y2 2px(p0)的焦点为F，过点F的直线与该抛物线交于A，B两点， AB 10，AB的中 点横坐标为4，则p（ ）． A．2 B． C． D． 2 3 4 4 3 【答案】2 x x 【详解】由抛物线定义知： AB x x  p10，而AB的中点横坐标为4，即 A B 4， A B 2 所以8 p10，即p2. 4．已知一组数据为1，1，3，4，5，7，10，11，若n为这组数据的70%分位数，则(2xy)n的展开式中x4y3 的系数为（ ） A．280 B．280 C．560 D．560 【答案】D 【详解】由870%5.6，得n7，则(2x y)7展开式中含x4y3的项为C3(2x)4(y)3 560x4y3，所以所 7 求的系数为560. ln( x21x) 5．函数 f(x) 的图象大致为（ ） exex A． B． C． D． 【答案】A - 147 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}  ln x21x 【详解】 x21x0恒成立，故 f(x) 的定义域为R， ex ex    1   ln x21x ln x21x ln x21x ， f x   f x exex exex exex 故 f(x)为奇函数，BD错误；   当x趋向于时，yex ex的增长速度远大于yln x21x 的速度，   ln x21x 故 趋向于0，C错误，A正确. f(x) ex ex b2 tanB 6．在  ABC中，角A、B、C所对的边为a、b、c若  ，则  ABC的形状是（ ） c2 tanC A．等腰三角形 B．直角三角形 C．等腰三角形或直角三角形 D．等腰直角三角形 【答案】C sinB b2 tanB sin2B cosB 【详解】在  ABC中，由 c2  tanC 及正弦定理得 sin2C  sinC ，而sinA0,sinB0， cosC 整理得sinBcosBsinCcosC，即sin2Bsin2C，而0 Bπ,0C π， π 则02B2π,02C 2π，因此2B2C或2B2Cπ，即BC或BC ， 2 所以 ABC是等腰三角形或直角三角形.  7．已知函数yex的图象在点Pa,b（其中a2）处的切线与圆心为Q1,0的圆相切，则圆Q的最大面积 是（ ） A．π B．2π C．3π D．4π 【答案】B 【详解】依题意，切点P  a,ea ，yea，k ea， 所以切线为：yea eaxa，即eaxy1aea 0， 2aea 2aea 因为切线与圆相切，所以d r，d   , e2a 1 e2a1 2aea 2xex 所以r  ，令 f x x2， e2a 1 e2x1 2e2x 1xex e2x1 2xex 则 f(x) 2 e2x1  2 e2x 1 1xex e2x 1  2xe3x ex e2x x1     3  3 ， e2x1 e2x1 令 f(x)0，解得x0， 所以当x,0时， f(x)0，当x0,2时， f(x)0， 所以 f x在,0上单调递增，在0,2上单调递减， 2 所以 f x  f 0  2，即r  2， max 2 max 所以S πr 2 2π. max max - 148 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}8．莱洛三角形，也称圆弧三角形，是一种特殊三角形，在建筑、工业上应用广泛．如图所示，分别以正三 角形ABC的顶点为圆心，以边长为半径作圆弧，由这三段圆弧组成的曲边三角形即为菜洛三角形，已知正    三角形ABC的边长为1，点P为AB的中点，则PC(PAPB)的值为（ ） 1 3 A．1 B．2 3 C． D． 2 2 【答案】B 【详解】根据题意，以C为坐标原点，BC所在的直线为x轴，过点C且垂直于BC的直线为y轴，建立平 面直角坐标系，如图所示， 因为正  ABC的边长为1，且点P为AB的中点，所以PCB30， 1 3 3 1 点P在以C为圆心，BC为半径的圆上，则C(0,0),B(1,0),A( , ),P( , ), 2 2 2 2  3 1  3 1 3 1  3 1 所以PC ( , ),PA(  ,  ),PB( 1, )， 2 2 2 2 2 2 2 2   3 3    3 3 1 3 则PAPB( 3 , 1)，所以PC PAPB  ( 3 ) ( 1)2 3. 2 2 2 2 2 2 二、多项选择题（本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合 题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.） 9．（本题6分）若复数z满足1iz15i（i是虚数单位），则下列说法正确的是（ ） A．z的虚部为2i B．z的模为 13 C．z的共轭复数为32i D．z在复平面内对应的点位于第三象限 【答案】BC 15i 15i1i 1i5i5i2 64i 【详解】由1iz15i，所以z    32i， 1i 1i1i 1i2 2 所以z的虚部为2，故A错误； z  3222  13，故B正确；z的共轭复数为32i，故C正确；z在复 平面内对应的点为3,2，位于第一象限，故D错误. 10．我国南宋数学家杨辉1261年所著的《详解九章算法》一书中展示了二项式系数表，数学爱好者对杨辉 三角做了广泛的研究．则下列结论正确的是（ ） - 149 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}A．第6行、第7行、第8行的第7个数之和为第9行的第8个数 B．1C1 C2C3 C3 5 6 7 8 C．第2020行的第1010个数最大 D．第12行中从左到右第2个数与第3个数之比为2:11 【答案】ABD 【详解】对于A：第6行，第7行，第8行的第7个数字分别为：1，7，28，其和为172836； 而第9行第8个数字就是36，故A正确； 65 765 876 对于B：因为1C1 C2C3 15  56，C3  56， 5 6 7 21 321 8 321 所以1C1 C2C3 C3，故B正确； 5 6 7 8 对于C：由图可知：第n行有n1个数字， n 如果n是偶数，则第 1（最中间的）个数字最大； 2 n1 n1 如果n是奇数，则第 和第 1个数字最大，并且这两个数字一样大， 2 2 所以第2020行的第1011个数最大，故C错误； 对于D：依题意：第12行从左到右第2个数为C1 12，第12行从左到右第3个数为C2 66， 12 12 所以第12行中从左到右第2个数与第3个数之比为12:662:11，故D正确； 11．已知正方体ABCDABCD 的边长为2，M为CC 的中点，P为侧面BCC B 上的动点，且满足AM //平 1 1 1 1 1 1 1 面ABP，则下列结论正确的是（ ） 1 A．AM BM B．CD //平面ABP 1 1 1 2 2 13 C．AM 与AB 所成角的余弦值为 D．动点P的轨迹长为 1 1 3 3 【答案】BCD 【详解】如图建立空间直角坐标系，设正方体棱长为2， 则A(0,0,2),A(0,2,2),B(0,0,0),M(2,1,0),P(x,y,0)， 1    所以AB(0,2,2),BP(x,y,0),AM (2,1,2)， 1 - 150 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#} 0bx2     由AM//平面ABP，得AM aABbBP，即2aby1， 1 1   2a2 化简可得：3x2y0，所以动点P在直线3x2y0上，       对于选项A：AM (2,1,2),BM (2,1,0),AMBM 221(1)(2)030，所以AM 与BM 不 1 1 1 垂直，所以A选项错误；对于选项B：CD //AB,AB平面ABP,CD 平面ABP，所以CD//平面ABP， 1 1 1 1 1 1 1 1    4 2 B选项正确；对于选项C：AB (0,0,2),cos AM,AB   ，C选项正确； 1 1 1 1 2 2212(2)2 3 4  对于选项D：动点P在直线3x2y0上，且P为侧面BCC B 上的动点，则P在线段PB上，P ,2,0， 1 1 1 1 3  4 2 2 13 所以PB   2202  ，D选项正确； 1 3 3 三、填空题（本大题共3小题，每小题5分，共15分.） 12．已知平面向量a5,1,b  1,1,c1,k，若  ab  c ，则k ． 【答案】2 【详解】ab  4,2，因为  ab  c ，所以  ab  c0，即42k 0，解得k 2. x2 y2 13．已知双曲线C:  1(a0,b0)的左、右焦点分别为F,F ．O为坐标原点，点M 在双曲线C的 a2 b2 1 2 FM 5 一条渐近线l上，且FM l，若 2  ，则双曲线的渐近线方程为 . 1 FM 2 1 4 21 【答案】y x 21 【详解】 FM 5 由 2  ，不妨设 FM 2m，则 FM 5m FM 2 1 2 1 因为FM l，由焦点到渐近线的距离就是b，可知b2m 1 2m 在直角OFM 中，cosFFM  1 2 1 c 4m24c225m2 4c221m2 2m 37 在F FM 中，cosFFM    则解得c2  m2 2 1 2 1 8mc 8mc c 4 37 21 21 b 4 21 故a2  m24m2  m2a m，所以  4 4 2 a 21 4 21 综上，渐近线方程为y x 21 14．某大学开设了“九章算术”，“数学原理”，“算术研究”三门选修课程．甲、乙、丙、丁四位同学进行选课， 每人只能等可能地选择一门课程，每门课程至少一个人选择，甲和乙选择的课程不同，则四人选课的不同 方案共有 种；若定义事件A为甲和乙选择的课程不同，事件B为丙和丁恰好有一人选择的是“九章算 术”，则PB∣A ． - 151 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}8 【答案】 30 15 【详解】四个人参加三门选修课程共有C2A3 36种方案，其中甲和乙选择的课程相同共有A3 6种方案， 4 3 3 所以甲和乙选择的课程不同共有C2A3A3 36630种方案； 4 3 3 事件A共有30种方案，以下考虑事件AB，即“甲和乙选择的课程不同，丙和丁恰好有一人选择的是九章算 术”，先从丙、丁两个人中选一个人选择“九章算术”，则有C1 2种方案， 2 若四个人中只有一个人选择“九章算术”，则甲、乙分别选择另外两门课程，有A2 2种方案， 2 丙、丁中没选择“九章算术”的也从另外两门中选择一门，有C1 2种方案， 2 根据分步乘法计数原理，共有A2C1 224种方案； 2 2 若四个人中有两人选择“九章算术”，则除了包含丙、丁中的一个人外，还包含甲、乙中的一个人，有C1 2 2 种方案， 其余两人分别选择另外两门课程，有A2 2种方案， 2 根据分步乘法计数原理，共有C1A2 224种方案； 2 2 根据分步乘法计数原理和分类加法计数原理，事件AB中共有C1 A2C1 C1A2 24416种方案， 2 2 2 2 2 nAB 16 8 根据条件概率公式，PB A   nA 30 15 四、解答题(本大题共5小题，共77分.解答应写出必要的文字说明、证明过程或演算步骤.) 15．（本题13分）某人工智能公司从某年起7年的利润情况如下表所示． 第x年 1 2 3 4 5 6 7 利润y/亿元 2.9 3.3 3.6 4.4 4.8 5.2 5.9 (1)计算出y与x之间的相关系数（精确到0.01），并求出y关于x的回归直线方程． (2)根据回归直线方程，分别预测该人工智能公司第8年和第9年的利润． 【答案】(1)0.99，yˆ 0.5x2.3 (2)第8年的利润为6.3亿元，第9年的利润为6.8亿元． 【详解】（1）由表中数据可得 1 x 12345674， 7 1 y 2.93.33.64.44.85.25.94.3， 7 7 x xy y142.94.3243.34.3343.64.3 i i i1 444.44.3544.84.3645.24.3745.94.314， 7 x x2 142242342442542642742 28， i i1  7  y y 2 2.94.32 3.34.32 3.64.32 4.44.32 4.84.32 i i1 5.24.32 5.94.32 7.08， 14 14 所以r 0.99，b ˆ  0.5, aˆ4.30.542.3， 28 7.08 28 回归直线方程为yˆ 0.5x2.3． （2）在回归直线方程中令x8，得yˆ 0.582.36.3， 因此预测第8年的利润为6.3亿元． 在回归直线方程中令x9，得yˆ 0.592.36.8， 因此可预测第9年的利润为6.8亿元． - 152 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}16．（本题15分）在 ABC中，角A，B，C所对的边分别为a，b，c，且      2asinAb 2sinB 3sinC c 2sinC 3sinB ． (1)求角A的大小； 2π (2)若b2 3，c2，点D为边BC上一点，且ADC  ，求△ABD的面积大小． 3 5π 3 3 【答案】(1)A (2) 6 7 【详解】（1）由正弦定理可得a2 b2c2 3bc， b2c2a2  3bc 3 根据余弦定理得cosA   ， 2bc 2bc 2 5π 又A0,π，所以A ． 6 （2）因为b2 3，c2， 又a2 b2c2 3bc，解得a2 7， a2c2b2 28412 5 7 由余弦定理得cosB   ， 2ac 222 7 14 2 5 7 21 于是sinB 1cos2B  1   ，   14 14   2π π  3 1 3 21 因为ADC  ，所以sinBADsin B cosB sinB ， 3 3  2 2 14 AB BD 在△ABD中，由正弦定理得  ， sinADB sinBAD 23 21 csinBAD 14 6 7 所以BD   ， sinADB 3 7 2 1 1 6 7 21 3 3 于是S  ABBDsinB 2   ， △ABD 2 2 7 14 7 3 3 所以△ABD的面积大小为 ． 7 17．（本题15分）如图1，等腰梯形ABCD中，AB//CD,CD AB2,E,F 分别为AB,CD的中点，且EF  6， 将梯形AEFD沿EF翻折至梯形AEFD，使得平面AEFD 平面BEFC，得到如图的多面体ABEDCF，且 1 1 1 1 1 1 BF  AC. 1 (1)证明：A,B,C,D 四点共面； 1 1 (2)求BE的长； (3)在DC上取一点P，使得平面EFP平面ABCD ，求平面BFP与平面BEFC夹角的余弦值. 1 1 1 - 153 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}6 【答案】(1)证明见解析(2)BE 2(3) 4 【详解】（1）因为平面AEFD 平面BEFC，平面AEFD 平面BEFCEF， 1 1 1 1 且DF EF ，DF 平面AEFD， 1 1 1 1 所以DF 平面BEFC，又EF CF， 1 以F 为原点，以FE,FC,FD 所在直线为x,y,z轴建立空间直角坐标系， 1 设BEa，易得E  6,0,0  ,F0,0,0,A  6,0,a  ,B  6,a,0  ,C0,a1,0,D 0,0,a1， 1 1       则BF   6,a,0 ,AC   6,a1,a ， 1   由BF  AC，则BFAC6aa10，解得a3（舍去）或a2， 1 1   则AB0,2,2,DC0,3,3， 1 1  3   则DC AB，则DC//AB， 1 2 1 1 1 即DC//AB，所以A,B,C,D 四点共面. 1 1 1 1 （2）由（1）知，BEa2.         （3）由（1）知，AC   6,3,2 ，AB0,2,2，EF   6,0,0 ，DC 0,3,3， 1 1 1    设DPDC0,3,301，则P0,3,33，则FP0,3,33， 1 设平面ABCD 的一个法向量为m  x,y,z ， 1 1 1 1 1 则     m m       A A   1   C B     2  y 6  x 1 2  z 3  y 1 0 2z 1 0 ，取y 1  6，得m   1, 6, 6  ， 1 1 1 设平面EFP的一个法向量为n  x ,y ,z ， 2 2 2  n  E  F   6x 0 则  n  F  P  3y 2  2 33z 2 0 ，取z 2 ，得n  0,1,， 1 由平面EFP平面ABCD ，则mn 61 60，解得 ， 1 1 2  3 3   1 3    则P0, , ，则BP 6, , ，又BF   6,2,0 ，  2 2  2 2 设平面BFP的一个法向量为p  x ,y ,z ， 3 3 3 则    p  B  P   6x 3  1 2 y 3  3 2 z 3 0 ，取x 2，得p   2, 6, 6  ， 3  p  B  F   6x 2y 0 3 3 易得平面BEFC的一个法向量为q  0,0,1， pq 6 6 则cosp,q   ， p  q 161 4 6 则平面BFP与平面BEFC夹角的余弦值为 . 4 - 154 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}18．（本题17分）已知点A2,0为椭圆E: x2  y2 1ab0的右端点，椭圆E的离心率为 3 ，过点 a2 b2 2 P2,2的直线l与椭圆交于B、C两点，直线AB、AC分别与y轴交于M、N 点. (1)求椭圆E的标准方程; (2)试判断线段MN的中点是否为定点，若是，求出该点纵坐标，若不是，说明理由. x2  1 【答案】(1) y2 1(2)是，MN的中点为0,  4  2 c 3 【详解】（1）由题意得  ，a2，又a2 b2c2， a 2 解得a2，b1，c 3， x2 所以椭圆E的标准方程为 y2 1； 4 （2）设Bx,y ，Cx ,y ， 1 1 2 2 因为直线l经过(2,2)且与椭圆交于BC两点，所以直线BC的斜率一定存在， 故设直线BC的方程为：ykxm，其中m21k， ykxm 由  x2 得：  14k2 x2 8kmx4m240，   y2 1  4 Δ64k2m216  14k2 m21  0，得k  3 ； 8 8km 4m24 𝑥 +x  ，xx  ， (cid:2869) 2 14k2 1 2 14k2 y  2y  又因为直线AB的方程:y 1 x2 ，得M0, 1 ， x 1 2  x 1 2  2y  同理N0, 2   x 2 2 2y 2y 由 1 + 2 = x 2 x 2 1 2 kx mx 2kx m(x 2) 2kxx m2kx x 4m 2 1 2 2 1 2 1 2 1 2 (x 2)x 2 xx 2x x 4 1 2 1 2 1 2 2k  4m24  8kmm2k4m  14k2 =2  4m24  16km4  14k2 8k4m 4k2m 4k41k =2   1 4m216km16k2 m24km4k2 41k2 8k1k4k2  1 故MN的中点为0, .  2 n 19．（本题17分）定义：a i a 1 a 2   a n ，其中nN*． i1 - 155 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}(1)求证：当x0时，lnxx1（当且仅当x1时取等号）． n  1  (2)对于任意正整数n，是否存在正整数m，使得不等式 1 m恒成立？若存在，请求出m的最小值；  2i  i1 若不存在，请说明理由． n a2b2  k 1 (3)若正项数列a n 满足2a n1 ba n 2b2，0ba 1 ，nN*，求证： k1 k  2a b1  ． j1 j1 【答案】(1)证明见解析；(2)存在，3；(3)证明见解析 1 1x 【详解】（1）设hxlnxx1， hx 1 ，  x x 当x0,1时，hx0；当x1,时，hx0． hx在0,1上单调递增，在1,上单调递减， hxh10， 当x0时，lnxx1，当且仅当x1时取等号． （2）由（1）可得lnx1 x，当且仅当x0时取等号， 1  1  1 当x ，kN*时，ln1  ， 2k  2k  2k n  1  n 1 1 ln1 ln 1 1，  2i  2i 2n i1 i1 n  1   1 1   1  n  1  ln1 ln 1 1   1  ln 1   2i   2 22   2n   2i  i1 i1 n  1  n  1  ln 1 1， 1 e，  2i   2i  i1 i1 n  1   1 1  1  135 当n3时， 1 1 1 1  2，  2i   2 22  23 64 i1 n  1  当n3时， 1 2,e，  2i  i1 n  1  存在正整数m，对于任意正整数n，使得不等式 1 m恒成立，  2i  i1 m的最小值为3． （3） 2a ba2b2，  n1 n a2b2 a2b2  a2b21  1 1 1 k  k  k   当k2时，有  k  2a b1   k  a2b21   k  a2b21   k1  a2b21   k  a2b21 ， j1 j j j j j1 j1 j1 j1 j1    n a k 2b2  n a k 2b2 a2b2 n  1 1  k1 k  2a j1 b1  k1 k  a2 j b21   a 1 2 1 b21  k2    k1  a2b21    k  a2b21    j1 j1  j j   j1 j1    1   a2b2 1 1 1 1  a 1 2 1 b21  a 1 2b21   k  a2b21     k  a2 j b21  ，  j  j1  j1  n a2b2  k 1 k1 k  2a b1  ． j1 j1 - 156 - {#{QQABBQIAggCgABAAABhCAwWQCgOQkBCCAYoGgFAYMAIAgQNABCA=}#}