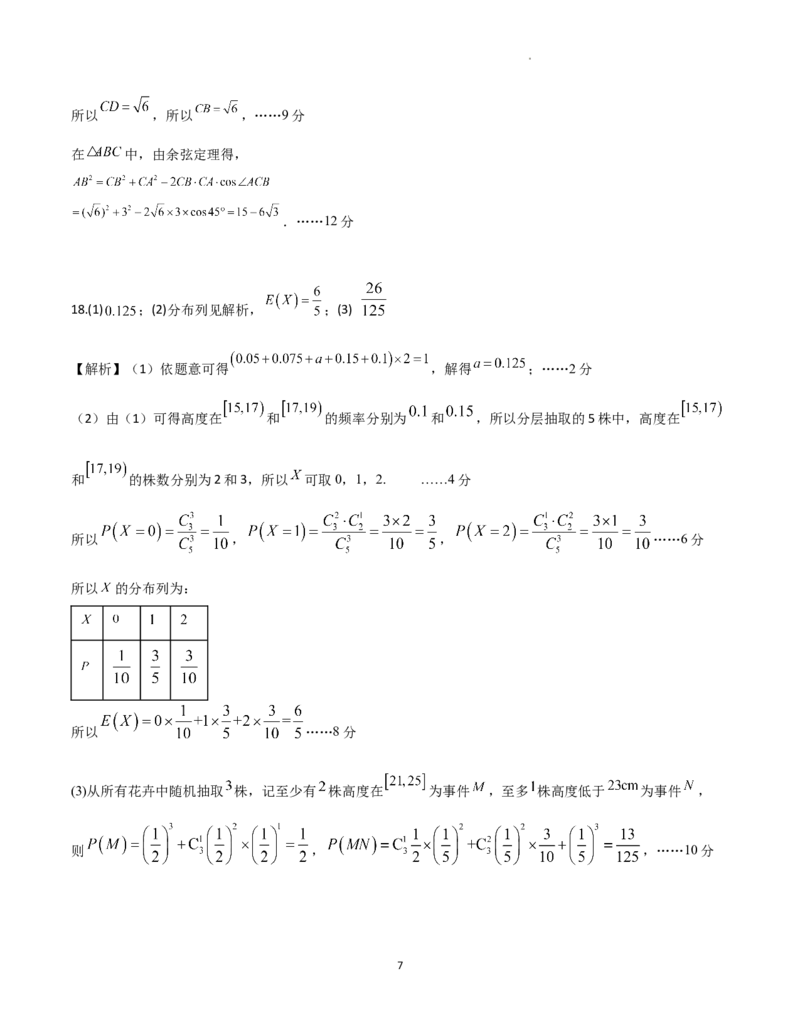文档内容
成都石室中学 2023-2024 年度下期高 2024 届三诊模拟
数学试题(理)参考答案
(总分:150分,时间:120分钟 )
第Ⅰ卷(共60分)
一、选择题(本题共12道小题,每小题5分,共60分)
1.B【解析】由 可得: , .又因为 ,
所以 或 .故选:B
2.C【解析】“ ”等价于“ ”,
所以
从而 ,显然A,B,C不共线,原条件等价于 是钝角.故选:C.
3. C【解析】根据题意,依次分析选项:
对于A,甲得分的极差为31, ,解得: ,A正确;
对于B,乙的平均数为 ,解得 ,B正确;
对于C,乙的数据为:12、25、26、26、31,其中位数是26,C错误;
对于D,甲的平均数 ,与乙的平均数相同,但根据茎叶图可得乙得分比较集
中,则乙得分的方差小于甲得分的方差,D正确;故选:C.
4.D【解析】因为 ,所以 ,共 项,
则 共 项,所以 比 共增加了 项,故选:
D
5. B【解析】由函数 ,
由此可作出 的函数图象,如图所示,
1
学科网(北京)股份有限公司对于A中,由 ,
所以 关于直线 不对称,所以A错误;
对于B中,由 ,所以B正确;
对于C中,由函数 图象可知, 不存在对称中心,所以C错误;
对于D中,因为 , , ,
所以函数 在 上不是单调递增函数,所以D错误.故选:B.
6. C【解析】 ,
而 ,故 .故选:C.
7.D【解析】由 ,则 ,则 , ,
依题意可得 且 、 、 ,所以 ,所以 ,
经验证,当 、 分别取 、 时 满足题意.故选:D
8.B【解析】将平面展开图还原为直观图,可得两个三棱锥拼接的六面体,它们共一个 底
面,且 两点重合,所以 与 相交, 故选:B
9. C【解析】设甲船到达泊位的时间为 ,乙船到达泊位的时间为 ,则 ,
2
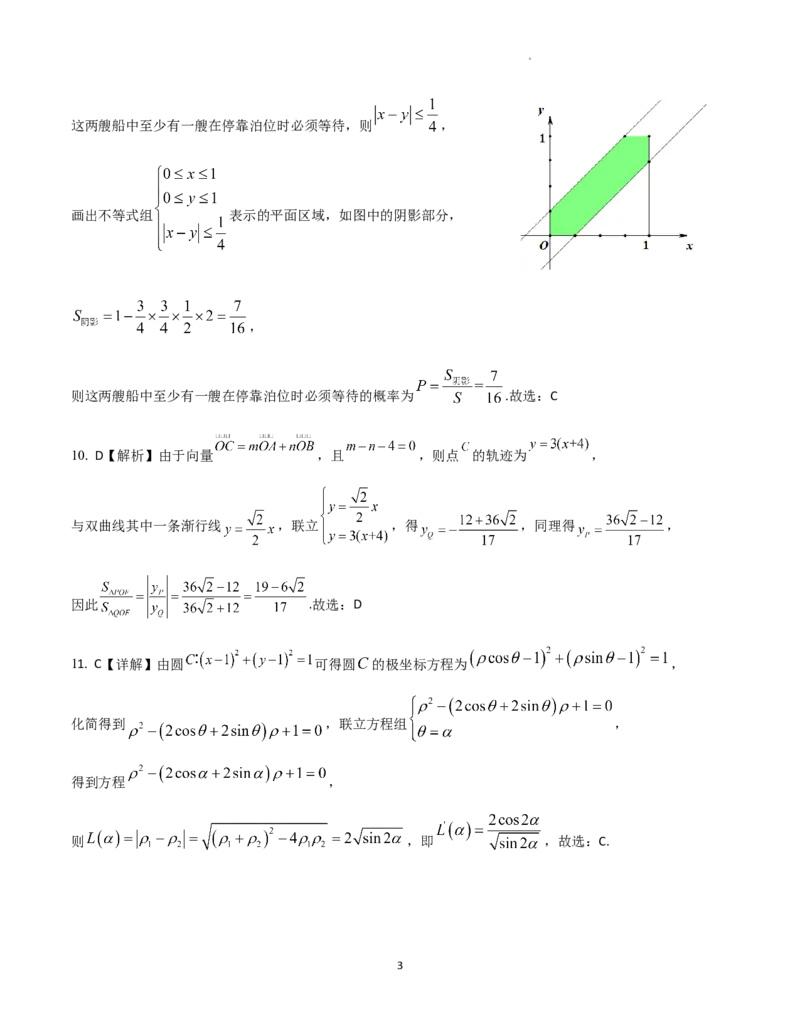
学科网(北京)股份有限公司这两艘船中至少有一艘在停靠泊位时必须等待,则 ,
画出不等式组 表示的平面区域,如图中的阴影部分,
,
则这两艘船中至少有一艘在停靠泊位时必须等待的概率为 .故选:C
10. D【解析】由于向量 ,且 ,则点 的轨迹为 ,
与双曲线其中一条渐行线 ,联立 ,得 ,同理得 ,
因此 .故选:D
11. C【详解】由圆 可得圆 的极坐标方程为 ,
化简得到 ,联立方程组 ,
得到方程 ,
则 ,即 ,故选:C.
3
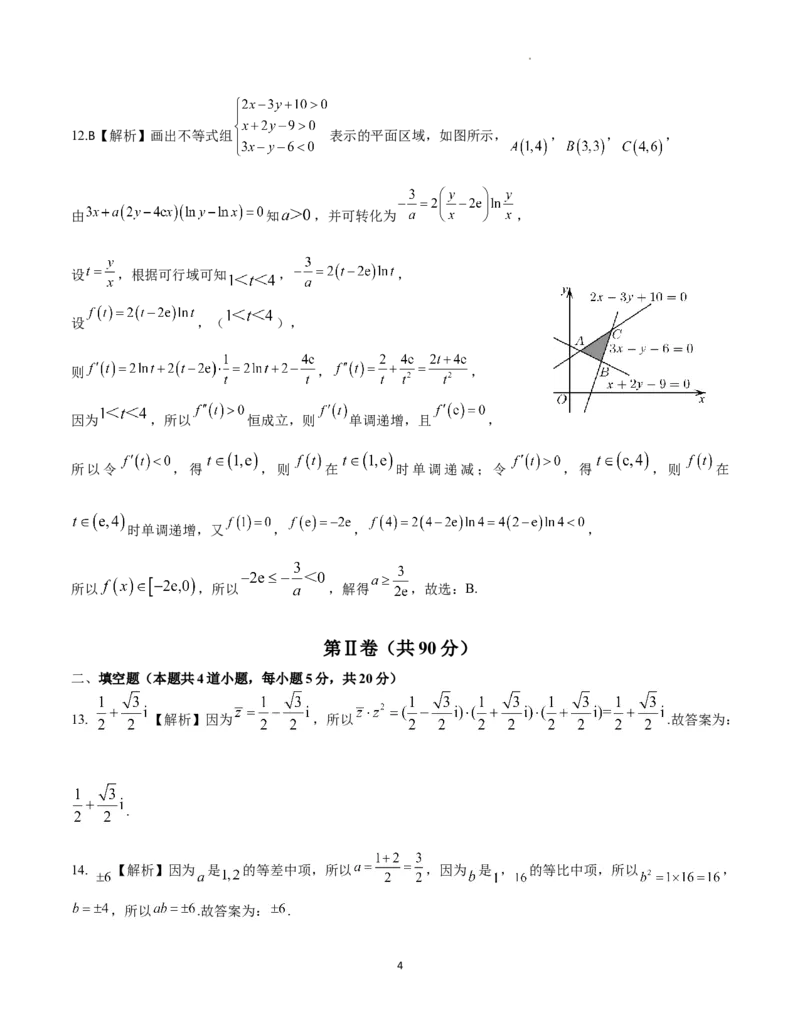
学科网(北京)股份有限公司12.B【解析】画出不等式组 表示的平面区域,如图所示, , , ,
由 知 ,并可转化为 ,
设 ,根据可行域可知 , ,
设 ,( ),
则 , ,
因为 ,所以 恒成立,则 单调递增,且 ,
所以令 ,得 ,则 在 时单调递减;令 ,得 ,则 在
时单调递增,又 , , ,
所以 ,所以 ,解得 ,故选:B.
第Ⅱ卷(共90分)
二、填空题(本题共4道小题,每小题5分,共20分)
13. 【解析】因为 ,所以 .故答案为:
.
14. 【解析】因为 是 的等差中项,所以 ,因为 是 , 的等比中项,所以 ,
,所以 .故答案为: .
4
学科网(北京)股份有限公司15. 【解析】令 即可求出 ,
令 即可求出 ,
,
结合 , , , , 可猜想 .
下面用数学归纳法证明:
当 时,由上述知 成立.
假设当 时有 ,
则当 时,不妨设 ,
.
所以 成立,所以 .
故答案为: .
16. 【解析】由教材章头图知识知道,用平面截对接圆锥所得截面边缘曲线是圆锥曲线.对于本题,如图,
水面到达杯底(底面圆“最高处”)的瞬间,水面边缘曲线是椭圆 ,作纸杯(圆台)的与水面垂直的轴截面
,则 是椭圆的长轴, 是椭圆的短轴. 是圆台的轴线,作 于
,则
,
,
5
学科网(北京)股份有限公司记 与 的交点为 的中点为 ,则 ,
,
,
,
由实际情形知,点 在圆台的过轴线 的中点 且与轴线垂直的截面圆上, .
由垂径定理知 垂直平分 , ,
记椭圆的离心率为 ,长半轴长、短半轴长、半焦距为 ,
则 .故答案为: .
三、解答题(本题共6道小题,共70分)
17.(1) (2)
【解析】(1)因为C点关于直线BD的对称点在直线AD上,
所以DB平分 ,所以 ,因为 ,所以 ,BC=CD,
所以 ‖ ,所以 ,
因为 , ,
所以 ,……3分
所以 .……6分
(2)因为在 中,由正弦定理得 ,
所以 , ,
6
学科网(北京)股份有限公司所以 ,所以 ,……9分
在 中,由余弦定理得,
.……12分
18.(1) ;(2)分布列见解析, ;(3)
【解析】(1)依题意可得 ,解得 ;……2分
(2)由(1)可得高度在 和 的频率分别为 和 ,所以分层抽取的5株中,高度在
和 的株数分别为2和3,所以 可取0,1,2. ……4分
所以 , , ……6分
所以 的分布列为:
所以 ……8分
(3)从所有花卉中随机抽取 株,记至少有 株高度在 为事件 ,至多 株高度低于 为事件 ,
则 , ,……10分
7
学科网(北京)股份有限公司所以 .……12分
19. 【解析】(1)函数 的定义域为 ,求导得 ,
当 时, 恒成立, 在 上单调递减,……2分
当 时,由 ,得 ,由 ,得 ,
即函数 在 上单调递减,在 上单调递增,……5分
所以当 时,函数 在 上单调递减,
当 时,函数 在 上单调递减,在 上单调递增. ……6分
(2)函数 的定义域为 ,求导得 ,
由 是 的极值点,得 ,即 ,……7分
,
而 ,则当 时, 单调递减,当 时, 单调递增,
所以当 时, 取得极小值. ……8分
设 ,求导得 ,
当 时, ,当 时, ,则函数 在 上单调递增,在 上单调递减,
因此 ,所以 .……12分
20.(1)证明见解析;(2) .
8
学科网(北京)股份有限公司【解析】(1)如图,平移线段 使得 与 重合,并将四面体 补成一个斜三棱柱.
则该斜棱柱的底面积 ,高 ,所以该斜棱柱的体积为定值. …….2分
此斜棱柱恰好可以分为两两底面积相同,高相同的三个三棱锥.
于是这三个三棱锥的体积都相等,都是斜棱柱的 .
所以四面体 的体积为 ,是定值. …….5分
(2)设球心是 ,并设 与平面 ,平面 的距离分别是 , .
由 可知, 在 , 的中垂面和 , 的中垂面的交线上.
设 的中点是 , 的中点是 .则由勾股定理得 .
注意到 ,所以 , , 共线,
且 平面 . …….8分
因为 ,且 , 与平面 的夹角均为 ,所以 .
而 、 、 、 、 均在球 上,所以 在以 点为圆心、以 为直径的
圆上(除去 、 两点).所以 .…….10分
于是 , ,所以 .…….12分
21.【解析】(1)由题意,得 且 ,又 ,
解得 ,所以椭圆 的标准方程为 . ……4分
9
学科网(北京)股份有限公司(2)设切线 的方程为 ,切线 的方程为 ,“环绕圆”的圆心D为 .
由“环绕圆”的定义,可得“环绕圆”的半径为1,所以“环绕圆”的标准方程为 .
因为直线 与“环绕圆”相切,则由点到直线的距离公式可得: ,……6分
化简得 .
同理可得 .
所以 是方程 的两个不相等的实数根,
所以 . ……8分
又因为“环绕圆”的圆心 在椭圆 上,所以代入椭圆方程 中,
可得 ,解得 .
所以 .……10分
又因为 且 ,所以 或 .
所以 或 ,所以 或 ,
所以 或 .
所以 的取值范围是 .……12分
选考题:共10分。请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
[选修4-4:坐标系与参数方程](10分)
10
学科网(北京)股份有限公司22. 【解析】(1)因为直线 的参数方程为 ,曲线 的极坐标方程为 ,
消去参数,直线 的普通方程为 , ……2分
曲线 的普通方程为: ,所以 的参数方程为 ( 为参数). ……4分
(2)由(1)有: 的参数方程为 ( 为参数),
由题意知,曲线 的参数方程为 ( 为参数),……6分
所以可设点 ,又直线 的普通方程为 ,
故点 到直线 的距离为: ,……8分
所以当 时, ,即点 到直线 的距离的最小值为 .……10分
[选修4-5:不等式选讲](10分)
23.【解析】(1)由 得: ,
当 时, ,解得 ;
当 时, ,解得 ;
当 时, ,解得 ;
综上,不等式的解集为 .……4分
11
学科网(北京)股份有限公司(2)证明: ,
因为 , ,即 , ,……6分
所以 ,
所以 ,即 ,所以原不等式成立. ……10分
12
学科网(北京)股份有限公司