专题20定序问题_2024-2025高三（6-6月题库）_2024年08月试卷_0816新高考数学题型全归纳之排列组合（20个专题）

专题 20 定序问题 例1．《数术记遗》是《算经十书》中的一部，相传是汉末徐岳（约公元2世纪）所著，该书主要记述了： 积算（即筹算）太乙、两仪、三才、五行、八卦、九宫、运筹、了知、成数、把头、龟算、珠算计数14种 计算器械的使用方法某研究性学习小组3人分工搜集整理14种计算器械的相关资料，其中一人4种、另两 人每人5种计算器械，则不同的分配方法有（ ） C4 C5 C5A3 C4 C5 C5A2 C4 C5 C5 A． 14 10 5 3 B． 14 10 5 2 C． 14 10 5 D．C4 C5 C5 A2 A3 A2 14 10 5 2 3 2 例2．今年3月10日湖北武汉某方舱医院“关门大吉”，某省驰援湖北“抗疫”的9名身高各不相同的医护人 员站成一排合影留念，庆祝圆满完成“抗疫”任务，若恰好从中间往两边看都依次变低，则身高排第4的医护 人员和最高的医护人员相邻的概率为（ ） 2 2 5 1 A． B． C． D． 7 9 14 7 例3．现有5名学生：甲、乙、丙、丁、戊排成一队照相，要求甲与乙相邻，且甲、乙、丁的左右顺序固定， 站法种数为（ ） A．36 B．24 C．20 D．12 例4．某次数学获奖的6名高矮互不相同的同学站成两排照相，后排每个人都高于站在他前面的同学，则共 有多少种站法（ ） A．36 B．90 C．360 D．720 例5．4名护士和2名医生站成一排，2名医生顺序固定，则不同的排法种数为（ ） A．480 B．360 C．288 D．144 例6．A，B，C，D，E五个字母排成一排，字母A排在字母B的左边（但不一定相邻）的排法种数为（ ）. A．24 B．12 C．60 D．120 例7．元宵节灯展后，悬挂有8盏不同的花灯需要取下，如图所示，每次取1盏，则不同的取法共有（ ）． A．32种 B．70种 C．90种 D．280种 例8．有6张卡片分别写有数字1、1、1、2、2、2，从中任取4张，可排出的四位数有________个. 1例9．将 这五个数字放在构成“W 型线段的 个端点位置，要求下面的两个数字分别比和 1,2,3,4,5, ” 5 它相邻的上面两个数字大,这样的安排方法种数为_______ . 例10．某活动中，有42人排成6行7列，现从中选出3人进行礼仪表演，要求这3人中的任意2人不同行 也不同列，则不同的选法种数为 （用数字作答）． 例11．一个房间的地面是由12个正方形所组成，如图所示.今想用长方形瓷砖铺满地面，已知每一块长方 形瓷砖可以覆盖两块相邻的正方形，即 或 ，则用6块瓷砖铺满房间地面的方法有_______ 种. 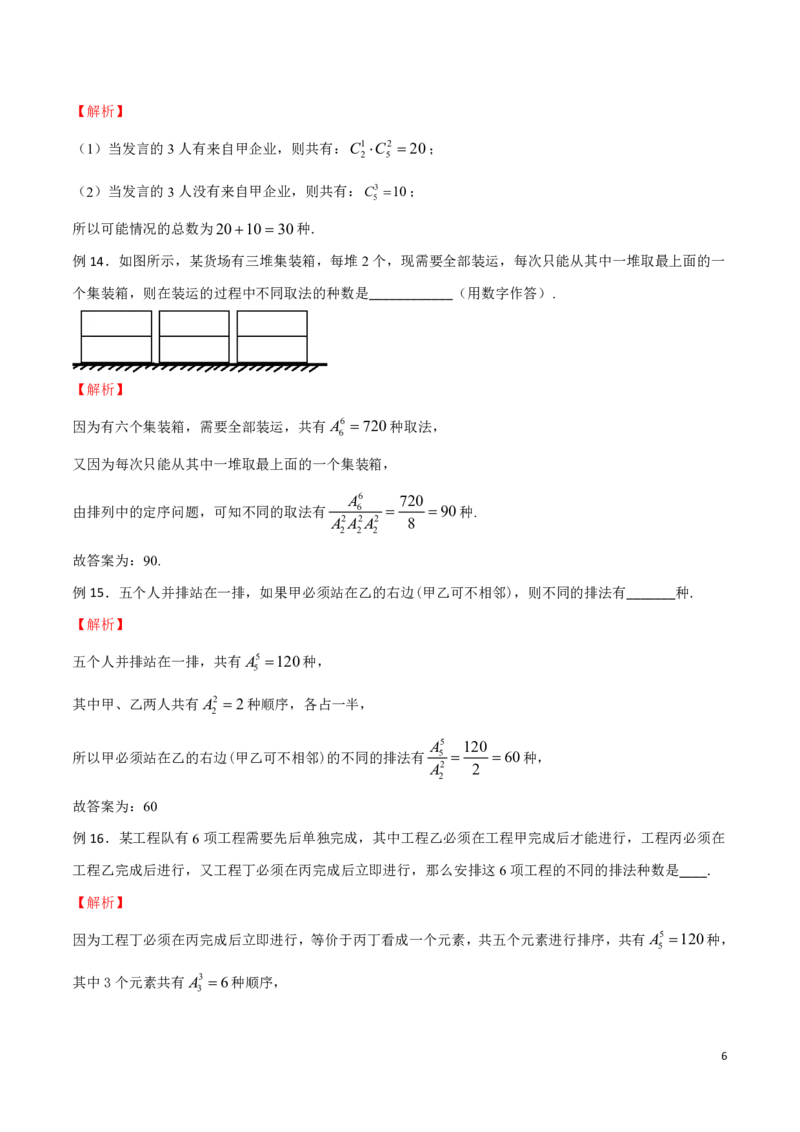例12．书架上某层有6本书，新买3本插进去，要保持原有6本书的顺序，有_____种不同的插法（具体数 字作答） 例13．某地环保部门召集6家企业的负责人座谈，其中甲企业有2人到会，其余5家企业各有1人到会， 会上有3人发言，则发言的3人来自3家不同企业的可能情况的总数为_______． 例14．如图所示，某货场有三堆集装箱，每堆2个，现需要全部装运，每次只能从其中一堆取最上面的一 个集装箱，则在装运的过程中不同取法的种数是____________（用数字作答）. 例15．五个人并排站在一排，如果甲必须站在乙的右边(甲乙可不相邻)，则不同的排法有_______种. 例16．某工程队有6项工程需要先后单独完成，其中工程乙必须在工程甲完成后才能进行，工程丙必须在 工程乙完成后进行，又工程丁必须在丙完成后立即进行，那么安排这6项工程的不同的排法种数是____. 例17．在班级活动中，4名男生和3名女生站成一排表演节目：（写出必要的数学式，结果用数字作答） （1）女生甲不能站在左端，女生乙不能站在右端，有多少种不同的排法？ （2）甲乙丙三人按高低从左到右有多少种不同的排法？（甲乙丙三位同学身高互不相等） 2（3）现在有7个座位连成一排，仅安排4个男生就坐，怡好有两个空座位相邻的不同坐法共有多少种？ 例18．（1）4本不同的书平均分成两堆，每堆两本，有几种分法？ （2）10人坐成一排，要求甲、乙、丙三人按从左到右的顺序就坐（不一定要相邻），有几种坐法？ 3专题 20 定序问题 例1．《数术记遗》是《算经十书》中的一部，相传是汉末徐岳（约公元2世纪）所著，该书主要记述了： 积算（即筹算）太乙、两仪、三才、五行、八卦、九宫、运筹、了知、成数、把头、龟算、珠算计数14种 计算器械的使用方法某研究性学习小组3人分工搜集整理14种计算器械的相关资料，其中一人4种、另两 人每人5种计算器械，则不同的分配方法有（ ） C4 C5 C5A3 C4C5 C5A2 C4 C5 C5 A． 14 10 5 3 B． 14 10 5 2 C． 14 10 5 D．C4 C5 C5 A2 A3 A2 14 10 5 2 3 2 【解析】 C4C5C5 C4C5C5 先将14种计算器械分为三组，方法数有 14 10 5 种，再排给3个人，方法数有 14 10 5 A3种，故选A. A2 A2 3 2 2 例2．今年3月10日湖北武汉某方舱医院“关门大吉”，某省驰援湖北“抗疫”的9名身高各不相同的医护人 员站成一排合影留念，庆祝圆满完成“抗疫”任务，若恰好从中间往两边看都依次变低，则身高排第4的医护 人员和最高的医护人员相邻的概率为（ ） 2 2 5 1 A． B． C． D． 7 9 14 7 【解析】 将身高从低到高的9个人依次编号为1，2，3，4，5，6，7，8，9， 则9号必须排在正中间，从其余8个人中任选4人排在9号的左边，剩下的4个人排在9号的右边，有C4 70 8 种， 当排名第四的6号排在最高的9号的左边时，从1，2，3，4，5中任选3个排在6号的左边，其余四个排 在9号的右边，有C3 10种，同理当当排名第四的6号排在最高的9号的右边时，也有10种， 5 所以身高排名第四的6号与最高的9号相邻的排法有10+10=20种， 20 2 所以身高排第4的医护人员和最高的医护人员相邻的概率为  . 70 7 故选：A. 例3．现有5名学生：甲、乙、丙、丁、戊排成一队照相，要求甲与乙相邻，且甲、乙、丁的左右顺序固定， 站法种数为（ ） A．36 B．24 C．20 D．12 【解析】 1因为甲与乙相邻，且甲、乙、丁的左右顺序固定， 所以可将甲和乙看作一个整体，共有1种站法， A4 再与其余三人进行排列，共有 4 12种站法. A2 2 故选：D. 例4．某次数学获奖的6名高矮互不相同的同学站成两排照相，后排每个人都高于站在他前面的同学，则共 有多少种站法（ ） A．36 B．90 C．360 D．720 【解析】 6个高矮互不相同的人站成两排， C2C2C2 后排每个人都高于站在他前面的同学的站法数为 6 4 2 A3 90， A3 3 3 故选：B 例5．4名护士和2名医生站成一排，2名医生顺序固定，则不同的排法种数为（ ） A．480 B．360 C．288 D．144 【解析】 4名护士和2名医生站成一排，共有A6种， 6 A6 720 又因为2名医生顺序固定，所以不同的排法种数为 6  360种. A2 2 2 故选：B. 例6．A，B，C，D，E五个字母排成一排，字母A排在字母B的左边（但不一定相邻）的排法种数为（ ）. A．24 B．12 C．60 D．120 【解析】 先5个字母全排列，由于字母A不是排在字母B的左边，就是排在字母B的右边两种情况，且这两种情况 A5 排列数相等，所以所求排列数为 5 60. 2 故选：C. 例7．元宵节灯展后，悬挂有8盏不同的花灯需要取下，如图所示，每次取1盏，则不同的取法共有（ ）． 2A．32种 B．70种 C．90种 D．280种 【解析】 因为取灯时每次只能取一盏，所以每串灯必须先取下面的灯， A8 即每串灯取下的顺序确定，取下的方法有 8 70种． A4A4 4 4 故选：B 例8．有6张卡片分别写有数字1、1、1、2、2、2，从中任取4张，可排出的四位数有________个. 【解析】 根据题意，分三种情况讨论： A4 ①取出的4张卡片有3张1、1张2，有 4 4个四位数； A3 3 A4 ②取出的4张卡片有3张1、1张2，有 4 4个四位数； A3 3 A4 ③取出的4张卡片有2张2、2张1，有 4 6个四位数. A2A2 2 2 综上所述，共有44614个四位数. 故答案为：14. 例9．将 这五个数字放在构成“W 型线段的 个端点位置，要求下面的两个数字分别比和 1,2,3,4,5, ” 5 它相邻的上面两个数字大,这样的安排方法种数为_______. 【解析】 由已知1和2必须在上面，5必须在下面， 分两大类来计算： （1）下面是3和5时，有2（1+1）＝4种情况； （2）下面是4和5时，有2A3 12种情况， 3 所以一共有4+12＝16种方法种数． 3故答案为16． 例10．某活动中，有42人排成6行7列，现从中选出3人进行礼仪表演，要求这3人中的任意2人不同行 也不同列，则不同的选法种数为 （用数字作答）． 【解析】 先按顺序依次选三人共有C1 C1 C1 ， 42 30 20 C1 C1 C1 再去掉顺序数： 42 30 20 4200. A3 3 故答案为：4200. 例11．一个房间的地面是由12个正方形所组成，如图所示.今想用长方形瓷砖铺满地面，已知每一块长方 形瓷砖可以覆盖两块相邻的正方形，即 或 ，则用6块瓷砖铺满房间地面的方法有_______ 种. 【解析】 （1）先贴如图这块瓷砖， 然后再贴剩下的部分，按如下分类： 5! 5个 ： 1 ， 5! 44! 3个 ，2个 ： 4， 3! 3! 1个 ，4个 ： 3， 2! （2）左侧两列如图贴砖， 然后贴剩下的部分： 3! 3个 ： 1， 3! 1个 ，2个 ：2!2， 综上，一共有1431211（种）. 故答案为：11. 例12．书架上某层有6本书，新买3本插进去，要保持原有6本书的顺序，有_____种不同的插法（具体数 字作答） 【解析】 原来的6本书，加上新买的3本书，随意排列共有A9种排法，原来的6本书随意排列共有A6种排法，而 9 6 A9 原来特有的顺序只有1种，所以共有 9 =987=504种方法. A6 6 故答案为：504. 例13．某地环保部门召集6家企业的负责人座谈，其中甲企业有2人到会，其余5家企业各有1人到会， 会上有3人发言，则发言的3人来自3家不同企业的可能情况的总数为_______． 5【解析】 （1）当发言的3人有来自甲企业，则共有：C1C2 20； 2 5 （2）当发言的3人没有来自甲企业，则共有：C3 10； 5 所以可能情况的总数为201030种. 例14．如图所示，某货场有三堆集装箱，每堆2个，现需要全部装运，每次只能从其中一堆取最上面的一 个集装箱，则在装运的过程中不同取法的种数是____________（用数字作答）. 【解析】 因为有六个集装箱，需要全部装运，共有A6 720种取法， 6 又因为每次只能从其中一堆取最上面的一个集装箱， A6 720 由排列中的定序问题，可知不同的取法有 6  90种. A2A2A2 8 2 2 2 故答案为：90. 例15．五个人并排站在一排，如果甲必须站在乙的右边(甲乙可不相邻)，则不同的排法有_______种. 【解析】 五个人并排站在一排，共有A5 120种， 5 其中甲、乙两人共有A2 2种顺序，各占一半， 2 A5 120 所以甲必须站在乙的右边(甲乙可不相邻)的不同的排法有 5  60种， A2 2 2 故答案为：60 例16．某工程队有6项工程需要先后单独完成，其中工程乙必须在工程甲完成后才能进行，工程丙必须在 工程乙完成后进行，又工程丁必须在丙完成后立即进行，那么安排这6项工程的不同的排法种数是____. 【解析】 因为工程丁必须在丙完成后立即进行，等价于丙丁看成一个元素，共五个元素进行排序，共有A5 120种， 5 其中3个元素共有A3 6种顺序， 3 6A5 120 所以安排这6项工程的不同的排法种数是 5  20种， A3 6 3 故答案为：20 例17．在班级活动中，4名男生和3名女生站成一排表演节目：（写出必要的数学式，结果用数字作答） （1）女生甲不能站在左端，女生乙不能站在右端，有多少种不同的排法？ （2）甲乙丙三人按高低从左到右有多少种不同的排法？（甲乙丙三位同学身高互不相等） （3）现在有7个座位连成一排，仅安排4个男生就坐，怡好有两个空座位相邻的不同坐法共有多少种？ 【解析】 （1）根据题意，分2种情况讨论： ①，女生甲站在右端，其余6人全排列，有A6 720种情况， 6 ②，女生甲不站在右端，甲有5种站法，女生乙有5种站法，将剩余的5人全排列，安排在剩余的位置， 有A5 120种站法， 5 则此时有551203000种站法， 则一共有A6 55A5 72030003720种站法； 6 5 （2）根据题意，首先把7名同学全排列，共有A7种结果， 7 甲乙丙三人内部的排列共有A3 6种结果， 3 A7 要使的甲乙丙三个人按照一个高矮顺序排列，结果数只占6种结果中的一种，则有 7 840种. A3 3 （3）根据题意，恰好有两个空座位相邻分2种情况：①两个相邻空座位在两边，12或67上，第三个空座 有4种选择；②两个相邻空座位在中间，可能是23，34，45，56中的一个，第三个空位有3种选择，4个 男生全排列有A4 24种坐法，共(2443)24480 种选派方法． 4 例18．（1）4本不同的书平均分成两堆，每堆两本，有几种分法？ （2）10人坐成一排，要求甲、乙、丙三人按从左到右的顺序就坐（不一定要相邻），有几种坐法？ 7