北京市海淀区2024届高三上学期期中考试数学(1)_2023年11月_01每日更新_05号_2024届北京市海淀区高三上学期期中考试

2023 北京海淀高三（上）期中 数 学 2023.11 本试卷共6页，150分，考试时长120分钟。考生务必将答案答在答题纸上，在试卷上作答无效。考试 结束后，将本试卷和答题纸一并交回. 第一部分(选择题共 40分) 一、选择题共10小题，每小题4分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。 (1)已知集合A=  x x2  ，B=1,2，则A B = (A) (−,2) (B) (−,2] (C) 1 (D) 1,2 2 (2)若复数z满足zi= ，则z= 1+i (A)−1−i (B) −1+i (C) 1−i (D) 1+i (3)下列函数中，既是偶函数又在区间(0,+) 上单调递增的是 (A) y =lnx (B)y = x3 (C)y = tanx (D)y =2x (4)已知向量a，b满足a =(2，1) ，a−b=(−1，2) ，则ab= (A)-5 (B)0 (C)5 (D)7 (5)设等差数列a 的前n项和为S ，且S =15，则a ·a 的最大值为 n n 5 2 4 9 (A) (B)3 4 (C)9 (D)36 3 (6)设a=log 6，b=log 3，c= ，则 4 2 2 (A)a bc (B)c ba (C)ba c (D)bc a (7)“sin+tan0”是“为第一或第三象限角”的 (A)充分而不必要条件 (B)必要而不充分条件 (C)充分必要条件 (D)既不充分也不必要条件 (8)在ABC中，sinB =sin2A，c =2a，则| 第1页/共4页(A)B为直角 (B) B为钝角 (C) C 为直角 (D) C 为钝角 (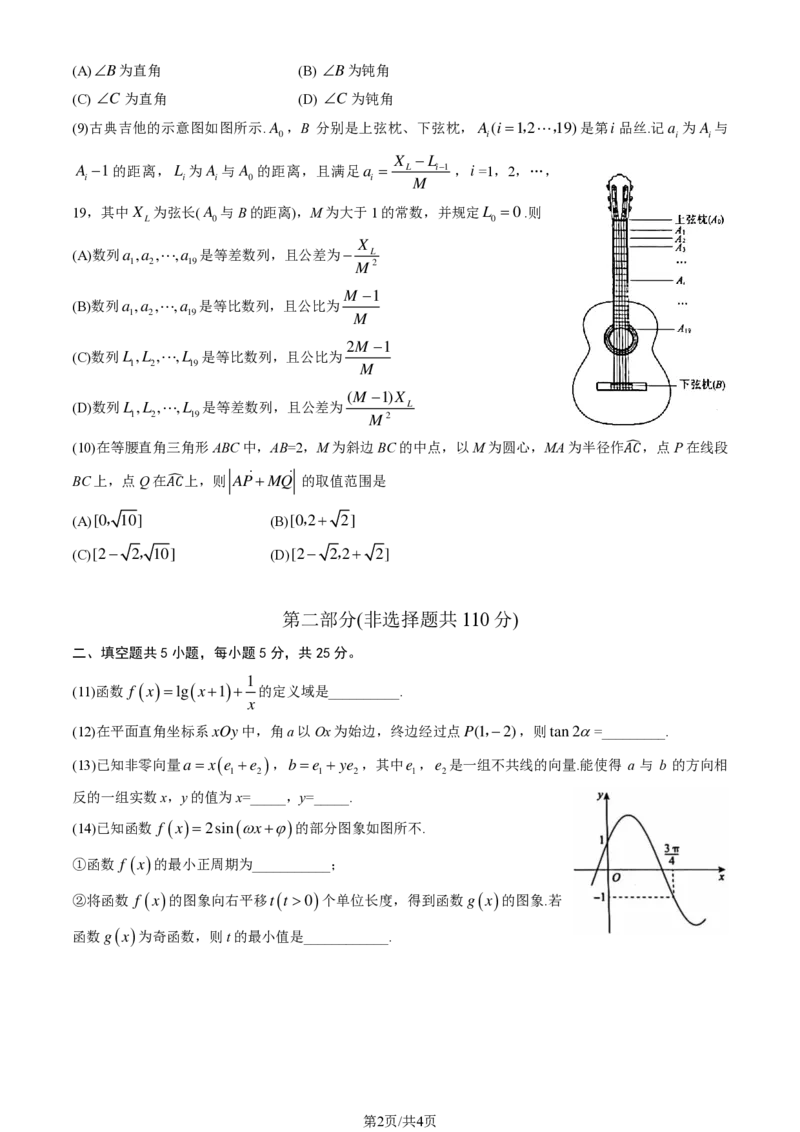9)古典吉他的示意图如图所示.A ，B 分别是上弦枕、下弦枕， A(i =1，2，19)是第i品丝.记 0 i 第2页/共4页 a i 为 A i 与 X −L A −1的距离，L 为 A 与 A 的距离，且满足a = L i−1 ，i =1，2，…， i i i 0 i M 19，其中X 为弦长(A 与B的距离)，M为大于1的常数，并规定L =0.则 L 0 0 X (A)数列a ,a ,,a 是等差数列，且公差为− L 1 2 19 M2 M −1 (B)数列a ,a ,,a 是等比数列，且公比为 1 2 19 M 2M −1 (C)数列L,L ,,L 是等比数列，且公比为 1 2 19 M (M −1)X (D)数列L,L ,,L 是等差数列，且公差为 L 1 2 19 M2 (10)在等腰直角三角形ABC中，AB=2，M为斜边BC的中点，以M为圆心，MA为半径作𝐴̂𝐶，点P在线段 BC上，点Q在𝐴̂𝐶上，则 AP+MQ 的取值范围是 (A)[0，10] (B)[0，2+ 2] (C)[2− 2，10] (D)[2− 2，2+ 2] 第二部分(非选择题共 110分) 二、填空题共5小题，每小题5分，共25分。 1 (11)函数 f (x)=lg(x+1)+ 的定义域是__________. x (12)在平面直角坐标系xOy中，角a以Ox为始边，终边经过点P(1，−2)，则tan2=_________. (13)已知非零向量a = x(e +e )，b=e + ye ，其中e ，e 是一组不共线的向量.能使得 a 与 b 的方向相 1 2 1 2 1 2 反的一组实数x，y的值为x=_____，y=_____. (14)已知函数 f (x)=2sin(x+)的部分图象如图所不. ①函数 f (x)的最小正周期为___________； ②将函数 f (x)的图象向右平移t(t 0)个单位长度，得到函数g(x)的图象.若 函数g(x)为奇函数，则t的最小值是____________.2x +a,xa, (15)已知函数 f (x)= 给出下列四个结论: x2 +2ax,xa. ①当a=0时， f (x)的最小值为0； 1 ②当a 时， f (x)存在最小值; 3 ③记 f (x)的零点个数为g(a)，则函数g(a)的值域为{0，1，2，3}; x +x ④当a1时，对任意x ,x R， f(x )+ f (x )2f( 1 2) 1 2 1 2 2 其中所有正确结论的序号是____________. 三、解答题共6小题，共85分。解答应写出文宇说明，演算步骤或证明过程。 (16)(本小题14分) 已知无穷等比数列a 的各项均为整数，其前n项和为S ，a =3，a +a =10. n n 2 1 3 (I)求a 的通项公式； n (II)证明：对kN*,3S ,2S ,S 这三个数成等差数列. k k+1 k+2 (17)(本小题14分)  已知函数 f(x)=2cosxcos(x+)( )，从条件①、条件②、条件③这三个条件中选择一个作为已 2 知，使函数 f (x)存在. (I)求的值；  (II)求 f (x)在区间［− ,0］上的最大值和最小值. 2  条件①: f( )=1； 3  条件②：函数 f (x)在区间[0, ]上是增函数； 4 2 条件③：xR, f(x) f( ) 3 注：如果选择的条件不符合要求，得0分；如果选择多个符合要求的条件分别解答，按第一个解答计分. (18)(本小题14分) 已知曲线C: y =4−x2与x轴交于不同的两点A，B(点A在点B的左侧)，点P(t，0)在线段AB上(不与端点 重合)，过点P作x轴的垂线交曲线C于点Q. (I)若APQ为等腰直角三角形，求APQ的面积； (D)记APQ的面积为S(t)，求S(t)的最大值. 第3页/共4页(19)(本小题14分) 某景区有一人工湖，湖面有A，B两点，湖边架有直线型栈道CD，长为50m，如图所示.现要测量A，B两 点之间的距离，工作人员分别在 C，D两点进行测量，在 C 点测得ACD =45，BCD =30;在 D点 测得ADB =135，BDC =120.(A，B，C，D在同一平面内) (I)求A，B两点之间的距离； (n)判断直线CD与直线AB是否垂直，并说明理由. (20)(本小题14分) x +a 1 2 已知函数 f (x)= ，且 f (1)= ， f (4)= x2 +b 4 19 (I)求a，b的值； (II)求 f (x)的单调区间； (III)设实数 m 满足：存在 kR ，使直线 y =kx+m 是曲线 y = f (x) 的切线，且 kx+m f (x)对 x[0,+)恒成立，求m的最大值. (21)(本小题15分) 设无穷数列a 的前 n 项和为S ，i 为单调递增的无穷正整数数列，记A =S −S (n=1，2，)，定 n n n n i i n+1 n   义= jN* S −S 0,k = j+1, j+2, . k j (I)若a =n，i =n2(n=1，2，)，写出A，A 的值； n n 1 2 1 (II)若a =(− )n−1(n=1，2，)，求Ω; n 2 1,x0,  (III)设sgn(x)=0,x=0, 求证：对任意的无穷数列a ，存在数列i ，使得sgn(A )为常数列. n n n  −1,x0.  第4页/共4页海淀区 2023—2024 学年第一学期期中练习 高三数学参考答案 一、选择题（共10小题，每小题4分，共40分） （1）B （2）A （3）D （4）C （5）C （6）D （7）C （8）C （9）B （10）A 二、填空题（共5小题，每小题5分，共25分） 4 （ 11 ）(1,0) (0,) （12） 3 3 π （13）1 1（答案不唯一） （14） π 2 8 （15）①③ 三、解答题（共6小题，共85分） （16）（共14分） 解：（Ⅰ）设等比数列{a }的公比为q. n 因为a 3，a a 10， 2 1 3 所以a q3，a a q2 10． 1 1 1  1 q3, q , 所以 或 3 a 1 1,  a 1 9. 因为a 均为整数， n q3, 所以 a 1 1. 所以a 3n1 (n1,2,3, )． n 3n 1 （Ⅱ）由（Ⅰ）知，S  (n1,2,3, )． n 2 3k11 3k 1 13k1 所以2S 3S 2 3  ， k1 k 2 2 2 3k2 1 3k11 13k1 S 2S  2  ． k2 k1 2 2 2 高三年级（数学）参考答案 第 1 页（共 7 页）13k1 所以2S 3S S 2S  . k1 k k2 k1 2 13k1 所以3S ，2S ，S 是以 为公差的等差数列． k k1 k2 2 （17）（共14分） π 解：选择条件①： f( )1. 3 （Ⅰ）因为 f(x)2cosxcos(x)， π π π 所以2cos cos( )1，即cos( )1. 3 3 3 π 所以2kπ (kZ). 3  π 因为|| ，所以 ． 2 3 π （Ⅱ）由（Ⅰ）可得： f(x)2cosxcos(x ) 3 1 3 2cosx( cosx sinx) 2 2 1 3  2cos2x sin2x 2 2 1 3 1  cos2x sin2x 2 2 2 π 1 cos(2x ) . 3 2 π 4π π π 因为x[ ,0]，所以 ≤2x ≤ ． 2 3 3 3 π π π 所以当2x π，即x 时，cos(2x )取得最小值1. 3 3 3 π 1 所以 f(x)在区间[ ,0]上的最小值是 ； 2 2 π π π 1 当2x  ，即x0时，cos(2x )取得最大值 ． 3 3 3 2 π 所以 f(x)在区间[ ,0]上的最大值是1． 2 高三年级（数学）参考答案 第 2 页（共 7 页）2π 选择条件③：xR， f(x) f( ). 3 （Ⅰ）由题意得： f(x)2cosxcos(x) 2cosx(cosxcossinxsin) 2cos2xcossin2xsin cos2xcossin2xsincos cos(2x)cos. 2π 因为xR， f(x) f( )， 3 2π 4π 所以 f(x)的最小值为 f( )，即cos( )1. 3 3 4π π 所以(2k1)π 2kπ (kZ). 3 3  π 因为|| ，所以 ． 2 3 （Ⅱ）同选择条件①的（Ⅱ）. （18）（共12分） 解：（Ⅰ）由题意令4x2 0得x2．所以A(2,0)，B(2,0). 因为点P(t,0)在线段AB上（不与端点重合）， 所以2t2. 因为△APQ为等腰直角三角形， 所以|PQ||AP|. 由题意可知点Q在x轴上方， 所以Q(t,t2)． 因为点Q在曲线C上， 所以t24t2. 所以t 2（舍），t 1，即Q(1,3). 1 2 1 1 9 所以△APQ的面积为 |AP||PQ| 33 ． 2 2 2 高三年级（数学）参考答案 第 3 页（共 7 页）（Ⅱ）由题意可知Q(t,4t2)，2t2. 1 1 所以S(t) (t2)(4t2) (t3 2t2 4t8)． 2 2 1 所以S'(t) (3t2 4t4). 2 2 令3t2 4t40，得t 2，t  ． 1 2 3 S(t)与S'(t)在区间(2,2)上的情况如下： 2 2 2 t (2, ) ( ,2) 3 3 3 S'(t)  0  S(t) ↗ 极大值 ↘ 2 128 因为S( ) ， 3 27 2 128 所以当t 时，S(t)取得最大值 ． 3 27 （19）（共13分） 解：（Ⅰ）连接AB.因为ADB135，BDC 120， 所以ADC 105． 因为ACD45， 所以CAD30. CD AD 在△ACD中，  ． sinCAD sinACD 所以AD 2CD． 因为BCD30， 所以DBC30． 所以BDCD. 在△ABD中，AB2 AD2BD22ADBDcos135 5CD2. 因为CD50， 高三年级（数学）参考答案 第 4 页（共 7 页）所以AB 5CD50 5 ，即A，B两点之间的距离为50 5m . （Ⅱ）CD与AB不垂直．理由如下： E B 延长CD交AB于点E. A AB AD 在△ABD中，  . D sinADB sinABD 5 1 所以sinABD  . 5 2 因为0ABD90， C 所以ABD30. 所以BEC180CBEBCD90. 所以直线CD与直线AB不垂直． （20）（共14分） 1 2 解：（Ⅰ）因为 f(1) ， f(4) ， 4 19 a1 1  ,  b1 4 a0, 所以 解得  a2  2 , b3. b16 19 x （Ⅱ）由（Ⅰ）得 f(x) ． x2 3 1 (x2 3) x2x 2 x 所以 f '(x) (x2 3)2 3(1x2)  . 2 x(x2 3)2 令 f '(x)0，得x1． 当x(0,1)时， f '(x)0；当x(1,)时， f '(x)0. 所以 f(x)的单调递增区间是(0,1)；单调递减区间是(1,). 1 （Ⅲ）由（Ⅱ）可知当x1时， f(x)取得最大值 . 4 1 1 1 1 ①当m 时，存在直线y 是曲线y f(x)在点(1, )处的切线，且 f(x) 4 4 4 4 高三年级（数学）参考答案 第 5 页（共 7 页）对x[0,)恒成立，符合题意． 1 ②当m 时，设直线ykxm为曲线y f(x)的切线，切点为(x , y )，则 4 0 0 x 0,  0  1 y  .   0 4 y m 所以k  0 0． x 0 m 取x  ，则x 0. 1 k 1 x 因为 f(x ) 1 0，kx m0， 1 x2 3 1 1 所以kx m f(x )，即存在x (0,)，kx m f(x )，不符合题意. 1 1 1 1 1 1 综上可知，m 的最大值是 ． 4 （21）（共15分） 解：（Ⅰ）A 9,A 35． 1 2 2 2 1 （Ⅱ）由题意知S   ( )n. n 3 3 2 1 ①若 j为奇数，则S S a ( )j 0. j1 j j1 2 所以 j． ②若 j为偶数，则当k j1,j2, 时， 2 1 1 2 1 1 S S  [( )j ( )k] [( )j ( )k]0. k j 3 2 2 3 2 2 所以 j． 所以 {x|x2m,m1,2, }. （Ⅲ）（1）若为有限集，设其最大元素为m （若为空集，取m0），则当 jm1,m2, 时，存在k j满足S S 0. k j 令 i m1 ， i min{kN*|ki ,S S 0} （ n1,2, ）， 则 1 n1 n k i n 高三年级（数学）参考答案 第 6 页（共 7 页）A S S 0. 所以 sgn(A )1（n1,2, ）； n i i n n1 n （2）若为无限集，设{j , j , }，其中 j  j  ，记B S S ， 1 2 1 2 n j j n1 n 则B 0（n1,2, ）. n ①若数列{B }中只有有限项为正数，记mmax{nN*|B 0}（若 n n 高三年级（数学）参考答案 第 7 页（共 7 页） { B n } 中没 有正数项，取m0），则B 0（n1,2, ）． mn 令i  j （n1,2, ），则A S S B 0（n1,2, ）. n mn n i i mn n1 n 所以 sgn(A )0（n1,2, ）； n ②若数列{B } 中有无穷项为正数，将这些项依次记为 B ,B , ，其中 n t t 1 2 t t  ，则B S S 0（n1,2, ）. 1 2 t j j n tn1 tn 令i  j （n1,2, ），则A S S B +B + +B =B 0. n t n j j t t +1 t 1 t n tn+1 tn n n n+1 n 所以 sgn(A )1（n1,2, ）. n 综上所述，对任意的无穷数列a 都存在数列i ，使得{sgn(A )}为常数列. n n n