文档内容
吉林省八校联考 2024-2025 学年高二上学期 1 月期末考试数学试题
考生注意:
1.本试卷满分150分,考试时间120分钟.
2.答卷前考生务必将自己的姓名,准考证号填写在答题卡上.
3.答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑.如需改动,用
橡皮擦干净后再选涂其他答案标号.答非选择题时,将答案写在答题卡上.写在本试卷上无效.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 直线 的倾斜角是( )
A. B. C. D.
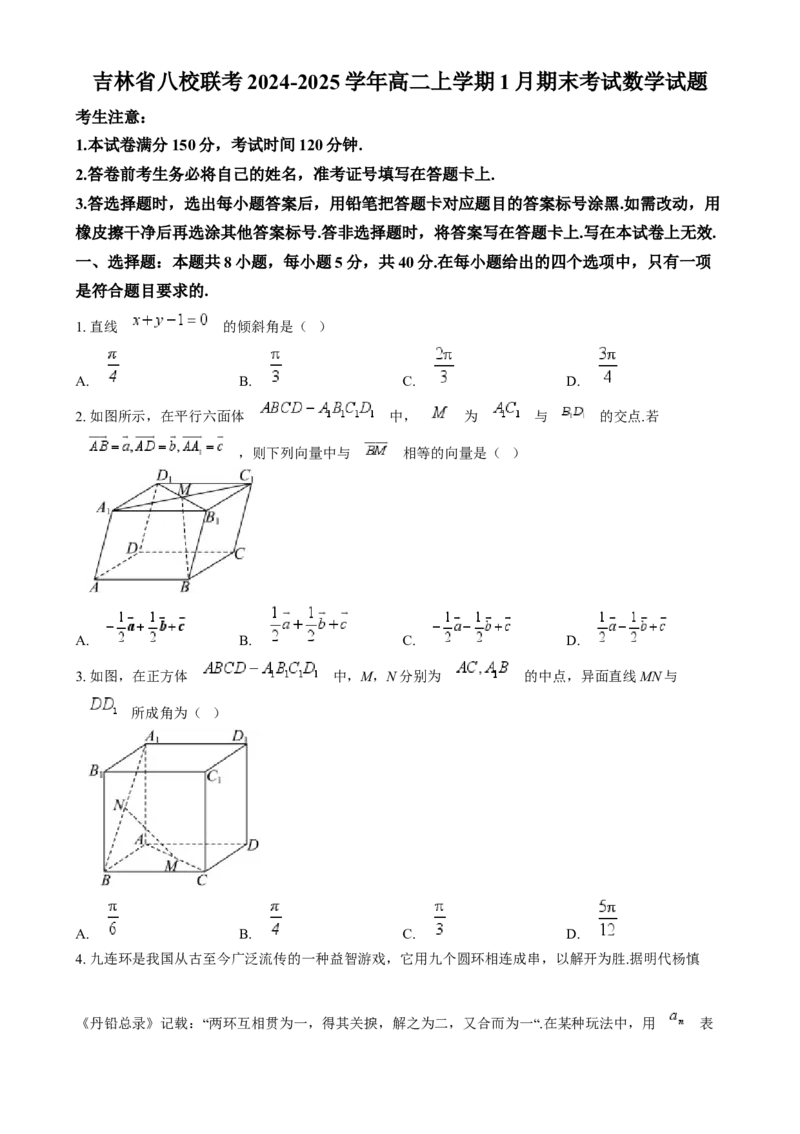
2. 如图所示,在平行六面体 中, 为 与 的交点.若
,则下列向量中与 相等的向量是( )
A. B. C. D.
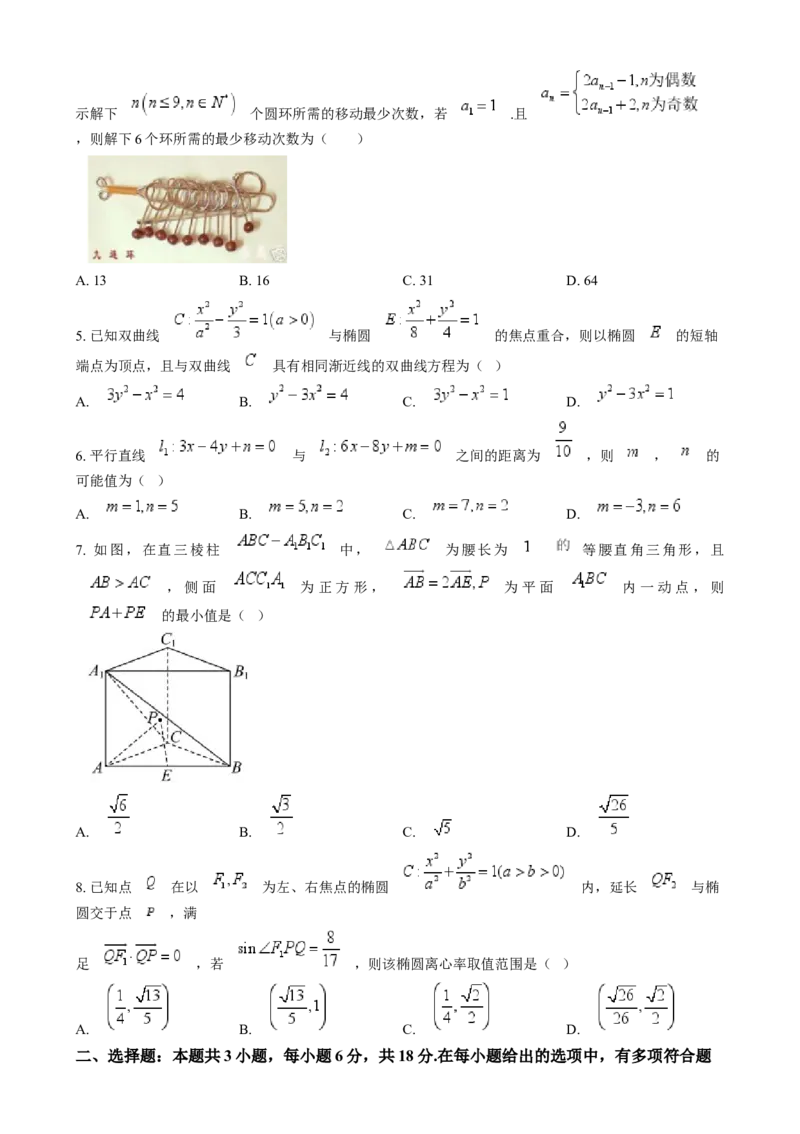
3. 如图,在正方体 中,M,N分别为 的中点,异面直线MN与
所成角为( )
A. B. C. D.
4. 九连环是我国从古至今广泛流传的一种益智游戏,它用九个圆环相连成串,以解开为胜.据明代杨慎
《丹铅总录》记载:“两环互相贯为一,得其关捩,解之为二,又合而为一“.在某种玩法中,用 表示解下 个圆环所需的移动最少次数,若 .且
,则解下6个环所需的最少移动次数为( )
A. 13 B. 16 C. 31 D. 64
5. 已知双曲线 与椭圆 的焦点重合,则以椭圆 的短轴
端点为顶点,且与双曲线 具有相同渐近线的双曲线方程为( )
A. B. C. D.
6. 平行直线 与 之间的距离为 ,则 , 的
可能值为( )
A. B. C. D.
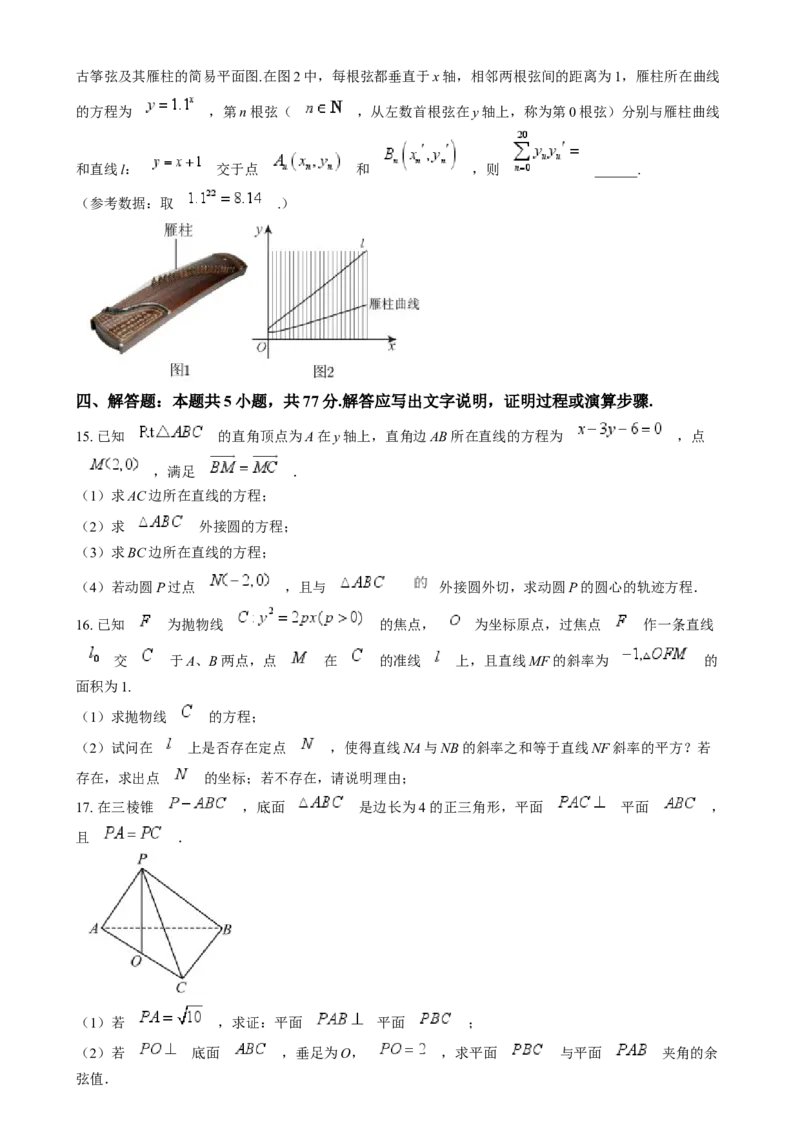
7. 如图,在直三棱柱 中, 为腰长为 等腰直角三角形,且
,侧面 为正方形, 为平面 内一动点,则
的最小值是( )
A. B. C. D.
8. 已知点 在以 为左、右焦点的椭圆 内,延长 与椭
圆交于点 ,满
足 ,若 ,则该椭圆离心率取值范围是( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知椭圆 上一点 , 、 分别为左、右焦点, ,
的面积为 ,则下列选项正确的是( )
A. 若 ,则
B. 若 ,则满足题意 点 有四个
C. 椭圆 内接矩形周长的最大值为
D. 若 为钝角三角形,则
10. 如图,一个结晶体的形状为平行六面体 ,其中,以顶点 为端点的三条棱
长均为6,且它们彼此的夹角都是 ,则下列说法中正确的是( )
A. B.
C. 向量 与 的夹角是 D. 与AC所成角的余弦值为
11. 在数列 中, ,则以下结论正确的为(
)
A. 数列 为等差数列
B.
C. 当 取最大值时, 的值为51
D. 当数列 的前 项和取得最大值时, 的值为49或51
三、填空题:本题共3小题,每小题5分,共15分.
12. 圆 和圆 的公切线条数为
__________.
13. 已知 ,直线 ,且 ,则
的最小值为__________.
14. 如图1所示,古筝有多根弦,每根弦下有一个雁柱,雁柱用于调整音高和音质.图2是根据图1绘制的古筝弦及其雁柱的简易平面图.在图2中,每根弦都垂直于x轴,相邻两根弦间的距离为1,雁柱所在曲线
的方程为 ,第n根弦( ,从左数首根弦在y轴上,称为第0根弦)分别与雁柱曲线
和直线l: 交于点 和 ,则 ______.
(参考数据:取 .)
四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15. 已知 的直角顶点为A在y轴上,直角边AB所在直线的方程为 ,点
,满足 .
(1)求AC边所在直线的方程;
(2)求 外接圆的方程;
(3)求BC边所在直线的方程;
(4)若动圆P过点 ,且与 外接圆外切,求动圆P的圆心的轨迹方程.
16. 已知 为抛物线 的焦点, 为坐标原点,过焦点 作一条直线
交 于A、B两点,点 在 的准线 上,且直线MF的斜率为 的
面积为1.
(1)求抛物线 的方程;
(2)试问在 上是否存在定点 ,使得直线NA与NB的斜率之和等于直线NF斜率的平方?若
存在,求出点 的坐标;若不存在,请说明理由;
17. 在三棱锥 ,底面 是边长为4的正三角形,平面 平面 ,
且 .
(1)若 ,求证:平面 平面 ;
(2)若 底面 ,垂足为O, ,求平面 与平面 夹角的余
弦值.18 已知等差数列 满足 ,等比数列 满足
.
(1)求数列 的通项公式;
(2)令 ,求证: ,其中 .
19. 已知椭圆 ,左顶点分别为 ,上顶点为 ,左右焦点分别为
为椭圆上一点, 最大值为 的面积为 .
(1)求椭圆方程;
(2)已知直线过 与椭圆 交与M,N两点( 在 上方),且 ,
若 ,求直线斜率 值范围.